基于Gabor滤波器族的地震图像增强算法

刘天时，杨 雪，李湘眷

（西安石油大学 计算机学院，陕西 西安710065）

0 引 言

地震资料的构造解释不同于油气检测和地层解释，它需要真振幅和宽频带的地震数据。同相轴连续和横向分辨率良好的地震数据更有利于构造解释和计算机解释软件的自动解释。含大量噪声的地震数据会导致由地震数据形成的地震图像信噪比降低，这严重影响地震剖面图像的进一步解析。文献 ［1］中结合改进的加权中值滤波和增强Lee滤波对SAR 图像的斑点噪声进行去噪，在有效去除SAR图像中斑点噪声的同时保持了图像的边缘信息；文献 ［2］针对图像的均匀噪声提出了一种基于小波变换的去噪方法，去噪效果好；文献 ［3］中将改进的Teager能量算子和Gabor函数结合用于指纹图像增强，对低质量指纹图像去噪和边缘增强效果较好；文献 ［4］在对图像进行小波变换后使用Curvelet变换进行图像去噪；文献 ［5］对传统小波分析的硬阈值、软阈值进行了改进，构造了一种阈值函数，对语音信号去噪效果良好。

传统的图像增强算法在增强对比度的同时增强了图像的噪声，因此图像去噪在图像预处理中占有重要地位。然而很多去噪算法只适用于特定的图像［6－8］，将其用于处理具有明显方向性的地震剖面图像时去噪效果不明显，从而使地震剖面图像的增强效果也受到一定程度的影响。因此，为了更好的对地震剖面图像进行增强处理，本文在已有图像增强算法的基础上，提出了一种融合小波变换和Gabor滤波器族的地震剖面图像增强算法，最后得到纹线更加突出、整体对比度增强的地震剖面图像。

1 小波变换和Gabor滤波

1.1 小波变换

在应用领域，特别是在信号处理、图像处理、语音处理以及众多非线性科学领域，小波变换被认为是继Fourier分析之后的又一个有效的时频分析方法，其可以用来表示信号的时间－频率特性［9］。小波变换更适用于考虑图像方向性的图像增强处理中［10］，因此将小波变换应用于地震剖面图像处理中，可以有效地对地震剖面图像起到增强作用，对地震剖面图像的进一步处理与研究起到良好的铺垫作用。

经过小波变换，原始地震剖面图像被分解为低频分量图和高频分量图。一般地，图像的主要信息对应于小波变换后的低频分量，图像的边缘和噪声对应于小波变换后的高频分量。根据实际需要，选择性的增强低频分量和削弱高频分量来实现图像增强。

1.2 Gabor滤波器

Gabor滤波器属于加窗傅立叶变换滤波器［11］。Gabor滤波器是自相似的，所有的Gabor滤波器都可以从一个母小波经过膨胀和旋转产生。Gabor滤波器的频率和方向表示接近人类视觉系统对于频率和方向的表示，并且常被用于纹理表示和描述。二维Gabor滤波器可以看作是一个对方向和尺度敏感的有方向性的显微镜。在空域，一个二维的Gabor滤波器是一个正弦平面波和高斯核函数的乘积。在实际应用中，Gabor滤波器可以提取频域中不同尺度、不同方向的相关特征。Gabor滤波器可以通过调节参数生成多种滤波器模版［12］，因此Gabor滤波器可以广泛的应用于不同图像的去噪处理中。

2 融合小波变换与Gabor滤波的地震图像增强

地震图像在预处理过程中往往受多方面因素制约，有时无法满足对图像处理的需求。传统的图像去噪算法容易在去除噪声的同时模糊图像的细节信息，因此找到平衡去除噪声与保留细节之间的算法显的尤为重要。下面先对地震剖面图像进行小波分解，提取高频分量图与低频分量图，根据地震剖面图像的纹理特征构造Gabor滤波器族，然后将高频分量的系数设置为零并使用Gabor滤波器族对低频分量图进行滤波去噪，最后重构图像得到增强后的地震剖面图像，如图1所示。

2.1 Gabor滤波器族设计

地震同相轴表现为线条结构，裂缝等地质体的分布在局部较小范围内可以看成是一致的，并且具有良好的频率特性和方向特性，因此需要选择适合地震剖面纹理特征的滤波算法。

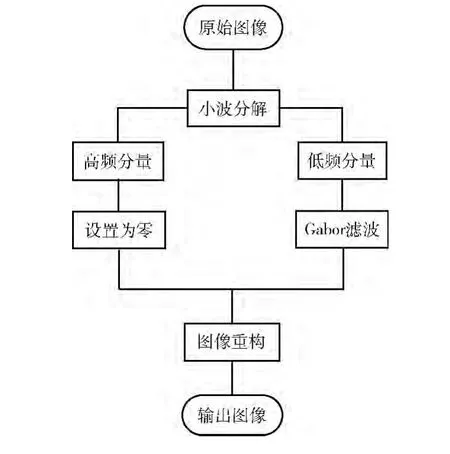
图1 融合小波变换与Gabor滤波的图像增强

Gabor滤波器族可以根据图像增强不同的需求来选择方向和频率，因此Gabor滤波器族更适用于具有明显方向性的地震剖面图像去噪中。使用Gabor滤波器可以在有效去除地震剖面纹线上噪声的同时不破坏其本身的纹线结构。文中取Gabor滤波算子的实数部分作为滤波模版，将近似余弦波的频率作为滤波器的频率建立滤波器族，得到的滤波结果基本不改变地震剖面图像本身的特征。

定义1 设wavelength为所构造滤波器的大小，θ为滤波器的方向，将Gabor滤波器分为奇滤波器和偶滤波器，分别定义如下

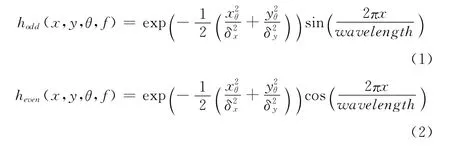
其中，xθ与yθ为

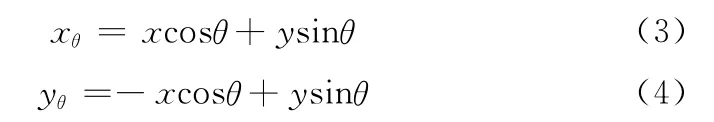
定义2 设u，v 表示尺度和方向，Wg表示滤波窗口大小，G（i，j）表示原始低频分量图，G′（i，j）表示滤波后的低频分量图，提取Gabor滤波器的实数部分对图像进行滤波，定义如下

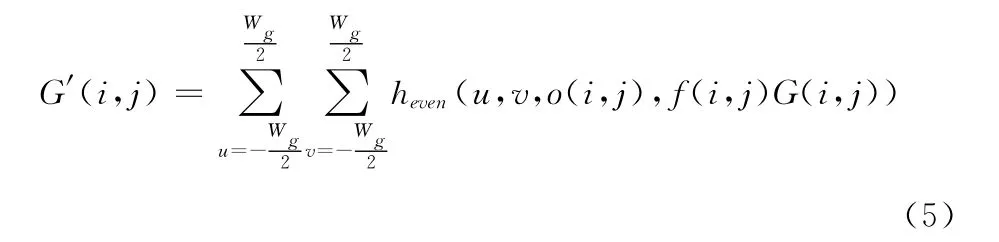
2.2 地震图像增强算法

改进的图像增强算法更适用于地震剖面图像增强。该算法提取小波分解后的低频分量图并使用Gabor滤波器族对其进行滤波去噪，最终重构图像得到纹线明显增强的地震剖面图像。具体的算法步骤如下：

步骤1 对原始地震剖面图像进行单层二维离散小波分解，提取高频分量图和低频分量图；

步骤2 将高频分量图的小波系数置零；

步骤3 通过式 （1）～式 （4）式构造Gabor奇滤波器和Gabor偶滤波器族；

步骤4 利用式（2）提取滤波器族实数部分，并采用式（5）对低频分量图进行滤波，获取去噪后的低频分量图；

步骤5 对步骤2中小波系数置零后的高频分量图和步骤4中滤波去噪后的低频分量图进行重构，得到增强后的地震剖面图像。

步骤1中，由于仅对低频分量图进行滤波去噪，因此只需要进行一次小波分解即可，提高了整体运算速率。步骤3中，经过反复实验，最终选取5个尺度，8个方向构造含有40个滤波器的滤波器族，滤波器族的方向变化由式（3）和式 （4）实现。实验表明，5个尺度、8 个方向的滤波器族滤波效果最好。由于本文算法针对图像增强，因此步骤4中提取Gabor滤波器族的实数部分与低频分量图进行卷积，实现低频分量图的滤波去噪。

3 仿真结果及分析

3.1 原始图像小波分解

传统图像增强算法在图像增强的同时模糊了图像中原有的边缘和细节信息。而小波分析具有基于多分辨率提取信号的特性，并且能够较为明显的区分噪声和信号，因此利用小波分析对地震剖面图像处理的结果更加精确。本文选取一幅地震剖面图像，如图2 （a）所示。在对原始地震剖面图像进行二维小波分解后，得到原始图像的低频分量图 （cA）和高频分量图。高频分量图又分为水平高频分量图cH，垂直高频分量图cV，对角高频分量图cD，如图2所示。低频分量图包含原始图像的主要信息，高频分量图包含原始图像的边缘信息及噪声。

图2 原始图像及小波分解图像

从图2 （a）中可以看出原始地震剖面图像具有明显的断裂、分叉等特征，纹理特征也不清楚，这不利于地震剖面图像的进一步解析。经过小波分解后，原始图像的主要信息分布在图2 （a）中，噪声主要分布在图2 （c）、图2（d）、图2 （e）中。

3.2 低频分量图去噪

采用Gabor滤波器不但能够去除噪声，并且能把地震剖面的纹线结构不失真地保留下来。通常采用多个方向、多个尺度的Gabor滤波器族来进行滤波去噪。本文将Gabor滤波器的实现分为奇滤波器和偶滤波器。其中，奇滤波器代表实部，偶滤波器代表虚部，用实部滤波可以进行图像平滑，用虚部滤波可以进行图像边缘检测。由于本文是对图像增强算法的研究，因此提取Gabor滤波器的实部对低频分量图进行滤波去噪。

利用5个尺度，8个方向组成的滤波器族的实部与低频分量图进行卷积，得到不同尺度、不同方向的Gabor滤波结果，并将所得结果加权平均，构造出去噪后的低频分量图。为了方便分析Gabor滤波结果，图3描述了低频分量图两个尺度4个方向的Gabor滤波结果，每个尺度均有4个方向，分别为0°，45°，90°，135°，分别表示了低频分量图不同方向的纹理特征。

图3 Gabor滤波结果

3.3 图像增强

经过MATLAB仿真实验，本文算法将小波变换与Gabor滤波结合应用于地震剖面图像的增强处理，能够较好地避免传统算法中产生虚假纹线的现象，达到一致性的增强。利用Gabor滤波器族的多尺度多方向特性使低频分量图滤波去噪效果良好，重构后的地震剖面图像纹线得到明显增强，整体对比度在一定程度上得到了提高。Gabor滤波器族的参数是通过实验法得到的。实验法是基于固定参数的情况下，通过具体实验比较其性能，最后选择最合适的参数［13］。本文用kx，ky 控制Gabor滤波器族的窗口大小进行滤波，其中，kx 控制滤波器的频带宽度，ky 控制滤波器的方向。kx，ky 由人为给出，通过反复实验，kx，ky 取值从0.5开始时，图像增强效果较明显。如果kx，ky 取值太小，则图像增强效果不明显；如果kx，ky 取值太大，则图像的细节和边缘信息会被平滑掉。

由图4可以看出，当kx＝0.95，ky＝0.95时，地震剖面图像增强效果最明显。当kx，ky 小于0.95 时，地震剖面图像增强效果不明显；当kx，ky 大于0.95 时，在去噪的同时模糊了原始地震剖面图像的细节和边缘信息。

图4 不同参数增强效果比较

小波变换是地震信号等非平稳信号分析的有力工具，Gabor滤波器族具有良好的频率特性和方向特性，能够保证地震剖面图像的真实性。因此，结合小波变换与Gabor滤波器族各自的优点使图像增强效果更加明显。实验结果表明，使用本文算法对地震剖面图像进行去噪，去噪的同时有效保留了图像的纹理和边缘信息，最终得到纹线清晰，整体对比度增强的地震剖面图像。

3.4 结果分析

对图像增强效果进行评价的方法分为主观评价与客观评价。本文选取均方误差MSE （mean squared error）和PSNR（peak signal to noise ratio）作为主要的客观评价标准

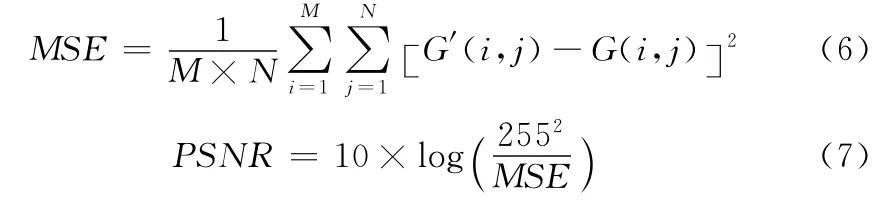
式中：M 和N 为图像尺寸，G（i，j）为原始图像，G′（i，j）为处理后的图像。均方误差越小，峰值信噪比越大，增强后的图像与原图像的差异越大，一定程度上可以表明图像被增强的程度越大。表1列出了不同增强算法得到的地震剖面图像的均方误差MSE和峰值信噪比PSNR。

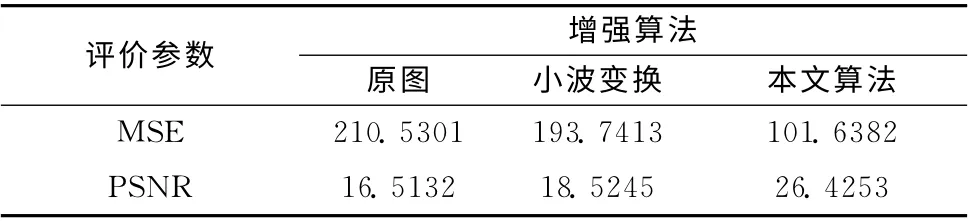
表1 图像增强算法评价参数比较

从表1可以看出，经与原始图像和小波变换增强后的图像比较，本文算法处理后的图像均方误差最小，峰值信噪比最大，表明针对地震剖面图像增强，本文算法增强效果较为明显。

另外，图5 （c）显示了利用本文算法进行图像增强的结果，比直接对地震剖面图像使用小波变换增强的视觉效果更好，同时地震剖面图像的纹理特征得到较好的保留。因此，不论是从客观图像质量评价标准还是从主观图像质量评价标准来看，本文所提出的算法都是一种有效的地震剖面图像增强算法。

图5 不同算法增强效果比较

4 结束语

本文对传统的图像增强算法进行了改进，根据地震剖面图像纹线的方向性，设计并使用Gabor滤波器族对低频分量图滤波去噪，有针对性的进行了地震剖面图像增强。使用Gabor滤波器族对小波分解后的低频分量图滤波去噪，不仅减少了计算量，使运算速率提高，而且由于图像的大部分信息主要体现在低频分量图中，因此仅对低频分量图进行滤波结果更加精确。本文算法适用于地震剖面图像增强，效率更高、效果更好，对地震资料的进一步解释处理有一定地促进作用。将Gabor滤波器族用于地震剖面图像增强时，其参数的确定及优化仍有待进一步改进，如何根据地震资料处理的需求更加高效、准确的对地震剖面图像进行增强，还有待进一步研究。

［1］HAN Mingxing，ZHENG Yongguo.Research on SAR image speckle noise filtering methods［J］.Computer Applications and Software，2012，29 （8）：257－258 （in Chinese）. ［韩明星，郑永果.SAR 图像斑点噪声的滤波方法研究 ［J］.计算机应用与软件，2012，29 （8）：257－258.］

［2］Yan R，Shao L，Liu Y.Nonlocal hierachical dictionary learning using wavelets for image denoising ［J］.IEEE Transactions Image Processing，2013，22 （12）：4689－4698.

［3］WANG Lei，ZHENG Jianwei，WANG Wanliang.Fingerprint image enhancement based on wavelet transform and Teager energy operator ［J］.Computer Applications and Software，2010，27 （8）：59－61 （in Chinese）.［王磊，郑建炜，王万良.基于小波变换和Teager能量算子指纹图像增强 ［J］.计算机应用与软件，2010，27 （8）：59－61.］

［4］WANG Biao，LI Jianwen，WANG Zhongfei.Threshold denoising method based on wavelet analysis［J］.Computer Engineering and Design，2011，32 （3）：1099－1102 （in Chinese）.［王彪，李建文，王钟斐.基于小波分析的新阈值去噪方法［J］.计算机工程与设计，2011，32 （3）：1099－1102.］

［5］Yi Qiaoling，Weng Yu，He Jiayong.Image denoise based on Curvelet transform ［C］／／IEEE Workshop on Electronics，Computer and Applications，2014：412－414.

［6］LU Yujing，LI Haiyan，FEI Qinshui，et al.Noise and speckle reduction of ultrasonic images using an improved Rayleightrimmed bilateral filtering algorithm ［J］.Computer Engineering and Design，2014，35 （1）：228－232 （in Chinese）.［陆玉婧，李海燕，费勤水，等.瑞利微调双边滤波超声图像降噪去斑算法 ［J］.计算机工程与设计，2014，35 （1）：228－232.］

［7］YANG Xianfeng，FAN Yong，PENG Bo，et al.Fast denoising algorithm based on regions for image corrupted by Gaussian noise［J］.Computer Engineering and Design，2014，35 （4）：1341－1346 （in Chinese）.［杨先凤，樊勇，彭博，等.去除高斯噪声的快速分区域去噪算法 ［J］.计算机工程与设计，2014，35 （4）：1341－1346.］

［8］QIAO Ziliang，DU Huimi.NL＿MEANS algorithm based on K－means clustering for ultrasound image denoising ［J］.Computer Engineering ＆Design，2014，35 （3）：939－942 （in Chinese）.［乔子良，杜慧敏.基于K 均值聚类NL－MEANS 算法的超声图像去噪 ［J］.计算机工程与设计，2014，35 （3）：939－942.］

［9］Jijiang H，Jianzhong C，Bo Y，et al.Low－memory－usage and high－speed image wavelet transform ［C］／／4th IEEE International Conference on Information Science and Technology，2014：523－526.

［10］Bhatnagar G，Wu QMJ，Raman B.A new fractional random wavelet transform for fingerprint security ［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A：Systems and Humans，2012，42 （1）：262－275.

［11］Deshmukh A，Pawar S，Joshi M.Feature level fusion of face and fingerprint modalities using Gabor filter bank ［C］／／IEEE International Conference on Signal Processing，Computing and Control，2013：1－5.

［12］Garg B，Chaudhary A，Mendiratta K，et al.Fingerprint recognition using Gabor filter ［C］／／nternational Conference on Computing for Sustainable Global Development.IEEE，2014：953－958.

［13］ZHAO Yingnan，YANG Jingyu，MENG Xianquan.A practical design for parameters of Gabor filters［J］.Computer Engineering，2006，32 （19）：173－175 （in Chinese）.［赵英男，杨静宇，孟宪权.一种实用的Gabor滤波器族参数设置方法［J］.计算机工程，2006，32 （19）：173－175.］