利用多光栅傅里叶频谱的卷积实现数的表达和加密

胡梦莹， 李佳悦， 潘永华

(南京大学 物理学院，江苏 南京210093)

0 引 言

在阿贝成像实验中，通过对物面上光栅进行调制，并研究光栅傅里叶频谱的卷积图像，可以延伸出大量有趣而有应用价值的拓展［1-6］。本实验搭建一个简单的光路系统，如图1 所示。在物面上放上光栅，激光器发出的激光经过透镜组扩束后垂直照在光栅上，首先从两光栅频谱的卷积定理出发，研究了多光栅傅里叶频谱的卷积图像，然后利用这种图像特征，通过对各个光栅与水平方向夹角的调制，赋予其频谱面上各分立谱图像及其特定角度以某种定义，实现了数的表达以及加密的功能，最后探讨了这种全新方案的优越性。

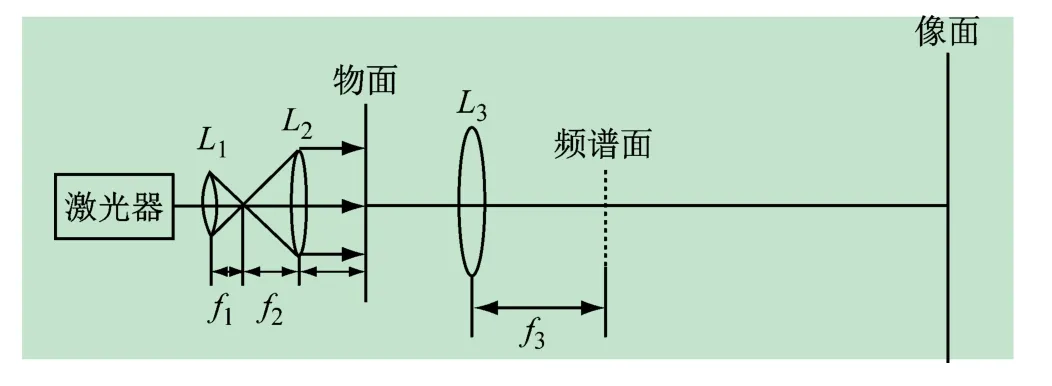
图1 实验的光路系统图

1 多光栅傅里叶频谱的卷积

1.1 阿贝成像原理［7，8］

在相干光照射下，显微镜物镜成像过程可以看作二次衍射过程。第一次衍射发生在物平面到物镜后焦面，通过物的衍射光在物镜后焦面上形成夫琅禾费衍射图;第二次衍射发生在物镜后焦面到像平面，将物镜后焦面上夫琅禾费衍射图上各点发出的球面波在像平面上相干叠加复合为中间像，可以通过目镜观察到。这两个过程本质就是两次傅里叶变换。其物光精确的傅里叶变换关系［9］为:

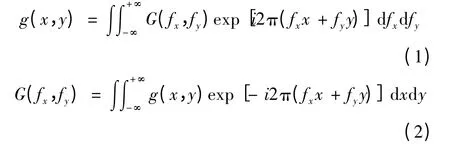
其中:fx，fy是x 和y 方向的空间频率，g(x，y)是物平面的光场复振幅分布;G(fx，fy)是g(x，y)的空间频谱。

1.2 卷积定理［10］

设有两个二维函数g(x，y)和h(x，y)，它们的傅里叶频谱分别为G(fx，fy)和H(fx，fy)，即

其中，F［］表示傅里叶变换。

根据卷积的定义(以* 表示):

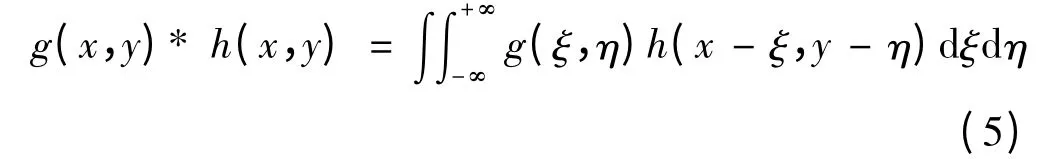
则有

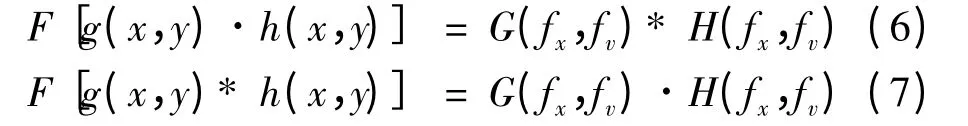
由此可知，若物面上复振幅分布为g(x，y)与h(x，y)之乘积，则由卷积定理可知在频谱面上将观察到的复振幅分布将是他们各自频谱的卷积［11］，同样若在物面上是g(x，y)和h(x，y)的卷积，则在频谱面上观察到的将是他们各自频谱的乘积。

实验中分别将两个具有不同空间频率的一维光栅放入光路中作为物，设g(x，y)为高频300 条/mm 一维光栅，h(x，y)为低频100 条/mm 一维光栅，分别观察其频谱G(fx，fy)、H(fx，fy)，如图2 所示。然后将两光栅重叠在一起作为物，则总的振幅透过率为两光栅各自振幅透过率之乘积g(x，y)·h(x，y)，在频谱面上则可观察到两光栅各自傅里叶频谱的卷积G(fx，fy)*H(fx，fy)，如图3 所示。

图2 两个一维光栅各自的频谱图

图3 两个一维光栅频谱的卷积图像

1.3 卷积定理的推广——多光栅傅里叶频谱的卷积

在物理学中，任何一个符合叠加原理的线性系统都存在卷积［12］。一般来说，卷积是一种通过两个函数f 和g 生成第三个函数的数学算子，表征函数f 与经过翻转和平移的函数g 的重叠部分的面积。如果将参加卷积的一个函数看做区间的指示函数，则卷积还可以看做是“移动平均”的推广。数学上，卷积运算满足交换律和结合律，也即可以实现多个函数的连续卷积运算，所有参与卷积的函数地位相同。

在光学上，为了实现卷积，应用以下傅氏变换公式［13-14］:

式中:A(νX)是a(x)的傅氏变换;F 表示傅氏变换;νX是空间频率。故我们完全可以将1.2 中2 光栅傅里叶频谱的卷积推广到多个光栅［15］。在实验条件足够理想时，4 个光栅、5 个光栅乃至n 个光栅傅里叶频谱的卷积图像都有望实现。

本文通过实验观测到了3 个一维光栅(空间频率分别为300 条/mm、100 条/mm 以及10 条/mm)傅里叶频谱的卷积图像，如图4 所示。

图4 3 个光栅傅里叶频谱的卷积图像

2 利用多光栅傅里叶频谱卷积实现数的表达

2.1 基本思想

空间频率越大的光栅，其衍射分立谱的间距越大。如果在物面上先放置一个空间频率最大的一维光栅G1，再放置一个空间频率第二大的一维光栅G2，此时在频谱面上就可以得到它们各自频谱的卷积图像。保持G1 不动，旋转G2，可以观察到G2 的分立谱绕着G1频谱的每个点转动，即与G1 频谱的夹角发生变化。再加入一个空间频率第三大的一维光栅G3，此时频谱面上即为3 个光栅傅里叶频谱卷积图像。保持G1、G2固定不动，旋转G3，则G3 的分立谱也会绕着G1、G2傅里叶频谱卷积图像的每个频谱点转动。按照同样的方式，保持先加入的光栅固定不动，依次加入并转动空间频率由大到小的一维光栅，便可观察到同样变化规律的现象。

基于上述方式调制光栅，通过定义一种简明的规则，即可实现数的表达。规则如下:将各个光栅的分立谱图像与十进制数的各个数的位权相对应，通过依次调制各一维光栅与水平轴之间的夹角得到特定的频谱分布图，并认为不同夹角表示不同的数值，再将各个数乘以各自的位权后相加，即可得到一个特定的数，从而在多光栅傅里叶频谱卷积图像上实现了数的表达。

2.2 实验实现

首先水平放置空间频率最大的一维光栅G1(300条/mm)，频谱如图5 所示。再水平放置空间频率第二大的一维光栅G2(100 条/mm)，它们频谱的卷积图像如图6 所示，规定该频谱图像表示0 ×10°。

图5 300 条/mm 一维光栅频谱图

图6 0 ×10°的频谱图像

再旋转G2，规定其分立谱与水平轴(即最大空间频率光栅G1 分立谱位置)夹角α 为π/10、2π/10、3π/10、4π/10、5π/10、6π/10、7π/10、8π/10、9π/10 依次表示1 ×10°、2 ×10°、3 ×10°、4 ×10°、5 ×10°、6 ×10°、7 ×10°、8 ×10°、9 ×10°。此时G2 的分立频谱所代表的位权为10°。通过两光栅傅里叶频谱卷积图像，即可表示0 ～9 的所有整数。频谱图像如图7 所示。

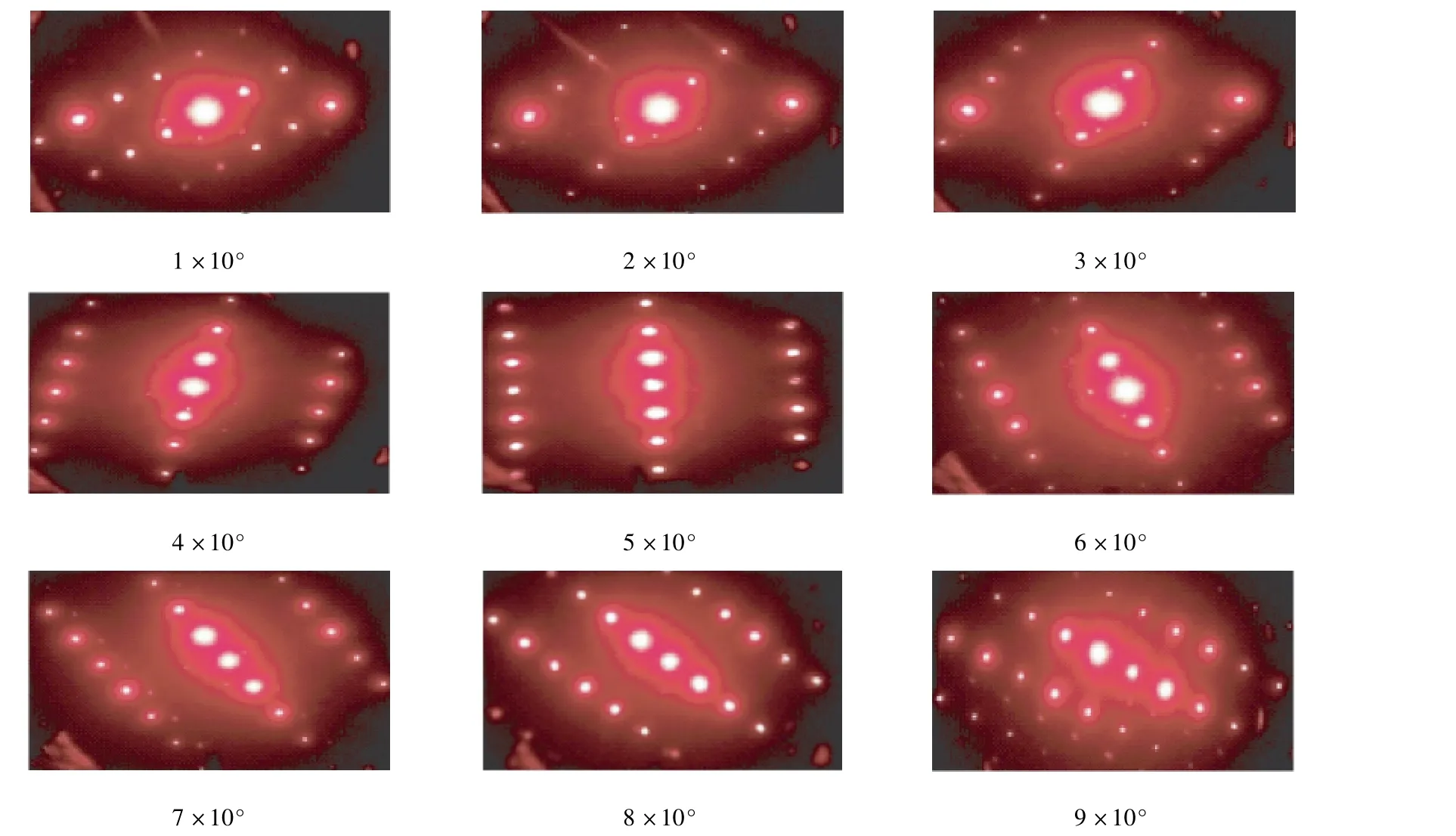
图7 表示0 ～9 的傅里叶频谱卷积图像

利用多光栅傅里叶频谱卷积图像可以实现更高位的数的表达。加上空间频率第三大的一维光栅G3(10条/mm)，在保持G1、G2 固定不动的基础上旋转G3，规定其分立谱与水平轴夹角β 为0、π/10、2π/10、3π/10、4π/10、5π/10、6π/10、7π/10、8π/10、9π/10 依次表示0、1 ×101、2 ×101、3 ×101、4 ×101、5 ×101、6 ×101、7 ×101、8 ×101、9 ×101。此时G3 分立频谱所代表的位权为101，3 个光栅傅里叶频谱卷积图像所表示的数即为β×10/π×101+α×10/π×100。所以，利用三个光栅傅里叶频谱卷积图像，即可表示0 到99 间所有整数。例如，如图8 所示，α =5π/10，β =8π/10，所表示的数即为8 ×101+5 ×100=85;如图9 所示，α =7π/10，β=2π/10，所表示的数即为2 ×101+7 ×100=27;如图10 所示，α=7π/10，β =5π/10，所表示的数即为5 ×101+7 ×100=57。

图8 表示85 的傅里叶频谱卷积图像

图9 表示27 的傅里叶频谱卷积图像

图10 表示57 的傅里叶频谱卷积图像

依照上述规定，依次加入并旋转空间频率由大到小的各个光栅，将每个角度所表示的数乘以各自的位权后相加，即可得到更高位的数。理论上，可利用n 个光栅傅里叶频谱卷积图像来表示0 ～10n－1－1 之间的所有整数，即利用多光栅傅里叶频谱卷积实现了数的表达。

3 利用多光栅傅里叶频谱卷积实现数的加密

在某种规则下，多光栅傅里叶频谱的卷积图像可以表示数。由于这种方式是用图来间接地表示数，并且若不熟悉规则就不可能知道表达的数是什么，所以完全可以将其作为一种数的加密手段，而多光栅傅里叶频谱卷积图像就是藏有密码信息的“加密图”。

3.1 基本思路

加密的关键在于规则的制定与应用。为使得这种基于光栅调制的加密方式具有较强的安全性与灵活性，制定了以下规则:

(1)用各个光栅的分立谱图像与水平轴之间的特定夹角表示特定数值。这种规则使得加密方式灵活多变:例如，加密者可以用夹角为0π/10、1π/10、2π/10、3π/10、4π/10、5π/10、6π/10、7π/10、8π/10、9π/10 的光栅分立谱图像依次表示数0、1、2、3、4、5、6、7、8、9，也可用来表示9、8、7、6、5、4、3、2、1、0，或用来表示0、2、4、6、8、1、3、5、7、9，等等。另外还可以用其他夹角来表示数字:如完全可以用1π/8 来表示1，等等。总之，夹角与数值的对应关系完全由加密者所确定。

(2)将各个光栅的分立谱图像与各密码数的排列位置相对应。在(1)中已明确了各个光栅的分立谱图像与水平轴之间的特定夹角所表示的数，加密者可再制定规则来确定每个光栅的分立谱图像所对应各个数的排列顺序。例如，可令空间频率第二大的一维光栅的分立谱代表密码的第一个数，空间频率第三大的一维光栅的分立谱代表密码的第二个数……，以此类推，空间频率最小的光栅分立谱代表密码的最后一个数。加密者便可通过第2 节中方式依次调制光栅，使得到的多光栅傅里叶频谱卷积图像即为某个特定密码的“加密图”。同样，确定数的排列顺序的规则也是灵活多变的:完全可以用空间频率第二大到最小的光栅的分立谱倒序表示密码，这样同一幅图所存储的密码的顺序相反。如果再采用另外的规则来确定各密码数的排列顺序，则同一幅图所存储的密码又会改变。由于规则的制定方式由加密者确定，这大大增加了解密难度。

(3)若密码数较多，还可用多幅多光栅傅里叶频谱卷积图像实现加密。由于每幅卷积图像所能存储的数字信息量是有限的，可以让每幅图存储密码的某一部分，而完整的密码内容就是每幅图像存有密码的某种组合。加密者可自行规定每幅图存储的是密码的哪一部分，这个不确定因素使得加密程度进一步加深，解密难度也进一步加大。

3.2 实验实现

(1)利用一幅3 个光栅傅里叶频谱的卷积图像实现对2 位密码的加密

加密者采用如下规则:夹角为0π/10、1π/10、2π/10、3π/10、4π/10、5π/10、6π/10、7π/10、8π/10、9π/10的光栅分立谱图像依次表示数0、1、2、3、4、5、6、7、8、9，并规定空间频率第二大的一维光栅的分立谱表示密码的第一个数，空间频率第三大的一维光栅的分立谱表示密码的第二个数。则若要对密码75 实现加密，可用第2 节中的方式依次调制光栅G1、G2、G3，使得α =7π/10，β=5π/10，如图11 所示，该3 光栅傅里叶频谱卷积图像即为存有密码75 的“加密图”。

图11 存有密码75 的“加密图”

由于规则为加密者灵活制定，所以如果加密者变换加密规则，那么图11 解密后将是另外一个密码。例如，加密者用夹角为0π/10、1π/10、2π/10、3π/10、4π/10、5π/10、6π/10、7π/10、8π/10、9π/10 的光栅分立谱图像依次表示数9、8、7、6、5、4、3、2、1、0，则图11就变为存有密码24 的“加密图”;或者加密者若不改变上段中各夹角的光栅分立谱图像所表示的数，而是改变各个光栅的分立谱图像与各密码数的排列位置的对应关系，如用空间频率第二大的一维光栅的分立谱表示密码的第二个数，空间频率第三大的一维光栅的分立谱表示密码的第一个数，则图11 就成为存有密码57的“加密图”。所以，一幅多光栅傅里叶频谱卷积图像可实现对不同密码的加密。同样，同个密码也可以用不同的多光栅傅里叶频谱卷积图像实现加密。由于真正存储的密码取决于加密者制定的规则，而这规则千变万化，故成功解密的难度非常大，密码的安全性很高。

(2)对多位密码进行加密。若加密者要对多位密码进行加密，可利用多幅多光栅傅里叶频谱卷积图像。

例如，加密者要对6 位密码进行加密，可利用3 幅3 个光栅傅里叶频谱卷积图像，每幅图存有其中2 位密码。如果对于每个2 位密码加密方式都采用如同2.2 节中密码75 的“加密图”的加密规则，并令从左往右排列的3 幅图分别存有6 位密码的第一第二位、第三第四位和第五第六位，则若要对密码725855 实现加密，可用第2 节中方式依次调制光栅，得到3 幅3 光栅傅里叶频谱卷积图像并依次排列，如图12 所示，这3幅从左往右排列的三光栅傅里叶频谱卷积图像即为密码725855 的“加密图”。

图12 存有密码725855 的“加密图”

事实上，加密者还可以规定从左往右排列的3 幅图分别存有密码的第一第六位、第二第五位、以及第三第四位，则图12 实现了密码755582 的加密。或改变读图顺序，令从右往左排列的三幅图分别存有密码的第一第二位、第三第四位和第五第六位，则图12 又成为密码555872 的“加密图”。仅仅是改变每幅图所存有的密码的排位或读图的顺序，3 幅3 个光栅傅里叶频谱卷积图像就可实现多个不同的六位密码的加密，若再改变每一幅图的加密规则，则利用这3 幅3 个光栅傅里叶卷积图像可实现非常多种不同的六位密码的加密。同时，同一个密码还可以用不同的多幅多光栅傅里叶频谱卷积图像实现加密。所以，利用多幅多光栅傅里叶频谱的卷积图像实现加密的安全性比利用一幅要高得多，破解密码难度极大。

3.3 用此种方式实现加密功能的优越性

本实验利用多光栅傅里叶频谱卷积图像实现加密，其优越性体现在以下几点:

(1)通过各光栅频谱图与水平方向夹角来存储数字，在实验上易于实现，且现象清楚明显，既易于调制，也易于读取。

(2)基于此种光栅调制方式，可定义各种规则进行加密。规则的任意性、复杂性和可灵活变换性，大大地增强了加密强度，也大大提高了密码信息存储的安全性。加密者可任意改变规则，只有在特定时间知道该时间段特定规则的人，才可以成功解密。

4 结 语

本文从卷积定理的推广，在实验上研究并验证了多光栅傅里叶频谱的卷积图像。利用多光栅傅里叶频谱的卷积图像的特性，通过依次调制物面上各个光栅与水平方向的角度，并赋予其频谱面上各光栅分立谱图像以及分立谱图像的特定角度以某种定义，创造出了一种全新的多位数的表达方式。同时还提出，利用这种调制方式，加上灵活多变的定义规则，可以实现数字密码的加密，而该种加密方式安全可靠，其优越性是显而易见的。

［1］ 余 欣，潘永华. 光的三进制逻辑运算与光学加密［J］. 物理实验，2008，28(3):1-8.

［2］ 王汉琛，刘 璟，潘永华，周 进.运用阿贝成像原理进行平面密铺结构的频谱分析［J］.2011，31(10):5-10.

［3］ 李芳菊，董康军.利用阿贝成像原理制作低频全息光栅［J］.物理实验，2008，28(5):1-3.

［4］ 冯少彤.互补分形图像的光学傅里叶变换［J］. 激光杂志，2003，24(1):27-28.

［5］ 王 翚，刘香茹，石发旺. 利用阿贝成像原理制作全息光栅的理论分析［J］.河南科技大学学报(自然科学版)，2006(2):1-3.

［6］ 袁 霞，王晶晶，金华阳. 阿贝成像原理和空间滤波实验的改进［J］.物理实验，2010，30(3):1-3.

［7］ 高文琦等. 光学(第三版)［M］. 南京:南京大学出版社，2013:250-251.

［8］ 赵凯华，钟锡华.光学(下册)［M］.北京:北京大学出版社，1984:75-77.

［9］ 梁昆淼，刘 法，缪国庆.数学物理方法［M］.3 版.北京:高等教育出版社，1998:102.

［10］ 苏为宁，王思慧，高文莉，等编. 大学物理实验(理科)第二册［M］.南京:南京大学出版社，2014:130.

［11］ 潘元胜，冯璧华，于 瑶.大学物理实验(第二册)［M］.南京:南京大学出版社，1998:102.

［12］ 毛惠良，多重卷积公式及其应用［J］. 工科数学，1995，11(3):173-176.

［13］ Jack. D. Gaskill. Linear systems，Fourier transforms，and optics［M］. Arizona:John Wiley ＆ Sons，Inc，1978，160-201.

［14］ 冯光彤，金国钧，章程军，等. 光学分形图像的产生［J］. 中国激光，1997，24(8):2.

［15］ 高 峰.傅里叶变换透镜参数的研究［J］. 实验室研究与探索，1997(6):59-60.