代理计算签名及其在RFID认证中的应用

高员，李琳，肖静，赵成志

（工业和信息化部电子第五研究所，广东 广州 510610）

代理计算签名及其在RFID认证中的应用

高员，李琳，肖静，赵成志

（工业和信息化部电子第五研究所，广东 广州 510610）

射频识别 （RFID）是物联网中实现物品标识的一项关键技术，但RFID标签的计算能力十分有限，导致传统的公钥密码技术很难有效地应用到RFID认证技术中，限制了RFID的应用范围和提供服务的形式。针对读卡器和标签计算资源不对称的特点，提出一种新的签名算法——代理计算签名，将传统的签名技术中耗能的复杂运算交给读卡器 （验证方）来完成，从而实现标签对消息的签名，并仍能保持签名的安全性，解决了RFID标签很难计算数字签名的困难问题。结合Rabin型数字签名和加密算法，进一步地给出了基于代理计算签名的RFID认证方案，实现了标签与读卡器间的双向认证，大大地降低了标签的实现成本。

射频识别；代理计算；签名；认证

0 引言

射频识别技术 （RFID）是物联网[1]中实现物品标识的一项关键技术[2]，由标签、阅读器和天线3个部分组成[3-4]。它利用射频信号通过空间耦合 （交换磁场或电磁场）来实现无接触信息传递，并通过所传递的信息达到识别的目的。射频识别技术已被广泛地应用于工业自动化、商业自动化、交通运输控制管理、军事、商品防伪、监视、定位和工业等众多领域。

由于RFID系统的标签资源有限、标签信息易被非授权访问，解决RFID中标签与读卡器之间的相互认证和信息保密就成为扩展RFID应用的关键问题。

本文针对读卡器和标签计算资源不对称的特点，提出一种代理计算签名算法，将传统的签名计算中耗能的复杂运算交给读卡器 （验证方）来完成，从而实现标签对消息的签名，并仍能保持签名的安全性。结合Rabin数字签名和加密算法[5]，本文进一步地给出基于代理计算签名的RFID认证方案，实现了标签与读卡器之间的双向认证，解决了RFID标签资源有限的问题。

1 代理计算签名算法

本文提出的代理计算签名算法是基于椭圆曲线签名算法ECDSA[6-8]设计的。

1.1 代理计算签名算法设计

1.1.1 密钥生成

用户A具有域参数组D=（q，FR，a，b，G，n，h），对消息m进行签名。A在区间 [1，n-1]内选择随机整数 （x，t），计算Q=xG=（x1，y1），T=t-1G=（x2，y2）； （Q，T）为公钥， （x，t）为私钥，其中：x为签名私钥，t为掩蔽私钥。

1.1.2 代理计算签名

a）签名者A选取秘密随机数k，1≤k≤n-1，计算u=kt mod n，发送u给签名验证者B。

b）B计算uT=（x3，y3），将x3转换为整数，计算r=x3mod n。若r=0，则返回步骤a），A重新选择随机数k；否则B将r发送给A。

c）A以k作为会话密钥，计算s=k-1（H（m）+rx）mod n。若s=0，则返回步骤a），A重新选择随机数k；否则 （s，r）即为用户A对消息m的签名。

1.1.3 验证签名

为验证用户A对消息m的签名 （s，r），用户B需获得A的公钥 （Q，T）和域参数组D=（q，FR，a，b，G，n，h），并对D和 （Q，T）的有效性进行确认，然后用户B进行如下操作：

a）计算w=s-1mod n。

b）计算u1=H （m）w mod n，u2=rw mod n。

c）计算X=u1G+u2Q。

d）若X=0，则为非法签名；否则将X的横坐标转换为整数x1，并计算v=x1 mod n。

e）若v=r，则接受签名。

1.2 代理计算签名算法分析

1.2.1 签名的正确性分析

若签名 （s，r）确实是消息m的合法签名，则s=k-1（H（m）+rx）mod n，重新整理得：

k=s-1（H （m）+rx）=s-1H （m）+s-1rx=w H（m）+ wrx=u1+u2xmod n

于是X=u1G+u2Q=（u1+u2x）G=kG，uT=ktT= ktt-1G=kG，因此v=r为所需。

1.2.2 签名的安全性分析

本文提出的代理计算签名主要用于解决诚实的验证者对签名者真实性的验证问题，因此，代理计算签名的安全性问题主要考虑签名的不可伪造性问题。以下我们基于ECDSA签名给出两个定理，以说明代理计算签名的安全性。

a）定理1：如果ECDSA签名是安全的，则基于ECDSA的代理计算签名也是安全的。

证明：如果ECDSA签名是安全的，则表明ECDSA签名是不可伪造的。即给定消息m，不具有私钥x的人无法产生m的正确ECDSA签名，或找到两个不同的消息使其具有相同的签名在计算上不可行。在本文的代理计算签名中，s的计算是由签名者本人完成的，r的运算通过了验证者的代理计算。由于r是可以公开的，因此，对于定理1只需证明，攻击者由计算r的两个参数u=kt mod n和T计算出k在计算上是不可行的。

由T计算t需要解决ECDLP问题，并需要进行求逆运算，而在mod n运算下任选k′都存在t′，使得k′t′≡kt mod n，因此，攻击者只能通过验证所选t′是否满足T=t′-1G来判断所选取t′的正确性。但是，如果攻击者能够在多项式时间内判断出正确的t，则破解了ECDLP问题。因此，这是不可行的，也即在多项式时间内由代理计算中的两个参数计算出签名所使用的正确的k是不可行的。所以结论成立。

b）定理2：如果ECDSA签名是安全的，则在相同的掩蔽私钥t下，即使攻击者获得多个代理计算请求参数u1=k1t mod n，u2=k2t mod n，…，uh=kht mod n和T，h是产生代理计算签名的次数，所产生的所有代理计算签名也都是安全的。

证明：同定理1的证明思路，这时只需证明，攻击者由获得的多个代理计算请求参数u1=k1t mod n，u2=k2t mod n，…，uh=kht mod n和T计算出k在计算上是不可行的。在mod n运算下任选t′都存在一组对应的随机数k1′，k2′，…，kh′，使得k1′t′，k2′t′，…，kh′t′等于k1t，k2t，…，kht，这只需令ki′=kitt′-1，i=1，2，…，h。因此，攻击者只能通过验证所选t′是否满足T=t′-1G来判断所选取t′的正确性。但是，如果攻击者能够在多项式时间内判断出正确的t，则破解了ECDLP问题。因此，这是不可行的，也即在多项式时间内由代理计算中获得的多个参数计算出签名所使用的正确的会话密钥k1，k2，…，kh是不可行的。所以结论成立。

2 基于代理计算签名的RFID认证方案

基于上一章节的代理计算签名算法，结合Rabin公钥体制，本章设计将标签中的复杂运算交给读卡器来完成的RFID认证方案。

RFID系统采用基于证书的方式来管理密钥，可信第三方 （CA）基于Rabin型数字签名来管理证书，其私钥是 （p，q），公钥是nCA=pq。

读卡器采用Rabin公钥加密体制[5]，CA为读卡器颁发的签名证书标记为Certr，私钥是 （e，d），公钥是nr=ed。

标签采用代理计算签名体制，CA为标签颁发的签名证书标记为Certt，私钥是 （x，t），公钥是（Q=xG，T=t-1G），椭圆曲线域参数D=（q，FR，a，b，G，n，h）。

2.1 RFID双向认证方案设计

2.1.1 初始化

系统为每一个标签和读卡器分配一个惟一的标识码，分别用UIDt和UIDr表示；选择hash链作为随机数产生器PRNG（） （即每次选取的随机数都是对上次通信所选随机数hash值的计算），一个对称加密算法 E，hash函数H（）。 将 [nCA， nr，UIDr，H（）]存入到标签的存储器中，将 [nCA，Q，T，UIDt，H（）]存入到读卡器中。

2.1.2 标签与读卡器的双向认证过程

RFID标签与读卡器相互认证过程如图1所示。

图1 RFID标签与读卡器相互认证过程示意图

a）读卡器选取随机数z，向标签发起认证请求，将 （Query，Certr，z）发送给标签。

b）标签用CA的公钥nCA对该证书加以验证，若成立，则说明该读卡器是经过可信第三方认证的授权读卡器。标签选取随机数f作为后续通信的会话密钥 （对称密钥），利用公钥nr对f进行Rabin型公钥加密，即计算a=f（f+z）mod nr，其中z是对f进行Rabin型公钥加密时选取的随机数。标签选取秘密随机数k，1≤k≤n-1，计算u=kt mod n，将 （a，b）=Ef（u，Certt）发送给读卡器。

c）读卡器收到 （a，b）后，首先，用私钥（e，d）解密a得出f，并检验随机数z的正确性；然后，用f解密b得到 （u，Certt），验证证书Certt后，计算uT=（x3，y3），将x3转换为整数，计算r= x3mod n。若r=0，则返回a），标签重新选择随机数k；否则，读卡器将f的hash值H（f）、Ef（r||H（r）） （其中H（r）是为了保护消息完整性）发送给标签。

e）标签收到H（f）′后，验证H（f）′=H（f）是否成立。若不成立，则终止通信；否则，完成标签对读卡器的认证。标签对E f（r||H（r））解密后得到r，计算s=k-1（H（f）+rx）mod n， （s，r）即为标签对会话密钥f的签名，将 （s，r）发送给读卡器。

f）读卡器收到 （s，r）后，验证签名 （s，r）是否有效，若有效，完成读卡器对标签的认证；否则，终止通信并审计。

2.2 RFID双向认证方案分析

2.2.1 安全性分析

本文提出的RFID认证方案，不仅能够实现信息的保密功能及标签与读卡器之间身份的相互认证，还能够满足抵抗信息泄露、窃听、重放攻击、流量分析攻击和前向攻击等安全要求。本节中我们将对RFID认证协议所能抵抗的各类攻击进行分析：

a）防止非法读取

因为标签和读卡器都需先进行身份认证，才能相互交换数据，因此，可以有效地防止非法读取。

b）防止窃听

由于读卡器和标签之间的通信信道是不安全的信道，所以非法用户可以访问该信道。在方案第1步中，读卡器发送的Certr是经过CA签名的公钥证书，在第2步中读卡器需对随机数z的正确性进行验证。因此，第1步中发送的消息 （Query，Certr，z）都是可以对外开放的，在后续通信中，标签与读卡器间通信时发送的是hash值和加密的信息，非法用户不能窃听到数据内容。

c）前向安全性

如果一个非法用户可以破坏一个标签，拥有它现在保存的全部数据，那么它就可以追踪该标签以前的会话，这就是前向攻击。在本章的方案中，由于随机数使用的是hash链，所以标签每次选取的随机数f和k都与上次不同，即使攻击者截取了某次标签的输出，也不能根据此值推算出标签以前的输出，因此，可以有效地防止前向攻击。

e）防止重放攻击

攻击者事先记录标签发出的信息，当读卡器与标签再次通信时，攻击者通过记录下的标签信息来伪装成合法标签与读卡器进行通信。但是，由于标签中的随机数构建了一个hash链，保证了每次通信时使用的随机数是不同的，因此，攻击者记录的信息不会被再次利用。读卡器可以使用随机数z来判断收到的消息a是否被重放。

f）防止位置追踪

由于在当前的协议中，标签在每次通信中输出的信息都是不固定的，并且hash函数的输出也是不可预知的，因此，攻击者无法根据固定的输出来对标签的位置进行跟踪。

2.2.2 性能分析

RFID安全认证协议不仅要解决安全性方面的问题，由于RFID标签的有限存储容量和计算能力，认证协议也必须在计算时间和存储容量方面进行考虑，尽量使标签的计算量不要过大，存储数据尽量地少，这样才能最大程度地降低标签的成本，从而降低整个RFID系统的成本。下面我们通过统计标签在整个认证过程中所需的计算量来对协议进行评估。表1即为整个认证过程中标签涉及到的计算。

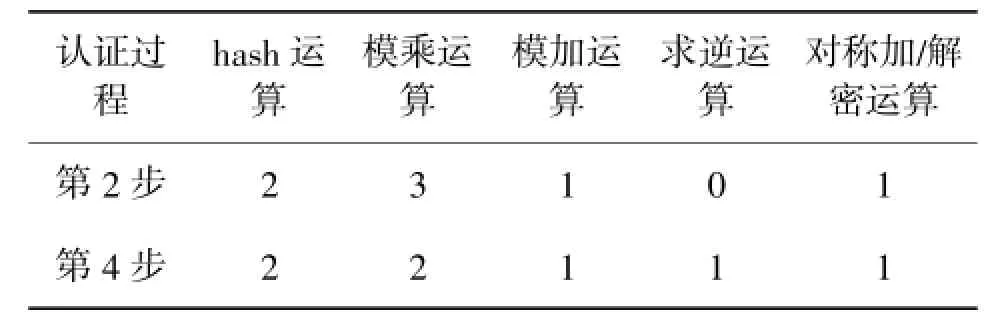
表1 标签在基于公钥的RFID认证方案中的计算量

在验证读卡器的公钥证书和建立会话密钥的过程中，标签需要进行一次模nCA上的平方运算、一次hash运算和模nr上的一次加法、一次乘法运算。

在整个代理计算签名技术实现的过程中，标签需要进行3次hash运算、1次对称加密运算、1次对称解密运算和模n上的1次求逆运算，以及3次乘法运算、1次加法运算。

3 结束语

本文提出了一种代理计算签名技术，并将其应用到RFID认证当中，实现了读卡器和标签的、基于公钥技术的双向认证。该技术解决了读卡器不能进行复杂耗能运算的困难问题，使得RFID系统的标签管理更加方便、灵活。在本文给出的RFID认证方案中，标签所需要的运算量非常小，既保障了系统实现的灵活性和可扩展性，又极大地降低了标签的实现成本。如何设计更为安全、高效的代理计算签名，以及如何实现对RSA类签名的代理计算都是值得进一步研究的问题。

[1]AKYILDIZ I F，SU W，SANKARASUBRAMANIAM Y，et al.Wireless sensor networks：a survey[J].Computer Networks，2002，38：393-422.

[2]陈积明，林瑞仲，孙优贤.无线传感器网络的信息处理研究 [J].仪器仪表学报，2006，27（9）：1107-1111.

[3]游战清，李苏剑.无线射频识别技术 （RFID）理论与应用 [M].北京：电子工业出版社，2004.

[4]周晓光，王晓华，王伟.射频识别 （RFID）系统设计、仿真与应用 [M].北京：人民邮电出版社，2008.

[5]HANKERSON D，MENEZES A，VANSTONE S.椭圆曲线密码学导论 [M].张焕国，译.北京：电子工业出版社，2005：22-66.

[6]MILLER.V.Use of elliptic curves in cryptography[C]// Advances in Cryptology-Proceedings of CRYPTO’ 85. 1986：417-426.

[7]KOBLITZN.Elliptic curve cryptosystems[J].Math.Comp.，1987，48（5）：203-209.

[8]RABIN M O.Digitalized signatures and public-key functions as intractable as factorization[R].MIT/LCS/TR-212，MIT Laboratory for Computer Science，1979.

Com puting-Comm ission Signature and its App lication in RFID Authentication

GAO Yuan，LILin，XIAO Jing，ZHAO Cheng-zhi
（CEPREI，Guangzhou 510610，China）

RFID is one of the key technologies for items identification in Internet of things，while the limited computing ability of RFID tagsmake it difficult to apply traditional public key cryptography to RFID authentication efficiently， which greatly limits the scope of RFID applications and the forms of providing services.A new signature algorithm called computingcomm ission signature algorithm is p resented aim at the character that the computing resources of readers and RFID tags are asymmetric.In our signature algorithm， we leaved the complex energy-consuming computation in traditional signature algorithm to the verifier（readers）so that the signature can be generated on tags and the security of the signature is still satisfied.Our signature algorithm solved the difficult problem of computing digital signature in RFID tags. Combining with Rabin-type signature and encryption algorithm，a RFID authentication schem e based on computing-comm ission signature is further proposed，which achieved mutual authentication between readers and tags.It greatly reduced the implementation cost of tags.

Radio Frequency Identification（RFID）；computing-commission；signature；Authentication

TP 309

：A

：1672-5468（2015）01-0024-06

10.3969/j.issn.1672-5468.2015.01.006

2014-08-27

2014-12-30

高员 （1986-），女，河北衡水人，工业和信息化部电子第五研究所软件质量工程研究中心助理工程师，硕士，主要从事信息安全等级保护测评、公钥密码学与信息安全等研究工作。