对一道物理竞赛题的两种互异解答的探讨
郑 金
(凌源市职教中心 辽宁 朝阳 122500)
对一道物理竞赛题的两种互异解答的探讨
郑 金
(凌源市职教中心辽宁 朝阳122500)
摘 要:针对一道竞赛题的两种不同的解答得出两个相反的结果,通过深入辨析原因,多角度探究了恒速参考系中做往复运动物体的机械能守恒的条件以及弹簧的弹性势能与系统的弹性势能的异同.
关键词:竞赛题参考系机械能守恒
对于第26届全国中学生物理竞赛复赛第三题第1小题,原参考答案虽然正确,但只有定性分析,没有进行定量解答;此外,在一些文献所给出的答案中,既有正确的,也有错误的,下面对两种结果不同的解法进行探讨.
【题目】一质量为m的小球与一劲度系数为κ的弹簧相连组成一体系,置于光滑水平桌面上,弹簧的另一端与固定墙面相连,小球做一维自由振动.试问:在一沿此弹簧长度方向以速度u做匀速运动的参考系里观察,此体系的机械能是否守恒,并说明理由.
参考答案:否.原因是墙壁对于该体系而言是外界,墙壁对弹簧有作用力,在运动参考系里此力的作用点有位移,所以对体系做功,从而改变这一体系的机械能.
从该答案来看,原题是一道比较简单的竞赛题.下面展示两种难度较大的定量解法,并指出其中的不足之处.
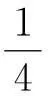
设弹簧位于墙壁的右侧,参考系向右运动,弹簧的形变量为
Δx=Δxmcosωt
则墙壁对弹簧的弹力为
F=κ·Δx=κ·Δxmcosωt
在运动参考系中,弹簧与墙壁的接触点向左运动,位移为x=-ut,则墙壁对弹簧所做的功为
W=Fx=-Fmutcosωt=-f(t)t
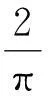
所以墙壁的弹力所做的功为
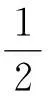
这恰好等于墙壁弹力对弹簧所做的功.
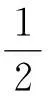
求墙壁弹力所做的功还有一种方法.
设弹簧的伸长量为Δx,在从原长状态到最大伸长量的过程中,墙壁对弹簧的弹力为
F=-κΔx=-κΔxmsinωt
弹簧与墙壁接触点的位移为x=-ut,是关于时间的一次函数,因此墙壁弹力所做的功为
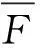
这表明,在恒速参考系中,墙壁弹力对弹簧所做的功与小球的质量、速度以及参考系的速度有关.也可说成是墙壁对小球间接做功,称为“借物传功”.
解法2:如图1所示,水平弹簧振子在平衡位置O(设为地面坐标系原点)两侧做简谐运动,小车以速度u向右运动,以小车为参考系,即坐标原点O′在小车中心,刚开始时O′与O重合,且坐标轴x′随小车一起向右运动,则墙壁对弹簧的作用点以速度u向左运动,发生位移,因此墙壁对弹簧的作用力是做功的.
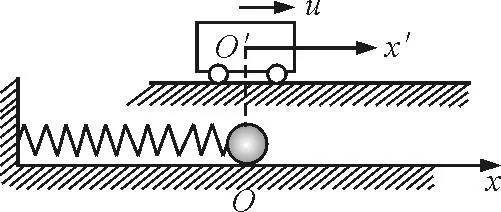
图1
开始相对运动后,当t=0时,将小球向右拉至最大位移即振幅A并放手,使之做简谐运动,在小车参考系上观察(即以小车参考系为静止参考系),地面参考系及小球都以速度u相对于小车沿x轴负方向匀速运动,同时小球还有相对于地面的速度v.
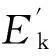
x′=x-ut=Acosωt-ut
v′=-ωAsinωt-u
a′=-ω2Acosωt=a
f=ma′=-mω2Acosωt=-κx
小球的动能为
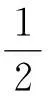
由于弹簧的弹性势能与弹簧的形变量有关,考虑到弹力做正功时弹性势能减少,则弹性势能可用微分来表示为
κxdx-κuAdtcosωt=
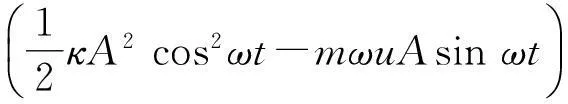
由于当t=0时
则积分常数C=0,因此在时刻t弹簧的弹性势能为
则系统的机械能为
由于这是一个恒定值,所以,在小车参考系上观察时,弹簧振子体系的机械能仍然守恒.
探讨:在上述两种解法中,出现两个不同的结果,那么其中必有一种解法是错误的.
或者说,由于在运动参考系中,弹簧对小球的弹力不是保守力,所以小球对弹簧所做的功不是二体系统的弹性势能.再者,弹簧的弹性势能只与自身的形变量有关,不应随参考系而变化,即为
由伽利略变换及不变性可知
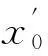
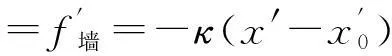
墙壁和小球对弹簧的弹力所做的总功为
即弹性势能的增量为
所以弹簧的弹性势能为
这表明,弹簧所受的一对弹力在恒速参考系中是保守力,做功的多少与路径无关,只与弹簧两端点的位置有关.
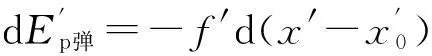
且有等式
这表明,由弹簧、小球和墙壁所组成系统的弹性势能等于弹簧的弹性势能与弹簧对墙壁所做的功之和.所谓系统的弹性势能,是指除动能之外的机械能总和.
当弹簧处于拉伸状态时,受到墙壁的作用力方向向左,而弹簧的固定端点在匀速运动的参考系中运动方向向左,因此做正功,由于相对于地面的速度大小为v=ωAsinωt,利用“借物传功”的结论可知墙壁作用力对小球间接做的功为
W=muv=muωAsinωt
也可视为墙壁对弹簧所做的功,那么弹簧弹力对墙壁所做的功为
W′=-muωAsinωt
由于墙壁的动能保持不变,所以由弹簧、小球和墙壁组成系统的机械能始终守恒.
原题中的由弹簧和小球组成系统的机械能应为
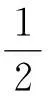
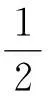
由于在式中含有速度v不是常数,因此在运动参考系中由弹簧和小球组成系统的机械能不守恒.
一般来说,机械能守恒是指整个过程中的各个时刻对应的机械能总量始终保持不变,如果将某一过程中只有两个时刻对应的机械能总量相等也称为机械能守恒,那么该题还有其他解法,现探讨如下.
从解法2的推导过程可知,当u=0时
当u≠0时,只有当ωt=nπ(n为自然数)时,才有
ωt=nπ
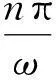
小球的动能为
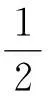
所以系统的机械能总量为
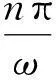
或由此可知,当n=1时
收稿日期:(2015-02-25)
——兼谈参考系与坐标系的关联关系

