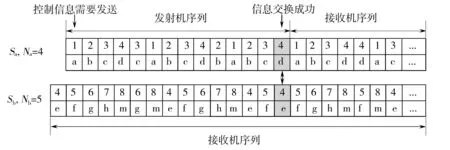
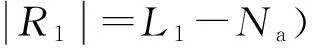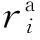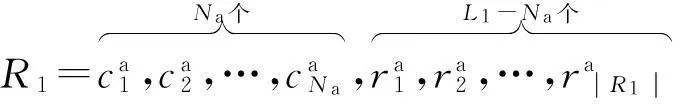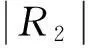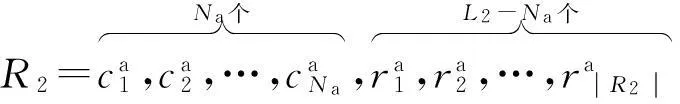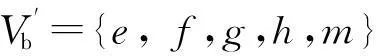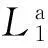基于认知网络不对称模型的交会跳频算法

Foundation items: Supported by the National Natural Science Foundation of China(61072069) and the National Science and Technology Major Project of Ministry of Science and Technology of China(2012ZX03003012)

基于认知网络不对称模型的交会跳频算法*

钟鸣张海林马蓓兰冰

(西安电子科技大学 通信工程学院， 陕西 西安 710071)

摘要：基于认知网络的不对称模型提出了一种新的交会跳频算法(AMCH).该算法根据每个次要用户感知到的可用信道集，在两个不相交的素数集中选择发射机和接收机的跳频序列长度并分别构建跳频序列.在不需要其他辅助信息(如全网同步信息、信道标号信息)的情况下,通信范围内的任意两个次要用户通过跳频于短时间内就能交会在它们的共同信道上并建立通信链路.与现有算法相比,AMCH算法减小了跳频序列冗余,提高了交会效率.仿真结果表明,AMCH算法的交会时间上限最小,交会性能优于现有算法.

关键词：认知无线电；认知无线网络；不对称模型；跳频算法；交会

收稿日期：2014-12-15

基金项目：* 国家自然科学基金资助项目(61072069);国家科技重大专项(2012ZX03003012);西安电子科技大学中央高校基本科研业务费专项资金资助项目(72136037)

作者简介：钟鸣(1981-),男,博士生,主要从事认知无线网络研究.E-mail: ringbel2458_cn@sina.com

文章编号：1000-565X(2015)05-0035-05

中图分类号：TP393

doi:10.3969/j.issn.1000-565X.2015.05.006

收稿日期：2014-12-08

随着无线通信技术的迅速发展,近年来搭载着新兴应用的通信设备大量涌现,迅速地挤占可自由使用的非授权频段;一些利用率较低的授权频段却由于频谱规划准则无法提供给这些通信设备使用[1].为提高频谱资源的使用效率,使更多的无线设备共享授权频段,Mitola等[2]提出了认知无线电.通过认知无线电技术,非授权用户利用频谱空洞动态地接入授权频段进行通信,组成认知网络[3-4].在认知网络中非授权用户被称为次要用户(SU),授权用户被称为主要用户(PU).为了不干扰主要用户的通信,次要用户周期性地感知所有授权频段.若发现某个授权频段没有主要用户,则将其视为可用信道;若发现该授权频段被主要用户占用,则将其视为非可用信道并终止通信.认知网络是特殊的多信道网络,网络中的次要用户随着主要用户随机占用活动动态地调整可用信道集,因此无法使用固定的公共控制信道交换控制信息.这种情况下交会成为代替公共控制信道的最好方法[5].

交会是两个或多个次要用户汇聚在相同信道上的过程.实现交会的方法可分为两类,一类是分簇算法[6-7],另一类是跳频算法[8-12].分簇算法在局部区域内实现了次要用户的交会,但簇群有鲁棒性差的缺陷,任意一个主要用户的随机占用活动都可能使其分解,这将极大地增加协议开销并使通信质量急剧恶化.跳频算法实现了次要用户在时间及频段上的分布式交会,既克服了固定信道交会引起的“单点错误”[13-14],又避免了分簇算法的缺陷.

不对称模型广泛应用于广播、路由以及“蓝牙”传输等方面.基于不对称模型的交会跳频算法需要分别为发送信息的次要用户和接收信息的次要用户分配不同的跳频序列.当需要建立通信链路时,次要用户使用发射机序列跳频,其他次要用户使用接收机序列跳频;当控制信息交换成功后,次要用户将恢复接收机序列跳频.随着对交会问题的深入研究,学者们陆续提出了一些基于不对称模型的交会跳频算法.文献[10]提出的ACH算法利用Quorum系统矩阵为发射机和接收机分别设计跳频序列.Quorum系统具有旋转闭包性,发射机和接收机即使在异步跳频条件下也能交会,但ACH算法生成的跳频序列由所有授权信道组成,当次要用户的可用信道较少时,其交会效率较低.文献[11]提出的ARCH算法利用时钟理论设计跳频序列.其发射机序列是逆时针序列,而接收机序列是顺时针序列.ARCH算法能够保证发射机序列与接收机序列在有限的时间内交会,但认知网络中授权信道数必须是偶数.文献[12]提出的SRB算法中,接收机停留在固定信道上等待发射机交会,当主要用户占用信道时接收机将被迫改变停留信道,故交会受到主要用户随机占用活动的驱使,主要用户越活跃,次要用户的交会时间越短.SRB算法适用于发射机与接收机距离较近,且具有相似网络环境的场景,一旦接收机和发射机的网络环境差异较大且主要用户不活跃时,其交会时间将大大增加.上述算法均假设次要用户的认知设备具有相同的认知能力,故对于异构认知网络(不同类型的次要用户对信道感知范围及对信道标号可能不同),有些算法如文献[11]中算法并不适用.

在兼容异构认知网络的前提下,文中以最短的交会时间(TTR)为目标,提出了基于不对称模型的交会跳频算法(AMCH),以最大程度地利用可用信道集设计跳频序列,提高交会效率,减少交会时间.

1认知网络与时隙通信系统

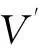
SU在时隙通信系统上跳频.时隙通信系统中的时间被划分为等长的时隙,每个时隙为一个最小的跳频单位.SUa与SUb开始跳频的时隙差为任意数.文献[15]提出了一种时隙差为小数的异步跳频方案,为简单起见,文中假设时隙差为整数k.

2AMCH算法

2.1算法的基本思想

当跳频步长与序列长度互素时,两个信道标号连续的跳频序列能够交会[8-9].当跳频步长与序列长度为不同素数时,不但信道标号连续的跳频序列能够交会并且任意排列的跳频序列也能够交会.为证明以上论述,文中将属于不同跳频序列的信道处于相同时隙的关系称为对应,用%代表取模运算,在此基础上提出了定理1.

定理1周期序列X1由X=c1,c2,…,cx循环相连组成(x为序列X的长度),周期序列Y1由Y=c1,c2,…,cy循环相连组成(y为序列Y的长度).如果x与y为不同素数,则在有限周期内∀ci∈X将对应Y内所有元素.

证明假设在X1的任意一个循环周期内,ci对应cj(cj∈Y),那么在其后的第l1和l2(l1

由定理1可知,只要X和Y的序列长度为不同素数并且存在共同信道,那么任意两个跳频序列就能交会.

2.2算法描述

AMCH算法为SU分配两种跳频序列,当没有信息需要发送时,SU按照接收机序列进行周期跳频;当有信息需要发送时,SU按照发射机序列进行周期跳频.令P={2,3,5,7,11,13,…,p}(p≥N)为按顺序排列的有限素数集,任意SUa的发射机序列和接收机序列生成算法的步骤如下:

(1)将P按元素排列的奇偶位置划分为两个新的素数集P1与P2,P1={2,5,11,…,p1},P2={3,7,13,…,p2}.

图1次要用户的交会示意图

Fig.1Schematic diagram of rendezvous of SUs

(1)

(2)

2.3算法正确性与性能评估

为证明AMCH算法的正确性,文中提出了定理2.

TTR是反映交会跳频算法性能的重要指标.常用最大交会时间(MTTR)与平均交会时间(ATTR)来评估TTR.MTTR是SU之间交会所用时隙数的最大值,ATTR是这些时隙数的平均值.文献[10-12]中的交会跳频算法与AMCH算法的MTTR与ATTR比较如表1所示,其中g为SUa与SUb的共同信道数,pH为SRB算法中接收机的跳频概率.

表1　几种交会跳频算法的最大交会时间和平均交会时间

3仿真结果与分析

认知网络中的授权信道数N=100.SU分布于PU周围,PU随机占用C中的信道,假设在一段时间内PU的占用率为θ并保持不变.随机选择两个SU作为发射机与接收机,用Matlab对4种跳频交会算法进行仿真,每种算法运行1000次,选择最大的TTR作为MTTR,TTR的平均值作为ATTR.

当PU的占用率θ=0.2、SU的可用信道数为80、SUa与SUb的共同信道数g∈[30,40],或者增大PU的占用率使θ=0.5、SU的可用信道数变为50、保持SUa与SUb的共同信道数不变时,4种算法的MTTR和ATTR如图2所示.

图24种算法的MTTR 和ATTR比较

Fig.2Comparison of MTTR and ATTR among four algorithms

从图2(a)可知:ACH、ARCH与AMCH算法的MTTR随着共同信道数g的增加而减小,这说明共同信道数越多,SU之间的交会发生得越快(交会时间越小);AMCH算法的MTTR明显小于其他算法;当减少SU的可用信道数时,ACH、ARCH算法的MTTR几乎没有改变,说明这两种算法的MTTR与授权信道数和共同信道数有关,而AMCH和SRB算法的MTTR显著减小,尤其是θ=0.5时,说明这两种算法的MTTR(交会时间上限)与SU的可用信道数正相关.SU的可用信道数越少,SU的交会就会发生得越快.SRB算法使SU的交会受到PU随机占用活动的影响.一些情况下,接收机停留在某些信道上(非共同信道)将造成SU长时间无法交会.从图2(a)还可以看出,由于随机因素的影响,SRB算法的MTTR曲线波动较其他算法大,而AMCH算法却能最大程度地利用可用信道集设计跳频序列,通过减小跳频序列冗余提高交会效率,由此获得最小的MTTR.

由图2(b)可以看出,AMCH与SRB算法的ATTR优于其他两种算法,这与图2(a)中MTTR的情况是一致的.AMCH与SRB算法的ATTR之间差距并不显著.虽然SRB算法交会的效率较高,但少数情况下其TTR仍然很大.综合来说,AMCH与SRB算法的ATTR比较接近,但AMCH算法的MTTR更小,因此AMCH算法优于SRB算法.通过上述分析可以发现,AMCH算法的TTR与可用信道数正相关,当SU的可用信道数与授权信道数接近时,AMCH算法的交会性能优势减小,当SU的可用信道数与授权信道数差异较大时,AMCH算法的优势将显现.

4结论

在认知网络中交会成为SU建立通信链路不可或缺的过程,而交会跳频算法具有性能稳定、协议开销较小等优势.针对认知网络中应用广泛的不对称模型,文中提出了一种可兼容支持一般的认知网络与异构认知网络的交会跳频算法AMCH.仿真实验结果表明,与现有算法相比,AMCH具有最短的交会时间.作为一种简单的跳频交会算法,AMCH没有涉及到接收机和发射机的协调机制.今后将考虑加入协调机制，使AMCH更加完善.

参考文献：

[1]Wang Peng,Xiao Li-min,Zhou Shi-dong,et al.Optimization of detection time for channel efficiency in cognitive radio systems [C]∥Proceedings of 2007 Wireless Communications and Networking Conference.Kowloon:IEEE,2007:111-115.

[2]Mitola J,Jr Maguire G Q.Cognitive radio:making software radio more personal [J].IEEE Personal Communications,1999,6(4):13-18.

[3]Akyildiz I F,Lee Won-yeol,Vuran M C,et al.A survey on spectrum management in cognitive radio networks [J].IEEE Communications Magazine,2008,46(4):40-48.

[4]AkyildizvI F,Lee Won-yeol,Roy-Chowdhury A K.CRAHNs:cognitive ad hoc networks [J].Ad Hoc Networks,2009,7(5):810-836.

[5]Alpern S,Gal S.The theory of search game and rendezvous [M].New York:Springer-Verlag,2003:165-177.

[6]Liu Si-si,Loukas Lazos,Krunz M.Cluster-based control

channel allocation in opportunistic cognitive radio networks [J].IEEE Transactions on Mobile Computing,2012,11(10):1436-1449.

[7]Li Xiao-Yan,Hu Fei,Zhang Hai-Lin,et al.A cluster-based MAC protocol for cognitive radio ad hoc networks [J].Wireless Personal Communications,2013,69(2):937-955.

[8]Chuang I-Hsun,Wu Hsiao-Yun,Kuo Yau-Hwang.A fast blind rendezvous method by alternate hop-and-wait channel hopping in cognitive radio networks [J].IEEE Trans-actions on Mobile Computing,2014,13(10):2171-2184.

[9]Wu Shan-Hung,Wu Ching-Chan,Hon Wing-Kai,et al.Rendezvous for heterogeneous spectrum-agile devices [C]∥Proceedings of 2014 International Conference on Computer Communications.Toronto:IEEE,2011:2247-2255.

[10]Bian Kaigui,Park Jung-Min.Maximizing rendezvous diversity in rendezvous protocols for decentralized cognitive radio networks [J].IEEE Transactions on Mobile Computing,2013,12(7):1294-1307.

[11]Chang Guey-Yun,Teng Wen-Hung,Chen Hao-Yu,et al.Novel channel-hopping schemes for cognitive radio networks [J].IEEE Transactions on Mobile Computing,2014,13(2):407-421.

[12]Guerra E O,Reguera V A,Souza R D,et al.Simple role-based rendezvous algorithm for cognitive ad hoc radio networks [J].IEEE Electronics Letters,2014,50(3):182-184.

[13]Lo B F.A survey of common control channel design in cognitive radio networks [J].Physical Communication,2014,4(1):26-39.

[14]Cormio C,Chowdhury K R.A survey on MAC protocols for cognitive radio networks [J].Ad Hoc Networks,2009,7(7):1315-1329.

[15]Yang D,Shin J,Kim C.Deterministic rendezvous scheme in multi-channel access networks [J].IEEE Communications Letters,2010,46(20):1402-1404.

Channel-Hopping Algorithm for Rendezvous Based on

Asymmetric Model in Cognitive Networks

ZhongMingZhangHai-linMaBeiLanBing

(School of Telecommunications Engineering，Xidian University，Xi’an 710071,Shaanxi，China)

Abstract:Proposed in this paper is a novel channel-hopping algorithm for rendezvous on the basis of asymmetric model in cognitive networks (named AMCH). According to the available channel set sensed by each secondary user, the lengths of channel hopping sequences for transmitters and receivers are selected in two disjoint sets of prime numbers, and two channel hopping sequences are respectively constructed. Without any other auxiliary information (such as the synchronization information and the global channel label information, etc.), any two secondary users within the communication scope can rendezvous in a short time and establish a link in their common channels. In comparison with the existing algorithms, AMCH algorithm diminishes the redundancies of channel-hopping sequences and improves the efficiency of rendezvous. Simulated results show that AMCH algorithm outperforms the existing algorithms in terms of time-to-rendezvous upper boundary and rendezvous performance.

Key words: cognitive radio;cognitive radio networks;asymmetric model;channel-hopping algorithm;rendezvous