识别几何图形“六要”
□陈德前
识别几何图形“六要”
□陈德前

初学平面几何,学会识别几何图形是一项基本功.许多初学几何者往往对识别几何图形不够重视,从而影响到整个平面几何的学习.那么,怎样学会识别平面几何图形呢?
一、要全面识别几何图形
如图1,从和的角度来看,两条线段合起来就是整条线段,即有AC=AB+BC;从差的角度来看,AB或BC是两条线段的差,从而有AB=AC-BC,BC=AC-AB.

图1
二、要从不同的角度识别几何图形
同一个图形,从不同的角度来看,则会得到不同的结论,如图2就可以有若干种不同的说法.
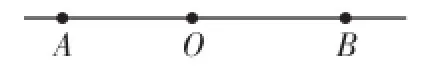
图2
例如,它表明:
1.直线AB经过点O;
2.点B在射线OA的反向延长线上;
3.∠AOB是以点O为顶点,OA、OB为边的一个平角;
4.A、O、B三点在一条直线上.
三、要把几何图形看“活”
如图3,若把点Q看“活”,易知它扮演了不同的角色:

图3
1.点Q在线段PR上,常称为线段PR的内分点(同样称P点或R点分别为线段QR和线段PQ的外分点);
2.特殊情况下,当PQ=QR时,点Q是线段PR的中点;
3.当点Q与点P或点R重合时,点Q又可以看作线段PR的端点.
四、要按一定的顺序识别几何图形
有些图形比较复杂,学会按顺序识别图形,可以避免重复或遗漏.如图4,直线l上有多少条线段?以A为顶点的角有几个?图中的三角形有几个?
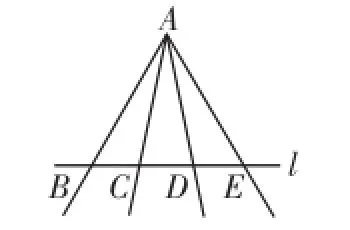
图4
遇到这类问题,可按照从左到右的顺序去识别:(1)以B点为左端点的线段有3条,以C点为左端点的线段有2条,以D点为左端点的线段有1条,故共有6条线段;(2)按逆时针方向,以射线AB为始边的角有3个,以射线AC为始边的角有2个,以射线AD为始边的角有1个,这样以A为顶点的角有6个;(3)以线段A为一边的三角形有3个,以线段A为一边的三角形有2个,以线段A为一边的三角形有1个,这样图中的三角形有6个.
如果按照从右到左的顺序去识别,同样可以得到上述结论,同学们不妨试一试.可见顺序识图法是解决几何识图问题的有效方法之一同学们要切实掌握,灵活应用.
五、要用准确的几何语言表示图形
几何语言与代数语言有所不同,必须在开始学习时就加以注意做到准确无误.除了听老师叙述外,同学们在看书时也应特别注意要弄清每一句术语的含义,并有意识地加以应用.例如,图5中的两个图形,第(1)个图形应叙述为“延长线段AB到C”,而第(2)个图形应叙述为“延长线段BA到C”或“反向延长线段AB到C”,其区别就在于是向哪一个方向延长的,延长AB就是由A到B的方向延长,而延长BA则是由B到A的方向延长,显然,两者是“背道而驰”的.再如,图6的两个图形,第(1)个图形应叙述为“两条线段AB与CD互相平分于点O”,第(2)个图形应叙述为“线段AB被线段CD平分于点O”.它们表面上相近,都有“平分”二字,但实质上有很大的差别,前者是互相平分,即A平分CD,CD也平分AB;而后者是CD平分AB,但AB没有平分CD.因此,老师经常要求同学们要看清题目(包括图形),在平面几何中,就是要细细体会每一句话,每一个词的含义,注意几何语言表达上的微小差别.
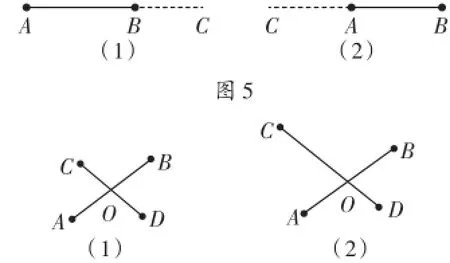
图6
六、要学会用几何语言说理
如图7,“因为AM=MB,所以M是线段AB的中点”;反之,“因为M是线段AB的中点,所以AM=MB”.同学们要学会应用这种形式来说理.
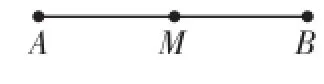
图7
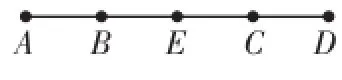
图8
例1如图8,点A、B、E、C、D在同一直线上,且AC=BD,E是BC的中点,那么点E是AD的中点吗?为什么?
分析:要说明E是AD的中点(图形位置),只要说明AE=ED(等量关系)即可.
解:点E是AD的中点.理由如下:因为点A、B、E、C、D在同一直线上,且AC=BD,所以AC-BC=BD-BC,即AB=CD.又因为E是BC的中点,所以BE=CE.所以AB+BE=CD+CE,即AE=ED,所以E是AD的中点.
例2如图9,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=21°,求∠AOB的度数.
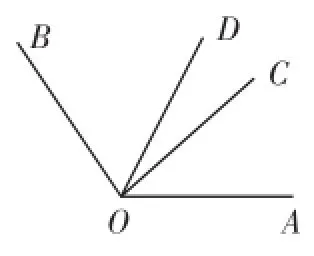
图9
°,则可列出方程求解.
我们要善于利用中点或角平分线的概念进行图形位置与度量关系的相互转换,进而去解决有关问题,这是学习几何的基本功,每一个同学都应该练好这个基本功,才能顺利通过几何入门关.

