基于ANSYS的组合荷载作用下水平受荷桩的有限元分析
李平均, 郭小刚, 傅文桥
基于ANSYS的组合荷载作用下水平受荷桩的有限元分析
李平均, 郭小刚, 傅文桥
(湘潭大学土木工程与力学学院, 湖南湘潭, 411105)
根据泰州市郊某一拟建工程中桩的水平静载试验数据, 运用有限元分析软件ANSYS, 对水平荷载单独作用下的单桩进行了三维有限元数值模拟与分析, 并在此基础上对模型进行改进, 研究了组合荷载作用下桩的工作性状。主要分析了水平荷载、轴向荷载、桩的抗弯刚度、桩径以及自由段桩长对桩身响应的影响。研究结果表明: 桩身水平位移和弯矩随着水平荷载和轴向荷载的增加而增大, 且当水平荷载较大时, 轴向荷载作用引起的–效应(轴向荷载引起的附加位移)比较明显, 其随自由段桩长的增加而增大, 随抗弯刚度和桩径的增加而减小。
水平荷载; 组合荷载; 桩; ANSYS
在港口、码头、大桥梁、海上油田开采平台、基坑开挖与支护、滑坡的防护等工程中, 桩基础[1]不仅要承受竖向荷载, 更多的还要承受较大的水平荷载、倾斜荷载[2–3]或力矩的作用。这种水平荷载和组合荷载[4–5], 对建筑物和基础都将产生不同程度的影响, 如四川省渡口铁路支线103站大滑坡问题, 采用65根抗滑桩并设置相配套的排水沟、盲沟、支撑渗沟等防护措施, 才将滑坡问题解决。
目前, 国内外关于桩的研究, 一般是将水平荷载和轴向荷载分开单独研究, 对承受水平荷载[6–9]和轴向荷载共同作用桩的研究还比较少。因此, 研究组合荷载作用下桩的工作性状具有非常重要的实际意义。本文采用有限元软件ANSYS对承受组合荷载作用的桩基础[10–11]的工作性状进行研究。根据泰州市郊某一拟建工程中桩的水平静载试验数据进行模拟并验证模型的正确性, 再在此基础上对模型改进, 研究组合荷载作用下桩的工作性状。主要分析了水平荷载、轴向荷载、桩的抗弯刚度、桩径以及自由段桩长对桩身响应的影响, 得到了一些有用的结论。
1 有限元模型的建立
拟建工程桩土的具体参数见表1、表2。考虑桩在实际工程中的受力情况以及为了节省计算时间, 采用对称桩—土模型。桩土模型参数的选取与实际工程的参数一致, 土体宽度取桩径的20倍, 桩体和土体均采用3D实体单元SOLID45, 桩—土接触单元选用CONTA173和TARGE170, 土体的非线性采用ANSYS自带的D–P模型[12–13]。在计算中, 桩底按照固定端考虑。

表1 桩参数
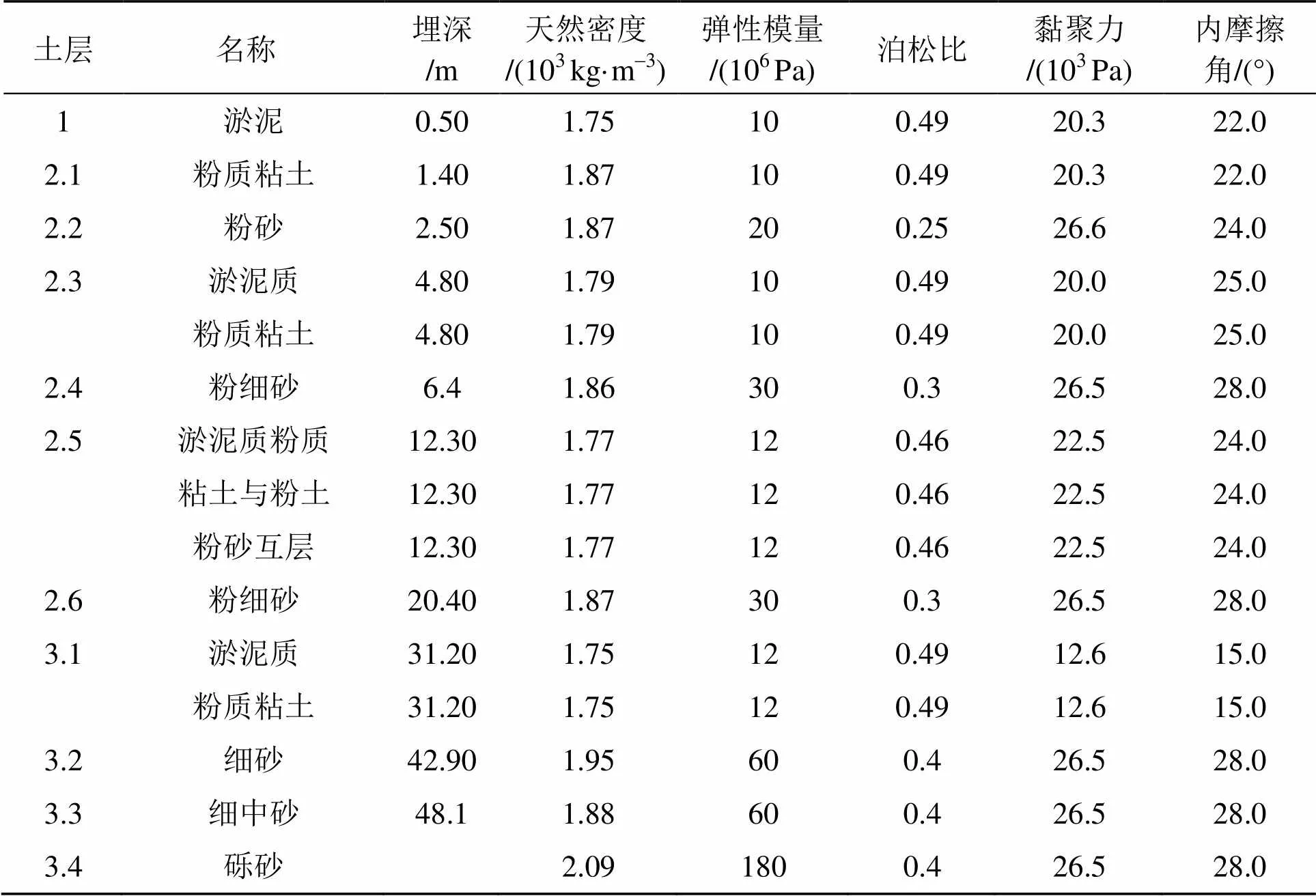
表2 地基土参数
计算模型如图1所示。本文采用的是不相关联的流动法则, 剪胀角取值为0, 摩擦系数取0.25,少数其他参数取经验值。

图1 桩—土计算模型
2 计算结果与分析
2.1 ANSYS模型的正确性验证
为了分析不同水平荷载作用下桩顶水平位移的变化情况, 在桩顶施加固定的竖向荷载和弯矩, 水平荷载的施加采用线性增加方式。桩顶水平位移模拟结果与试验数据对比如图2所示。

图2 水平荷载作用下, 桩顶位移实测与模拟值对比
从图2可知, ANSYS有限元模拟的桩顶水平位移结果与现场水平静载试验结果吻合得非常好。在不大的水平荷载作用下(<120 kN), 随着荷载增加, 桩顶的水平位移缓慢增加; 在较大水平荷载作用下(>120 kN), 桩顶的水平位移随荷载增加而加速增大, 说明桩体开始屈服。
2.2 水平荷载对桩的影响
2.2.1 水平荷载对无自由段桩的桩身弯矩的影响
在不同水平荷载作用下, 桩身弯矩响应曲线如图3所示, 图中为水平荷载(kN),为弯矩(kN·m), 下同。
由图3可知, 桩的弯矩随着水平荷载和弯矩的增加而增加, 且弯矩的增幅较大; 最大弯矩发生在距离桩顶(地面)10 m左右, 在距离桩顶43 m左右, 桩身开始出现很小的负弯矩; 由于土层的复杂性和轴向荷载的–效应, 桩身的弯矩响应随着埋深的增加呈现出非线性变化, 桩身最大弯矩发生在距离桩顶一定范围之内。
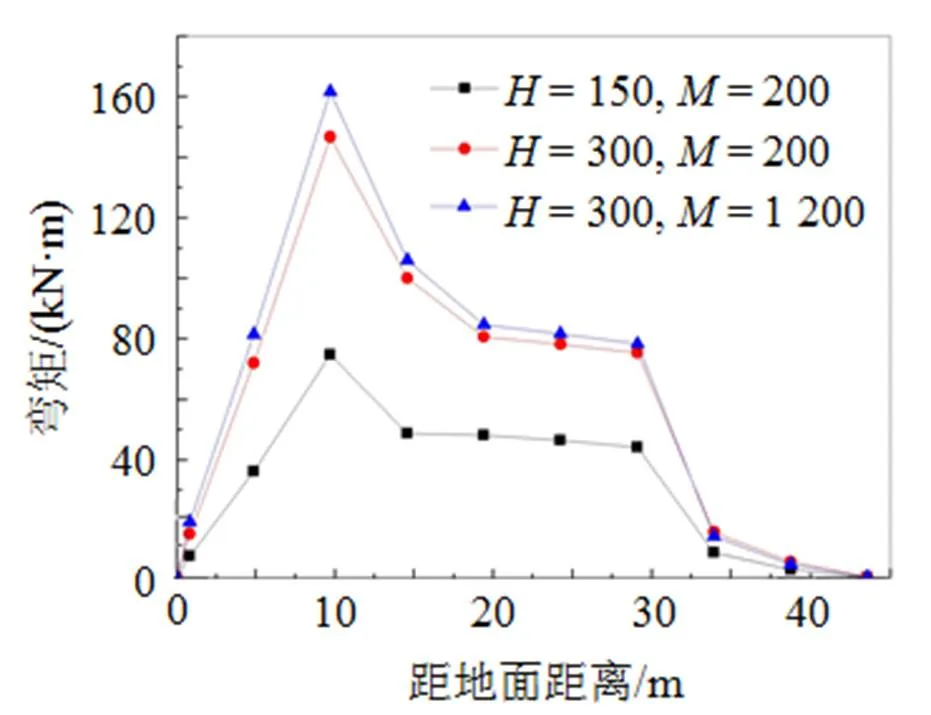
图3 水平荷载作用下, 无自由段桩长的桩身响应
2.2.2 水平荷载对有自由段桩的桩身弯矩的影响
在模型正确性被验证的基础上, 增加桩长使其伸出土体5 m, 研究水平荷载对有自由段桩的桩身弯矩的响应, 模拟结果如图4所示。
从图4可知, 当桩伸出土体一定的长度时, 桩身的弯矩响应相对于无自由段桩而言会有所不同, 这是因为荷载经过桩的自由段后再传递给地面以下桩, 其荷载作用和–效应都有所加强; 桩身最大弯矩发生在离桩顶15 m左右, 负弯矩出现在埋深37 m左右, 这与无自由段桩的模拟结果相比有所减小, 说明桩的有自由段对桩身弯矩产生了影响。同时, 桩在不同的荷载条件以及约束下, 都存在着一个临界桩长, 当桩长超过临界值时, 继续增加桩长对桩身响应的影响非常小。
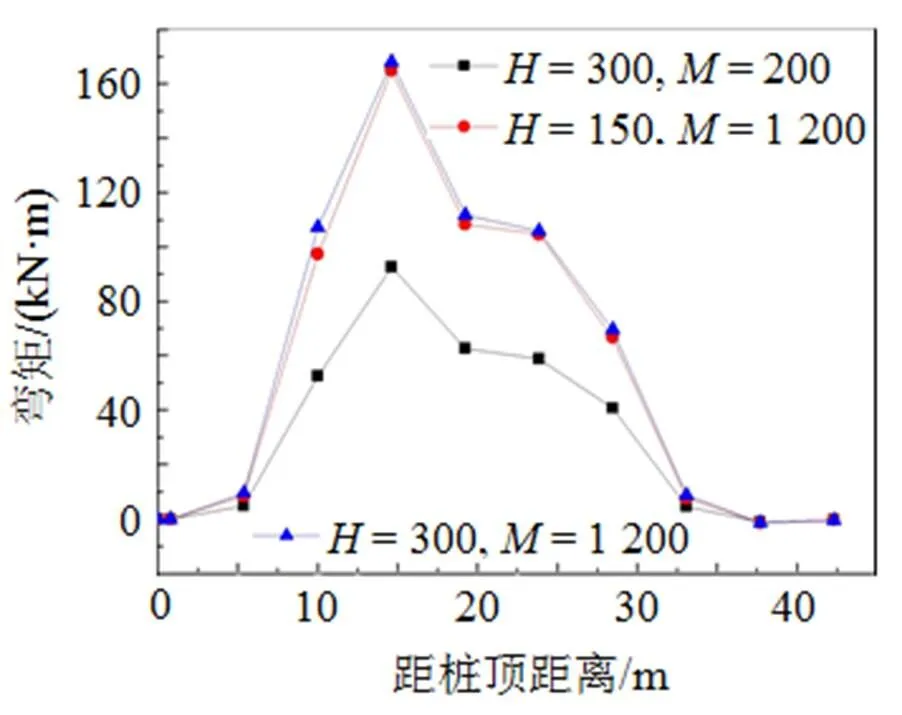
图4 水平荷载作用下, 有5 m自由段桩长的桩身响应
3 影响桩身响应因素分析
为进一步研究桩身水平位移和弯矩在不同影响因素条件下的响应, 在模型验证正确的基础上, 采用同样的建模方法对模型进行简化改进, 分析水平荷载、轴向荷载、桩的抗弯刚度、桩径以及自由段桩长度对桩身响应的影响。
入土桩长为30 m, 自由段桩长为15 m, 为简化计算, 自由段均布荷载取0, 忽略桩身自重轴向力对轴向荷载的影响。桩顶和桩底无约束, 均为自由端。简化模型参数见表3和表4, 简化模型如图5所示。

图5 桩土简化模型

表3 桩参数

表4 地基土参数
3.1 水平荷载
在加载时, 首先增加一恒定的轴向荷载= 1 000 kN, 再考虑在桩顶自由及桩底铰接的条件下, 不同水平荷载对桩的水平位移沿桩身分布的影响, 结果如图6所示。
从图6可知, 桩身的水平位移随着水平荷载和弯矩的增加而增大, 且在桩顶处, 它的水平位移增大幅度最大。在桩底处, 由于桩底无约束处于自由状态, 故桩底出现了负位移, 但是桩底的位移增加幅度要比桩顶的小, 这是因为随着桩埋深的增加, 桩身土反力也增大。在相同水平荷载作用下, 增加弯矩, 桩身的水平位移增大幅度较小, 说明在假定桩和土体材料都是线性材料的条件下, 弯矩和轴向荷载作用产生的–效应对桩身位移有一定的影响, 故而桩身的水平位移响应与水平荷载属于非线性关系。

图6 水平荷载作用下桩身水平位移响应
3.2 轴向荷载
在桩顶和桩底自由的条件下, 桩顶水平位移、地面处桩身的水平位移以及桩身最大弯矩在不同水平荷载条件下与轴向荷载的关系, 分别如图7(a), (b), (c)所示, 桩身最大弯矩距离桩顶的距离和轴向荷载的关系如图8所示。


图8 桩身最大弯矩距桩顶距离与轴向荷载的关系
从7图可知, 在水平荷载不变的情况下, 桩顶水平位移、地面处桩身的水平位移和桩身最大弯矩都随着轴向荷载的增加而增大。当轴向荷载不大时, 其增加幅度不大, 轴向荷载引起的–效应不是很明显。随着轴向荷载的不断增加,–效应越来越明显, 桩顶水平位移、地面处桩身的水平位移和桩身最大弯矩的增加幅度越来越明显。从图7(a)中曲线后半段可知, 在水平荷载较大的情况下, 随着轴向荷载的增加, 桩身位移和最大弯矩的增速都有略微的加大趋势, 因此可以推测, 在水平荷载足够大及轴向荷载和自由段桩长都较大时,–效应不容忽视。
3.3 桩身抗弯刚度
在研究桩的抗弯刚度对桩身响应的影响时, 假定桩端承受水平力= 200 kN, 弯矩= 600 kN·m, 轴向荷载= 1 000 kN, 得到桩顶自由时桩顶水平位移、地面处桩身水平位移和桩身最大弯矩在不同水平荷载作用下的关系分别如图9(a), (b), (c)所示, 桩身最大弯矩距离桩顶的距离与水平荷载的关系如图10所示, 图中为抗弯刚度, 单位kN·m2,为桩直径, 单位m,下同。


图10 不同抗弯刚度下, 最大弯矩距桩顶距离随水平荷载的变化
从图9(a)和图9(b)可知, 桩顶水平位移和地面处桩身水平位移随着水平荷载的增加而增加, 随着桩的抗弯刚度的减小而增大, 这是因为桩的抗弯刚度越小, 桩抵抗侧向变形的能力就越弱, 水平位移就会越大。由图9(c)可知, 桩身最大弯矩随着桩的抗弯刚度的减小逐渐增大, 随着水平荷载的增加而增加, 从曲线后半段可以看出, 随着水平荷载的继续增加, 桩身最大弯矩的增大越来越明显。从图10可知, 桩身最大弯矩距离桩顶的距离随着桩的抗弯刚度的增大而增大, 这是因为抗弯刚度大, 导致桩身位移较小, 桩身土反力也较小。
3.4 桩直径
在研究不同直径桩对桩身响应的影响时, 假定桩端承受水平力= 200 kN, 弯矩= 600 kN·m, 轴向荷载= 1 000 kN, 得到桩顶自由时桩顶水平位移、地面处桩身水平位移和桩身最大弯矩在不同水平荷载作用下的关系分别如图11(a), (b), (c)所示, 桩身最大弯矩距离桩顶距离与水平荷载的关系如图12所示。
从图11可知, 桩顶水平位移和地面处桩身水平位移随着水平荷载的增加而增加, 随着桩直径的增加而减小, 且在桩直径为0.8 m时的水平位移比桩直径为1.6 m和2.4 m时要明显大很多, 这是因为其截面惯性矩较小, 桩的抗弯刚度较小, 这也证明了上面关于桩的抗弯刚度对桩身响应的影响的研究结果是正确的。桩径为1.6 m和2.4 m时桩身响应差别较小, 说明桩直径增大对桩身响应的影响不是很敏感。从图12可知, 最大弯矩距桩顶距离随着水平荷载的增加而略微减小, 而随着桩径的增大而增大。
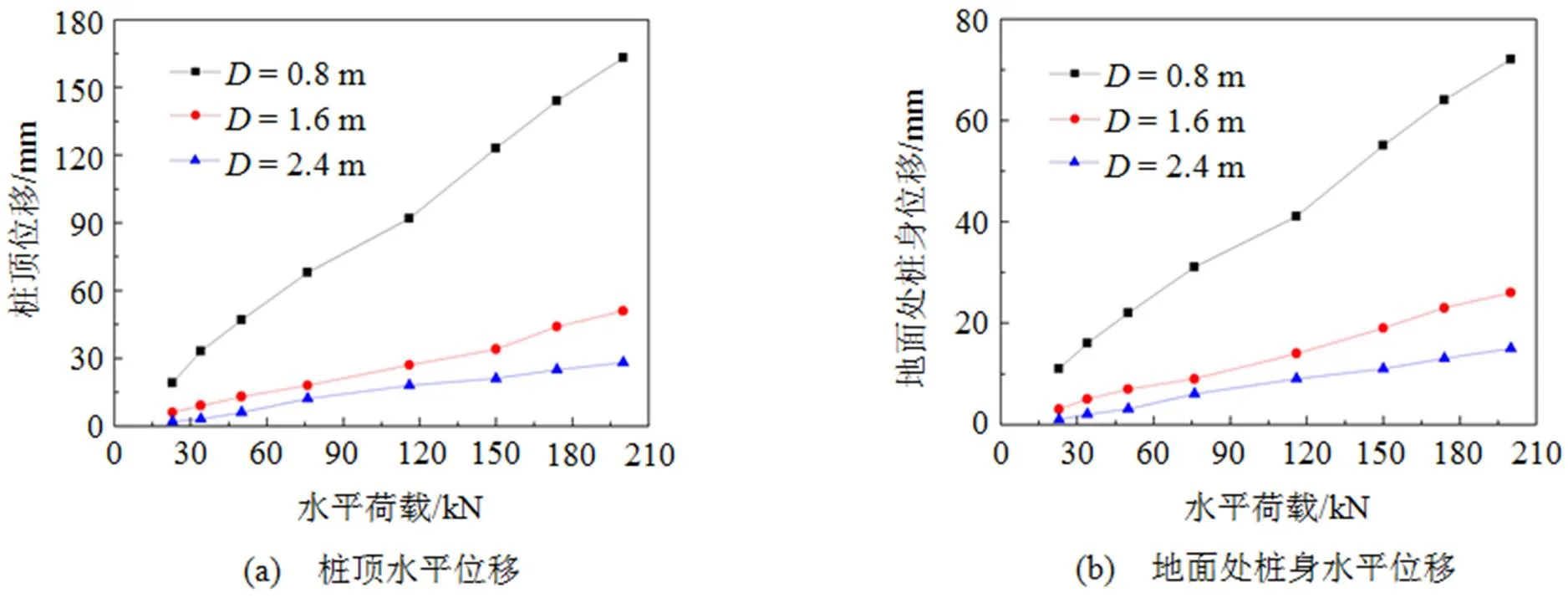

图12 不同桩径下, 最大弯矩距桩顶距离随水平荷载的变化
3.5 自由段桩长度
桩顶、桩底自由时, 桩顶水平位移、地面处桩身水平位移和桩身最大弯矩在不同水平荷载作用下与不同自由段桩长的关系分别如图13(a), (b), (c)所示; 桩身最大弯矩距地面处距离和自由段桩长的关系如图14所示。
从图13可知, 桩顶水平位移、地面处桩身水平位移和桩身最大弯矩随着自由段桩长的增加而快速增加, 主要原因是自由段桩长的增加, 轴向荷载作用引起的–效应加大, 从而导致地面以下桩身土反力的加大。从图14可知, 桩身最大弯矩距地面的距离随自由段桩长的增加而近似呈线性减小。


图14 不同荷载下, 最大弯矩距地面距离随自由段桩长的变化
4 结论
本文在对水平静载试验进行模拟验证的基础上, 利用ANSYS软件, 对桩土的相互作用进行了模拟分析。研究了水平荷载、轴向荷载、桩的抗弯刚度、桩径以及自由段桩长对桩身响应的影响, 所得结论如下:
(1) 桩基础存在一个桩长临界值和桩径最优值。当桩长增加到一定长度, 再增加桩长对桩的工作性状影响不大; 桩径有一个最佳桩径值, 增大桩径对于桩的水平承载能力影响不大。
(2) 桩身水平位移和弯矩响应随着水平荷载和轴向荷载的增加而增大, 且当水平荷载和轴向荷载较大时, 轴向荷载作用引起的–效应会越来越明显, 在桩基础设计中应当引起重视。
(3) 桩身水平位移和弯矩随自由段桩长的增加而增大, 最大弯矩距离地面的距离成线性减小; 桩身水平位移和弯矩随着桩抗弯刚度和桩径的增加而减小。
参考文献:
[1] 张忠苗. 桩基工程[M]. 北京: 中国建筑工业出版社, 2007.
[2] 郑刚, 王丽. 成层土中倾斜荷载作用下桩承载力有限元分析[J]. 岩土力学, 2009, 30(3): 680–687.
[3] 赵明华, 邹新军, 邹银生, 等. 倾斜荷载下基桩的改进有限元–有限层分析方法[J]. 工程力学, 2004, 21(3): 129–133.
[4] 柴红涛, 文松霖. 水平竖直组合荷载作用下桩基承载特性的离心模型试验研究[J]. 长江科学院院报, 2013, 30(12): 87–90, 96.
[5] 顾国锋, 赵春风, 李尚飞, 等. 沙土中组合荷载下单桩承载特性的室内模型试验研究[J]. 岩土工程学报, 2011, 33(Z2): 379–383.
[6] 刘汉龙, 陶学俊, 张建伟, 等. 水平荷载作用下PCC桩复合地基工作性状[J]. 岩土力学, 2010(9): 2 716–2 722.
[7] 庄培芝, 亓乐, 周志东. 水平荷载作用下单桩承载力影响因素分析[J]. 公路, 2013(8): 12–19.
[8] 杨建平, 朴春德, 常鸿飞, 等. 水平荷载下灌注桩变形分布式检测及承载机制研究[J]. 岩石力学与工程学报, 2014(Z1): 2 983–2 988.
[9] Karthigeyan S, Ramakrishna V V G S T, Rajagopal K. Influence of vertical load on the lateral response of piles insand [J]. Computers and Geotechnics, 2006, 33(2): 121–131.
[10] 郑刚, 王丽. 竖向及水平荷载加载水平、顺序对单桩承载力的影响[J]. 岩土工程学报, 2008(12): 1 796–1 804.
[11] 尹武先, 姚文娟, 程泽坤. 轴–横向荷载作用下超长桩数值模拟[J]. 水利水运工程学报, 2009(2): 15–20.
[12] 邓楚键, 何国杰, 郑颖人. 基于M–C准则的D–P系列准则在岩土工程中的应用研究[J]. 岩土工程学报, 2006, 28(6): 735–739.
[13] 杨强, 杨晓君, 陈新. 基于D–P准则的理想弹塑性本构关系积分研究[J]. 工程力学, 2005(4): 15–19, 47.
(责任编校: 江河)
Finite element analysis of piles with standing horizontal loads in complex foundation
Li Pingjun, Guo Xiaogang, Fu Wenqiao
(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)
According to the level of static load test data of pile, which from the proposed construction project of Taizhou suburb, the pile under horizontal load is analyzed in three-dimensional finite element numerical simulation by ANSYS, and the work character of pile under combined loads by the improved model is studied. The influence of the horizontal load, axial load, bending stiffness of pile, pile diameter and free period of pile length to the response of pile body is analyzed. The results show that: The horizontal displacement and bending moment of pile increase with the increasing of horizontal load and axial load, and the axial load effect of-(additional displacement caused by axial load) is obvious when the horizontal load is bigger, and it increases with the increasing of the free period of pile length, also it decreases with the increasing of bending stiffness and pile diameter.
horizontal load; combined load; pile; ANSYS
10.3969/j.issn.1672–6146.2015.03.014
TU 473
1672–6146(2015)03–0055–07
李平均, 493941619@qq.com。
2015–03–10

