BP神经网络改进遗传算法在桁架结构优化设计中的应用

李梦欢，徐　安

（广州大学广州大学－淡江大学工程结构灾害与控制联合研究中心，广东广州　510006）

BP神经网络改进遗传算法在桁架结构优化设计中的应用

李梦欢，徐安*

（广州大学广州大学－淡江大学工程结构灾害与控制联合研究中心，广东广州510006）

遗传算法直接应用于结构优化设计时，需要对每代进化种群的全部个体进行结构有限元分析，这将耗费大量的计算时长.文章针对这一问题，首先采集若干组进行结构有限元分析的数据样本，并代入BP神经网络进行网络训练和仿真，然后在运用优化算法进行优化迭代运算时，回避大量个体的有限元重分析过程，而代之以BP神经网络的预测结果，从而大量节省了计算时间.17杆平面桁架结构和42杆空间结构的算例表明，采用本文方法的计算耗时分别比原始的遗传算法节省80.39％和83.21％，且优化迭代过程能够稳定收敛，从而验证了本文方法的有效性.

遗传算法；BP神经网络；结构优化；桁架结构

工程结构优化设计，就是在满足某种特定要求状态下，使结构重量、造价等指标达到最佳，更好的发挥投资效益.桁架结构在工程中应用是非常广泛的，且大型、复杂的桁架结构体系日益增多，在工程实践中如何满足设计条件下工程实际需要，对其进行结构优化设计是一个非常有意义且值得研究的问题.

遗传算法［1］作为一种典型的智能型算法，被广泛应用于解决结构优化问题.遗传算法具有良好的全局搜索能力，搜索过程中不受问题的内在因素、复杂程度、领域所限制，且不受目标函数和约束条件所限制，有很好的实用性和扩展性.但是也有其缺点［2］，如局部搜索能力较差、易陷入早熟和不能够及时利用反馈信息，导致搜索速度变慢等.遗传算法应用于结构优化设计的主要问题，在于每一代进化的种群个体均需要代入有限元模型进行结构重分析，这是非常耗时的，尽管PAN［3］、HAGEMAN［4］及朱灿等［5］对算法做了大量的改进，问题依然存在.从本文后面的算例可以看到，即便是只有17根杆件的简单平面桁架结构，如果运用原始的遗传算法进行优化迭代运算，需耗时500min以上，对于更为复杂的结构，过长的耗时通常是难以被工程师接受.

为了在实际结构中更好的应用结构优化技术，除了建立合理可靠的结构模型外，还须选择收敛效果好且适应于复杂结构的优化算法.针对这一问题，本文引入BP神经网络，回避了对于单个个体频繁的结构重分析过程，选用特定的随机个体先训练BP网络，然后在进行优化迭代运算时，直接调用BP网络预测结果，这样大大提高了运算效率，减少了计算耗时.

1　理念与方法

1.1桁架结构设计的数学模型

结构体系每一根杆件均采用相同材料.弹性模量E、杆件密度ρ，最大允许位移以及荷载工况均已知.结构优化设计的数学模型见公式（1）～（6）.

式中W为目标函数，即桁架的总重量.n为桁架结构杆件总数，Ai（Di，ti）为第i根杆件的外直径和壁厚对应的截面设计变量，它是钢管截面直径Di和壁厚ti的函数；gj（x）为第j组截面设计变量的位移约束条件；式（5）是惩罚函数［6］，λ为惩罚因子，当求解变量满足一定条件时取1，不满足时取－1；Lj（x）为迭代次数关于截面面积的相关函数；R是人为设定的一个大数.在结构优化过程中为避免提早进入局部最优，或避免BP神经网络在结合遗传算法的情况下直接求解的困难，这里分两阶段进行，第一阶段在满足条件下用BP神经网络预测数据使约束条件达到一定范围寻得最优解，直到满足优化条件；第二阶段进行结构有限元模型计算并代入式（4）中进行约束验算，当满足式（5）中条件指标时，搜索结束；如果不满足继续回到第二阶段搜索，直到找到满足约束条件及迭代条件的设定.

1.2优化算法的选用

在结构优化中，关于截面尺寸优化，有很多算法，如满应力准则及二次规划等算法，都可以很好地完成优化.但不是所有的算法都能很好地适应结构的优化计算，这也使得我们不得不克服一些优化算法的缺陷，改进优化模型以及算法程序.本文采用遗传算法作为结构计算的基本算法.遗传算法具有很好的通用性，在实际工程中，只需要给出各参数变化范围及步长信息，就能对离散变量进行很好的处理；使用随机概率体系进行迭代，能够很好地结合其他算法，体现出很强的适用性和兼容性.因此适合结构优化程序计算，能够很好地体现智能分析的效果.

BP神经网络与遗传算法结合，可以避免陷入局部最优解的缺陷［7］，近几年来被广泛地用于其他领域以及简单的结构数据预测当中，如方峻、万晋及刘明贵［8－10］等均已验证结构优化计算可以达到设定误差和减少一定耗时，结果满足工程设计的需要.BP神经网络结构简单，可调整的参数多，便于操作选择，可以充分逼近任意复杂的非线性关系寻得最优解；可以自适应存储和反馈网络信息，创建一个针对某问题而设计的网络，发挥其高效精准的预测能力.图1中，500组数据中，70％用于训练网络，30％用于仿真模拟，仿真误差可以达到设定范围，有限元模型计算与BP神经网络预测数据几乎吻合；图2中，17杆平面桁架BP神经网络预测三维效果图，可见曲面均匀，无峰值，符合位移随外直径与壁厚的变化趋势，基本符合实际，说明采用BP神经网络可以很好地预测结构位移值，并应用于实际优化算法中.根据上述理论，桁架结构优化的算法流程见图3.

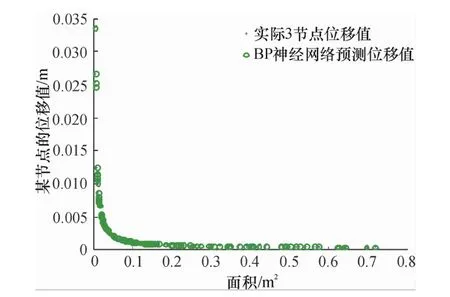
图1　42杆空间桁架结构数据比较Fig.1　Data comparison for the 42-bar spatial truss structure

图2　17杆平面桁架结构数据三维图Fig.2　Three-dimensional map data for the 17-bar plannar truss structure

图3　结构优化流程图Fig.3　The optimization process of structure

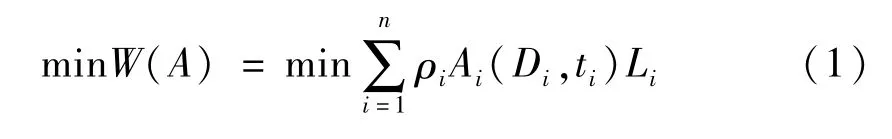
2　算例

下面对2个算例进行优化设计.

算例1

假设材料弹性模量E＝2.039×108kpa，密度ρ＝7 800kg·m－3，点3、4在水平和竖向方向上的容许位移为±0.04m.杆件的壁厚与外直径的下限为（Dmin，tmin）＝（0.04，0.01），其中在节点5处施加一个竖向荷载大小为444.8kN.模型见图4.

图4　17杆平面桁架结构Fig.4　The 17-bar plannar truss structure

（1）遗传算法参数设置：种群个体数100，迭代次数200，交叉、选择、变异概率分别为0.80、0.90、0.02；BP神经网络的参数设置：训练步长1 000次，训练速率0.02，误差目标为1×10－6，贝叶斯正则化训练函数等基本参数.

（2）本例仅以杆件的截面面积为变量进行截面优化.从图5～6中可见，在迭代到56代左右收敛，质量最优解为1 660.80kg，面积收敛结果为0.0042m2.从表1可见6次迭代平均误差7.5× 10－5，w1和w2分别表示3、4节点竖向位移绝对值，对比未利用BP神经网络及改进的优化程序，结构优化时间507.12min，优化后用时99.42min，这说明改进的优化计算有很好的收敛速度，计算时间节省了80.39％，很好地保证了时间效率和收敛性.

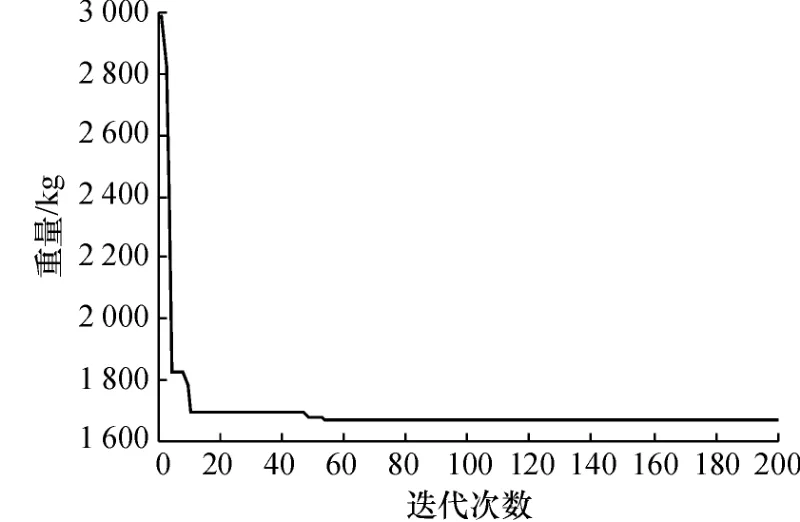
图5　17杆平面桁架结构质量收敛速度Fig.5　Weight of convergence rates for the 17-bar truss structure

图6　17杆平面桁架结构面积收敛速度Fig.6　Area of convergence rates for the 17-bar truss structure

表1　17杆平面桁架优化设计6次运行结果比较Table 1　Comparison of six optimal results for the 17-bar truss structure

算例2

假设材料均相同，材料弹性模量E＝2.58× 107kpa，密度ρ＝7 800 kg·m－3.点3、4在水平和竖向方向上的容许位移为±0.04m.杆件的外直径与壁厚的下限为（Dmin，tmin）＝（0.04，0.01），其中节点4、12水平荷载为22kN，竖向荷载为88.5kN，节点6、14只有竖向荷载88.5kN.模型见图7.min，这说明改进后的优化计算具有很好的收敛速度的效果，使计算时间节省83.21％，有效地保证了时间效率和收敛性.

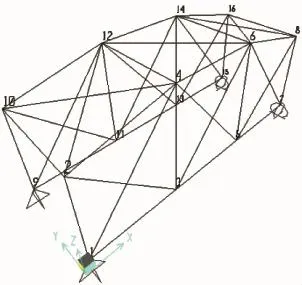
图7　42杆空间桁架结构Fig.7　The 42-bar spatial truss structure

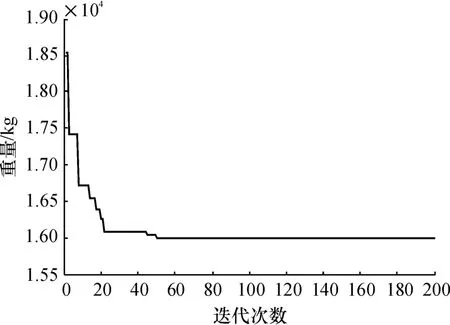
图8　42杆空间结构质量收敛速度Fig.8　Weight of convergence rates for the 42-bar spatial truss structure

（1）遗传算法参数设置：种群个体数100，迭代次数200，交叉、选择、变异概率分别为0.85、0.60、0.02；BP神经网络参数设置：学习次数1 000次，训练速率0.05，误差目标为1×10－6，贝叶斯正则化训练函数等基本参数.

（2）本例仅以杆件的截面面积为变量进行截面优化.从图8～9可见，在迭代到55代左右收敛，质量最优解为15 990.18kg，面积收敛结果为0.0033m2.从表2可见6次迭代平均误差为4.17 ×10－5，w1和w2分别表示3、4节点竖向位移绝对值，对比未利用BP神经网络及改进的优化程序，结构优化时间为590.84min，优化后用时101.50

图9　42杆空间结构面积收敛速度Fig.9　Area of convergence rates for the 42-bar spatial truss structure

表2　42杆空间桁架优化设计6次运行结果比较Table 2　Comparison of six optimal results for the 42-bar spatial truss structure

3　总　结

本文研究了BP神经网络改进遗传算法在桁架结构中的应用，利用BP神经网络精准预测结构约束值，再有效地结合遗传算法，汲取其优点回避其不足，从而节省了每一代种群个体有限元重分析所耗的大量时间，保证了很好的收敛结果.从给出的算例可见，17杆平面桁架和42杆空间桁架结构最优解分别为1 660.80kg和15 990.18kg，对比2种算法时间分别节省了80.39％和83.53％；BP神经网络对比有限元分析计算结果，平均误差分别为7.50×10－5和4.17×10－5.比较可知，精度满足工程优化设计需要，优化结果稳定收敛，节省了计算耗时.因此本文优化方法可行，并对大型复杂桁架结构的优化计算有一定的指导意义.

［1］HOLLAND JH.Adaptation in natural and artificial systems［M］.Cambridge：MIT Press，1975.

［2］玄光男［日］，程润伟.遗传算法与工程设计［M］.北京：科学出版社，2000.

XUAN G N［Japan］，CHENG RW.Genetic algorithms and engineering design［M］.Beijing：Science Press，2000.

［3］PAN Z J，KANG LS，NIE SX.Evolving both the topology and weights of neuralnetwork［J］.Parall Algor Appl，1996，9（3/4）：299-307.

［4］HAGEMAN JA，WEHRENSR，SPRANG H A van，etal.Hybrid genetic algorithm-tabu search approach for optimisingmultilayer optical coatings［J］.Analyt Chim Acta，2003，490（1/2）：211-222.

［5］朱灿，梁昔明，周书仁.基于物种选择的遗传算法［J］.小型微型计算机系统，2009，30（3）：534-536.

ZHU C，LIANG X M，ZHOU SR.Genetic algorithm based on species selection［J］.JChin Comput Syst，2009，30（3）：534-536.

［6］张晶，翟鹏程，张本源.惩罚函数法在遗传算法处理约束问题中的应用［J］.武汉理工大学学报，2002，24（2）：56-59.

ZHANG J，HUO P C，ZHANG B Y.Application of the penalty function combined genetic algorithm［J］.JWuhan Univ Tech，2002，24（2）：56-59.

［7］谢庆生，罗健，罗延科.机械工程中的神经网络方法［M］.北京：机械工业出版社，2003：100-104.

XIEQ S，LUO J，LUO Y K.Neural networksmethod ofmechanical engineering［M］.Beijing：China Machine Press，2003：100-104.

［8］方峻，李林林，徐诚.基于神经网络和遗传算法的身管多目标优化［J］.机械设计与制造，2013（8）：110-113.

FANG J，LIL L，XU C.Multi-objective optimization of barrel based on neural networks and genetic algorithms［J］.Mach Design Manuf，2013（8）：110-113.

［9］万晋，郑津.基于遗传算法和BP神经网络的圆柱壳大开孔接管结构优化研究［J］.福州大学学报：自科版，2014，42（5）：726-731.

WAN J，ZHENG J.Optimization of cylindrical shellwith large opening nozzle based on BP neural network and genetic algorithm［J］.JFuzhou Univ：Nat Sci Edi，2014，42（5）：726-731.

［10］刘明贵，杨永波.边坡位移预测组合灰色神经网络方法［J］.中国地质灾害与防治学报，2006，17（2）：74-78.

LIU M G，YANG Y B.Application of composite gray neural network method for prediction of slope displacement［J］.Chin J Geolog Hazard Contr，2006，17（2）：74-78.

Im proved genetic algorithm by BP neural network and its application in the optim ization of truss structures

LIMeng-huan，XU An

（Guangzhou University-Tamkang University Joint Research Center for Engineering Structure Disaster Prevention and Control，Guangzhou University，Guangzhou 510006，China）

The genetic algorithm is a commonly usedmethod for structural optimization.Thismethod requires to re-analyze the structure acted by loads for every individual in every evolution.Obviously this process is at a huge cost of computation.In this study，the BP neural network is employed tomodify this procedure.That is，some special training samples of structure are analyzed by the FEM software，and then，the results of nodal displacement are used to train the BP network.After that，in the evolution of a GA，re-analyzing of the structure is no longer required，and the structural displacements are predicted by the trained BP network.This procedure requiresmuch less computing time than the original GA.Two examples，including a 2D truss structure with 17 members and a 3D truss structure with 42 members are presented to show the validity of the proposed method.80.39％and 83.21％of computing time are saved by applying the proposed method，which demonstrates the validity of themethod.

genetic algorithm；BP neural network；structural optimization；truss structures

1671-4229（2015）06-0055-05

TU 323

A

2015－05－22；

2015－10－17

国家自然科学基金资助项目（51208127，51478130）；广州市科技计划资助项目（2014J4100141）

李梦欢（1991－），女，硕士研究生.E-mail：1335634376＠qq.com

.E-mail：44671105＠qq.com

【责任编辑：周全】