Analysis of Square-shaped Crack in Layered Halfspace Subject to Uniform Loading over Rectangular Surface Area

H.T.Xiao,Y.Y.Xieand Z.Q.Yue

Analysis of Square-shaped Crack in Layered Halfspace Subject to Uniform Loading over Rectangular Surface Area

H.T.Xiao1,2,3,Y.Y.Xie1,2and Z.Q.Yue4

This paper examines the problem of a square-shaped crack embedded in a layered half-space whose external surface is subject to a uniform loading over a rectangular area.Two novel numerical methods and the superposition principle in fracture mechanics are employed for the analysis of the crack problem.The numerical methods are based on the fundamental solution of a multilayered elastic medium and are,respectively,applied to calculate the stress fields of layered halfspace without cracks and the discontinuous displacements of crack surfaces in layered halfspace.The stress intensity factor(SIF)values are calculated using discontinuous displacements and the inf l uence of material properties and crack positions on the SIF values is analyzed.Using the minimum strain energy density criterion and the SIF values,the minimum values of the strain energy density factor arecalculatedandthecrackgrowthisanalyzed.Resultsshowthattheheterogeneity of layered media exerts an obvious inf l uence on the fracture properties of cracked layered elastic solids.

layered halfspace,square-shaped crack,stress intensity factors,crack growth,minimum strain energy density criterion,numerical methods.

1 Introduction

The study of the fracture mechanics of layered elastic solids has always occupied a prominent position in the literatures of solid mechanics.The crack problem in layered solids has applications to many problems of technological importance.Early studies of specific interests to fracture mechanics of layered elastic media were given by[Arin and Erdogan(1971)；Dhaliwal(1973)].In recent years,[Kuo and Keer(1995)；Bai and Pollard(1999)；Alaimo,Milazzo,Orlando(2013)；Zhang and Jeffrey(2006)]have developed various methods to analyze the crack problems in layered solids.[Dong and Atluri(2012,2013a,b)]has developed weaklysingular symmetric Galerkin boundary elements(SGBEM)and super elements for fatigue-growth analyses of cracks in stiffened panels with composite-patch repairs.[Dong and Atluri(2013c)]has further developed SGBEM voronoi cells for direct micromechanical numerical modeling of heterogeneous composites.It should be mentioned at this point that[Selvadurai(1998,2000)]developed boundary element techniques to analyze fracture evolution during indentation of a brittle halfspace and illustrated how the load-displacement exhibits a non-linear response due to the crack extension.The type of problems discussed in these developments largely focus on two-dimensional cracks[Chao and Wikarta(2012)]and some three-dimensional simple cracks such as penny-shaped cracks and elliptical cracks[Wang,Sun and Zhu(2011)].

Rectangularcracksareanothertypeofcracksthatarestudiedinfracturemechanics.But,because of their complex geometry,it is difficult to determine exact solutions of rectangular cracks.In some cases,rectangular cracks can be analyzed using numerical methods.[Weaver(1977)]utilized a system of integral equations for the analysis of rectangular cracks in an isotropic medium of infinite extent.[Murakami(1987)]presented the SIF values of rectangular cracks in an isotropic medium of semi-infinite extent under the action of remotely uniform stresses.[Bains(1992)；Bains,Aliabadi,and Rooke(1992)]presented a new procedure for the determination of the weight functions that are used to evaluate SIFs of a straight-fronted crack in a rectangular bar subjected to various loadings.[Pan and Yuan(2000)；Yue,Xiao and Pan(2007)]developed the dual BEMs to study rectangular cracks in a transversely isotropic material and a transversely isotropic bi-material,respectively.To the best of our knowledge,a literature review of the present study indicates that there are few publications in the open literature on a rectangular crack in a layered medium.

The purpose of this paper is to analyze a square crack problem in layered halfspaces subject to uniform rectangular loadings on the external surface,as shown in Fig.1.Two novel numerical methods and the superposition principle in fracture mechanics are employed.The proposed numerical methods are based on the fundamental solution in a multilayered elastic medium[Yue(1995)].The fundamental solution associated with concentrated body force vector used in this paper is also namedasYue’ssolutionby[Maloney,Walton,BruceandVanVliet(2008)].Forthe past 15 years,Yue’s solution has been used to develop the boundary element methods for the analysis of fracture mechanics in layered and graded solids[Xiao and Yue(2014)].Yue’s solution is also suitable for the layered media of semi-infinite extent.In an infinite layered medium,the elastic modulus of the upper semi-infinite medium is given an extremely small value,such as E0=1×10-10MPa and the Poisson’s ratio of the medium ν0=0.3.In this way,the fundamental solution of a layered medium of semi-infinite extent is obtained.Yue’s solution based numerical method is also used for the analysis of the contact problems involving the functionally graded materials[Xiao and Yue(2009)].

Figure 1:A square-shaped crack in a layered half-space subjected to uniform loadings on the boundary surface.

At first,the novel numerical methods are brief l y introduced and the superposition principle of fracture mechanics is presented for the analysis of the crack problems.In the ensuing numerical analyses,the stress fields of layered halfspaces without cracks are first obtained using a numerical method.The tractions on the crack surfaces are then prescribed according to the superposition principle and the discontinuous displacements on crack surfaces are finally calculated using another numerical method.The SIF values of square-shaped cracks in layered half-spaces are calculated using the discontinuous displacements on crack surfaces.Using the SIF values and the minimum strain energy density criterion,the minimum values of strain energy density factors around the crack tip are calculated and the crack growth is analyzed.Numerical results illustrate the inf l uence of the positions of the crack and the non-homogeneity of a layered medium on the fracture properties of cracked layered bodies.

2 Numericalmethodsforanalyzingthecrackprobleminalayeredhalf-space

2.1 Numerical method for elastic fields in a layered medium

Xiao,Yue and Zhao(2012)developed a numerical method for calculating elastic fi elds of a heterogeneous medium with depth using Yue’s solution.The stresses σij(Q)at any point Q of the layered medium are described as

The corresponding computer program LayerSmart3D was written in FORTRAN.The techniques adapted in LayerSmart3D primarily involve the discretization of the loading domain into a finite number of quadrilateral elements.Values of the loads are inputted at the node points of the discretized domain and the Gaussian numerical quadrature is used for obtaining the integral value on the element.Numerical verification of LayerSmart3D indicates that numerical solution of high accuracy can be efficiently calculated for elastic fields induced by the distributed loads in a layered medium.

2.2 DDM for analyzing crack problems in a layered medium

Xiao and Yue(2011)developed a new displacement discontinuity method(DDM)for the analysis of crack problems in layered strata of infinite extent.This approach is also based on Yue’s solution and the corresponding computer program LayerDDM3D was written in FORTRAN.

Assume that the crack surfaces consist ofIn global coordinatesthe discontinuous displacements of the crack surfaces are defined asis a displacement along the direction j=x,y,z.The traction on the crack surface is defined asThe basic equations of Yue’s solution based DDM are as follows

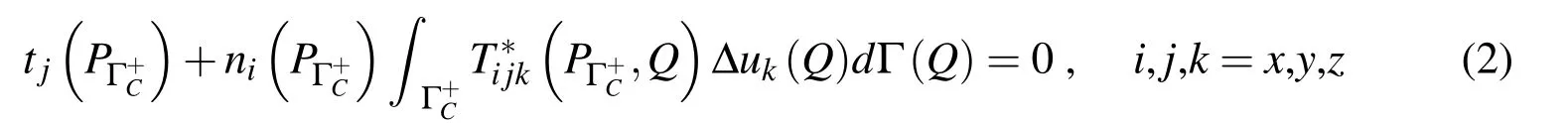
In developing the DDM for Eq(2),the nine-node continuous and discontinuous elements are used to discretize the crack surface.The Kutt’s numerical quadrature is used to calculate the hyper-singular integral in the discretized integral equation.By solving the discretized equations of Eq(2),the discontinuous displacements on the crack surface can be obtained.The numerical verification shows that the present results are in very good agreement with the existing ones.Notice that the proposed DDM is suitable only for the analysis of crack problems in layered media of infinite extent under the action of loadings on crack surfaces.

2.3 The superposition principle of fracture mechanics

Inthefollowings,theabove-mentionedtwonumericalmethods,i.e.,LayerSmart3D and LayerDDM3D,and the superposition principle in fracture mechanics are utilized to analyze crack problems in a layered medium.LayerSmart3D is employed to obtain the stress fields of a layered medium without a crack under the action of rectangular loadings on the boundary surface.Using the superposition principle in fracture mechanics,the tractions,which are equal to the stress calculated above and have opposite directions,are then loaded on the crack surfaces in the layered medium without rectangular loadings on the boundary surface.LayerDDM3D is employed to obtain the discontinuous displacements of the crack surfaces under the action of the above tractions.

3 Stress fields of a homogeneous halfspace without cracks

3.1 General

As shown in Figs.1 and 2,a square-shaped crack is located in a layered halfspace where a Cartesian coordinate system Oxyz is attached.The crack surfaces ΓCare parallel to the boundary surface z=0,have a vertical distance of h from the boundary and a horizontal distance of d from the coordinate plane Oyz.The loading area ΓLis a rectangular domain,has 2a wide and 3a long and is located at the boundary surface,i.e.,z=0.The side length of the square-shaped crack is 2a and a local Cartesian coordinate system O′x′y′is attached at the crack surface.A compressive load p is uniformly distributed on the area ΓL.

Under the action of the compressive load p,the shear stresses σxz,σyzand the compressive stress σzzare distributed on the non-crack area ΓC.According to the superpositionprincipleinfracturemechanics,thetractiononthecracksurface fz=-σzz,is tensile and makes the crack surfaces close.Thus,there is no mode I deformation and only mode II and III deformations exist.In the following,we discuss only the distribution of shear stresses σxzand σyzon the non-crack area ΓCin a homogeneous half-space without a crack.Assume that the elastic modulus is E and the Poisson’s ratio is 0.3 for a homogeneous half-space.

Figure 2:Loading area and crack surface on coordinate systems Oxyz and O′x′y′z′.

In order to calculate the stress fields using LayerSmart3D,the loading area ΓLis discretized into 150 8-noded elements and 501 nodes.The 441 calculating points arepositionedonthenon-crackareaΓCandcorrespondstothenodesoftheelement mesh on the square-shaped crack surfaces to be used in the following.

3.2 The shear stresses on the non-crack area ΓCin a homogenous half-space

3.2.1 The non-crack area ΓClocated directly below the loading area ΓL

In this case,the horizontal distance between the centers of the two areas ΓCand ΓLis equal to zero,i.e.,d=0.Figs.3 and 4 illustrate the distribution of the shear stresses σxzand σyzon the area ΓCfor h=0.2a.In Fig.3,σxzis symmetrical with respect to y′=0 and has maximum absolute values along x′/a= ±1 for different values.In Fig.4,σyzis symmetrical with respect to x′=0 and has maximum absolute values along y′/a= ±1 for different x′values.It can be also found that the maximum value of σyzis much larger than the one of σxzon the area ΓC.

Figs.5 and 6 show the variations of σxzalong y′=0 and σyzalong x′=0 on ΓCwith the depth h.In Fig.5,with the depth h increasing,the absolute value of σxzfirst increases,arrives at maximum values at about h/a=1 and then decreases and approaches an extremely small value near zero.In Fig.6,the variation of σyzwith h is much similar to the one of σxzwhilst the maximum values σyzappear at h/a=0.4-0.6.

3.2.2 The non-crack area ΓClocated at different positions along the x axis

Figure 3:The stress σxzon ΓCat d=0 and h=0.2a in a homogeneous half-space.

Figure 4:The stress σyzon ΓCat d=0 and h=0.2a in a homogeneous half-space.

Figure 5:Variations of σxzwith h along y′=0 in a homogeneous half-space.

Figure 6:Variations of σyzwith h along x′=0 in a homogeneous half-space.

Figure 7:Variations of σxzwith d(h/a=1 and y′/a=0)in a homogeneous halfspace.

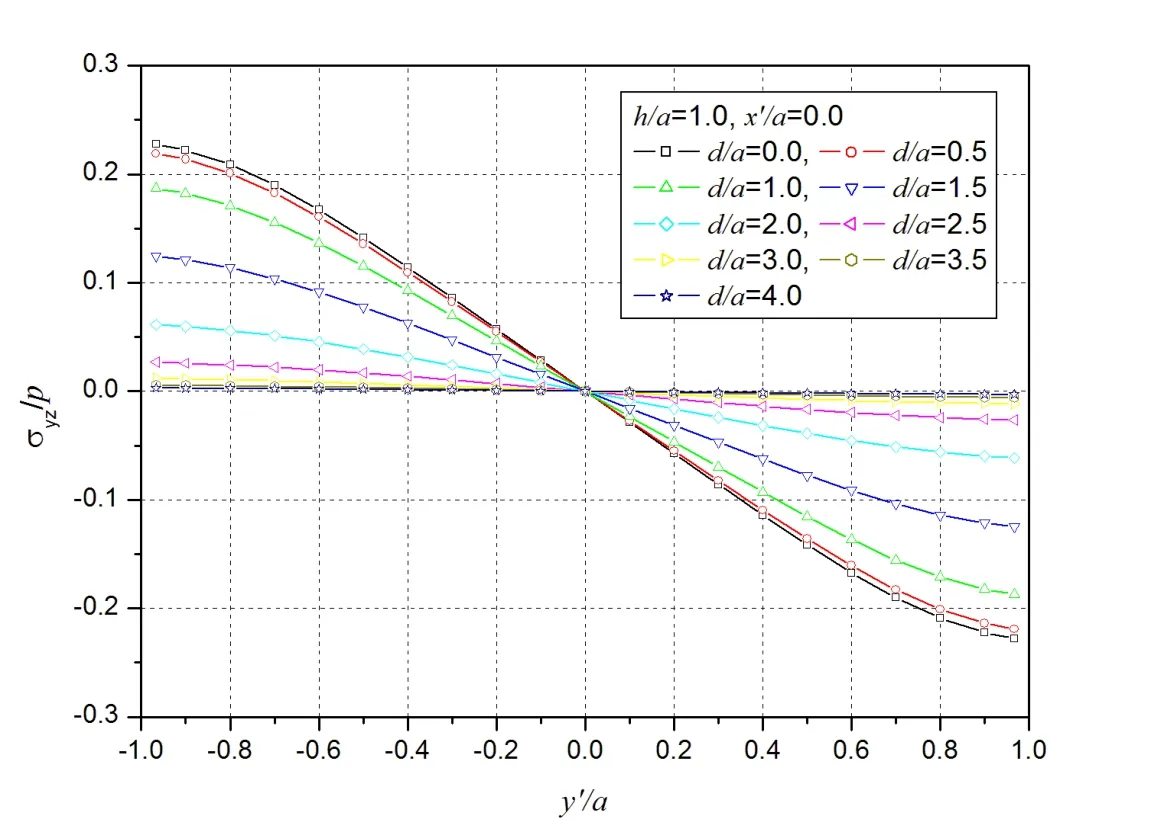
Figure 8:Variations of σyzwith d(h/a=1 and x′/a=0)in a homogeneous halfspace.

In this case,the area ΓCis located at the depth h/a=1 and has different horizontal distances d along the x axis.Figs.7 and 8 show the variations of σxzalong x′=0 and σyzalong y′=0 on ΓC.In the neighborhood of x′/a=-1,σxzfirst decreases,arrives at minimum values at d/a=3,then increase and approaches an extremely small value near zero with d increasing.In the neighborhood of x′/a=1,σxzfirst decreases,arrives at minimum values at d/a=1.5,then increase and approaches an extremely small value near zero with d increasing.In Fig.8,the absolute values of σyzdecrease as d increases.

4 Analytical methods of square-shaped cracks in layered media

4.1 General

The two cases are analyzed:Case 1:a square-shaped crack in a homogeneous half space,Case 2:a square-shaped crack in a layered half-space with two finite layers and a homogeneous halfspace.According to the superposition principle in fracture mechanics,the absolute values of the tractions on the crack surfaces in a layered half space without the surface force p are equal to the ones of the shear stresses on the area ΓCin a layered half-space without a crack whilst the directions of the tractions and the shear stresses are completely opposite.As shown in Fig.9,fx=-σxzand fy=-σyz.

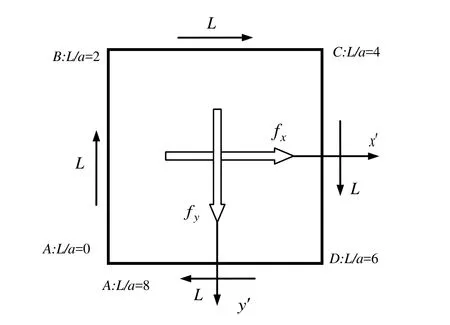
Figure 9:A square crack subjected to fxand fyand a moving local coordinate L attached at crack tip.

A square-shaped crack(the side length 2a)needs to be discretized to calculate the discontinuous displacements on the crack surfaces.[Xiao and Yue(2011)]analyzed the square crack in layered rocks and the mesh of the crack surface shown in Fig.6 of their paper can be further employed.One hundred(10×10)nine-node elements are used to discretize the crack surface.Among these elements,there are 64 nine-node isoparametric elements,32 discontinuous elements of type I,and four discontinuous elements of type II.The above-mentioned tractions are applied on 441 nodes of this element mesh.

4.2 Formulae of calculating SIF values

The SIF values can be calculated by using the discontinuous displacements.For the crack in multilayered solids but no located at the interface of two materials,the stress and displacement fields are the same as the ones of the crack in the homogenous solid.And the material parameters exert an inf l uence on the SIFs.Based on the relationship of displacements and the SIFs,the formulae of the SIFs are as follows

where(r,θ,φ)is the spherical coordinates located at the crack front.Note that Δux′or Δuy′are needed to calculate KIIand KIIIfor different sides of a square-shaped crack.

In order to plot the SIF values along the crack lines,a line coordinate Lshown in Fig.9 is attached at the crack front.The origin of the coordinate system is located at the corner A.L/a increases along the lines AB,BC,CD to DA.Correspondingly,L/a increases from 0-2,from 2-4,from 4-6,and from 6-8,respectively.

4.3 Analytical method of crack propagation

Growth of a crack in elastic solids subject to complex stress states can be assessed using the minimum strain energy density criterion(i.e.,S-criterion)proposed by[Sih(1973)；Sih and Cha(1974)].The S-criterion was developed on the basis of the strain energy density concept.It states that local instability is assumed to occur when the local minimum energy factor Sminreaches a critical value Scr.

Since only SIF values of modes II and III exist,the strain energy density factor S of a three-dimensional crack can be defined as[Hartranft and Sih(1997)]

where µ is the shear modulus of elasticity,ν is the Poisson’s ratio and θ is an angle in the coordinate plane normal to the crack line of crack front.

The direction of crack propagation should satisfy

According to Eq.(5),we have

In Eq.(6),it can found that the angle of crack propagation is only related to the Poisson’s ratio of the material where the crack is located.For ν =0.3,the angle of crack propagation θc= ±82.34o.Thus,substituting the SIF values obtained above and the propagation angle θcinto Eq.(5),the minimum energy factor Smincan be calculated.

5 Case 1:square-shaped crack in a homogeneous half-space

5.1 Case 1-1:The crack is located at the position with d=0 and different h values

5.1.1 SIF values of the crack

In this case,the crack is located directly below the loading area,i.e.,d=0.Figs.10 and 11 illustrate the variations of KIIand KIIIinduced by p with the depth h.Because of symmetry,only the SIF values along 0＜L/a＜4 are presented in these fi gures.As shown in Fig.10,except for h/a=0.1,the KIIvalues are negative along 0＜L/a＜2.At the depth h/a=0.1,the KIIvalues approach zero,are negative along a part of the crack front and positive along another part of the crack front.With the depth hincreasing,the absolute KIIvalues increase for 0.1≤h/a≤1 and decrease for h/a≥1.

InFig.11,KIIIispositivealong0＜L/a＜1andnegativealong1＜L/a＜2,andthe absolute values of KIIIare equal for two symmetric points with respect to L/a=1.With the depth h increasing,the absolute KIIIvalues increase for 0.1≤h/a≤0.6 and decrease for h/a≥0.6 along 0＜L/a＜2.KIIIis negative along 2＜L/a＜3 and positive along 3＜L/a＜4,and the absolute values of KIIIare equal for two symmetric points with respect to L/a=3.With the depth h increasing,the absolute KIIIvalues increase for 0.1≤h/a≤1.0 and decrease for h/a≥1.0 along 2＜L/a＜4.

Figure 10:Variations of KIIwith h for Case 1-1(d=0 and y=0).

Figure 11:Variations of KIIIwith h for Case 1-1(d=0 and y=0).

Figure 12:Variations of Sminwith h for Case 1-1(d=0 and y=0).

In summary,the absolute values of KIIand KIIIfirst increase and then decrease with the depth h increasing for a given distance d.This variation tendency is closely related to the distribution of fxand fywith the depth h,shown in Figs.5 and 6.

5.1.2 Analysis of crack growth

Fig.12 shows the variations of Sminalong the crack tips AB and BC using Eq.(5)and the SIF values presented in Figs.10 and 11.From this figure,we can have the following observations:

·Along the crack front AB,the values of Sminare symmetrical with respect to the central point L/a=1.At a given depth h,the maximum value of Sminappears between 0＜L/a＜0.5,for the value of KIIIarrives at the maximum value in this interval.As the depth h increases,the maximum value of Sminfi rst increases,arrives at the maximum value at h/a=0.6 and then decreases.When h/a=3,the maximum value of SminE/(p2a)is 0.4149×10-3.As the depth continues to increase,Sminapproaches zero.

·Along the crack front BC,the values of Sminare symmetrical with respect to the central point L/a=3.At most of given depths,the maximum values of Sminappear at the central point L/a=3,for the value of KIIarrives at the maximum value L/a=3.As the depth h increases,the maximum value of Sminfirst increases,arrives at the maximum value at h/a=0.6 and then decreases.When h/a=3,the maximum value of SminE/(p2a)is 0.4422×10-3.As the depth continues to increase,Sminapproaches zero.

·For a given depth,the maximum value of Sminalong the crack front AB and BC appears at the central point of the crack front BC.This means that if Smin=Scr,the crack growth initiates at the crack tip L/a=3.

5.2 Case 1-2:The crack is located at the positions with h/a=1 and different d values

5.2.1 SIF values of the crack

In this case,the crack is located at the depth h/a=1 and has different distances from the loading area along x-axis.Figs.13 and 14 illustrate the variations of KIIand KIIIwith the horizontal distance d.Because of symmetry,the absolute values of KIIand KIIIhave the same and their positive and negative symbols are completely opposite along 2＜L/a＜4 and 6＜L/a＜8.Thus,Figs.13 and 14 present only the SIF values along 0＜L/a＜6.

Figure 13:Variations of KIIwith d along x-axis for Case 1-2(h/a=1 and y=0).

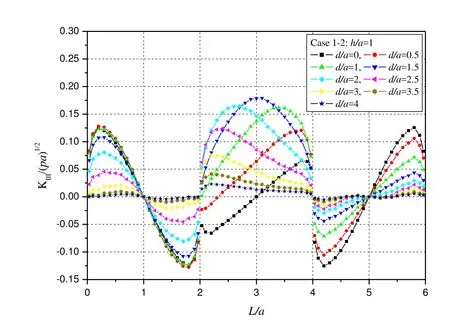
Figure 14:Variations of KIIIwith d along x-axis for Case 1-2(h/a=1 and y=0).

Figure 15:Variations of Sminwith d along x-axis for Case 1-2(h/a=1 and y=0).

In Fig.13,it can be found that KIIis symmetrical with respect to L/a=1 along 0＜L/a＜2.On the crack front of this side,KIIincreases for 0≤d/a≤2,decreases for d/a≥2.5 and approaches zero with the distance d increasing.Along 2≤d/a≤4,the KIIvalues are negative and are not symmetrical with respect to L/a=1.On the crack front of this side,the absolute values of KIIdecrease and approach zero with the distance d further increasing.Along 4≤L/a≤6,KIIis symmetrical with respect to L/a=5,the KIIvalues increases for 0≤d/a≤1 and decrease for d/a＞1 with the horizontal distance dfurther increasing.

In Fig.14,it can be found that KIIIis positive along 0＜L/a＜1 and negative along 1＜L/a＜2,and the absolute values of KIIIare equal for two symmetric points with respect to L/a=1.On the crack front of this side,the absolute values of KIIIincreases for 0≤d/a≤0.5,decreases for d/a＞0.5 and approaches zero with the distance d increasing.Along 2≤d/a≤4,the KIIIvalues are not symmetrical with respect to L/a=3.Along 2≤L/a≤3,the KIIIvalues increase for 0≤d/a≤1.5,and decrease and approach zero d/a＞2 with the distance d further increasing.Along 3＜L/a≤4,the KIIIvalues increase for 0≤d/a≤1.0,and decrease for d/a≥1.5 and approach zero with the distance d further increasing.Along 4≤L/a≤6,KIIIis negative along 4＜L/a＜5 and positive along 5＜L/a＜6,and the absolute values of KIIIare equal for two symmetric points with respect to L/a=5.On the crack front 4≤L/a≤6,and the absolute values of KIIIdecrease and approach zero with the distance d increasing.

In summary,the absolute values of KIIand KIIIfirst increase and then decrease with the distance d increasing for a given depth h.The variations of KIIand KIIIare closely related to the distribution of fxand fywith the distance d,shown in Figs.7 and 8.

5.2.2 Analysis of crack growth

Fig.15 shows the variations of Sminalong the crack tips AB,BC and CD using Eq.(4)and the SIF values presented in Figs.13 and 14.From this figure,we can have the following observations:

·Along the crack front AB,the values of Sminare symmetrical with respect to the central point L/a=1.For d/a=0,0.5,1,the maximum values of Sminappears between 0＜L/a＜0.5,for d/a=1.5 the maximum values of Sminappears at L/a=0.6 and for d/a=2-4 the maximum values of Sminappears at L/a=1.As the distance d increases,the maximum value of Sminfi rst increases,arrives at the maximum value at d/a=2 and then decreases.When d/a=4,the maximum value of SminE/(p2a)is 0.3193×10-3.As the distance continues to increase,Sminapproaches zero.

·Along the crack front BC,the values of Sminare not symmetrical with respect to the central point L/a=3 except for d/a=0.For d/a=0 the maximum values of Sminappears at L/a=3,for d/a=0.5,1 the maximum values of Sminappears between 3＜L/a＜4 and for d/a=1.5-4 the maximum values of Sminappears between 2＜L/a＜3.As the distance d increases,the maximum value of Sminfi rst increases,arrives at the maximum value at d/a=1.5 and then decreases.When d/a=4,the maximum value of SminE/(p2a)is 0.1098×10-3.As the distance continues to increase,Sminapproaches zero.

·Along the crack front CD,the values of Sminare symmetrical with respect to the central point L/a=5.For d/a=0 the maximum values of Sminappear at L/a=4.2,5.8 and for d/a=0-4 the maximum values of Sminappears at L/a=5.As the distance d increases,the maximum value of Sminif rst increases,arrives at the maximum value at d/a=1 and then decreases.When d/a=4,the maximum value of SminE/(p2a)is 0.2134×10-4.As the distance continues to increase,Sminapproaches zero.

·For different distances d,the maximum values of Sminappears at different crack fronts AB,BC and CD.This causes the crack growth fi rst initiates at different positions of the crack front for different distances d.

6 Case 2:square-shaped crack in a layered half-space

6.1 General

Fig.16 shows a square-shaped crack in a layered half-space with two finite layers and a homogeneous half-space.The thicknesses of the finite layers are a/2 and a.The elastic moduli of Materials 1 and 2 and the homogeneous half-space are E1,E2andE3,respectively.The Poisson’s ratios for three materials are 0.3.In the following,two cases,i.e.,E1=E3=2E2E1=E3=E2/2,will be discussed.The crack is located at Material 2 and is parallel to the boundary surface z=0.The above-mentioned mesh is further employed.

6.2 Case 2-1:E1=E3=2E2

6.2.1 SIF values of the crack

Figs.17 and 18 illustrate the variations of KIIand KIIIfor Case 2-1.From these fi gures,it can be found that the absolute values of KIIand KIIIfor a homogeneous medium are much larger than the ones for a layered half-space.This is because the elastic moduli of Materials 1 and 3 are larger than the ones of Material 2 and Materials 1 and 3 restrict the relative sliding of crack surfaces.As the depth h increases,the absolute values of KIIslightly increase along 0＜L/a＜2 and obviously decrease along 2＜L/a＜4.As the depth h increases,the absolute values of KIIIdecrease in the neighborhood of L/a=0.25 and L/a=1.75 and slightly increase along 2＜L/a＜4.

Figure 16:A square-shaped crack in a layered half-space consisting of two finite layers and a homogeneous half-space.

Figure 17:Variations of KIIwith h for Case 2-1(d=0).

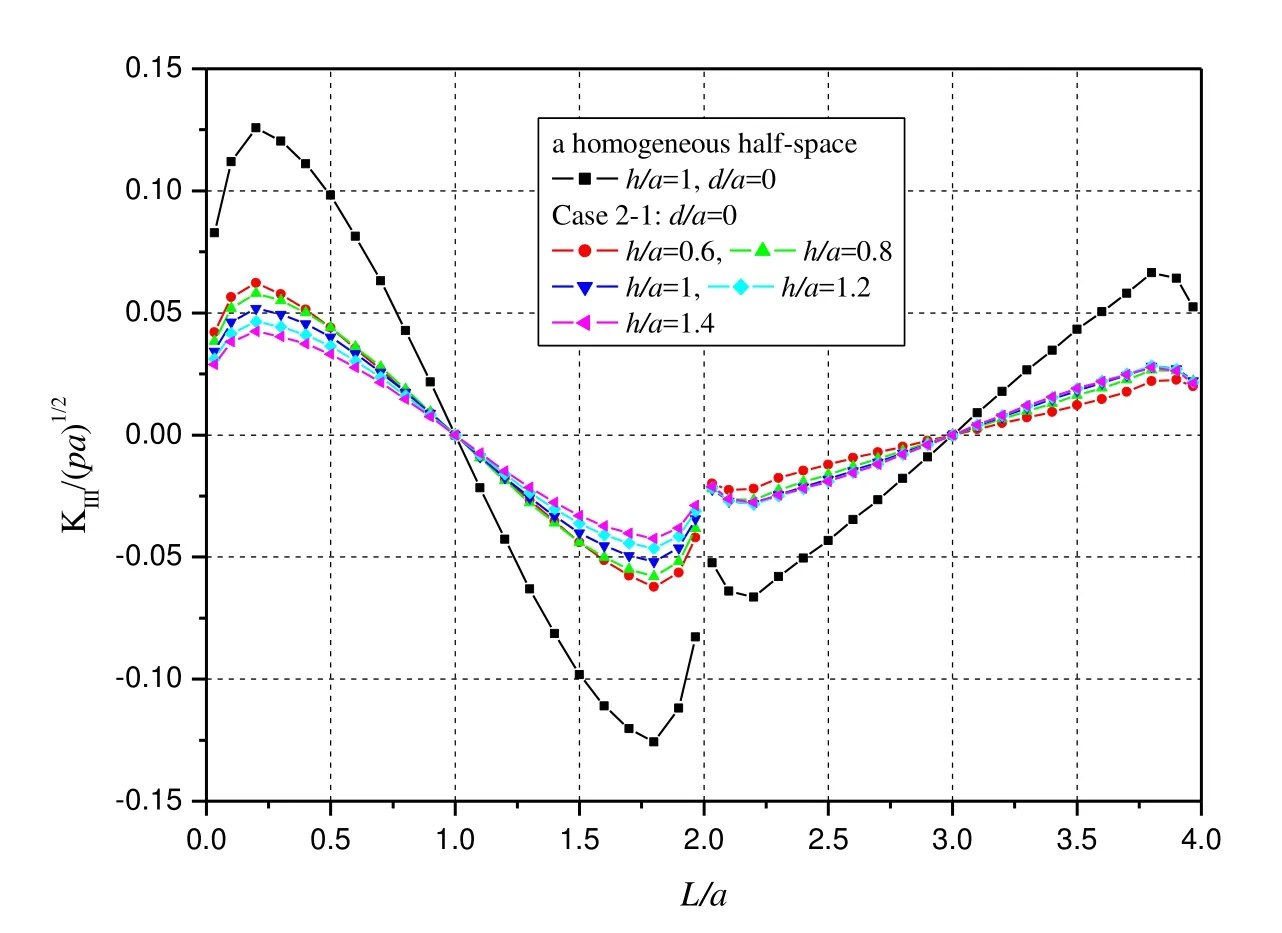
Figure 18:Variations of KIIIwith h for Case 2-1(d=0).

Figure 19:Variations of Sminwith h for Case 2-1(d=0).

It is obvious that the homogeneous medium(Material 3)exert a stronger inf l uence on the sliding discontinuous displacements than the finite layer(Material 1).

6.2.2 Analysis of crack growth

Fig.19 shows the variations of Sminalong the crack front AB and BC using Eq.(4)and the SIF values presented in Figs.17 and 18.From this figure,we can have the following observations:

·Along the crack front AB,the Sminvalues are symmetrical with respect to L/a=1 and the maximum values of Sminappear at L/a=0.2,1.8 for all h/a values.Along the crack front BC,the Sminvalues are symmetrical with respect to L/a=3 and the maximum values of Sminappear at L/a=3 for all h/a values.

·The Sminvalues of the crack for Case 2-1 become much smaller than the ones of the crack in a homogeneous half-space.This means that the crack growth for Case 2-1 becomes more difficult than the ones in a homogeneous halfspace.For Case 2-1,the Sminvalues become small with the depth increasing.Along the crack front BC,the variations of Sminwith the depth h are more obvious than along the crack front AB.

6.3 Case 2-2:E1=E3=E2/2

6.3.1 SIF values of the crack

Figs.20 and 21 illustrate the variations of KIIand KIIIfor Case 2-2.From these fi gures,it can be found that the absolute values of KIIand KIIIfor a homogeneous medium are much smaller than the ones for a layered half-space.This is because the elastic moduli of Materials 1 and 3 have smaller values than Material 2 and the different materials induce larger sliding discontinuous displacements.Along 0＜L/a＜2,the absolute values of KIIincrease for 0.6≤h/a≤1 and decrease for 1≤h/a≤1.4 as the depth h increases.Along 2＜L/a＜4,the absolute values of KIIdecrease as the depth h increases.As the depth h increases,the absolute values of KIIIdecrease in the neighborhood of L/a=0.25 and L/a=1.75 whilst the absolute values of KIIIslightly increase for 0.6≤h/a≤1 and decrease for 1≤h/a≤1.4 along 2＜L/a＜4.Similarly,the homogeneous medium(Material

3)exert a stronger in fl uence on the sliding discontinuous displacements than the fi nite layer(Material 1).

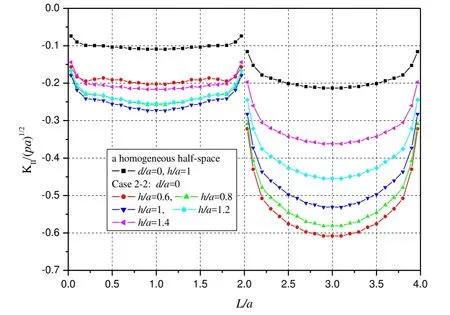
Figure 20:Variations of KIIwith h for Case 2-2(d=0).

Figure 21:Variations of KIIIwith h for Case 2-2(d=0).

Figure 22:Variations of Sminwith h for Case 2-2(d=0).

6.3.2 Analysis of crack growth

Fig.22 shows the variations of Sminalong the crack front AB and BC using Eq.(4)and the SIF values presented in Figs.20 and 21.From this figure,we can have the following observations:

·Along the crack front AB,the Sminvalues are symmetrical with respect to L/a=1 and the maximum values of Sminappear at L/a=0.2,1.8 for all h/a values.Along the crack front BC,the Sminvalues are symmetrical with respect to L/a=3 and the maximum values of Sminappear at L/a=3 for all h/a values.

·The Sminvalues of the crack for Case 2-2 become much larger than the ones of the crack in a homogeneous halfspace.This means that the crack growth for Case 2-1 becomes easier than the ones in a homogeneous half-space.For Case 2-2,the Sminvalues become small with the depth increasing.Along the crack front BC,the variations of Sminwith the depth h are more obvious than along the crack front AB.

7 Conclusions

This paper develops novel methods for the analysis of square-shaped crack problems in a layered half-space subject to the uniform rectangular loadings on the boundary surface.The two numerical methods use the fundamental solution of a layered medium and also utilize the superposition principle in fracture mechanics.

The numerical results show that the fracture modes of the crack under the action of this loading are coupled and the material in the neighborhood of a square-shaped crack exerts an obvious inf l uence on the SIF values of the crack.They also illustrate that the distribution of the SIF values is much related to the horizontal and vertical distances between the crack and the loading.Using the SIF values and the S-criterion on the basis of the strain energy density concept,the minimum values of strain energy density factor at the crack front are calculated and the position and direction of potential crack growth is discussed.It can be found that the strain energy density factor values are obviously affected by the positions of the crack and the materials in the neighborhood of the crack

Acknowledgements

The authors would like to thank the financial supports from the National Natural Science Foundation of China(No.41172242),SDUST Research Fund(2015TDJH104)and the Research Grants Council of Hong Kong SAR Government

Arin,K.；Erdogan F.(1971):Penny-shaped crack in an elastic layer bonded to dissimilar half spaces International Journal of Engineering Science vol.9 no.2,pp.213-232

AlaimoA；Milazzo,A.；Orlando,C.(2013):Applicationofthe3-Dboundaryelement method to delaminated composite structures Engineering Fracture Mechanics vol.110 pp.201-217.

Bai T；Pollard,D.D.(1999):Spacing of fractures in a multiplayer at fracture saturation International Journal of Fracture vol.100 no.4,pp.L23-28

Bains,R.(1992):Boundary element analysis of 3D crack problems:weight function techniques.PhD thesis,Wessex Institute of Technology,UK.

Bains,R.；Aliabadi,M.H.；Rooke,D.P.(1992):Fracture mechanics weight functions in three dimensions:subtraction of fundamental fields.International Journal of Numerical Methods in Engineering,vol.35,no.1,pp.179-202.

Chao,C.K.；Wikarta,A.(2012):Mode-III stress intensity factors of a threephase composite with an eccentric circular inclusion.CMES:Computer Modelling in Engineering&Sciences vol.84,no.5,pp.439-458

Dhaliwal R S.(1973):A two dimensional crack problem for an elastic layer bonded to an infinite elastic medium Journal of Elasticity vol.3,no.2,pp.117-123

Dong,L.T.；Atluri,SN.(2012):SGBEM(usingnon-hyper-singulartractionBIE),and super elements,for non-collinear fatigue-growth analyses of cracks in stiffened panels with composite-patch repairs CMES:Computer Modelling in Engineering&Sciences vol.89,no.5 pp.417-458

Dong,L T.；Atluri,S N.(2013a):Fracture&fatigue analyses:SGBEM-FEM or XFEM?Part 1:2D Structures CMES:Computer Modelling in Engineering&Sciences vol.90,no.2,pp.91146.

Dong,L.；Atluri,S.N.(2013b):Fracture&fatigue analyses:SGBEM-FEM or XFEM?Part 2:3D solids.CMES:Computer Modeling in Engineering&Sciences,vol.90,no.5,pp.379-413.

Dong,L.；Atluri,S.N.(2013c):SGBEM voronoi cells(SVCs),with embedded arbitrary-shaped inclusions,voids,and/or cracks,for micromechanical modeling of heterogeneous materials.CMC:Computers,Materials&Continua vol.33 no.2 pp.111-154.

Hartranft,R.J.；Sih,G.C.(1997):Stress singularity for a crack with arbitrary curved front.Engineering Fracture Mechanics,vol.9,pp.705-718.

Maloney,J.M.；Walton,E.B.；Bruce,C.M.；Van Vliet,K.J.(2008):Inf l uence of finite thickness and stiffness on cellular adhesion-induced deformation of compliant substrata.Physical Review E,vol.78,no.4,pp.1-15.

Murakami,Y.(Ed.)(1987):Stress Intensity Factors Handbook.Oxford:Pergamon Press.

Kuo C H.；Keer L M.(1995):Three-dimensional analysis of cracking in a multilayered composite ASME,Journal of Applied Mechanics vol 62,pp.273-81.

Selvadurai,A.P.S.(1998):The modeling of axisymmetric basal crack evolution in a borehole indentation problem.Engineering Analysis with Boundary Elements,vol.21,no.4,pp.377-383.

Selvadurai,A.P.S.(2000):Fracture evolution during indentation of a brittle elastic solid.Mechanics of Cohesive-Frictional Materials,vol.5,no.4,pp.325-339.Wang,B.L.；Sun,Y.G.；Zhu,Y.(2011):Fracture of a finite piezoelectric layer with a penny-shaped crack.International Journal of Fracture,vol.172,no.1,pp.19-39.

Weaver,J.(1977):Three-dimensional crack analysis.International Journal of Solids and Structures,vol.13,no.4,pp.321-330.

Sih,G.C.(1973):A special theory of crack propagation:methods of analysis and solutions of crack problems,in:G.C.Sih(Ed.),Mechanics of Fracture I,Noordhoof,Leyden.

Sih,G.C.；Cha,C.K.(1974):A fracture criterion for three-dimensional crack problems.Engineering Fracture Mechanics,vol.6,no.4,pp.699-723.

Pan,E.；Yuan,F.G.(2000):Boundary element analysis of three-dimensional crack in anisotropic solids.International Journal of Numerical Methods in Engineering,vol.48,no.2,pp.211-237.

Xiao,H.T.；Yue Z.Q.(2009):A generalized Kelvin solution based BEM for contact problems of elastic indetor on FGMs.CMES:Computer Modelling in Engineering&Sciences,vol.52,no.2,pp.159-179.

Xiao,H.T.；Yue,Z.Q.(2011):A three-dimensional displacement discontinuity method for crack problems in layered rocks.International Journal of Rock Mechanics and Mining Sciences,vol.48,no.3,pp.412-420.

Xiao H T.；Yue Z Q.(2014):Fracture mechanics in layered and graded materials:analysis using boundary element methods Berlin:De Gruyter and Beijing:Higher Education Press

Xiao,H.T.；Yue Z.Q.；Zhao X.M.(2012):A generalized Kelvin solution based method for analyzing elastic fields in heterogeneous rocks due to reservior water impoundment Computers and Geosciences,vol.43 pp.126-136

Yue,Z.Q.(1995):On generalized Kelvin solutions in a multilayered elastic medium.Journal of Elasticity vol.43,no.1,pp.1-43.

Yue,Z.Q.；Xiao,H.T.；Pan,E.(2007):Stress intensity factors of square crack inclined to interface of transversely isotropic bi-material.Engineering Analysis with Boundary Elements,vol.31,no.1,pp.50-56.

Zhang,X.；Jeffrey,R.G.(2006):Numerical studies on crack problems in threelayered elastic media using an image method International Journal of Fracture,vol.139 no.3-4,pp.477-493

1College of Civil Engineering&Architecture,Shandong Univ.of Sci.&Tech.,266590,Qingdao,China.

2Shandong Key Lab of Civil Engineering Disaster Prevention&Mitigation,266590,Qingdao,China.

3Corresponding Author.Tel:+86-532-80681200.E-mail:xiaohongtian@tsinghua.org.cn

4Department of Civil Engineering,The University of Hong Kong,Hong Kong.