中国湿地松立木生物量方程的研建
曾伟生,姚顺彬,肖前辉
(1.国家林业局调查规划设计院,北京 100714;2.国家林业局 华东林业调查规划设计院,浙江 杭州 310019;3.国家林业局 中南林业调查规划设计院,湖南 长沙 410014)
中国湿地松立木生物量方程的研建
曾伟生1,姚顺彬2,肖前辉3
(1.国家林业局调查规划设计院,北京 100714;2.国家林业局 华东林业调查规划设计院,浙江 杭州 310019;3.国家林业局 中南林业调查规划设计院,湖南 长沙 410014)
以我国湿地松154株样木的生物量实测数据为基础,综合利用分段建模方法和非线性误差变量联立方程组方法,建立了与立木材积方程相容的地上生物量方程和生物量转换因子模型,以及与地上生物量方程相容的地下生物量方程和根茎比模型。结果表明:所建地上生物量方程的平均预估误差小于5%,地下生物量方程的平均预估误差小于10%,全树生物量估计的平均预估误差小于3%,完全可满足森林生物量计量的精度要求,从而为我国湿地松林的生物量估计及碳汇能力评估提供了计量依据。
中国湿地松;地上生物量;地下生物量;生物量转换因子;根茎比
湿地松Pinus elliottii原产于美国东南部。由于具有早期生长快、木材质量好、松脂产量高、适应性强等优良特性,从20世纪30年代开始,在我国亚热带地区广泛引种。目前已成为我国南方丘陵区主要造林树种之一。根据第七次全国森林资源清查结果,我国湿地松林面积达到120万hm2以上,蓄积达0.5亿m3左右,大约相当于人工马尾松林的1/3。国内最早关于湿地松生物量的研究可以追溯到上世纪90年代初[1],此后陆续有学者研究过湿地松的生物量,但为数不多且仅限于福建、江西、湖南等省的局部地区[2-7]。近年来,随着林业在应对气候变化中特殊地位的日益凸显,森林生物量研究已成为国内外林业的热点问题之一,并已取得大量研究成果[8-21]。本文以我国湿地松为对象,综合利用分段建模方法和非线性误差变量联立方程组方法,研究建立了与立木材积相容的地上生物量方程、生物量转换因子模型及根茎比模型,为湿地松林的生物量估计提供了可靠依据,对森林碳储量监测和碳汇能力评估具有重要意义。
1 数 据
根据第七次全国森林资源清查结果,我国湿地松分布于浙江、福建、江西、河南、湖北、湖南、广东、广西、重庆、四川、贵州等11省(市、区),其中福建、江西、湖南、广东、广西5省区的湿地松蓄积占到了全部蓄积的93.75%。因此,本研究的湿地松立木生物量建模样本采集自上述5省区,共计154株样木,其中福建10株,江西50株,湖南20株,广东44株,广西30株,样木数量与各省湿地松资源数大体呈正比。全部样木数按 2、4、6、8、12、16、20、24、28cm和32cm以上10个径阶均匀配置,每个径阶约15株,且尽可能按不同树高级(分3~5个树高级)均匀配置。野外实测样木胸径、树高及树干、树枝、树叶鲜重,并分别选择样品(其中树干分干材和干皮)带回实验室测定含水率,推算各部分干重,从而得到地上生物量及树干、树冠、干材、干皮、树枝、树叶等各个分量。其中有约1/3样木(50株)同时测定了地下生物量。表1为湿地松建模样本的基本情况。
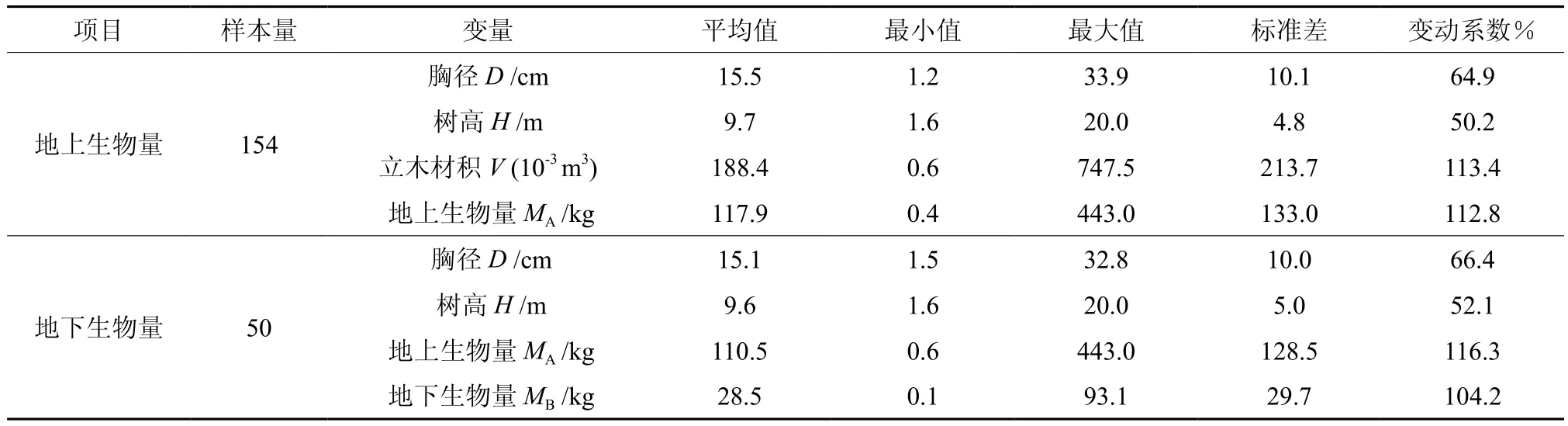
表1 湿地松立木生物量建模样本基本情况Table 1 General situations of biomass modeling sample of slash pine
2 方 法
立木生物量方程的常用结构形式为[13-15]:

式中:y为地上生物量MA或地下生物量MB;xj为胸径D、树高H等反映林木大小的变量;βj为参数;ε为误差项。由于立木生物量数据具有明显的异方差,参数估计时应采取消除异方差的措施。本文采用加权回归方法,并利用普通回归估计的残差推导的特定权函数进行加权回归[22]。由于基于胸径的一元模型和基于胸径与树高的二元模型应用最为广泛,本文将同时建立一元和二元立木生物量方程。
2.1 地上生物量建模
立木地上生物量通过生物量转换因子与立木材积相关联。由于生物量转换因子也是生物量评估中的重要参数,因此一般同时建立与立木材积相容的地上生物量方程及生物量转换因子模型[13-14]。另外,一元模型和二元模型之间,也可通过胸径—树高回归模型相互关联。因此,完全可以通过引入立木材积方程和胸径—树高回归模型,将一元和二元地上生物量方程及生物量转换因子模型关联起来,采用误差变量联立方程组方法构建一体化模型系统[23-24]。这样既充分利用了样本信息,又保证了生物量方程和材积方程之间、一元模型和二元模型之间的相容性。一体化误差变量联立方程组形如下式:
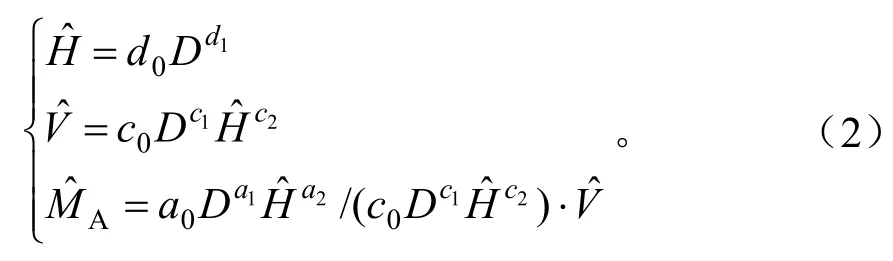
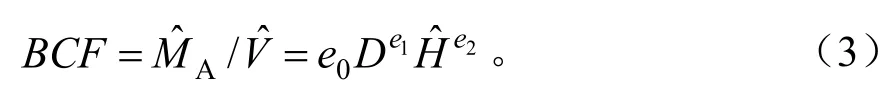
它们之间的参数存在以下关系:
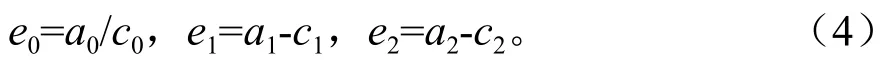
联立方程组(2)的求解可采用ForStat软件[23]。求得模型的参数估计值后,再分别计算地上生物量和立木材积方程的以下6项统计指标[25]:确定系数(R2)、估计值的标准误(SEE)、平均预估误差(MPE)、总相对误差(TRE)、平均系统误差(MSE)和平均百分标准误差(MPSE),其中TRE和MSE两项指标还分径阶进行评定,如果存在明显的系统偏差,还有必要考虑分段建模[14]。
2.2 地下生物量建模
立木地下生物量通过根茎比与地上生物量相关联。由于根茎比也是生物量评估中的重要参数,因此一般同时建立与地上生物量相容的地下生物量方程及根茎比模型[12]。同样,一元模型和二元模型之间,也可通过胸径—树高回归模型相互关联。地下生物量的一体化误差变量联立方程组形如下式:分别为树高、地上生物量和地下生物量的估计值,属于误差变量;D为胸径,视为无误差变量;ai、bi、di为参数,其中树高模型参数d0、d1采用方程组(2)的结果。方程组(5)除包含地上和地下生物量方程以外,还包含了根茎比(RSR)模型:
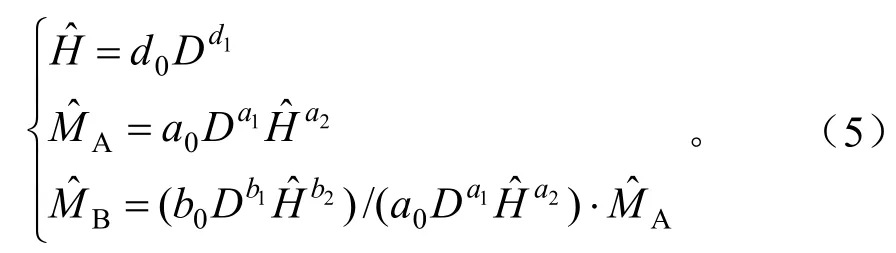
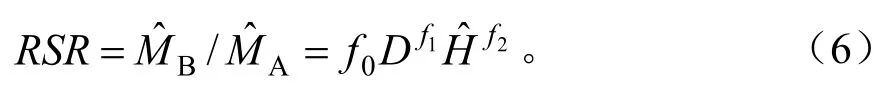
它们之间的参数存在以下关系:
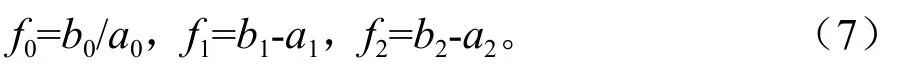
同样,将方程组(5)中第1行的式子代入第2、3行的式子及式(6),即得到相应的一元模型。联立方程组(5)的求解同样采用ForStat软件。求得模型的参数估计值后,再计算地下生物量的相关统计指标。如果统计指标分径阶检验存在明显的系统偏差,也需考虑分段建模。
3 结 果
3.1 地上生物量方程
利用湿地松的154株样木的地上生物量、立木材积、胸径、树高成套数据,采用ForStat软件中的“非线性误差变量联立方程组”方法[23],拟合联立方程组(2),其结果如下:
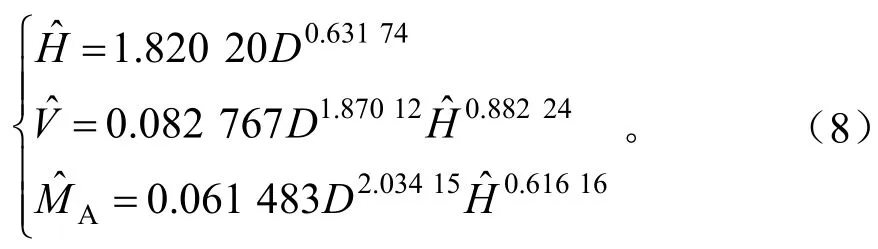
方程组(8)中第2、3行中的 Hˆ用第1行的结果代入就得到了相容性一元立木材积方程和地上生物量方程;如果改用实测值,就是二元方程。以此为基础可以计算一元和二元立木材积方程及地上生物量方程的各项统计指标,其中地上生物量方程的统计指标见表2。

表2 湿地松地上生物量模型的统计指标Table 2 Statistics of aboveground biomass equations of slash pine
从前面的4项指标看,总体效果尚可,尤其是核心指标平均预估误差小于5%,达到了预期的精度要求;总相对误差TRE也都接近于0。但是,后面的2项指标明显偏大,尤其是平均系统误差MSE显著偏离理想值0。如果再分径阶检验TRE和MSE,则发现各径阶的估计值误差偏大,尤其是最小径阶的TRE和MSE甚至均超过了100%。因此,进一步采用分段建模方法[14],分别对5cm以上及5cm以下建立模型,其参数估计结果见表3,地上生物量分段模型的统计指标见表4。
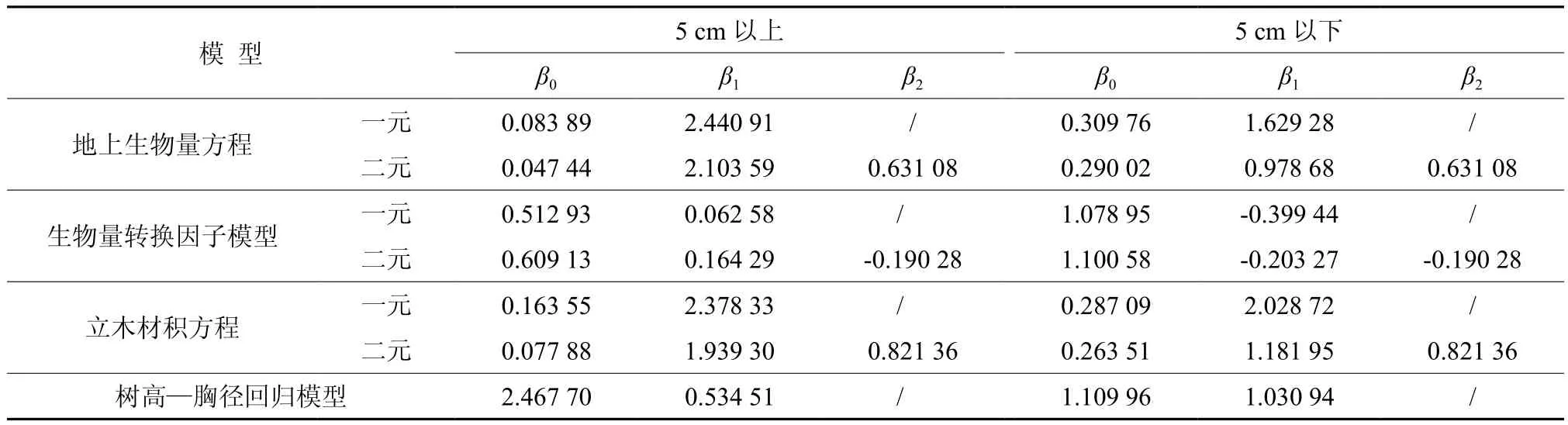
表3 湿地松地上生物量联立方程组分段建模的参数估计结果Table 3 Parameter estimation of simultaneous aboveground biomass equations of slash pine based on segmented modeling
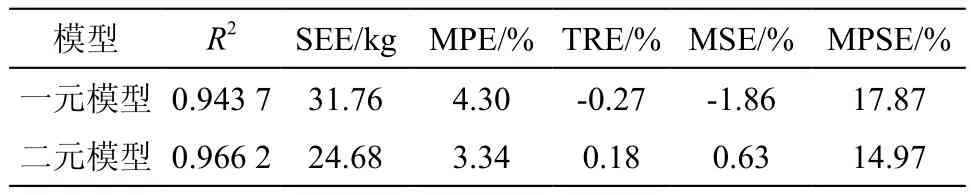
表4 湿地松地上生物量分段模型的统计指标Table 4 Statistics of aboveground biomass equations of slash pine based on segmented modeling
表4中的统计指标与表2相比,R2、SEE、MPE、TRE这4项指标差异不大,但后面的2项指标则有明显改进,平均系统误差MSE已经接近于0,平均百分标准误差MPSE比前述常规建模结果降低了10个以上百分点,其中二元模型的MPSE只有前述结果的一半。这是因为,分段建模方法有效消除了原来径阶之间存在的系统误差,尤其是消除了最小径阶的极端正偏差。以二元模型为例,表5列出了TRE和MSE 2项指标分径阶检验结果的对比,明显可以看出,分段模型10个径阶的TRE和MSE均在±10%以内,且有7个径阶均在±5%以内;而常规模型2cm径阶的MSE达到179.23%,TRE也达到140.47%,8cm径阶的TRE和MSE均小于-17%,相邻的6、12cm径阶也存在明显的负偏差。图1给出了这2种二元地上生物量模型的相对残差分布对比,分段模型基本呈比较理想的随机分布。综合来看,表3中的分段建模结果要明显优于常规建模结果。
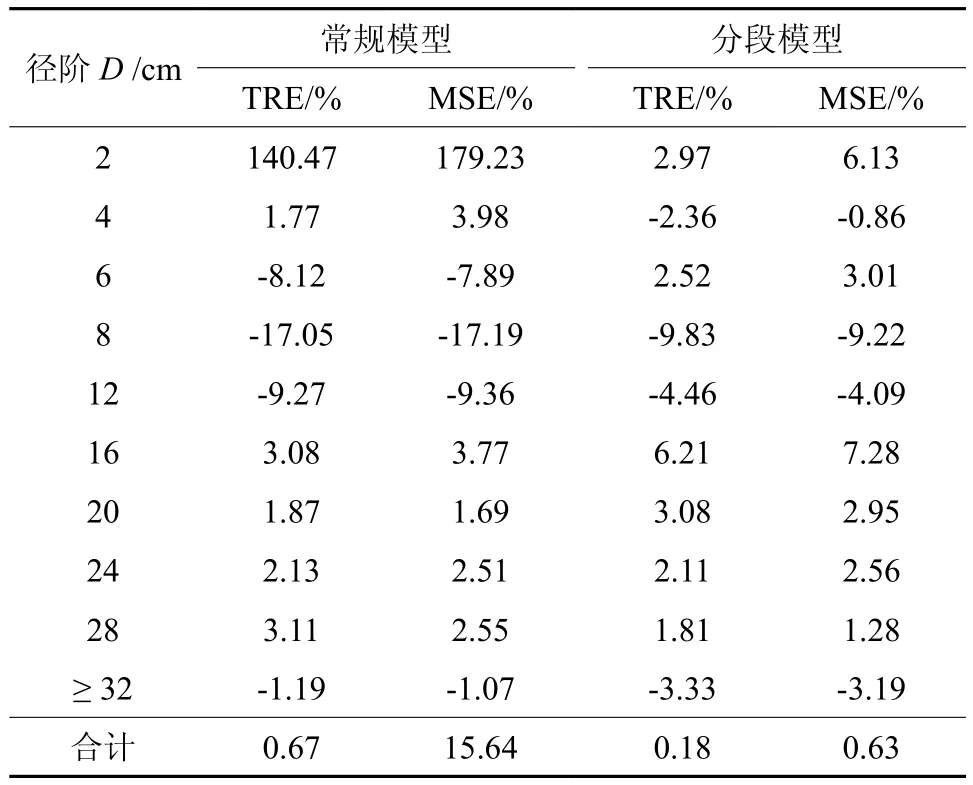
表5 湿地松2种地上生物量模型分径阶检验结果对比Table 5 Comparison of test results of two aboveground biomass equations of slash pine by diameter-class
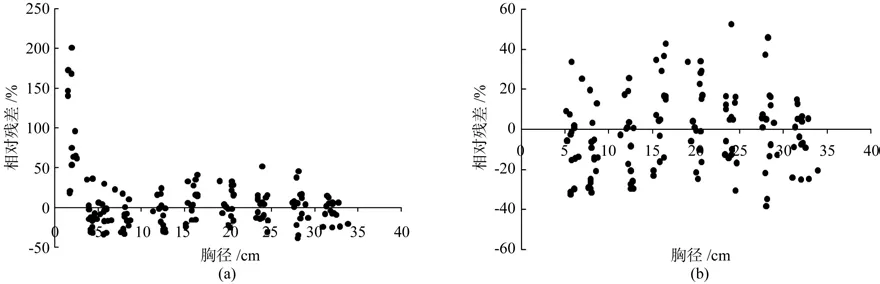
图1 湿地松2种地上生物量模型的相对残差分布对比Fig.1 Comparison of relative residual errors between two aboveground biomass equations of slash pine
3.2 地下生物量方程
利用湿地松的50株样木的地上生物量、地下生物量、胸径、树高成套数据,采用ForStat软件中的“非线性误差变量联立方程组”方法[23],拟合联立方程组(5)。根据对拟合结果的分析,发现与地上生物量模型类似,各径阶估计值的误差明显偏大,存在一定的系统偏差。为此,同样采用分段建模方法[14],分别对5cm以上及5cm以下建立模型,其参数估计结果见表6,地下生物量分段模型的统计指标见表7。
在实际应用时,采用表3中的地上生物量方程及表6中的根茎比模型,分别计算湿地松地上和地下生物量及总生物量。其中,地下生物量方程可由表3中的地上生物量方程与表6中的根茎比模型相乘得到。
一元地下生物量方程:
MB=0.043 570D2.22877(D≥5cm);
MB=0.071 442D1.92151(D<5cm)。
二元地下生物量方程:
MB=0.035 263D2.10359H0.23419(D≥5cm);
MB=0.071 994D1.66011H0.23419(D<5cm)。
由于地下生物量与地上生物量相关紧密,可以把建立表3中地上生物量模型的154株样木视为一重样本,把建立表6中地下生物量模型的50株样木视为二重样本,按(9)式计算最后综合的地下生物量模型的平均预估误差:

表6 湿地松地下生物量联立方程组分段建模的参数估计结果†Table 6 Parameter estimation of simultaneous belowground biomass equations of slash pine based on segmented modeling
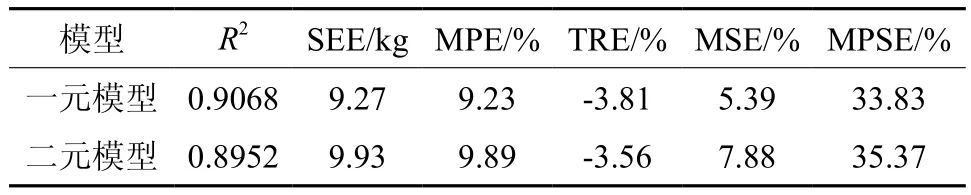
表7 湿地松地下生物量分段模型的统计指标Table 7 Statistics of belowground biomass equations of slash pine based on segmented modeling
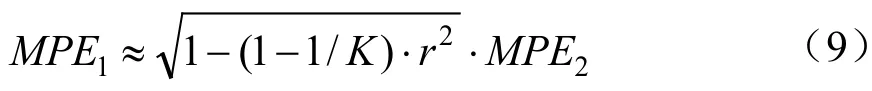
式中:K为一重样本与二重样本单元数之比,此处为3.08;r为二重样本地下生物量与地上生物量之间的相关系数,经计算r=0.938 9;MPE2为利用二重样本建立的地下生物量模型估计值的平均预估误差,对一元和二元模型为9.23%和9.89%;MPE1为综合一重样本后得到的地下生物量模型估计值的平均预估误差,对一元和二元模型经计算分别为5.87%和6.29%。
立木总生物量的平均预估误差可根据地上生物量和地下生物量的误差,按和的误差传播公式计算。如对于一元模型,按地上生物量平均预估误差4.30%、地下生物量平均预估误差5.87%,用和的误差传播公式进行计算,林木总生物量的平均预估误差约为2.50%。
4 结 论
本文以我国湿地松为研究对象,以154株样木的地上生物量实测数据和50株样木的地下生物量实测数据为基础,综合利用分段建模方法和非线性误差变量联立方程组方法,建立了与立木材积相容的地上生物量方程和生物量转换因子模型,以及与地上生物量相容的地下生物量方程和根茎比模型,为湿地松林的生物量估计及碳汇能力评估提供了计量依据。根据建模结果,可以得出以下结论。
1)利用单一参数的生物量模型难以保证5cm以上和5cm以下全部林木的估计效果,采用分段建模方法可有效解决小径阶的偏估问题,确保各个径阶的生物量估计无明显系统误差。
2)利用非线性误差变量联立方程组方法,可构建集一元模型和二元模型为一体、使生物量方程与立木材积方程相协调的相容性模型系统,确保了各个模型之间的内在联系及生物量估计值与材积估计值的协调统一。
3)本研究建立的湿地松地上生物量方程,其平均预估误差在5%以内,地下生物量方程的平均预估误差在10%以内,全树总生物量的平均预估误差基本可控制内3%以内。所建地上生物量方程、地下生物量方程、生物量转换因子模型及根茎比模型完全可应用于我国湿地松林的生物量估计。
[1] 汪企明,石有光.江苏省湿地松人工林生物量的初步研究[J].植物生态学与地植物学学报,1990,14(1):1-12.
[2] 张连水,庄志贤,李秀全.湿地松地上生物量变化研究[J].林业科技开发,2001,15(增刊):42-43.
[3] 赖建强.闽南湿地松生物量估算模型研究[J].林业勘察设计,2005,(2):98-101.
[4] 李轩然,刘琪璟,陈永瑞,等.千烟洲人工林主要树种地上生物量的估算[J].应用生态学报,2006,17(8):1382-1388.
[5] 陈振勤.连江沿海山地湿地松人工林生物量测定试验[J].林业勘察设计,2008,(2):16-19.
[6] 张维轴.屏南县湿地松人工林生物量及生产力的研究[J].林业勘察设计,2010,(2):11-16.
[7] 肖兴翠,李志辉,唐作钧,等.林分密度对湿地松生物量及生产力的影响[J].中南林业科技大学学报,2011,31(3):123-129.
[8] 罗云建,张小全,侯振宏,等.我国落叶松林生物量碳计量参数的初步研究[J].植物生态学报,2007,31(6):1111-1118.
[9] 程堂仁,冯 菁,马钦彦,等.小陇山油松林乔木层生物量相容性线性模型[J].生态学杂志,2008,27(3):317-322.
[10] 曾伟生,肖前辉,胡 觉,等.中国南方马尾松立木生物量模型研建[J].中南林业科技大学学报,2010,30(5):50-56.
[11] 尹艳豹,曾伟生,唐守正.中国东北落叶松立木生物量模型研建[J].东北林业大学学报,2010,38(9):23-26.
[12] 曾伟生,唐守正.东北落叶松和南方马尾松地下生物量模型研建[J].北京林业大学学报,2011,33(2):1-6.
[13] 曾伟生,夏忠胜,朱 松,等.贵州人工杉木相容性立木材积和地上生物量方程的建立[J].北京林业大学学报,2011,33(4):1-6.
[14] 党永峰,王雪军,曾伟生.用分段建模方法建立东北落叶松相容性立木材积和地上生物量方程[J].林业科学研究,2012,25(5):558-563.
[15] Zianis D,Muukkonen P,Mäkipää R,et al.Biomass and stem volume equations for tree species in Europe[J].Silva Fennica(Monographs 4),2005.
[16] Snorrason A,Einarsson S F.Single-tree Biomass and Stem Volume Functions for Eleven Tree Species Used in Icelandic Forestry[J].Icelandic.Agric.Sci.,2006,19:15-24.
[17] Muukkonen P.Generalized Allometric Volume and Biomass Equations for Some Tree Species in Europe[J].Eur.J.Forest Res.,2007,126:157-166.
[18] Case B,Hall R J.Assessing Prediction Errors of Generalized Tree Biomass and Volume Equations for the Boreal Forest Region of West-central Canada[J].Can.J.For.Res.,2008,38:878-889.
[19] Návar J.Allometric Equations for Tree Species and Carbon Stocks for Forests of Northwestern Mexico[J].Forest Ecology and Management,2009,257:427-434.
[20] Blujdea V N B,Pilli R,Dutca I,et al.Allometric biomass equations for young broadleaved trees in plantations in Romania[J].Forest Ecology and Management,2012,264:172-184.
[21] Fayolle A,Doucet J-L,Gillet J-F,et al.Tree allometry in Central Africa:Testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks[J].Forest Ecology and Management,2013,305:29-37.
[22] 曾伟生,唐守正.非线性模型对数回归的偏差校正及与加权回归的对比分析[J].林业科学研究,2011,24(2):137-143.
[23] 唐守正,郎奎建,李海奎.统计和生物数学模型计算(ForStat教程)[M].北京:科学出版社,2008.
[24] 曾伟生.利用误差变量联立方程组建立一元立木材积模型和胸径地径回归模型[J].中南林业调查规划,2012,31(4):1-4.
[25] 曾伟生,唐守正.立木生物量模型的优度评价和精度分析[J].林业科学,2011,47(11):106-113.
Construction of individual tree biomass equations for Pinus elliottii in China
ZENG Wei-Sheng1,YAO Shun-Bin2,XIAO Qian-Hui3
(1.Academy of Forest Inventory and Planning,State Forestry Administration,Beijing 100714,China;2.East China Forest Inventory and Planning Institute,State Forestry Administration,Hangzhou 310019,Zhejiang,China;3.Central South Forest Inventory and Planning Institute,State Forestry Administration,Changsha 410014,Hunan,China)
Based on the measured biomass data of 154 sample trees for slash pine(Pinus elliottii)in China,at fi rst the individual tree aboveground biomass equations and biomass conversion factor(BCF)models compatible to tree volume equations were constructed by using the segmented modeling approach and nonlinear error-in-variable simultaneous equations,then the individual tree belowground biomass equations and root-to-shoot ratio(RSR)models compatible to aboveground biomass equations were also established.The mean prediction errors(MPE’s)of developed aboveground biomass equations were less than 5%,the MPE’s of belowground biomass equations were less than 10%,and the MPE’s of whole tree biomass estimates were less than 3%,which can satisfy the precision requirement of biomass estimation.Therefore,the constructed biomass equations in this paper can provide quantitative basis for biomass estimation and carbon assessment of slash pine forests in China.
Pinus elliottii in China; above-ground biomass; below-ground biomass; biomass conversion factor; root-to-shoot ratio
S791.246;S718.55+6
A
1673-923X(2015)01-0008-06
10.14067/j.cnki.1673-923x.2015.01.002
2013-10-10
国家林业局财政预算项目“森林资源清查与动态监测”(2130208)
曾伟生,教授级高工,博士;E-mail:447892345@qq.com
曾伟生,姚顺彬 ,肖前辉.中国湿地松立木生物量方程的研建[J].中南林业科技大学学报,2015,35(1):8-13.
致谢:感谢国家林业局森林资源连续清查森林生物量调查建模项目为本研究提供了湿地松的生物量实测资料,并对国家林业局华东林业调查规划设计院项目组及相关省区林业主管部门为样本资料采集所付出的努力表示感谢!
[本文编校:谢荣秀]

