高光谱多种变换对松林郁闭度的估测效果对比分析

许章华 ，刘 健 ，余坤勇

（1.福州大学 环境与资源学院，福建 福州 350116；2.福建农林大学 a.福建省资源环境监测与可持续经营利用重点实验室；b.林学院，福建 福州 350002；3.三明学院，福建 三明 365000）

高光谱多种变换对松林郁闭度的估测效果对比分析

许章华1，2a，刘 健2a，b，3，余坤勇2a，b，3

（1.福州大学 环境与资源学院，福建 福州 350116；2.福建农林大学 a.福建省资源环境监测与可持续经营利用重点实验室；b.林学院，福建 福州 350002；3.三明学院，福建 三明 365000）

以采集于长汀县、建阳区与延平区的60组松林郁闭度及高光谱数据为建模组，对实测高光谱反射率进行多种变换。基于灰色关联度分析法选择与松林郁闭度关联度最高的两个波长，分别建立以反射率、反射率二次方根、反射率对数、反射率倒数、反射率对数的倒数、反射率一阶微分、反射率二次方根一阶微分、反射率对数一阶微分、反射率倒数一阶微分、反射率对数的倒数一阶微分为自变量的松林郁闭度估测模型，比较模型决定系数R2及均方根误差。以采集于将乐县与华安县的20组样本为验证组，建立各模型郁闭度估测值与实测值间的数学关系，并比较R2、均方根误差及平均估测精度。结果表明，以反射率二次方根一阶微分为自变量对松林郁闭度有较理想的估测效果，平均估测精度达85.57%，其后依次为以反射率对数的倒数一阶微分、反射率、反射率二次方根、反射率对数、反射率倒数、反射率对数一阶微分为自变量的估测模型，而反射率对数的倒数、反射率一阶微分、反射率倒数一阶微分为自变量的模型则不具备对松林郁闭度的估测能力。

松林郁闭度；高光谱数据；高光谱变换；估测模型

郁闭度（Canopy density）是指森林中乔木树冠遮蔽地面的程度，亦即树冠垂直投影面积与林地面积之比，通常以十分位数表示。在森林经营管理过程中，郁闭度是涉及最为频繁的指标之一，它不仅可反映林分的疏密程度，同时亦与植被指数（如NDVI）、叶面积指数（LAI）等密切相关[1-2]，是森林健康的重要响应特征[3]。目前，在林业生产中，郁闭度的测定方法主要有：目测法、树冠投影法、样线法与样点法等[4]。近年来，运用遥感技术进行郁闭度估测的研究成果方兴未艾。例如，Franklin[5]利用机载光谱仪数据、SPOT全色数据及TM影像实现了亚高山森林树种及其郁闭度的判别；Baynes[6]基于Landsat数据与FCD制图法实实现了森林郁闭度的大尺度估测；吴飏等[7]在光谱等传统特征的基础上，结合遥感图像的纹理特征估测森林郁闭度；李宇昊等[8]则利用高分辨率航空数码影像，结合色彩特征实现森林郁闭度的估测。综观已有的郁闭度反演模型不难发现，成像遥感能较敏感地反映森林郁闭度，而深入挖掘非成像光谱数据与郁闭度之间的耦合关系则为前者提供重要基础。本文以松林郁闭度为研究对象，比较实测高光谱数据不同变换形式对郁闭度的估测效果，为有效应用光谱信息，优化森林郁闭度反演提供参考。

1 研究区概况

2012年2～5月于福建省宁德市、福清市、莆田市、南安市、安溪县、云霄县、华安县、长汀县、三明市、沙县、将乐县、南平市（现南平市延平区）、建阳市（现南平市建阳区）13个县（市、区）开展松林调查。本文选择长汀县（25°19′～ 26°02′N，116°01′～ 116°39′E）、建阳区（27°06′～ 27°43′N，117°31′～ 118°38′E）、将乐县（26°26′～ 27°04′N，117°05′～ 117°40′E）、延平区（26°15′～ 28°19′ N，117°00′～ 119°17′ E）、华安县（24°38′～ 25°12′N， 117°16′～ 117°42′E）作为研究区。各县（区）在自然禀赋上相似度较高，生态环境较好，森林覆盖率均在75%左右，将乐县更是接近85%，居全省之首。各县（区）人工林、用材林比重大，马尾松等松属植物资源丰富，成为区域用材的重要支柱及森林可持续发展的重要支撑。

2 研究方法

2.1 松林郁闭度与光谱测定

于松林小班内以30 m×30 m为单元，获取松林郁闭度及高光谱数据。在单元内采用抬头望目测法记录郁闭度值；选择可代表该单元林分特征的位置，测定松林冠层光谱，利用手持GPS获取坐标信息，并用红漆在周围树干上做记号。松林冠层光谱测定采用合肥仪思特光电技术有限公司生产的ISI921VF-256野外地物光谱辐射计，波长范围为可见-近红外的380～1 050 nm，波段数为256，光谱分辨率为4 nm，视场角3°；天气要求为晴朗少云，测量平均精度N设为3，每转换1个位置均对照白板予以校正。光谱测定过程中，需要借助地形差及竹竿测得松林冠层光谱，部分条件不足区域通过采集离体样本现场测量，由此测得松林冠层光谱数据。本文采用其中的80组数据，将其分为建模组与验证组。建模组样本来自于长汀县、建阳区与延平区，共60组；验证组数据采集自将乐县与华安县，共20组。测点分布见图1。

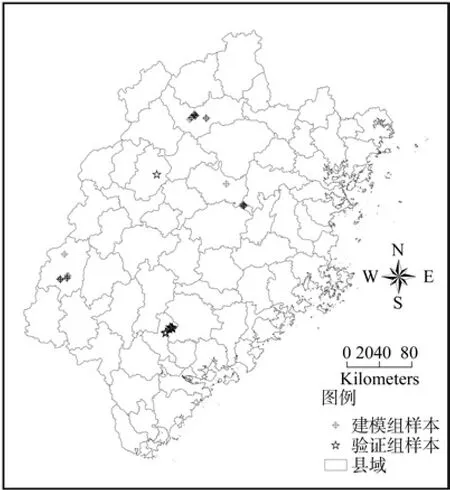
图1 松林郁闭度与高光谱测点分布Fig.1 Pine forests canopy density and hyper-spectrum points distribution

2.2 实测高光谱变换方法

实测高光谱数据中可挖掘的信息十分丰富，对光谱数据进行数学变换是数据挖掘的重要途径之一。参考前人研究方法[9]，对光谱反射率数据进行二次方根、对数、倒数、对数的倒数、一阶微分、二次方根一阶微分、对数一阶微分、倒数一阶微分、对数的倒数一阶微分等多种变换。

2.3 灰色关联度分析

灰色系统理论是我国学者邓聚龙教授于20世纪80年代前期提出的用于控制和预测的新理论、新技术，目前已广泛应用于各个学科领域。关联度是对两个系统或两个因素之间关联性大小的度量，它描述系统发展过程中因素间相对变化的情况，若两者在发展过程中的相对变化基本一致，则认为两者的关联度大，反之则关联度小。灰色关联度分析法是建立在灰色理论基础上的一种对系统发展变化态势的定量描述。它根据评价因素间发展态势的相似和相异程度来确定评价因素的关联程度；其核心内容是计算关联系数与关联度。

本文采用灰色关联度分析法对松林冠层高光谱-松林郁闭度的关联度进行定量描述，以获取二者的相关性。

2.4 估测模型构建与检验方法

逐波段筛选380～1 050 nm范围内相关系数最高的波段位置2个，以其作为松林郁闭度估测模型的自变量。数学模型建立的方法众多，如逐步回归、最小二乘回归、主分量回归、偏最小二乘回归等[10-11]。本文仅采用多元线性回归法建立松林郁闭度的估测模型，重点在于比较实测高光谱不同变换方式对松林郁闭度的估测效果。

估测模型检验分为两大步骤：

（1）计算各模型的决定系数R2及均方根误差E，其计算公式为：

（2）将验证组样本代入各模型，计算平均估测精度f，其计算公式为：

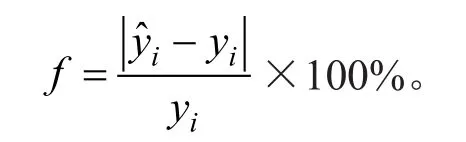
上述各式中， xi、yi分别是第i个样本的自变量值与因变量值；分别为自变量与因变量的平均值；为因变量的估测值；n为样本数。同时拟合验证组数据及各模型估测值的数学关系，计算其决定系数R2及均方根误差。

经上述指标，综合比较实测高光谱各变换形式对松林郁闭度的估测效果。

3 结果与分析

3.1 高光谱不同变换形式与松林郁闭度的关联度排序

分别计算不同变换形式下各波长值与松林郁闭度的关联度，并予以排序，选择关联度排名最高的两个波长（见表1）。表1显示，各种变换形式下，关联度最高的两个波长其关联度均超过0.75，经一阶微分变换后，关联度接近于1。

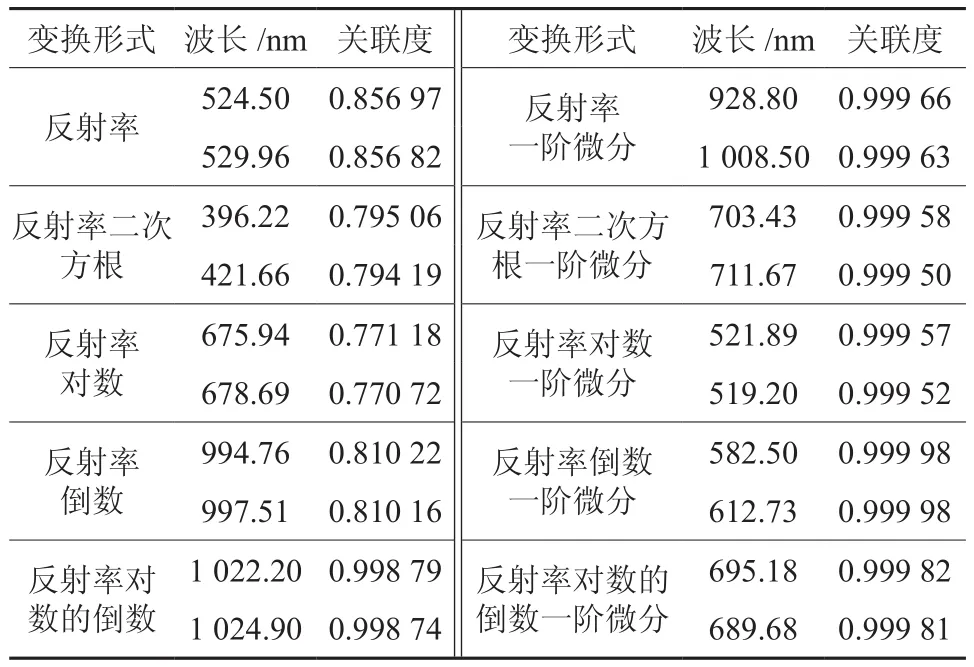
表1 高光谱不同变换形式与松林郁闭度的关联度（关联系数ζ=0.5）Table 1 Correlations among hyper-spectral different transformation methods and pine forests canopy density (correlation coefficient ζ = 0.5)

3.2 松林郁闭度估测模型的建立

以建模组关联度排序前两名的波长为自变量，分别建立高光谱不同变换形式下的松林郁闭度多元线性模型，并对各模型分别计算其R2、E和P值，结果见表2。

由表2可看出，以反射率对数的倒数、反射率一阶微分、反射率倒数一阶微分为自变量的郁闭度估测模型的决定系数R2分别为0.073 3、0.004 6、0.008 3，均未通过P＜0.05的显著性检验，无法实现松林郁闭度的有效估测。余下的7个模型均通过P＜0.05的显著性检验，决定系数R2排序为：反射率二次方根一阶微分＞反射率＞反射率对数的倒数一阶微分＞反射率二次方根＞反射率对数＞反射率倒数＞反射率对数一阶微分，其中，以反射率二次方根一阶微分、反射率、反射率对数的倒数一阶微分为自变量的估测模型的R2超过0.5。均方根误差与决定系数R2正好呈负相关关系，R2越大，E越小。

3.3 松林郁闭度估测精度验证

进一步将验证组中的20组样本分别代入各模型，计算各模型下的松林郁闭度估测值，建立各估测值与实测值的关系模型，并计算平均估测精度（见图2）。

从决定系数R2来看，反射率二次方根一阶微分＞反射率对数的倒数一阶微分＞反射率二次方根＞反射率＞反射率对数＞反射率倒数＞反射率对数一阶微分。从均方根误差来看，反射率二次方根＜反射率对数的倒数一阶微分＜反射率对数一阶微分＜反射率二次方根一阶微分＜反射率对数＜反射率＜反射率倒数。以反射率、反射率二次方根、反射率对数、反射率倒数、反射率二次方根一阶微分、反射率对数一阶微分、反射率对数的倒数一阶微分为自变量的松林郁闭度模型的平均估测精度依次为：79.10%、75.28%、74.51%、68.31%、85.57%、67.40%、76.91%， 反射率二次方根一阶微分平均估测精度最高，超过85%；而反射率倒数、反射率对数一阶微分平均估测精度最低，均低于70%；其余4个模型的平均估测精度介于74%～80%之间。

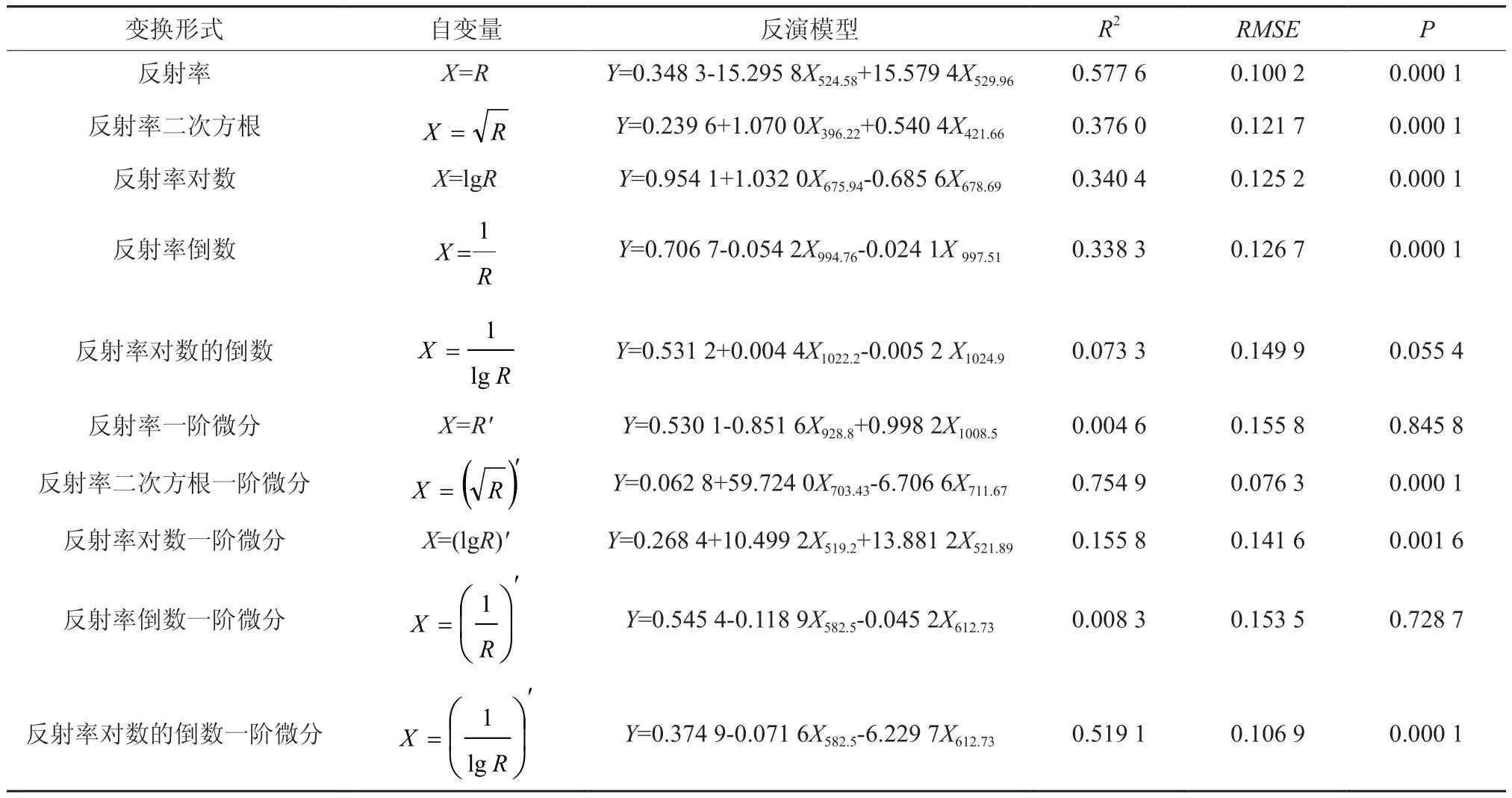
表2 高光谱不同变换形式下的松林郁闭度多元线性模型Table 2 Pine forests canopy density multivariate linear models with hyper-spectral different transformation methods

3.4 结果分析

以上研究结果表明，反射率二次方根一阶微分的估测结果对松林实测郁闭度的解释程度高于反射率对数的倒数一阶微分，高于反射率二次方根，高于反射率，高于反射率对数，高于反射率倒数，高于反射率对数一阶微分，模型的平均估测精度最高，达85.57%，高于反射率的79.10%，高于射率对数的倒数一阶微分的76.91%，高于反射率二次方根的75.28%，高于反射率对数的74.51%，高于反射率倒数的68.31%，高于反射率对数一阶微分的67.40%。

本文综合以上各检验指标，对各模型估测效果进行从优至劣的排序依次为：反射率二次方根一阶微分、反射率对数的倒数一阶微分、反射率、反射率二次方根、反射率对数、反射率倒数、反射率对数一阶微分。

4 结 论

对实测松林高光谱数据进行二次方根、对数、倒数、对数的倒数、一阶微分、二次方根一阶微分、对数一阶微分、倒数一阶微分、对数的倒数一阶微分等多种不同方式的变换，利用灰色关联度分析法选择各变换形式下与松林郁闭度关联度最高的前两个波长，结果显示：524.5、529.96 nm位置上的反射率与松林郁闭度的关联度分别达0.856 97、0.856 82；396.22、421.66 nm位置上的反射率二次方根与郁闭度的关联度分别为0.795 06、0.794 19；675.94、678.69 nm位置上的反射率对数与郁闭度的关联度分别为0.771 18、0.770 72；994.76、997.51 nm位置上的反射率倒数与郁闭度的关联度分别为0.810 22、0.810 16；1 022.2、1 024.9 nm位置上的反射率对数的倒数与郁闭度的关联度分别为0.998 79、0.998 74；上述各形式再经一阶微分变换后，与郁闭度的关联度均得到提升，928.8、1 008.5 nm位置上的反射率一阶微分与松林郁闭度的关联度分别达0.999 66、0.999 63；703.43、711.67 nm位置上的反射率二次方根一阶微分与郁闭度的关联度分别达0.999 58、0.999 50；521.89、519.2 nm位置上的反射率对数一阶微分与郁闭度的关联度分别达0.999 57、0.999 52；582.50、612.73 nm位置上的反射率倒数一阶微分与郁闭度的关联度均达0.999 98；695.18、689.68 nm位置上的反射率对数的倒数一阶微分与郁闭度的关联度分别达0.999 82、0.999 81。

基于关联度最高的前两个波长，分别建立松林郁闭度估测模型，以反射率对数的倒数、反射率一阶微分、反射率倒数一阶微分为自变量的模型未通过P＜0.05的显著性检验。比较剩余7个模型的决定系数R2、均方根误差，并建立各模型松林郁闭度估测值与实测值的数学关系，比较其R2、E及平均估测精度，认为以反射率二次方根一阶微分为自变量对松林郁闭度有较理想的估测效果，模型表达式为：Y=0.062 8+59.724 0 X703.43-6.706 6X711.67，其后依次为：以反射率对数的倒数一阶微分、反射率、反射率二次方根、反射率对数、反射率倒数、反射率对数一阶微分为自变量的估测模型。

[1]许章华,龚从宏,刘 健,等.利用郁闭度与HJ-1多光谱数据估算马尾松林叶面积指数[J].植物资源与环境学报,2013,22(1): 29-35.

[2]Maynard D S, Ducey M J, Congalton R G, et al. Modeling forest canopy structure and density by combining point quadrat sampling and survival analysis[J]. Forest Science, 2013, 59(6):681-692.

[3]许章华.马尾松毛虫害天基空间监测与预警技术研究[D].福州:福建农林大学,2013.

[4]李永宁,张宾兰,秦淑英,等.郁闭度及其测定方法研究与应用[J].世界林业研究,2008,21(1):40-46.

[5]Franklin S E. Discrimination of subalpine forest species and canopy density using digital CASI, SPOT PLA, and Landsat TM data[J]. Photogrammetric Engineering and Remote Sensing,1994, 60(10): 1233-1234.

[6]Baynes J.Assessing forest canopy density in a highly variable landscape using Landsat data and FCD Mapper software[J].Australian Forestry,2004,67(4):247-253.

[7]吴 飏,张登荣,张汉奎,等.结合图像纹理特征的森林郁闭度遥感估测[J].林业科学,2012,48(2):48-53.

[8]李宇昊,石 田.利用航空数码影像的色彩特征估测森林郁闭度[J]. 西北林学院学报,2014,29(1):148-154.

[9]雷 磊,塔西甫拉提·特依拜,丁建丽,等.实测高光谱和HSI影像的区域土壤盐渍化遥感监测研究[J].光谱学与光谱分析,2014, 34(7): 1948-1953.

[10]杜晓明,蔡体久,琚存勇.采用偏最小二乘回归方法估测森林郁闭度[J].应用生态学报,2008,19(2):273-277.

[11]郑冬梅,曾伟生,智长贵,等.三峡库区森林郁闭度的遥感定量估测[J].中南林业科技大学学报, 2013,33(9):1-4, 26.

Comparison analysis on estimation effects of pine forest canopy density with hyper-spectrum variety transformations

XU Zhang-hua1,2a, LIU Jian2a,b,3, YU Kun-yong2a,b,3
(1. College of Environment and Resources, Fuzhou University, Fuzhou 350116, Fujian, China; 2a. Fujian Provincial Key Laboratory of Resources and Environment Monitoring & Sustainable Management and Utilization; b. College of Forestry, Fujian Agriculture and Forestry University, Fuzhou 350002, Fujian, China; 3. Sanming University, Sanming 365000, Fujian, China)

Based on the 60 groups (data group) of pine forests canopy density and hyper-spectrum data collected in Changting County,Jianyang District and Yanping District, the measured hyper-spectral reflectance data was transformed with variety methods. According to the top two correlation bands with pine forests canopy density by Gray Correlation Analysis, the pine forests canopy density estimation models were respectively established whose independent variables were reflectance, reflectance secondary root, reflectance logarithm,reflectance reciprocal, reflectance reciprocal of logarithm, first-order differential of reflectance, first-order differential of reflectance secondary root, first-order differential of reflectance logarithm, first-order differential of reflectance reciprocal, first-order differential of reflectance reciprocal of logarithm. Then the model coefficients of determination (R2) and root mean square error (RMSE) were compared. The 20 another samples collected in Jiangle County and Huaan County set a validation group. The mathematical relationships between estimation pine forests canopy densities and measured canopy densities were constructed, and the average estimation accuracy of R2, RMSE were compared. The results show that with the first-order differential of reflectance secondary root as the independent variable, the pine forest canopy density got a good estimation effect, with average estimation accuracy of 85.57%, followed were those by independent variable was first-order differential of reflectance reciprocal of logarithm, reflectance, reflectance secondary root,reflectance logarithm, reflectance reciprocal, first-order differential of reflectance logarithm successively as the estimating model of independent variables, while the models whose independent variables were reflectance reciprocal of logarithm, first-order differential of reflectance, first-order differential of reflectance reciprocal had no ability for pine forests canopy density estimation.

pine forests; pine forest canopy density; hyper-spectrum data; hyperspectral transformation; estimation model

S771.8

A

1673-923X(2015)11-0038-05

10.14067/j.cnki.1673-923x.2015.11.008

2015-01-10

国家自然科学基金青年科学基金项目（41501361）；福建省资源环境监测与可持续经营利用重点实验室开放基金项目（ZD1403）；福州大学人才基金项目（XRC-1345）

许章华，讲师，博士

刘 健，教授，博士，博士生导师；E-mail：fjliujian@126.com

许章华,刘 健,余坤勇.高光谱多种变换对松林郁闭度的估测效果对比分析[J].中南林业科技大学学报,2015,35(11):38-42.

[本文编校：吴 毅]