新疆西伯利亚云杉生物量模型研究

张绘芳，高亚琪，李 霞，朱雅丽，地力夏提·包尔汉

（1.新疆林业科学院 现代林业研究所，新疆 乌鲁木齐 830000；2.新疆农业大学 草业与环境科学学院，新疆 乌鲁木齐 830052）

新疆西伯利亚云杉生物量模型研究

张绘芳1，高亚琪1，李 霞2，朱雅丽1，地力夏提·包尔汉1

（1.新疆林业科学院 现代林业研究所，新疆 乌鲁木齐 830000；2.新疆农业大学 草业与环境科学学院，新疆 乌鲁木齐 830052）

基于50株样木的实测数据，运用相关分析和回归分析方法，采用四种模型构建了西伯利亚云杉的地上、地下和各组分器官的生物量估测模型，对比分析了各拟合结果得出以下结论：各生物量模型对比得知，地上和树干生物量模型估计精度均高于树枝、树叶和地下生物量模型；最优的二元模型拟合度和预估精度都优于一元模型，其中地上和树干生物量二元模型精度提高显著；树枝、树叶和地下生物量模型二元模型精度提高有限，建议实际应用时采用一元模型W=aDb。各生物量二元模型拟合优度和预估精度对比分析显示，不同的变量组合拟合效果不同，常用变量D2H在估计树枝、树叶生物量时效果不如一元模型精度，而变量D3/H对树枝树叶生物量的估计最有效。

新疆西伯利亚云杉；生物量估测模型；新疆阿尔泰山地

森林生态系统是陆地生态系统的主体，在应对全球气候变化和碳平衡等方面发挥着重要作用[1-3]。森林生物量是森林生态系统的基本数量特征，也是森林固碳能力的重要指标，对研究森林生态系统生产力、碳储量和碳循环具有重要的意义[4-5]。因此，开展森林生物量的监测和评估，准确估算森林生物量成为当今研究的热点之一。

森林生物量的获得关键在于林木生物量的准确测定和估计。目前应用较广泛的方法是生物量模型估计法，该方法是利用林木易测因子来推算难于测定的林木生物量，从而减少测定生物量的外业工作。首先，需要测定一定数样木生物量的数据，然后运用数学方法建立模型，模型一旦建立通过检验后，就可以在同区域或是同类的林分中来估计森林生物量，且有一定的精度保证[6-17]。

许多学者对林木生物量模型估计法做了大量的研究，曾伟生、张会儒、唐守正等[1-5，8-9]对立木生物量建模中回归模型的偏差校正、模型评价、相容性模型构建方法等做了研究，骆期邦等[16]对比分析了江西杉木、马尾松、阔叶树3个树种的线性和非线性的地上生物量模型，提出了适合该区域森林地上生物量估计的有效模型；陈振雄[14]采用分级联合控制和度量误差模型方法，建立云南云杉相容的立木生物量模型；杨阳等[23]采用实地调查与建模相结合的方法，建立了云南松各器官( 叶、枝、干、根)的生物量；王燕[19]利用相对生长率建立了枝基径和枝重间的回归关系，对天山云杉林的生物量和生产力进行了测定；李燕等[20]分别对杉木幼、中、成和不分林龄的单木各器官和全株生物量进行拟合比较分析。但是，基于实测数据构建新疆云杉生物量模型并检验其精度的研究尚未见报道。该研究以新疆西伯利亚云杉为研究对象，建立云杉地上和地下生物量模型，为制定云杉林生物量计量标准、开展全疆森林生物量资源清查和监测以及评价森林质量提供科学依据。

1 基础数据的采集与处理

研究所用数据为立木生物量实测样木数据，数据分别于2012年和2013年7～9月采集于阿尔泰山地，根据林分郁闭度按径阶选取，标准样木计50株，每个建模总体的样木数都均匀分配在2，4，6，8，12，16，20，26，32 及 38 cm 以上 10 个径阶，每个径阶的样木数也均匀分配在2～4 个树高级内，分别获取树干、树枝、树叶和树根的数据。

表1 实测样木株数及径阶分布Table 1 Tree numbers of measured sample wood diameter distribution class distribution

地上生物量测定采取全称重法，每株样木都实测胸径、树高，分别取树干、树枝、树叶称其鲜质量。树干按上（5/10H以上）、中(2/10H-5/10H)、下(0/10H-2/10H)3 个部分称其鲜质量，再分别在1/10、3.5/10、7/10 树高处各取2个圆盘样品，准确测定每个圆盘的鲜质量，再将树皮剥离后称树皮鲜质量；树冠分上、中、下3层，先将死枝挑选出来称其重量，然后分别称各层活枝的鲜质量，并分层各抽取3 个标准枝测定枝、叶比例，再在各层标准枝（不含叶）和全部标准枝的树叶中抽取含水率测定样品[3]。把样品带回实验室，在105℃的恒温下将样品烘干至恒质量，称干质量。以样木为单位，根据样木各区分段样品的干质量和鲜质量，计算相应的含水率，推算出样木各个区分段树干、树枝、叶的绝对干质量，各个区分段绝对干质量之和为样木地上部分总生物量。地下生物量采用全挖法将整个根系挖出，分根茎、粗根（≥ 10 mm）、细根（＜10 mm，不含2 mm以下须根）称鲜质量，同样分别选取代表性样品准确称其鲜质量，测定含水率，并推算得到地下部分生物量[21]。

2 模型构建与评价

立木生物量模型概括起来有3 种基本类型：线性模型、非线性模型、多项式模型，非线性模型的应用最为广泛,常用的模型变量有：胸径（D），D2，树高（H），D2H，也有的模型加上树龄、树冠等变量。实际中采用较多的生物量回归模型有：

公式（1）基于胸径D的一元模型，在国内外得到广泛应用，公式（2）、（3）基于胸径、树高的二元模型，是生物量估计中常用模型[5]，曾伟生根据连清生物量调查数据建立杉木、马尾松、云南松、湿地松和油松5个树种的模型对比分析中提出D3/H组合变量更适合树冠、树枝和树叶生物量模型，再由相关性分析得知D3/H与树枝、树叶和地下生物量相关性较高。因此本文以模型（1）、（2）、（3）分别构建云杉地上生物量、地下生物量和各组分器官生物量，对于树枝、树叶和地下生物量外加一个模型：

运用SPSS20.0进行分析构建模型参数，然后计算各个评价指标，根据评价指标分析确定每个组分的最优模型模型。

建立生物量回归模型，一般包括建模样本采集、模型结构确定、模型参数求解和模型检验评价，而对模型进行全面评价是建模的一个重要环节，对模型是否需要进行适应性检验是一个存在争议的问题。曾伟生（2011）以东北落叶松和南方马尾松的立木生物量模型的优度评价和精度分析中，通过蒙特卡罗模拟进行随机再抽样检验，印证了利用全部样本( 不分建模样本和检验样本) 来建立模型，它能充分利用样本信息，使模型的预估误差达到最小[9]。

因此，本研究为了充分利用实测数据建立模型，运用评价指标来判定模型的优度和精度，据参考文献[4-14]综合考虑以确定系数（R2）、估计值的标准误差（SEE）、总相对误差（TRE）、平均系统误差（MSE）、平均预估误差（MPE）5项作为模型评价的统计指标 。其计算公式[7-8]如下：

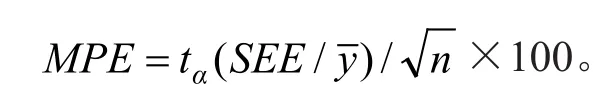
式中，yi为实际观测值；为模型预估值；为样本平均值；n样本单元数；p为参数个数；tα为置信水平α时的t值。在这5项指标中，R2和SEE 是回归模型的最常用指标，反映了模型的拟合优度；TRE和MSE是反映拟合效果的重要指标；MPE 是反映回归模型预估精度大小的重要指标[9]。

3 结果与分析

3.1 西伯利亚云杉生物量模型拟合结果分析

以阿勒泰地区50株标准样木实测数据为基础数据，以非线性模型W=aDb、W=a(D2H)b、W=aDbHc和W=a(D3/H)b为基础，分别运用曲线估计的回归方法和非线性回归迭代法建立云杉地上生物量和各组分器官生物量模型，然后进行对比，筛选出最优模型。拟合结果及统计评价指标见表2。

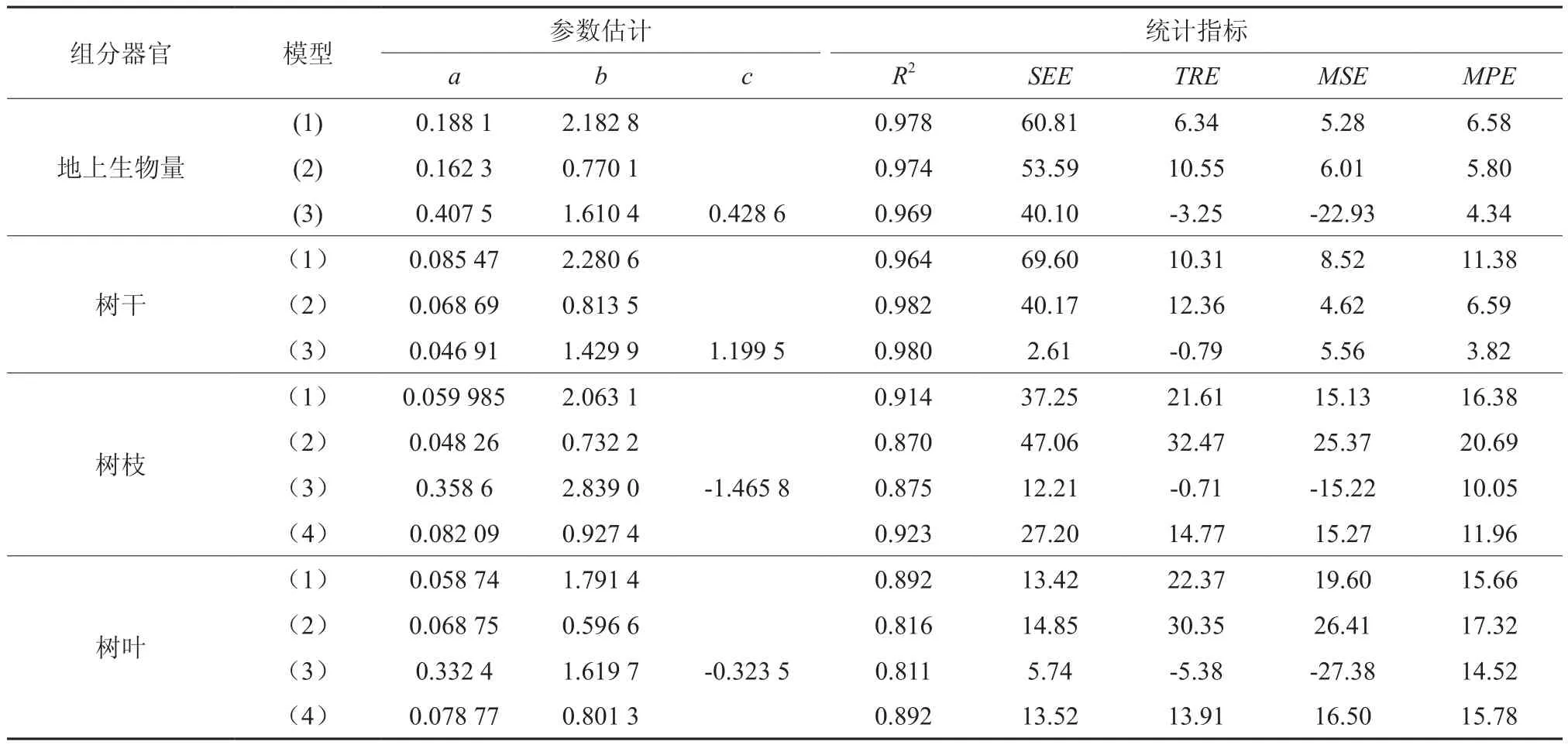
表2 西伯利亚云杉地上生物量和各组分器官生物量模型拟合结果Table 2 Model fitting results of aboveground biomass and each component organ biomass of P. obovata

表2看出，地上生物量和树干生物量的3种模型R2都超过0.96，说明这3种模型可以解释西伯利亚云杉地上生物量和树干生物量变动的96%以上， 但以拟合效果评价指标SEE、TRE和MSE、预估精度指标MPE对比不难发现，地上生物量和树干生物量模型从一元提升到二元，估计值的标准误差、总相对误差、平均预估误差等指标均有一定程度的上升，模型预估精度有较大改进，其中模型W=aDbHc的拟合效果最好，预估精度最高，达到95%以上；树枝、树叶生物量4种模型各评价指标显示，模型（1）决定系数R2相对较高，预估精度在83%以上，模型（2）决定系数、拟合优度和预估精度均低，模型（3）预估精度在85.48%，标准误差和总平均误差都减小，但决定系数最低，模型（4）的决定系数R2最高0.892，预估精度在84.22%以上，相对较高，结果表明树枝树叶生物量估计效果模型（4）最好，模型（1）次之，自变量因子的增加提高了模型的估计精度，但改进效果不显著；模型（2）估计效果最差，说明变量因子组合D2H不适合估计树枝和树叶生物量。

3.2 一元、二元模型相对残差分析

模型W=aDb的残差分析如图1所示。

图1可以看出，地上总生物量和各组分器官生物量模型的相对残差的散点各径阶随机分布，并且没有发生较大的发散现象，说明一元模型W=aDb的估计效果良好。

图1 一元模型W=aDb相对残差Fig.1 Relative residuals of single-factor model W=aDb

西伯利亚云杉各组分生物量一元模型如下：

W干=0.085 47D2.2806；

W枝=0.059 985D2.0631；

W叶=0.058 74D1.7914；

W地上总=0.188 1D2.1828。

模型W=aDbHc的残差分析如图2、3所示。

图2 二元模型W=aDbHc相对残差Fig.2 Relative residuals of two-factor model W=aDbHc

图2、图3可以看出，地上总生物量和树干生物量模型的相对残差的散点各径阶随机分布，并且没有发生较大的发散现象, 随着径阶增大误差值越小，说明估计效果良好；树枝和树叶生物量相对残差图显示模型W=aDbHc在胸径20 cm径阶以下预测值偏大，误差偏大，胸径20 cm径阶以上残差值呈均匀分布，误差较小，说明这个模型估计树枝树叶生物量有偏；树枝、树叶生物量模型W=a(D3/H)b的相对残差的散点各径阶随机分布，没有发生较大的发散现象，从残差分析说明模型W=a(D3/H)b的拟合树枝和树叶的生物量效果更好。

图3 二元模型W=a(D3/H)b相对残差Fig.3 Relative residuals of two-factor model W=a(D3/H)b

西伯利亚云杉各组分生物量最优二元模型如下：

W干=0.046 91D1.4299H1.1995；

W地上=0.646D1.6104H-0.4295；

W枝=0.082 09(D3/H)0.9274；

W叶=0.078 77(D3/H)0.8013。

西伯利亚云杉各部分生物量模型对比发现，地上生物量和树干生物量拟合以二元模型W=aDbHc为最优，树枝和树叶生物量模型以W=a(D3/H)b为最优，但一元模型地上生物量预估精度为93.42%，树干、树枝和树叶生物量预估精度为84%以上，TRE、MSE都小于25%，说明用一元模型来估计本区域云杉地上总生物量也是合适的。在实际工作中，考虑野外测量树高会加大工作量，且树高测定也会带来一定的测量误差[8]，在实践中估计西伯利亚云杉各部分生物量可以考虑采用一元模型，如果要得到更高精度的预估值，则可以采用二元模型。但是树叶生物量估计由于二元模型相比一元模型精度相当，均为84%，建议实际应用时采用一元模型W=aDb。

3.3 西伯利亚云杉地下生物量模型构建

运用阿尔泰山地50株标准样木的实测根数据，按照类似地上生物量的建立地下生物量的一元和二元非线性模型，参数估计和统计指标见表3。

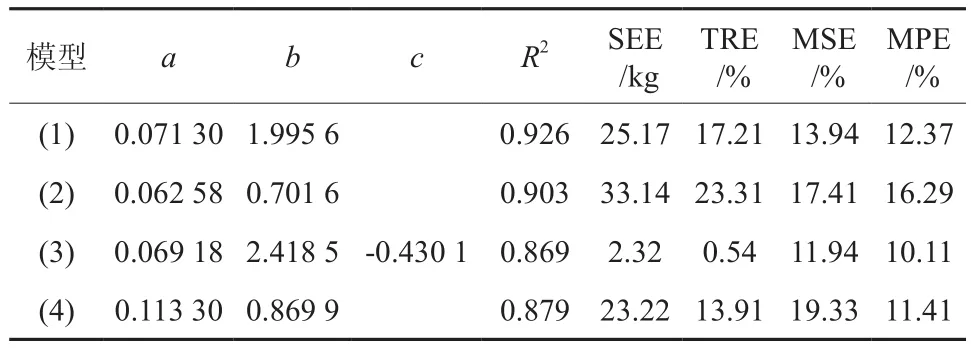
表3 西伯利亚云杉地下生物量模型拟合结果Table 3 Model fitting results of underground biomass of P. obovata

如表3所示，地下生物量四种模型中一元模型决定系数R2最高，达到0.926，对比评价指标SEE、TRE、MSE、MPE发现，模型（3）的拟合度最好，预估精度最高，89.89%，相对一元模型（1）预估精度提高了2.26%，改进效果不明显，而且决定系数反而降低了0.057，说明一元估计模型（1）比较稳定；模型（2）预估精度最低，说明变量组合D2H不适合地下生物量的估计。从模型（1）和（3）的相对残差图4、图5看出，两种模型的残差呈随机分布，说明估计效果良好，而且在实际工作中，考虑野外测量树高会加大工作量，且树高测定也会带来一定的测量误差。因此，西伯利亚云杉地下生物量最优估算为一元模型： W=0.071 3D1.9956。

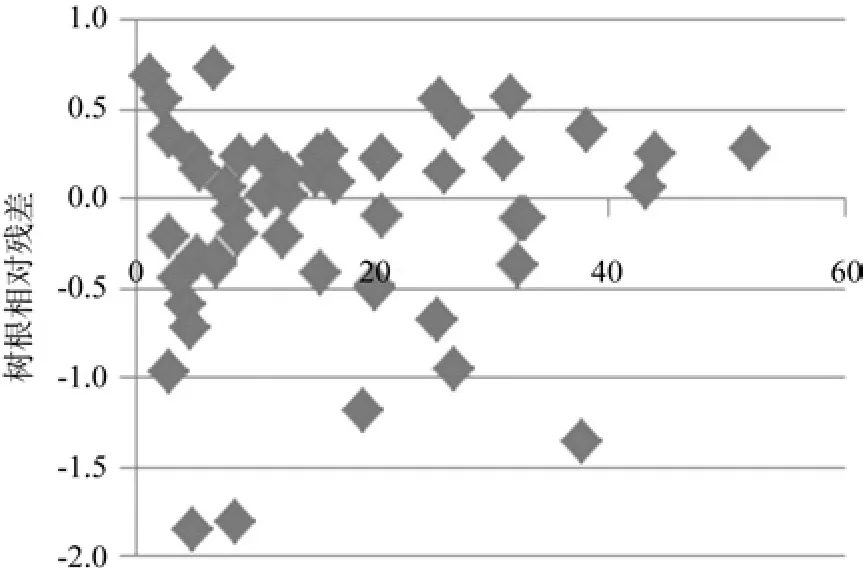
图4 一元模型W=aDb相对残差Fig.4 Relative residuals of single-factor model W=aDb

图5 二元模型W=aDbHc相对残差Fig.5 Relative residuals of two-factor model W=aDbHc

4 结论与讨论

本文基于50株标准样木实测数据，通过四种模型拟合西伯利亚云杉地上、地下和各组分器官的生物量估测模型，对比分析了得出以下结论：

(1)地上和树干生物量模型估计精度明显高于树枝、树叶和地下生物量模型。模型中选用常规调查因子胸径D和树高H与树干生长密切相关，所以其生物量模型估计精度高，针对更适合云杉树枝树叶和地下生物量模型的变量或变量组合还需要进一步研究。

(2)最优的二元模型拟合度和预估精度都优于一元模型，立木的生长受多种因素影响，自变量的增加能更好的解释其生物量的变化。其中一元到二元精度的提高，树干和地上生物量比树枝、树叶和地下生物量显著，说明树高因子对树干和地上生物量变化贡献较大。

(3)各部分生物量二元模型拟合优度和预估精度对比分析显示，不同的变量组合拟合效果不同。树干和地上生物量二元模型（3）采用与材积式相似的表达式对生物量的预估精度更高，树枝、树叶生物量模型以变量D3/H的模拟效果较好，D2H变量组合的估计精度反而不如一元模型，与曾伟生[5]分析杉木、马尾松、云南松、湿地松和油松生物量模型的结论一致，因此不同部位的生物量需要选择合适的变量或是变量组合解释。

(4)在实际工作中，考虑野外测量树高会加大工作量，且树高测定也会带来一定的测量误差[8]，因此建议在实践中西伯利亚云杉地上生物量和树干生物量，可以考虑采用一元模型，如果要得到更高精度的预估值，则可以采用二元模型，但是树枝、树叶和地下（树根）生物量估计由于二元模型相比一元模型精度提高有限，建议实际应用时采用一元模型W=aDb。

[1]曾伟生,唐守正,黄国胜,等.全国立木生物量建模总体划分与样本构成研究[J].林业资源管理,2010,(3):16-23.

[2]国家森林资源连续清查森林生物量模型建立暂行办法(试行).

[3]曾伟生.立木生物量建模样本数据采集方法研究[J].中南林业调查规划,2010,(2):1-6.

[4]王轶夫,孙玉军. 马尾松生物量模型的对比研究[J].中南林业科技大学学报,2010,30(10):29-33.

[5]曾伟生. 3种异速生长方程对生物量建模的对比分析[J].中南林业调查规划,2014,(1):1-3.

[6]董利虎,李凤日,贾炜玮.黑龙江省红松人工林立木生物量估算模型的研建[J].北京林业大学学报, 2012,(6):16-22.

[7]李智华.西北地区山杨立木生物量模型研建[J].四川林业科技,2013,(4):55-58.

[8]曾伟生,张会儒,唐守正.立木生物量建模方法[M].北京:中国林业出版社,2011:10-13.

[9]曾伟生,唐守正.立木生物量方程的优度评价和精度分析[J].林业科学,2011,(11): 106-113.

[10]付 尧,马 炜,王新杰,等.小兴安岭长白落叶松相容性生物量模型的构建[J].东北林业大学学报,2011,39(7):42-45.

[11]胥 辉.一种生物量模型构建的新方法[J].西北农林科技大学学报:自然科学版,2001,29(3):35-40.

[12]王苏颖.云杉林生物量空间异质性研究[R].福建师范大学,2010.

[13]罗云建,张小全,王效科,等.森林生物量的估算方法及其研究进展[J].林业科学,2009,(8):129-134.

[14]陈振雄,贺东北,甘世书.云南省云杉立木生物量模型研建[J].中南林业调查规划,2011,(4):56-61.

[15]曾伟生.我国杉木通用性立木生物量模型研究[J].中南林业调查规划,2013,(4):4-12.

[16]骆期邦,曾伟生,贺东北,等.立木地上部分生物量模型的建立及其应用研究[J].自然资源学报,1999,(7):271-277.

[17]胥 辉.林木生物量模型研究评述[J].林业资源管理,1997,(5): 33-36.

[18]许俊利,何学凯.林木生物量模型研究概述[J].河北林果研究,2009,(2):141-145.

[19]王 燕,赵士洞.天山云杉林生物量和生产力的研究[J].应用生态学报,1999,10(4):389-391.

[20]李 燕,张建国,段爱国,等.杉木人工林生物量估算模型的选择[J].应用生态学报,2010,21(12) :3036-3046.

[21]尹艳豹,曾伟生,唐守正.中国东北落叶松立木生物量模型的研建[J].东北林业大学学报, 2010,38(9):42-45.

[22]金钟跃,贾炜玮,刘 微.落叶松人工林生物量模型研究[J].植物研究,2010,30(6): 747-752.

[23]杨 阳,冉 飞,王根绪,等.西藏高原云南松生物量模型及碳储量[J].生态学杂志,2013,32(7):1674-1682.

[24]付 尧,马 炜,王新杰,等.小兴安岭长白落叶松相容性生物量模型的构建[J].东北林业大学学报,2011,39(7):23-26.

Research on biomass model of Picea obovata in Xinjiang

ZHANG Hui-fang1, GAO Ya-qi1, LI Xia2, ZHU Ya-li1, Dilixiati Baoerhan1
(1.Modern Forestry Research Institute of Xinjiang Academy of Forestry, Urumqi 830000, Xinjiang, China;2. College of Grassland and Environment Sciences, Xinjiang Agricultural University, Urumqi 830052, Xinjiang, China)

Based on the measured data of 50 sample trees, using correlation analysis and regression analysis methods, and by adopting four kinds of methods, the biomass estimating models for ground, underground, and each component organ of Picea obovata were constructed. The fitted results of set models were compared. The results show that contrasted all the biomass models, the estimated accuracy values of ground and trunk biomass models were higher than those of branches, leaves and underground biomass models; the optimal binary model’s fitting degree and forecast accuracy both were superior to single-factor model, of them the ground and trunk biomass binary models improved significantly in accuracy, the accuracy values of the binary model of branches, leaves and underground biomass model had a limited increase, so it is suggested that in the actual application, the W=aDbmodel should be used. The comparative analyses on biomass of two element model goodness of fit and predictive accuracy show that with different combinations of variables,the fitting effects were different, the effects of common variables (D2H) used in estimating branches and Leaf biomass were not as good as that of single-factor model, while the variable (D3H) had the most effective to estimating branches, foliage biomass.

Picea obovata; biomass estimation model; Altai Mountains in Xinjiang

S791.18

A

1673-923X(2015)11-0115-06

10.14067/j.cnki.1673-923x.2015.11.021

2015-01-10

新疆林业厅项目新疆林业数表构建项目；国家国际科技合作项目（2010DFA92720-15）；新疆维吾尔自治区公益性科研院所基本科研业务经费资助项目

张绘芳，助理研究员

高亚琪,研究员；E-mail：lkyxds@163.com

张绘芳，高亚琪，李 霞，等. 新疆西伯利亚云杉生物量模型研究[J].中南林业科技大学学报, 2015, 35(11): 115-120.

[本文编校：吴 毅]