铁矿石等温气固还原动力学研究

邵久刚，张建良，刘征建， 国宏伟， 杨广庆，王广伟

(1.北京科技大学 冶金与生态工程学院，北京 100083；2.河北联合大学 冶金与能源学院，河北 唐山 063009)

铁矿石等温气固还原动力学研究

邵久刚1，张建良1，刘征建1， 国宏伟1， 杨广庆2，王广伟1

(1.北京科技大学 冶金与生态工程学院，北京 100083；2.河北联合大学 冶金与能源学院，河北 唐山 063009)

将未反应核模型拓展应用于烧结矿气相还原，采用四阶龙格库塔法通过编制程序求解混合控制方程.通过数值计算与实验数据的对比，证明烧结矿的气固还原过程和球团矿一样可以用未反应核模型来描述.烧结矿形状不规则，不具有明确的半径，通过与前人研究的比较，本文摒弃了传统处理中的平均半径选取，利用数据分析得到了适用于烧结矿的等效半径，解决了烧结矿应用未反应核模型时的半径选取问题，为铁矿气固还原动力学的研究提供了新的参考.

铁矿石；气固还原动力学；未反应核模型；等效半径

依托未反应核模型的铁矿气固还原动力学已经进行了诸多的研究[1～7]，以往的研究主要集中于球形颗粒，对于非球形颗粒如烧结矿的研究尚不完善；对于烧结矿等不规则形状颗粒是否符合未反应核模型亦未进行充分系统的论证.利用未反应核模型研究球形铁矿气固还原是一个比较成熟的过程，1983年李兰滨等人研究了CO-CO2混合气体逐段还原赤铁矿球团[1]，利用数值模拟得到了与实际实验结果相符合的结果.在文章中详细介绍了未反应核收缩模型的建立以及相应还原过程各个参数的确定和推导.

1998年Heung, Won, Takeaki等人发表了一系列论文[2～5]，详细论述了非球形颗粒气固还原动力学，但是非球形颗粒仍然仅限于长方体、圆柱体等规则形状，并未扩展到形状极不规则的烧结矿.1986年王希珍等人研究了高碱度烧结矿高温还原过程的动力学[6]，利用未反应核收缩模型分析了烧结矿的气固还原过程.试验用烧结矿原料半径在5～8 mm之间，在利用未反应核收缩模型处理时，还原半径采用的是平均法，即半径设为6.5 mm.研究发现，用平均法处理烧结矿半径并不科学，会对反应过程的计算产生重大影响.

本文利用某钢铁公司炼铁厂生产用的烧结矿和球团矿进行等温气固还原，通过实验数据确定相应参数.利用编程语言求解混合控速方程，通过参数录入计算整个还原历程.数值计算结果与实验数据一致，证明了处理方法的科学性.

1 实验部分

1.1 实验设备及原料

实验设备如图1所示，主要分为三个部分：1)加热设备为包头灵捷炉业有限公司生产的管式电阻炉，升温速率5 ℃/min，升温上限为 1 400 ℃；2)反应管内径为80 mm，还原气体由下部管道进入，样品在反应管中与还原气体混合反应，为保证气体预热和气流均匀在反应管底部装入一定量的刚玉球；3)天平，连续称取反应过程当中样品失重量. 实验原料为国内某钢铁企业生产使用的球团矿和烧结矿，其成分如表1所示.

1.2 实验过程

由于单个颗粒质量较小，利用单颗粒进行气固还原实验容易受到外界因素的干扰，使实验结果产生较大波动.为了减小波动，本实验采用多颗粒还原实验，利用平均法进行单颗粒分析.球团矿和烧结矿选取粒径控制在10～12 mm之间，实验当中球团矿选择粒度均匀、球形规则、表面无裂纹的颗粒，烧结矿为筛下随机选取.每次称取500±15 g样品放入反应管内，反应管与天平相接，悬挂于管式炉炉膛当中，调整天平高度使样品位于管式炉恒温区域，热电偶插入样品当中测取样品反应温度.实验开始后通氮气保护样品，管式炉升温速率5 ℃/min，温度升至900 ℃保温30 min后，通入CO与N2的体积比为3∶7混合气体，混合气体流量为15 L/min，样品当中每个颗粒周边的气氛基本相同，排除下部样品还原产物对上部样品反应的影响，利用天平实时记录炉料失重.

图1 中温管式炉示意图Fig.1 Schematic chart of the heating oven1-天平； 2-热电偶； 3-反应管； 4-矿石； 5-加热炉; 6-温控器

表1 原料化学成分/(质量分数)

2 模型及数据处理

利用单界面未反应核模型研究反应过程，浮士体的还原是整个还原过程的限制环节，反应方程为：

CO+FeO=Fe+CO2

(1)

由文献[8]中的热力学数据可以得出900 ℃下化学反应(1)的标准平衡常数为K0=0.593.由于实验过程当中反应管通过排气管与大气连接，内部压力与大气压力相同，为101.325 kPa.根据实验气体流量和反应管内径可以求出气相本体CO浓度是3.12 mol/m3，通过化学反应(1)900 ℃的平衡计算可以求得界面处化学反应平衡的CO浓度为1.99 mol/m3.

未反应核模型在气固反应计算当中的运用已经被众多学者所证明[1～6]，其积分形式可以表示为：

(2)

式中，r0为颗粒初始半径，m；d0为单位体积去除的氧原子浓度，mol/m3；Deff为有效扩散系数，m2/s；krea+为正反应速率常数；Cb为气相本体气体浓度，mol/m3；Ce为界面处平衡气体浓度，mol/m3；K0为反应标准平衡常数；XB为还原率，即质量损失/总的与Fe结合的氧的质量；kg为气相边界层传质系数，m/s.

当利用未反应核模型处理实验时，需要引入如下中间变量：

(3)

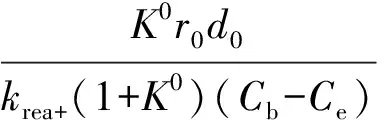
(4)

(5)

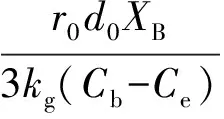
(6)

将式(3)、(4)、(5)和(6)带入式(2)，未反应核模型的积分形式可以简化得到：

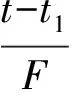
(7)

在传统计算中，气相边界层传质系数kg通过公式(8)计算得到:

(8)

式中:D为混合气体扩散系数，m2/s；Re为气体流动雷诺数；Sc为施密特准数.

式(8)属于经验公式，本身存在一定的误差，并且实际过程中混合气体扩散系数D以及Re、Sc两个准数的确定和计算都比较困难，所以通过该公式直接确定气相边界层传质系数kg会带来许多不确定性.本文利用实验数据，通过对模型进行数学处理确定kg的值.

2.1 球团矿

图2 球团矿作图法求反应速率常数和有效扩散系数Fig.2 Determination of krea+ and Deff of pellet

利用球团平均半径作为未反应核模型初始半径，即r=5.5 mm.在实验条件下只有与Fe结合的氧可以被还原，包括Fe2O3中的氧和FeO中氧.单个颗粒平均质量为3.46 g，结合原料成分可知单位体积可去除的氧原子浓度为d0=70 444 mol/m3.

由图可确定直线斜率A=360.2，截距B=8.944，结合公式(3)和公式(4)，求得900 ℃条件下球团矿CO还原过程有效扩散系数Deff=1.45×10-5m2/s，正反应速率常数krea+=0.231 m/s.

2.2 烧结矿

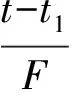
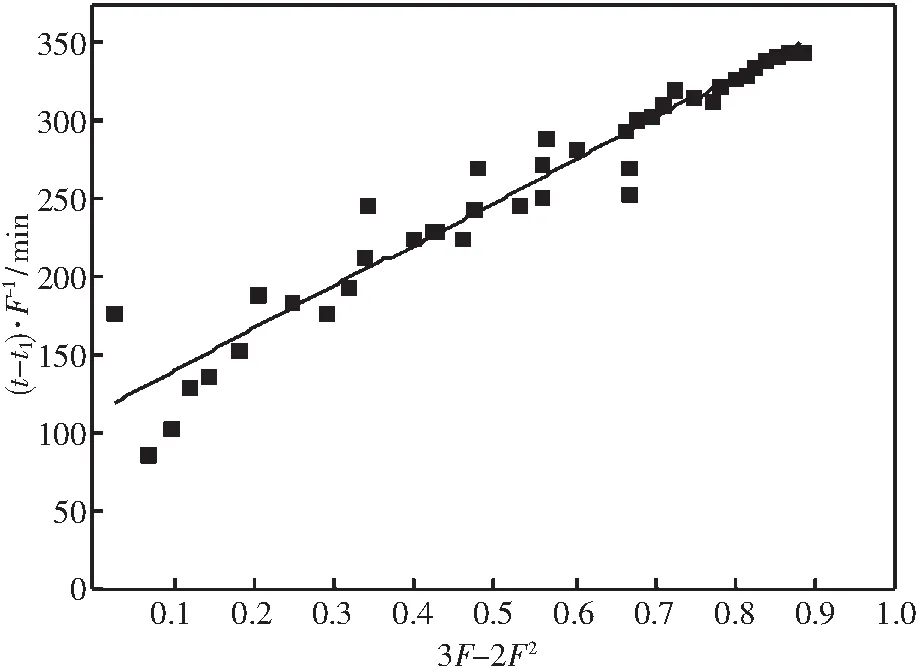
图3 烧结矿平均半径作图法求反应速率常数和有效扩散系数Fig.3 Determination of krea+ and Deff of sinter with average radius method

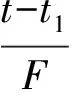
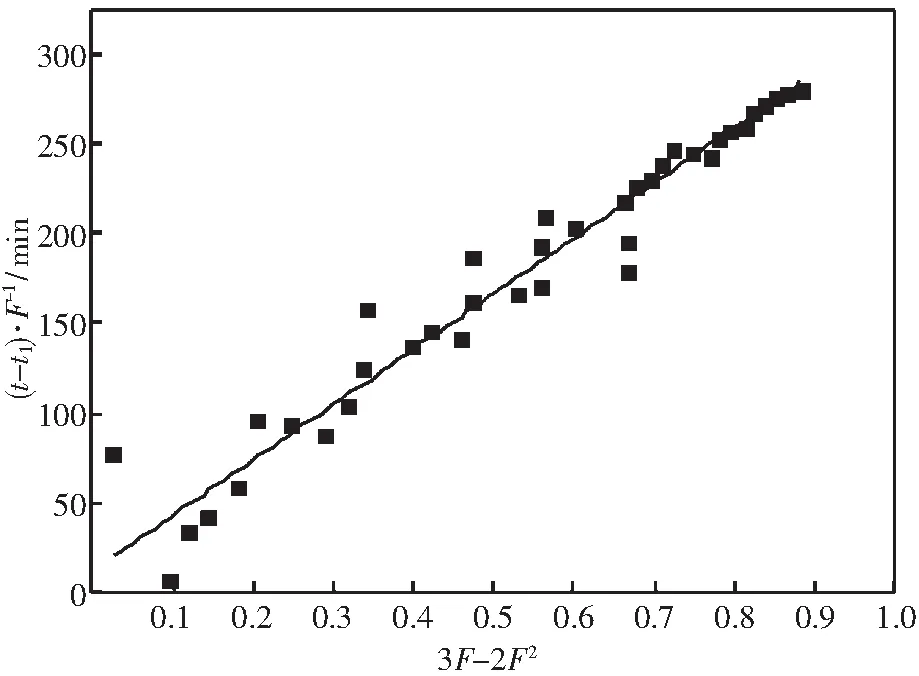
图4 烧结矿等效半径作图求反应速率常数和有效扩散系数Fig.4 Determination of krea+ and Deff of sinter with equivalent radius method

3 分析讨论

表2 未反应核模型参数

球团矿和烧结矿900 ℃，CO与N2的体积比为3∶7条件下，还原过程各个参数计算结果如表2所示：未反应核模型混合控速方程微分形式为[7]

(9)

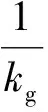
利用C++语言编制程序，采用四阶龙格库塔法求解方程，时间步长设为1 s.利用表2中的参数分别计算烧结矿和球团矿在整个还原过程当中还原率随时间的变化.计算结果如图5和图6所示.

图5 球团矿实验数据与程序计算结果比较Fig.5 Experimental and calculated result for pellet

图6 烧结矿实验数据与程序计算结果比较Fig.6 Experimental and calculated result for sinter

还原过程中各步骤阻力的变化如表3、4所示：

由各步骤阻力变化可知，反应前期为外扩散控制，中期为内扩散和外扩散混合控制，并且随着反应的进行内扩散阻力越来越大，后期主要为内扩散控制.整个反应过程化学反应阻力微小，没有对反应进程产生明显影响.

表3 球团矿各步骤阻力随时间变化

表4 烧结矿还原各步骤阻力随时间变化

球团矿选择的是球形标准无裂纹的颗粒，反应过程中反应界面收缩均匀，与未反应核模型假设一致，所以模型计算数据与实验数据达到了高度的一致.烧结矿虽然颗粒大小差别不大，但是不具有规则的形状，反应过程中反应界面收缩受局部形状因素的影响并不均匀，这与未反应核模型假设不一致，所以在反应过程的某个阶段才会出现上下波动.烧结矿实验数据与模型之间的波动只产生于反应中期，在初期和后期与球团矿一样达到了高度的一致.反应初始阶段受到外扩散控制，在采用等效半径后形状因素的影响被弥补，反应进程是由气相边界层传质系数决定的，所以理论计算与实验数据能够一致；反应后期已经形成了足够厚的产物层，内扩散阻力相对很大，这时候形状变化的影响相比之下微小，反应进程由产物层中的内扩散控制，所以理论计算与实验数据能够一致；在反应中期，反应进程受到外扩散和内扩散混合控制，并且产物层还不够厚，未反应核反应界面处局部形状的变化会对瞬时反应速率产生一定的影响，所以才会出现理论计算与实验数据之间的波动.

4 结 论

(1)建立了球团矿和烧结矿CO等温还原动力学模型，实现了对气固还原反应过程的准确计算.

(2)根据烧结矿的形状不规则的特性，提出了等效半径的概念，用于替代传统的筛分平均半径，计算结果证明，有效半径能够满足烧结矿还原过程中未反应核模型的应用.

(3)实验条件下，球团矿和烧结矿还原过程当中，前期为外扩散控制，随着反应进行内扩散阻力增大，最终是外扩散和内扩散混合控制，界面化学反应阻力在整个反应过程当中都比较微小.

[1] 李兰滨，黄履安，李万珍. 用CO-CO2混合气体逐段还原赤铁矿球团矿的还原反应速度[J]. 钢铁研究学报，1983，3(1)：1-8.

(Li Lanbin，Huang Luan，Li Wanzhen. Step-wise reduction rates of hematite pellets with CO-CO2Gas mixtures[J]. Journal of Iron and Steel Research，1983，3(1)：1-8.)

[2] Heung W K, Won S C, Takeaki M,etal. Effect of iron ore size on kinetics of gaseous redution[J]. ISIJ International, 1998, 38(2):109-115.

[3] Heung W K, Won S C, Takeaki M,etal. Gas-solid reaction model for non-spherical iron oxide[J]. ISIJ International, 1998; 38(4):324-329.

[4] Heung W K, Won S C, Takeaki M,etal. Effect of iron ore shape on gaseous reduction rate[J]. ISIJ International, 1998, 38(11):1194-1198.

[5] Heung W K, Won S C, Takeaki M,etal. Ishida-Wen’s model for non-spherical particle[J]. ISIJ International, 1998, 38(12):1304-1310.

[6] 王希珍，李宪文，周国凡，等. 高碱度烧结矿高温还原过程动力学研究[J]. 炼铁，1986，1(5):1-7.

(Wang Xi-zhen，Li Xian-wen，Zhou Guo-fan，etal. Study on dynamics of high temperature reduction of high basicity sinter ore[J]. Iron Making，1986，1(5):1-7.)

[7] 郭汉杰. 冶金物理化学[M]. 第2版，北京：冶金工业出版社，2006：114-126.

(Guo Han-jie. Physical chemistry of metallurgy [M]. Second Edition，Beijing：Metallurgical Industry Press，2006：114-126.)

[8] 何其松. 钛磁铁矿球团的还原历程及其热力学分析[J]. 钢铁，1983，18(4): 1-7.

(He Qi-song. Reduction of titanomagnetite and thermal dynamics [J]. Iron and Steel，1983，18(4)：1-7.)

Kineticsofisothermalreductionofironorebygas

Shao Jiugang1, Zhang Jianliang1， Liu Zhengjian1, Guo Hongwei1,Yang Guangqing2, Wang Guangwei1

(1.School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing，Beijing 100083, China；2. School of Metallurgy and Energy, Hebei United University, Tangshan 063009, China)

The gaseous reduction of the sinters by CO-N2at 900 ℃ was solved by an extended unreacted core model. The mix controlling equation was calculated through a four-order Runge Kutta method by using C++ programming language. Compared the calculated data with the experimental ones, it was proved that the gas-solid reduction of the sinters can be described by the unreacted core model as same as the pellet does. Owing to the anomal shape and the indefinite radius of the sinter, abandoning the traditional approach, the authors found an “equivalent radius” suitable to the sinter through data analysis. It’s believed that the authors’ finding will provide a new reference for this field.

sinter; gaseous solid reduction; unreacted core model; equivalent radius

10.14186/j.cnki.1671-6620.2015.01.006

2013-09-20.

国家重点基础研究发展计划资助(973 计划) (NO.2012CB720401 ):十二五国家科技支撑计划(NO. 2011BAC01B02)

邵久刚(1987-),男，博士研究生，E-mail：shaojiugang1987@163.com.

TF 55

A

1671-6620(2015)01-0024-05