基于自适应多种群遗传算法的可修医疗服务备件库存优化研究

刘绍锴，张方圆，朱海煜，段 磊，吴小玲，房 坤

基于自适应多种群遗传算法的可修医疗服务备件库存优化研究

刘绍锴，张方圆，朱海煜，段 磊，吴小玲，房 坤

目的：研究医疗器械行业中可修复的医疗服务备件的库存优化问题，为医疗服务备件库存策略提供指导。方法：在METRIC（multi-echelon technique for recoverable item control）可修服务备件的单个中心仓库二级库存模型基础上，采用数学建模方法建立可修医疗服务备件库存模型，采用自适应多种群遗传算法求解该模型。以医院医疗服务备件为背景，考虑多服务备件供应商、多区域维修中心及多维修站，以年预算为约束条件，建立以年缺货期望最小为目标的二级库存优化模型，设计了该模型求解的自适应多种群遗传算法，采用Matlab工具通过数值算例说明优化模型的正确性和算法的有效性。结果：自适应多种群遗传算法结合了自适应遗传算法和多种群遗传算法的双重优点，其结果优于这2种算法，有效解决了医疗服务备件库存成本问题。结论：采用数学建模和自适应多种群遗传算法能很好地解决可修复的医疗服务备件库存优化问题，研究结果对降低医疗可修服务备件库存成本、提高物流效益具有重要指导作用。

医疗可修服务备件；二级库存；METRIC模型；自适应多种群遗传算法

0 引言

随着现代医学技术特别是医疗设备的高速发展，医院呈现集团化、大规模化、区域分布化趋势，对医疗器械维修服务备件的库存需求也越来越大，原有的库存管理控制模式已经满足不了迅速增长的业务量的需求，供应商、区域维修中心和维修站的库存问题越来越严重，不仅占用了大量的资金，而且维修服务水平也无法保障。所以，为了降低库存成本，提高医疗企业的收益，改善客户服务水平，对医疗器械维修备件库存进行优化是非常有必要的。目前国内外学者从库存模型和模型求解算法2个方面对库存开展研究。

在库存模型研究方面，文献[1]考虑了一个后方仓库和多个基地，建立了一个二级库存模型，即MET-RIC（multi-echelon technique for recoverable item control）模型。Adams[2]致力于库存需求量的预测，主要是通过检验2种不同的备件分析和优化的方法，来决定预测初始库存需求量的最佳方法，并使用了备件优化技术量化风险和收益。文献[3]研究了药品供应链及其医药库存管理，建立了集成医药公司和医院的生产和流通的连续检测库存模型，该模型考虑了药品订购的提前期和延期支付问题。针对三级供应链，文献[4-5]研究了位置-库存模型，该模型考虑直销仓库中心位置、流量分配和装载量3个决策变量，文献[6]在METRIC模型的基础上建立了新的库存模型，并采用自适应遗传算法求解模型。METRIC模型是只考虑了一个后方仓库和多个基地的库存模型，本文在前人[6]的基础上考虑了多区域维修中心和多二级维修站的医疗可修服务备件的库存，建立相应的模型。

在库存模型求解算法研究方面，文献[7-8]将改进的自适应遗传算法应用到混凝土行业的库存系统仿真模型，在原有遗传算法的基础上，又进行了改进，得出了新的自适应遗传算法，并运用在电力系统的优化中，所得结果良好。由于自适应遗传算法能以较大的概率避免算法陷于局部最优解，且多种群算法通过多个种群在进化过程中进行信息交换，最终的最优解是多个种群协同进化的结果，所以，本文采用多种群遗传算法和自适应遗传算法相结合的自适应多种群遗传算法求解库存模型。

1 物理模型

METRIC模型是由单个供应商、单个区域维修中心和多个维修站组成，如图1中虚线所示。本文考虑医疗器械供应、维修和使用机构的区域分布性，在METRIC模型的基础上，将备件供应商、区域维修中心和维修站扩展到多个，以适应现代医疗备件的维修分布式库存需求，构建包括备件供应商、区域维修中心和维修站的医疗可修服务备件多级库存物理模型，该模型是由s个各不相同的备件供应商、n个不同的区域维修中心和维修站组成，而每个区域维修中心服务m个相同的维修站，其物理模型如图1所示。

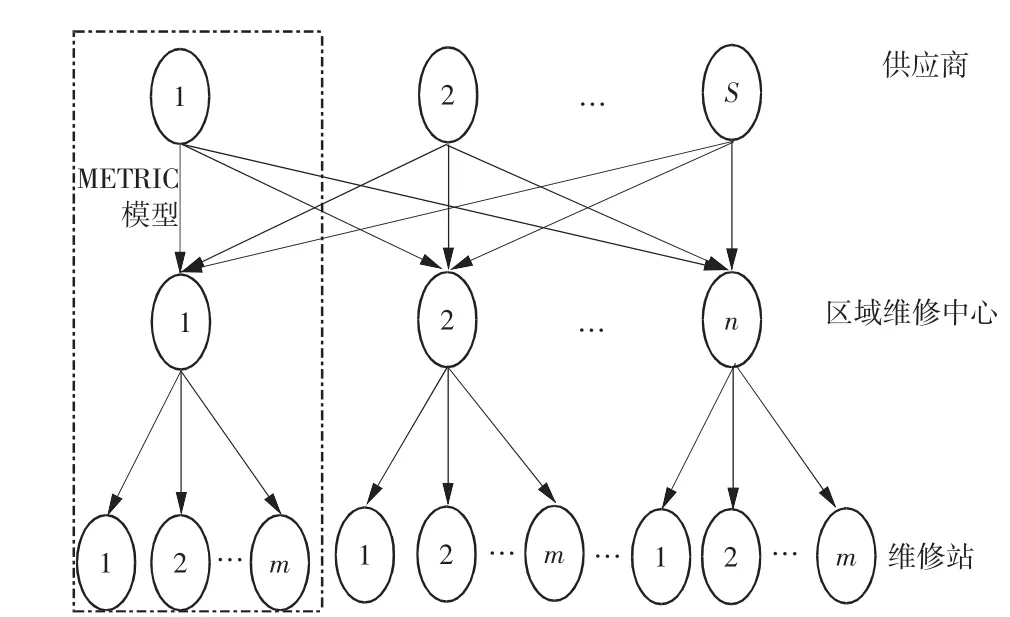
图1 医疗服务备件库存物理模型

医疗可修服务备件修理的物理过程可表述如下：

当维修站遇到需修理的备件时，先自行维修，若是该级不能实现备件维修则交给上级区域维修中心进行维修。上级能实现备件维修的，修好并返回给下级或者留作当地库存；不能维修的备件，返回供应商维修。当区域维修中心的备件不能满足需求时，请求供应商供应。本文中假定供应商的维修能力和供应能力是能满足医疗服务备件维修需求的。当上一级收到下一级的供货申请时，从下一级发出供货申请到获得备件的时间即为订货和运输时间。且设定文中备件费用只考虑零部件本身的价格、库存费用等，其他相关费用忽略不计。

2 数学模型

根据以上物理模型，可修服务备件库存数学模型包括区域维修中心的库存控制模型和二级维修站的库存控制模型。

2.1 区域维修中心的库存控制模型

由Palm定理可知：若一项备件的需求服从年需求均值为y的泊松过程，且每一故障备件的修理时间相互独立，并服从均值为T年的同一分布，则在修理件的稳态概率分布服从均值为yT的泊松分布[8]。

区域维修中心对服务备件的年平均需求量yjk是其服务的维修站的年平均需求量yijk之和，表达式如式（1）：

其中，i为第i个维修站，i=1，2，…，m；k为第k种服务备件，k=1，2，…，h；j为第j个区域维修中心，j= 1，2，…，n；r为服务备件k在维修站被维修的概率，相对应地，送到区域维修中心维修的概率是1-r。

区域维修中心的供应渠道平均数wjk为

根据Palm定理得到第j个区域维修中心对第k种服务备件需求量Xjk可修备件的概率为

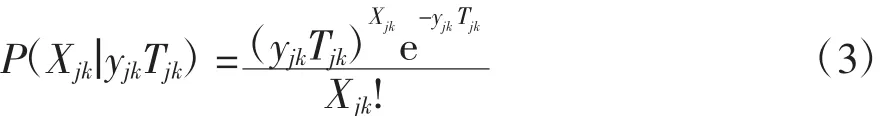
其中，Tjk为服务备件k在区域维修中心的平均修理时间。

由公式（2）和（3），得出区域维修中心j中服务备件k的缺货量Bjk的缺货期望为

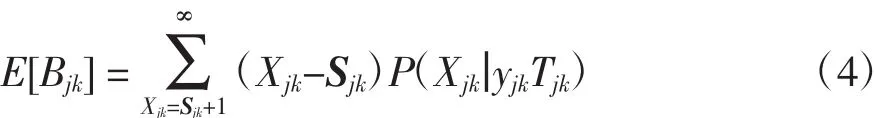
2.2 维修站的库存控制模型

因维修站缺货而导致的平均延误时间t为

从而，二级维修站的供应渠道平均数为

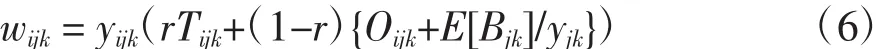
其中，Oijk为区域维修中心与维修站之间从订货到交货的平均时间（年）。

由Palm定理可知，维修站i可提供服务备件需求量Xijk个可修备件的概率为

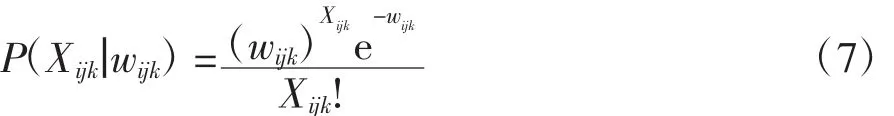
则区域维修中心j对应的第i维修站的服务备件k的缺货量Bijk的缺货期望为

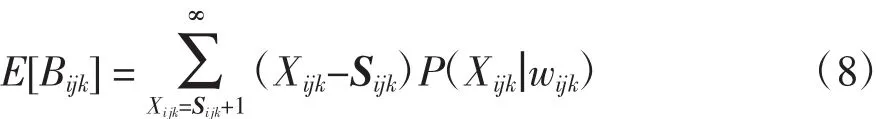
所建模型的目标函数为区域维修中心和维修站的最小期望缺货量B，约束条件为区域维修中心和维修站对k种可修服务备件的年库存总预算C。数学模型表达如下：

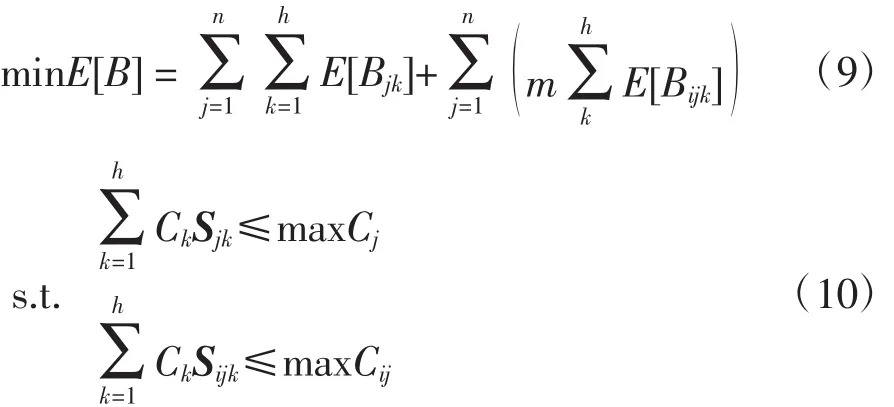
对目标函数进行如下分析：

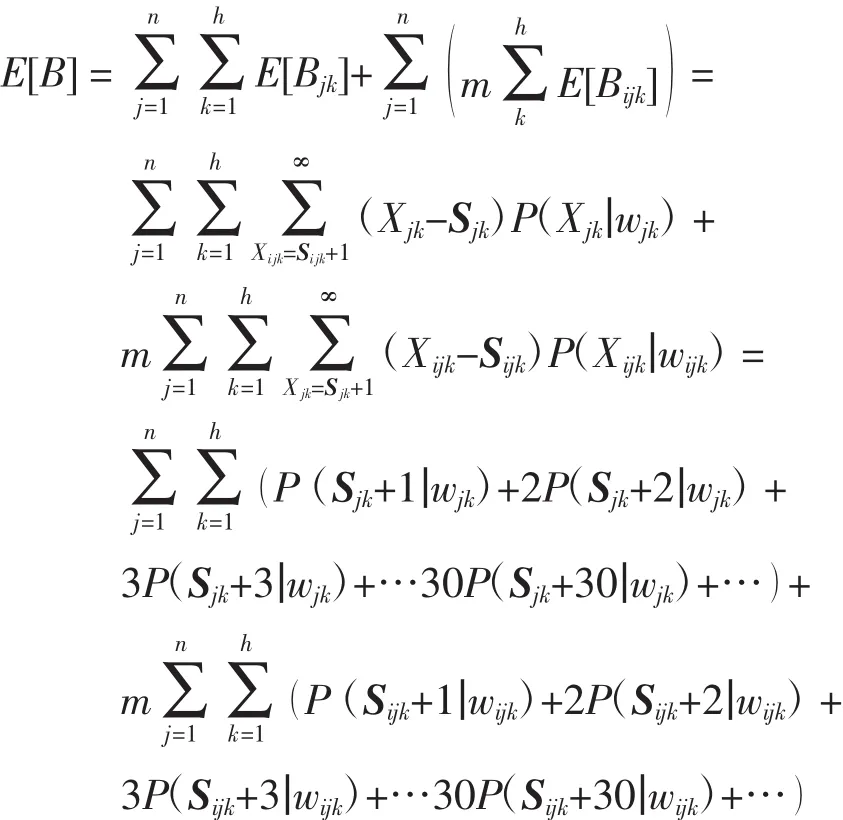
其中，n为区域维修中心的数量，h为服务备件的数量，m为维修站的数量；Ck为可修服务备件k的单价，maxCj为区域维修中心j的年预算，maxCij为第j个区域维修中心服务的第i个维修站的年预算；Sjk为区域维修中心k种备件库存量；Sijk为维修站i的k种备件库存量。

由泊松分布的概率函数的单调性可知E[B]存在最小值，在上述表达式中，当S趋于无穷大时，E[B]趋于0，与现实相符，即当库存足够时，则不存在缺货。又由于要满足约束条件，可以找到S，使得E[B]最小。

3 自适应多种群遗传算法

目标函数为非线性函数时，用其他优化方法较难求解，而利用遗传算法求解能得到较好的结果。本文分别采用自适应遗传算法、多种群遗传算法、自适应多种群遗传算法求解模型。由于自适应多种群遗传算法是前2种算法的综合，故本文只给出自适应多种群遗传算法，具体步骤如下：

（1）初始化。

将区域维修中心的库存变量表示为

维修站的库存量变量表示为

并初始化算法的各种控制参数。

（2）产生初始种群。

在给定的可行取值范围内，采用二进制编码，随机为每个种群产生个体，创建MP个初始种群。

（3）计算适应度函数。

采用罚函数法进行处理，得到适应度函数[6]为

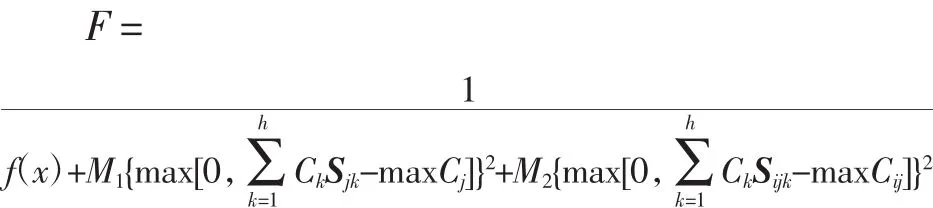
其中，M1、M2表示无穷大的常数。利用Matlab遗传算法工具箱，则适应度函数为Fit（n）=ranking（-F）。

（4）选择复制。

采用轮盘赌方法，以种群的适应度函数计算出的个体适应度为依据准则，选择部分个体。

（5）交叉和变异。

在求解过程中，对交叉和变异概率进行自适应调整，使每个个体按照适应度大小，选择不同的交叉和变异概率，自适应交叉和变异概率分别由以下2个公式求解：

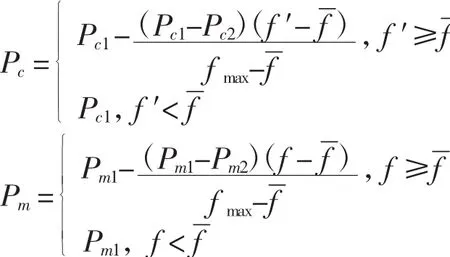
其中，Pc1和Pc2为交叉算子控制参数；Pm1和Pm2为变异算子控制参数；fmax为种群中最大的适应值为每代群体的平均适应值；f为变异的个体适应值；f′为2个交叉的个体之中较大的那个适应值。

（6）移民操作。

每隔一定代数，将进化中种群的最优个体移民到其他种群中，即替换掉其他种群中的最差个体。

（7）精英保留操作。

在每一代进化过程中，将种群的最优个体保存到一个精英种群中，及时更新最优个体。

（8）判断终止条件。

判断最优个体是否达到最少保持代数，若满足终止判断条件则输出所求最优解，如果没有，则转到步骤（3）继续循环进化，直至满足条件。

4 实例分析

4.1 案例

某医疗企业有3个区域维修中心，每个区域维修中心服务4个维修站，订购的备件有6种。3个区域维修中心、维修站及其6种服务备件的年需求量为yijk，平均修理时间Tijk、Tjk以及服务备件维修的概率r分别见表1～3。备件1～6的单价依次为1 220、1 780、450、1 250、3 000、1 870元，区域维修中心与维修站之间从订货到交货的平均时间Oijk=0.01，区域维修中心和其服务的维修站的可修服务备件库存年预算分别为maxCj=120 000元、maxCij=36 000元。

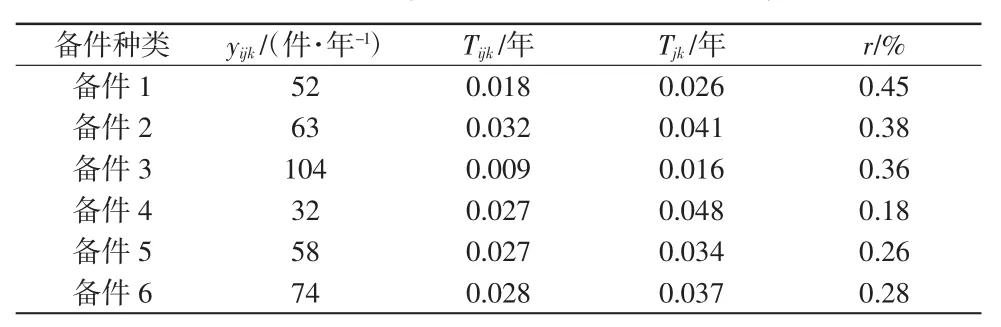
表1 区域维修中心1及其维修站的相关参数

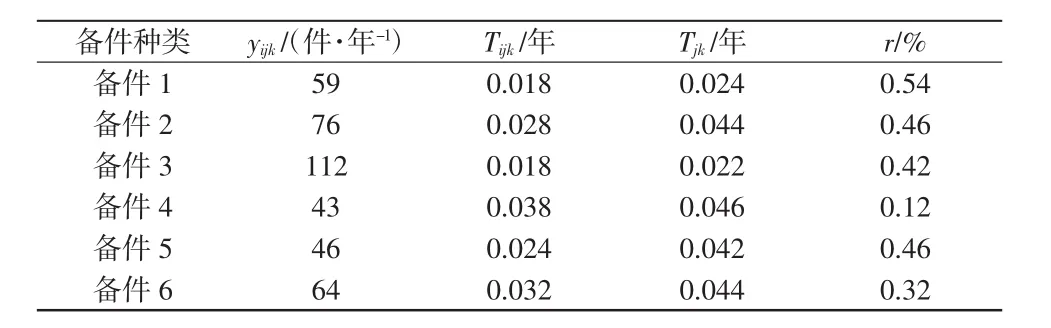
表2 区域维修中心2及其维修站的相关参数

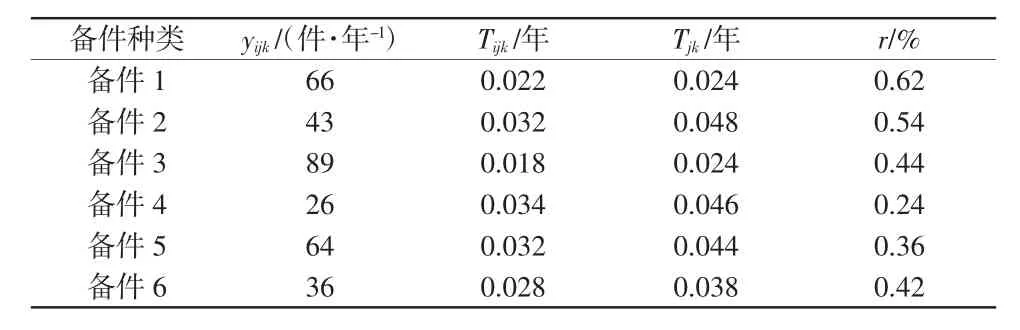
表3 区域维修中心3及其维修站的相关参数

4.2 算法分析

下面分别使用自适应遗传算法、多种群遗传算法、自适应多种群遗传算法来求解该案例中区域维修中心和维修站的最优备件库存量。

（1）自适应遗传算法：初始化种群大小为150，遗传代数为300，代沟为1。按照适应度函数计算种群个体的适应度，选择算子，算子选择100次，复制出100个个体。交叉算子控制参数为Pc1=0.85、Pc2= 0.33，变异算子控制参数为Pm1=0.042、Pm2=0.011。分别代入公式计算交叉变异概率，进行交叉变异操作。最后判断是否达到最大遗传代数300，如果没有，则转到选择复制，否则输出各变量值及最终的函数值。计算结果如下：

区域维修中心的库存量

二级维修站的库存量

最小的缺货期望E[B]=4.357 5。

计算结果如图2所示。

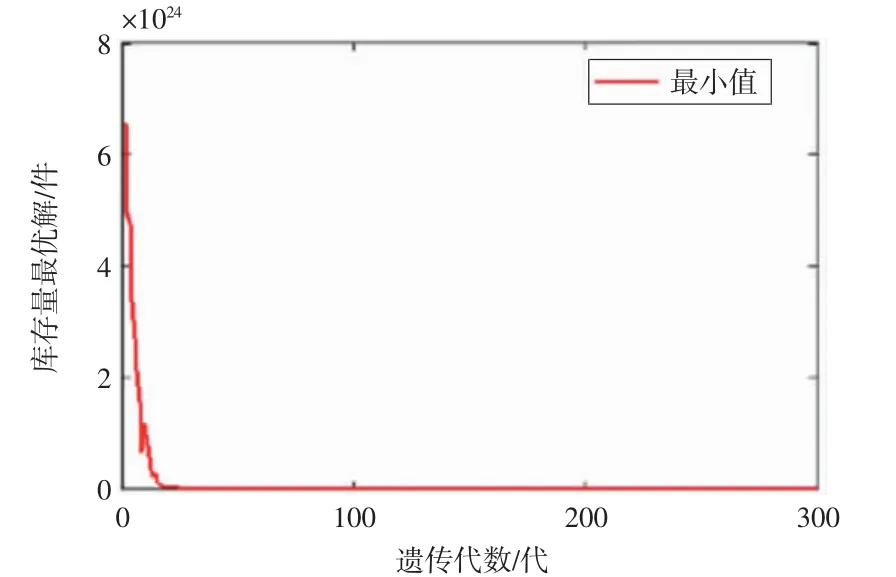
图2 自适应遗传算法结果进化图

（2）多种群遗传算法：初始化单个种群中个体数目为100，最优个体最少保持代数为20，代沟为0.9，并按要求随机产生交叉变异概率和10个初始种群，然后进行种群循环进化，最优个体满足最少保持代数条件时，终止循环。计算结果如下：

区域维修中心的库存量

维修站的库存量

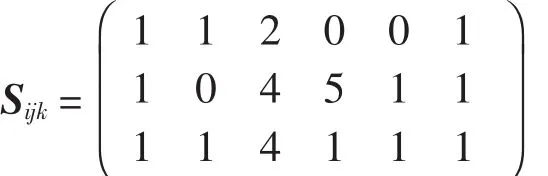
最小的缺货期望E[B]=4.223 5。

计算结果如图3所示。

（3）自适应多种群遗传算法：初始化种群数量为10，每个种群中有100个个体，代沟为1，最优个体最少保持代数为20，交叉算子控制参数为Pc1=0.85、Pc2=0.33，变异算子控制参数为Pm1=0.042、Pm2=0.001 1。计算得出的结果如下：

区域维修中心的库存量

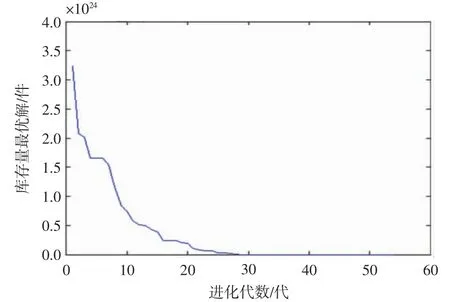
图3 多种群遗传算法结果进化图

维修站的库存量

最小缺货期望E[B]=0.249 94。

计算结果如图4所示。

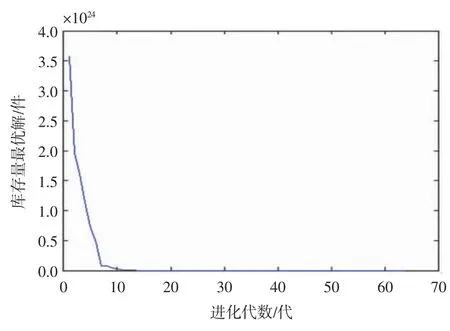
图4 自适应多种群遗传算法结果进化图

由图2～4可以看到，每个算法所求的目标函数值最后都是趋于稳定的，且随着进化代数的增加，目标函数值越来越小，符合预定的期望，这说明设计的算法在求解该模型时是有效的。另外，各算法所求解的目标函数值分别为4.357 5、4.223 5、0.249 94，对于所建的库存模型上，自适应多种群遗传算法更好地求解了该模型。再一次验证了自适应多种群遗传算法既有利于保留优良个体，又能保护群体的多样性，将自适应遗传算法和多种群遗传算法的优点集于一体，从而求得更优解。

此外，从计算出的维修站和区域维修中心的库存量来看，年需求量大的备件则相应库存量大，但由于需要考虑年预算，所以单价相对较高的备件库存量则会相应减少。由于维修站的年预算和年需求量相对区域维修中心较少，所以维修站中单价较贵的备件5和备件6的库存相对来说也要少一些。

4.3 结果分析

以自适应多种群遗传算法所解得的结果为例，对案例库存模型结果进行分析。

（1）首先，分析备件年平均需求量、备件单价与决策变量备件库存量之间的相关性。以维修站为例，根据已知的年平均需求量、单价，求出库存量，利用SPSS软件，分析其相关性，结果见表4。

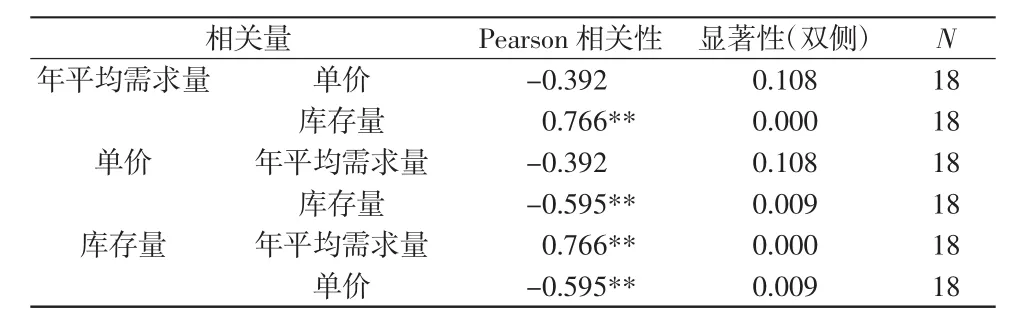
表4 库存量与单价、年平均需求量的相关性

由表4可以看出，备件的库存量与备件的年平均需求量、备件的单价均为显著相关。且备件库存量与年平均需求量成正显著相关，即当备件年平均需求量大时，备件的库存量也会在一定程度上增大。而备件的库存量与备件的单价则为负显著相关，即当备件单价相对较高时，备件的库存量在一定程度上相应减少。从而在一定的协调机制下，取得最优库存量。

（2）当区域维修中心备件的库存量发生一个单位的变化时，缺货期望会有什么变化，分别以单价相对较高的备件6和单价较低的备件3为例进行讨论。

①讨论S33（备件3在第3个区域维修中心的库存）的变化对缺货期望的影响，计算结果如图5所示。

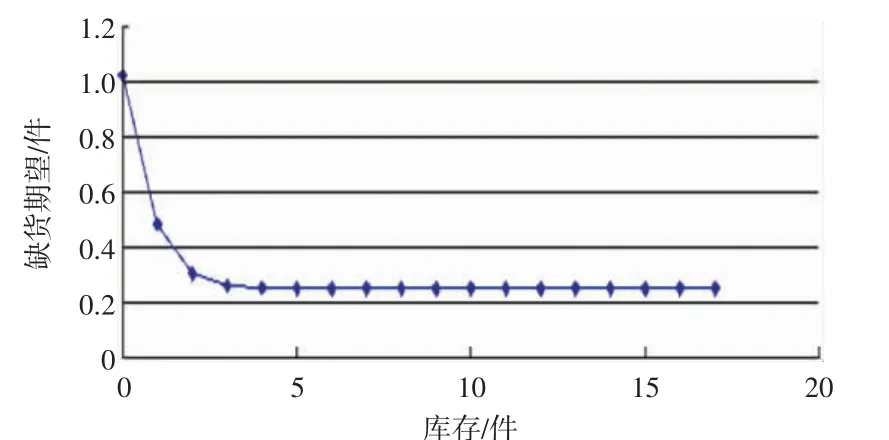
图5 S33与缺货期望的关系图

在库存数增加到7之前，缺货期望随着库存增大而减少，且变化幅度越来越小。模型求解时，求得的最优解是14，这是因为该备件单价相对较低，所以可以相对存储多一些。

②讨论S36（备件6在第3个区域维修中心的库存）的变化对缺货期望的影响，计算结果如图6所示。

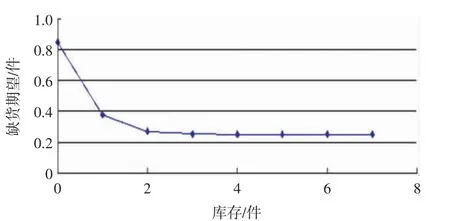
图6 S36与缺货期望的关系图

在库存数增加到5之前，缺货期望随着库存增大而减少，且变化幅度越来越小。模型求解时，求得的最优解是4，这是因为该备件的单价相对较高，存在年预算的限制。

（3）考虑区域维修中心的年预算费用变化，而其他参数值保持不变时对库存的影响。分别取区域维修中心年预算费用为5万、10万、15万、20万、25万、30万、35万、40万、45万、50万元，多次实验结果分别为

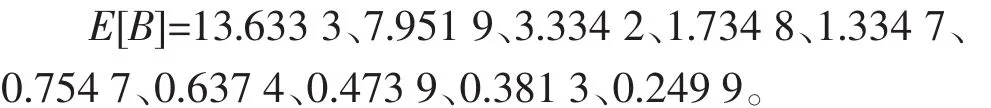
图7为区域维修中心年预算-缺货期望折线，横坐标表示年预算，纵坐标为相应缺货期望值。从图中可以看出，由于区域维修中心预算不够导致只能购买部分所需备件，尤其是单价相对较高的备件库存量低，致使最后缺货期望相应增加。

图7 区域维修中心年预算-缺货期望图

5 结论

本文考虑了医疗供应链中包括多个区域维修中心和多个维修站的二级库存，并建立了相应的模型。模型以区域维修中心和维修站的最小期望短缺数为目标函数，以区域维修中心和维修站的年预算为约束条件。然后分析模型并分别采用自适应遗传算法、多种群遗传算法、自适应多种群遗传算法求解模型。其中自适应多种群遗传算法结合了自适应遗传算法和多种群遗传算法的双重优点，所得结果优于另外2个算法，此算法能够较好地求解文中的库存模型，且该模型能有效地求解库存问题。通过建立医疗可修服务备件的库存模型，并设计优化算法，对优化医疗可修服务备件的库存水平、降低库存成本和呆滞资金、提高物流效益具有重要作用。

[1]Sherbrooke C C.METRIC：a multi-echelon technique for recoverable item control[J].Oper Res，1968，16（1）：122-141.

[2]Adams C M.Inventory optimization techniques,system vs.item level inventory analysis[C]//2004 Annual Symposium RAMS-Reliability and Maintainability.New York，America：IEEE Reliability Society Press，2004：55-60.

[3]Uthayakumar R，Priyan S.Pharmaceutical supply chain and inventory management strategies：optimization for a pharmaceutical company and a hospital[J].Operations Research for Health Care，2013，2（3）：52-64.

[4]Tancrez J S，Lange J C，Semal P.A location-inventory model for large three-levelsupplychains[J].TransportResE-Log，2012，48（2）：485-502.

[5]Jonrinaldi，Zhang D Z.An integrated production and inventory model for a whole manufacturing supply chain involving reverse logistics with finite horizon period[J].Omega，2013，41（3）：598-620.

[6]阚艳姣.汽车服务备件的多级库存建模与优化研究[D].合肥：合肥工业大学，2012.

[7]海冉冉.基于云自适应遗传算法的优化问题研究[D].吉林：东北电力大学，2013.

[8]贺步杰，夏文祥.装备备件最优库存建模——多级技术[M].2版.北京：电子工业出版社，2008：37-38.

（收稿：2015-09-13 修回：2015-10-12）

关于《医疗卫生装备》杂志征稿的严正声明

目前，社会上有非法团伙或中介冒充《医疗卫生装备》杂志编辑，利用虚假网站以杂志社编辑部或者杂志合作单位名义进行组稿，诱骗作者在线投稿、邮箱投稿，并以快速刊出论文、代写论文为诱饵骗取审稿费、版面费或中介费等，其手段隐蔽，具有极大的欺骗性。上当作者不仅会受到一定的经济损失，还有可能承担学术不端舆论风险。对此，《医疗卫生装备》编辑部提醒广大作者谨防钓鱼网站，以免上当受骗。

一、虚假网站稿件征集主要表现

声称（1）审稿周期短，承诺几天出结果；（2）刊出周期短，承诺当月见刊；（3）承诺包写论文，代发论文，保证发表；（4）要求作者将审稿费、版面费或变相的其他费用汇入个人账号或邮寄给个人；等等。

对此，我们郑重声明：《医疗卫生装备》杂志从没委托任何中介或个人进行约稿，从不收取审稿费，从不接收在线投稿；从不要求作者以设置密码方式邮寄版面费，从不要求作者将版面费汇到个人银行账户上。

二、识别假刊联系方式

由于假刊行骗者的欺骗手段、联系方式经常变换，所使用的网站也是经常改头换面，我们无法一一列举，希望广大作者提高警惕，加以识别，遇到可疑信息，请向本刊求证。在此，我们提供本刊编辑部正确的电话、投稿邮箱，请作者仔细核对。

本刊编辑部投稿及稿件查询电话：022-84656790/84659063/ 84656750/84656825

投稿邮箱：ylwszb@vip.sina.com，ynws@chinajournal.net.cn

本刊微信公众平台：医疗卫生装备；微信公众号：ylwszb。

行骗者的不法行为不仅严重损害《医疗卫生装备》杂志的声誉、造成作者的经济和精神损失，还严重地破坏了社会诚信。我们对以上假冒行骗行为予以谴责，并保留追究造假行骗者法律责任的权力。同时，我们也希望遭受经济损失的作者能够及时向当地公安机关举报或向本刊反映。

《医疗卫生装备》杂志社编辑部

Adaptive multiple-population genetic algorithm to optimize medical repairable spare parts inventory

LIU Shao-kai1,ZHANG Fang-yuan1,ZHU Hai-yu1,DUAN Lei1,WU Xiao-ling1,FANG Kun2
（1.Department of Biomedical Engineering,School of Basic Medical Sciences,Nanjing Medical University,Nanjing 210029,China;2.Logistics Center,Provincial Hospital Affiliated to Anhui Medical University,Hefei 230001,China）

Objective To research the inventory optimization of medical repairable spare parts and guide medical repairable spare parts inventory.Methods A medical repairable spare parts inventory model was established with mathematical modeling method and then solved with adaptive multiple-population genetic algorithm,which was based on the twoechelon model of the individual central warehouse for METRIC(multi-echelon technique for recoverable item control)repairable service spare parts.A two-echelon inventory optimization model was developed with hospital medical service spare part as the background,considerations including multiple service spare part suppliers,multi-area maintenance centers and multiple maintenance stations,annual budget as the constrained condition and minimized expected number of backorders as the objective.An adaptive multiple-population genetic algorithm was designed for the solution of the model above.Matlab was used to prove the correctness of the optimized model and the effectiveness of the algorithm.Results Adaptive multiple-population genetic algorithm integrated the advantages of adaptive genetic algorithm and multiple-population genetic algorithm,and solved the problems in the cost of medical service spare parts inventory.Conclusion Mathematical modeling and adaptive multiple-population genetic algorithm can optimize medical repairable spare parts inventory,and contribute to decreasing the cost of medical repairable spare parts inventory while increasing logistics efficiency. [Chinese Medical Equipment Journal，2015，36（12）：1-6]

medical repairable spare parts;two-echelon inventory;METRIC model;adaptive multiple-population genetic algorithm

R318；TP18

A

1003-8868（2015）12-0001-06

10.7687/J.ISSN1003-8868.2015.12.01

江苏省高等学校大学生创新创业训练计划2014年立项项目（201410312061X）

刘绍锴（1994—），男，主要从事医疗器械及物联网方面的研究工作，E-mail：ruofeng_02@163.com。

210029南京，南京医科大学基础医学院生物医学工程系（刘绍锴，张方圆，朱海煜，段 磊，吴小玲）；230001合肥，安徽医科大学附属省立医院物流中心（房 坤）

段 磊，E-mail：duanlei1979@163.com；吴小玲，E-mail：bmewxl @163.com