利用度量误差模型建立海南省松树和橡胶树质量与材积相容模型

甘世书

(国家林业局中南林业调查规划设计院，长沙 410014)

利用度量误差模型建立海南省松树和橡胶树质量与材积相容模型

甘世书

(国家林业局中南林业调查规划设计院，长沙 410014)

利用度量误差联立方程组模型方法，研建了海南省松树和橡胶树的一元与二元质量与材积相容模型，所建模型预估精度较高，达到了93%以上，模型具有良好的全面切合性能，可用于实际生产中。

度量误差模型；质量与材积相容模型；松树；橡胶树；海南省

松树和橡胶树是海南省主要用材树种，也是两大重要的工业原料树种，主要生产松脂和天然橡胶，每年都面临着大量的更新采伐。而在实际采伐过程中，经常需要估计立木的质量。为了方便于生产，快捷准确地利用单株立木材积测算出树干(去皮)质量，编制树干(去皮)质量与树干去皮材积的关系模型是切实可行的办法之一，也具有十分重要的现实意义。

由于在质量与材积转换模型中，以材积作为自变量，而材积主要通过材积模型获得，因此材积自变量不可避免的带有误差，用无误差变量采用普通回归估计方法建模已不再适宜。针对此问题，本文采用了度量误差联立方程组模型方法研究建立了质量与材积相容性模型，以期为实际生产提供可靠的计量工具。

1 建模样本收集与处理

1.1 建模样本收集方法

研建通用型模型，为了保证其适用性，将样本采集范围尽可能覆盖海南省各个地区，同时尽可能扩大样本变量(胸径、树高)的覆盖范围，以真实反映变量间相关规律的完整性、真实性和稳定性[1]。因此将松树和橡胶树的取样范围按胸径分为6，10，16，22，28和32 cm以上共6个取样点位。在每点位取样时要求尽量按树高的实际变化范围分低、中、高(以高径比控制)选取样木，伐倒后在0/10，0.5/10，1/10，2/10，…，9/10树高处实测带皮和去皮直径，同时采集各样木鲜质量样品。

为了减少外业调查难度，将树干3/10树高处(去皮)的密度作为整个树干(去皮)平均密度。调查样本的长度统一为100 cm，位置以3/10树高分接处为中点，上下各取50 cm。保证取样长度误差在±1 cm范围内。用油锯截取称样本，截取时使锯路尽量与树干垂直。锯完后，分别测量上下两头的去皮直径，同时复测样本的长度，并按最长和最短的位置测2次，取平均值。

样本质量统一用电子称称量。在取样后48 h， 96 h和144 h后再分别测定各样本的质量，起算时间以标记的时间为准，时间误差应控制在±1 h范围内，原则上不能超过±2 h。松树和橡胶树具体的建模样本资料按径级分布情况详见表1。

表1 建模样本资料按径级分布情况径阶/cm建模样本/株松树橡胶树62727102627162727222627282627≥322326合计155161

1.2 建模样本处理

首先根据样木样段计算其去皮材积，进而计算样木密度，在根据整样木去皮材积计算整样木质量。

具体计算各样木样段去皮材积公式如下[2]：

式中：V样品为样木样段去皮材积(m3)，D大为大头去皮直径(cm)，D小为小头去皮直径(cm)，L为长度(m)。

计算整样木去皮材积公式如下：

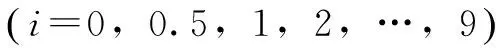
分别将松树和橡胶树按建模样本与检验样本作材积与质量对应关系散点图，分析表明，样本资料中无异常样木，所采集的样木均用于建模和检验。

2 研究方法

2.1 度量误差联立方程组模型

通常的回归模型，是假定自变量的观测值不含误差，而因变量的观测值含有误差。而实际中两者都可能存在误差，如抽样误差、测量误差等，这些各种来源的误差统称为度量误差。当自变量和因变量的观测值中都含有度量误差时，通常的回归模型估计方法就不再适用，而必需采用度量误差模型方法，非线性度量误差联立方程组方法一般明显优于最小二乘法[3]。

根据数据分析表明，一元质量模型和二元质量模型差异不大，因此在建立联立方程组模型时质量模型统一采用一元模型。

一元模型结构如下：

V=a0×Da1

W平均=b0×Db1×V

二元模型结构如下：

V=a0×Da1×Ha2

W平均=b0×Db1×V

W平均取样木在伐倒后48 h，96 h和144 h后三次测量的去皮湿质量的平均值，V为去皮材积，D为胸径，H为树高，ai和bi为模型参数。

2.2 异方差处理

由于材积和质量数据普遍存在着异方差性，在利用非线性回归方法进行拟合时还要采取措施消除异方差的影响[4-5]。常用的方法有采用对数回归或者加权回归，均采用非线性加权回归的方法。关于权函数的选择，根据独立拟合方程的方差建立与自变量之间的回归方程。

2.3 模型评价

用6个指标来对模型进行评价和检验。确定系数R2，估计值的标准差SEE，总相对误差TRE，平均系统误差MSE，预估精度P和平均百分标准误差MPSE，计算公式如下：

3 结果分析

3.1 模型拟合结果

采用非线性加权回归方法对模型参数进行估值，具体模型拟合结果见表2。

从表2中统计可知，无论一元模型还是二元模型，模型均具有较高的确定系数、较小的剩余标准差、较高的预估精度，模型的TRE和MSE都在±3%以内，模型拟合结果良好。当模型从一元提升到二元，松树的立木去皮材积模型和质量模型的P和R2均有大幅度地提高，SEE也有大幅地的下降，而橡胶树模型从一元提升到二元，模型P和R2两个指标提高的幅度不大，只有SEE指标有明显下降。以上分析说明用一元、二元模型来估计均是合适的。在实际工作中，如果要得到更高精度的预估值，则优先采用二元模型。

表2 一元和二元相容性模型拟合结果树种类型模型abcR2SEEP/%MPSE/%TRE/%MSE/%一元材积6.8361E-52.6076470.89340.0935893.9120.580.190.03质量798.3739430.062532 0.888296.2021893.6420.990.190.06松树二元材积3.5263E-51.891691.0543040.98010.0405297.368.972.080.23质量754.2160620.082716 0.977443.3975997.1311.391.000.50一元材积1.48877E-42.413606 0.95460.0616196.5616.95-0.64-1.04质量796.3552810.039481 0.947459.3680296.3718.67-0.21-4.48橡胶二元材积5.6588E-51.9295430.8665950.96800.0506697.1710.582.46-0.06质量652.165980.104626 0.955954.5360396.6613.591.28-2.11

3.2 模型检验

3.2.1 模型残差随机性检验

根据松树和橡胶树材积残差和质量残差的分布图来看，所建立的一元和二元相容模型残差基本服从随机分布，不存在明显的系统偏差，模型具有良好的全面切合性能。由于篇幅限制，在此只列出了松树残差分布图，见图1、图2。

3.2.2 分段检验

作为通用性预估模型，仅采用上述统计指标进行整体评价尚不足以充分辨识所建模型的效果，还需要采用TRE和MSE2个统计指进行分段检验。具体分段检验的结果见表3。

从表3中统计指标可知，松树一元相容性模型在10 cm径阶下，质量和材积模型的TRE、MSE指标在10%以上；在其它各径阶下，质量和材积模型的TRE、MSE指标基本上在±5%以内。松树二元相容性模型在各径阶下，质量和材积模型的TRE、MSE指标基本上在±5%以内；且二元相容性模型要明显优于一元相容性模型，这主要原因在于，模型从一元提升到二元，很大程度上提高了材积模型的预估精度，因此也就提高质量模型在各径阶下的适用性。

图1 松树一元质量与材积相容模型残差随胸径分布图

图2 松树二元质量与材积相容模型残差随胸径分布图

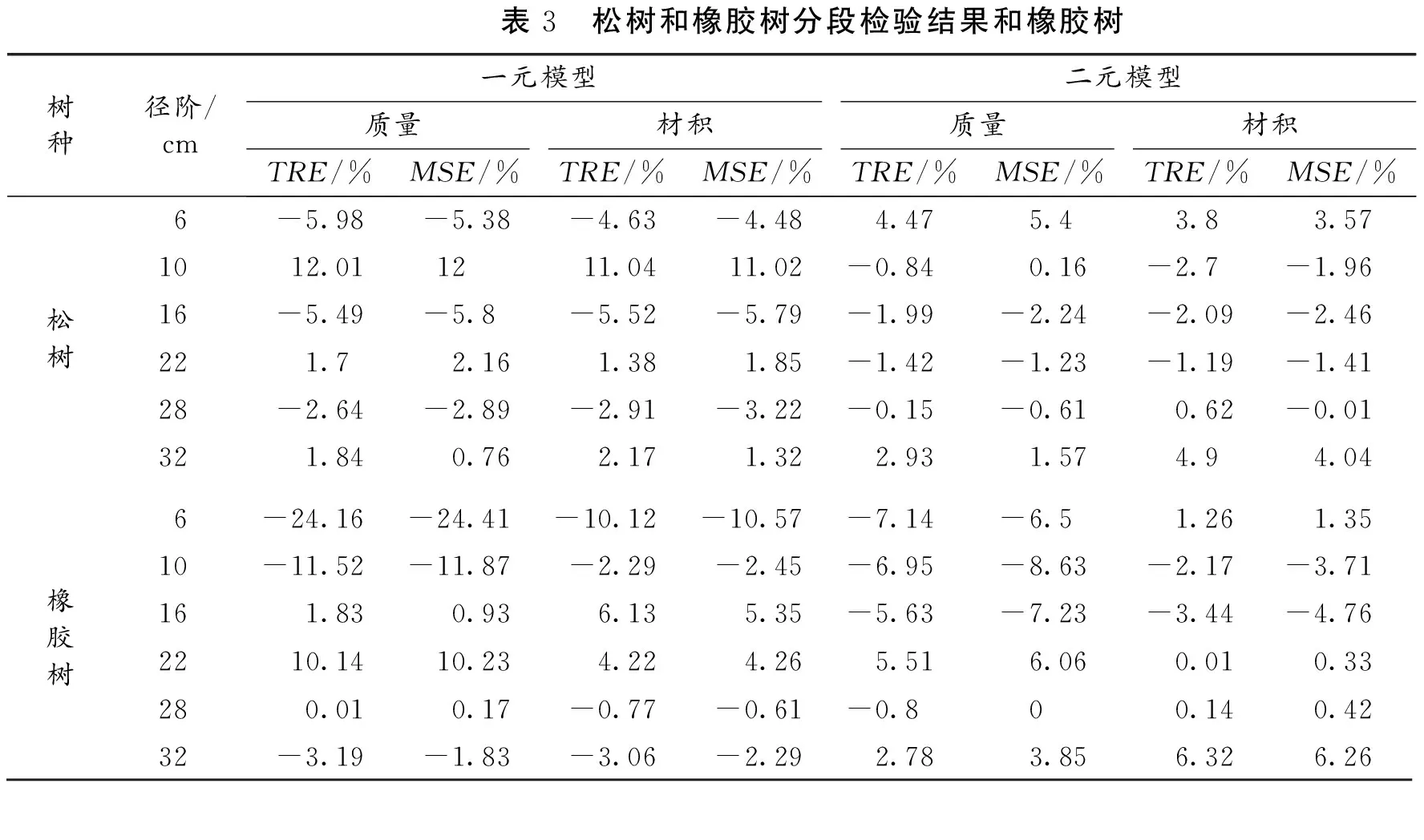
表3 松树和橡胶树分段检验结果和橡胶树树种径阶/cm一元模型二元模型质量材积质量材积TRE/%MSE/%TRE/%MSE/%TRE/%MSE/%TRE/%MSE/%6-5.98-5.38-4.63-4.484.475.43.83.571012.011211.0411.02-0.840.16-2.7-1.9616-5.49-5.8-5.52-5.79-1.99-2.24-2.09-2.46松树221.72.161.381.85-1.42-1.23-1.19-1.4128-2.64-2.89-2.91-3.22-0.15-0.610.62-0.01321.840.762.171.322.931.574.94.046-24.16-24.41-10.12-10.57-7.14-6.51.261.3510-11.52-11.87-2.29-2.45-6.95-8.63-2.17-3.71161.830.936.135.35-5.63-7.23-3.44-4.76橡胶树2210.1410.234.224.265.516.060.010.33280.010.17-0.77-0.61-0.800.140.4232-3.19-1.83-3.06-2.292.783.856.326.26

从表3中统计指标可知，橡胶树一元质量与材积相容模型，在6 cm径阶、10 cm和22 cm径阶下，存在着一定的偏差，在其它各径阶下模型的TRE和MSE指标均在±4%以内，这主要原因在于，橡胶树分叉枝条较多，单靠胸径而未考虑树高的影响很难准确反映材积的变化规律。因此，橡胶树二元质量与材积相容模型要明显好于一元相容模型，在各径阶下，二元相容模型的TRE和MSE基本上在±7%以内，且无明显系统偏差。

4 结论与建议

本文利用度量误差联立方程组模型方法，为海南省松树、橡胶树两个树种分别建立了一元和二元质量与材积相容模型，经模型检验分析表明：

1) 度量误差联立方程组模型能有效解决材积方程和质量方程之间不相容的问题，并可同时建立立木材积方程、质量方程及其转换函数，确保了相互之间估计结果的协调一致性和参数稳健性。

2) 所建立的一元和二元相容性模型拟合效果均很好，当模型从一元提升到二元时，材积模型的精度有大幅度地提高，从而导致质量模型的全面切合性能得到显著提高。尽管一元模型在各别径下，存在着一定的偏差，但对总体预估是无偏的。在实际生产中应注意模型的适宜范围，一元模型主要应用于较大总体范围内的估计，对于小区域范围或者单木的质量估计，则应考虑使用二元模型。

[1] 骆期邦，曾伟生，贺东北. 林业数表模型——理论、方法与实践[M]. 湖南: 湖南科学技术出版社，2001.

[2] 孟宪宇. 测树学[M]. 北京: 中国林业出版社，2006.

[3] 唐守正, 郎奎建, 李海奎. 统计和生物数学模型计算ForStat教程[M]. 北京:科学出版社，2009.

[4] 曾伟生, 骆期邦,贺东北. 论加权回归与建模[J]. 林业科学, 1999, 35(5 ): 5- 11.

[5] 曾伟生, 唐守正.立木生物量模型的优度评价和精度分析[J].林业科学, 2011, 47( 11): 106-113.

UsingMeasurementErrorModelingMethodtoEstablishCompatibleWeightandVolumeModelforPineandRubberinHainan

GAN Shishu

(Central South Forest Inventory and Planning Institute of State Forestry Administration, Changsha 410014, Hunan, China)

In this paper, we established one-way and two-way compatible weight and volume models for pine and rubber in Hainan province, using measurement error modeling method. The precision of these models were significantly high, more than 93%, these models have good comprehensive appropriateness and can be used in practical production.

measurement error model；compatible weight and volume model；pine；rubber；Hainan

2015-06-12

甘世书(1963-)，男，湖南湘阴人，高级工程师，主要从事森林资源监测等工作。

S 757.2

A

1003-6075(2015)04-0045-04

10.16166/j.cnki.cn43-1095.2015.04.012