带模糊数的运输问题研究

孙方远，朱海定

（上海大学 管理学院，上海200444）

SUN Fang-yuan, ZHU Hai-ding

(School of Management, Shanghai University, Shanghai 200444, China)

0 引 言

一般来讲，运输问题可分为单目标运输问题和多目标运输问题。运输问题最早是由Hitchcock[1]于1941 年提出，它指的是货物从生产商到销售商的分配问题。这样的运输问题也称之为经典的运输问题，其目标只有一个，且约束均为等式。但在实际运输问题中，人们考虑的因素往往较多，包括在使得费用最小的情况下，同时考虑时间限制、质量等，要达到的目标不止一个，也就产生了多目标运输问题（MOTP）。然而，在现实世界中，目标函数的系数常常不能确定，供应量和需求量也常常如此，因而问题的目标和约束就可能是模糊的，这也就使得多目标模糊运输问题（MOFTP） 应运而生。本文为了使大家对运输问题能够有更加深入系统的认识，对单目标运输问题和多目标运输问题分别做介绍，再各自深入到带模糊数的单目标运输问题和带模糊数的多目标运输问题，给出模型、算法和算例。

1 带模糊数的单目标运输问题

1.1 经典运输问题

经典运输问题就是指把某种物资从若干个供给地运往若干个需求地，各供给地的供给量、各需求地的需求量已知，各供给地与需求地之间的交通是否可达也已知，据此解决如何安排运输使总运费最少的问题。

经典的运输问题描述如下：供应点以Si（i=1,2,…,m）表示，有m个；需求点以Dj（j=1,2,…,n）表示，有n个。第i个供应点的可供量以ai（i=1,2,…,m）表示，第j个需求点的需求量以bj（j=1,2,…,n）表示。从供应点Si向需求点Dj运送一单位物品的运输成本为cij。求使得总运输成本最小的调运方案。xij是决策变量，表示即将从供应点Si向需求点Dj运送的商品数量，此传统运输问题的数学模型可表示为：

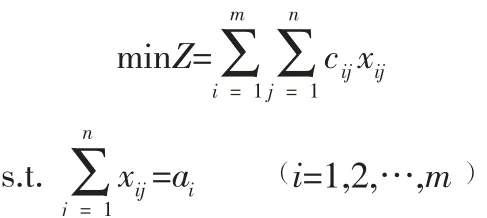
1.2 带模糊数的单目标运输问题

1.2.1 带模糊数的单目标运输问题模型。为了使经典的运输问题能更加切实地反应模糊的世界，对以上模型中的参数第i个供应点的可供量ai（i=1,2,…,m）和第j个需求点的需求量为bj（j=1,2,…,n）分别取三角模糊数和得到带模糊数的单目标运输问题的模型如下：

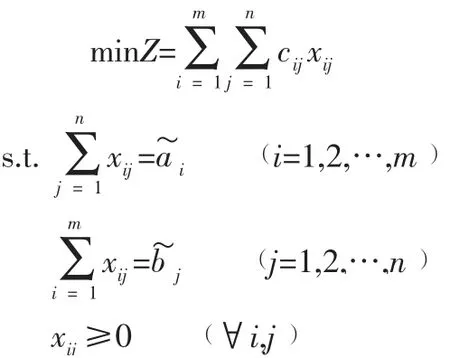
1.2.2 带模糊数的单目标运输问题的算例应用。假如已知运输单价、供给量及需求量如表1，试求运费最小的调运方案。

表1 运输表

根据此表可得到如下模型：

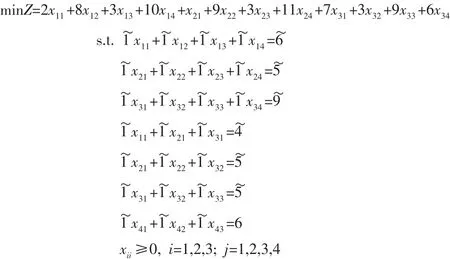
根据高淑萍在其文章中用的三角模糊数排序准则[2]，可将该问题化为如下线性规划问题：

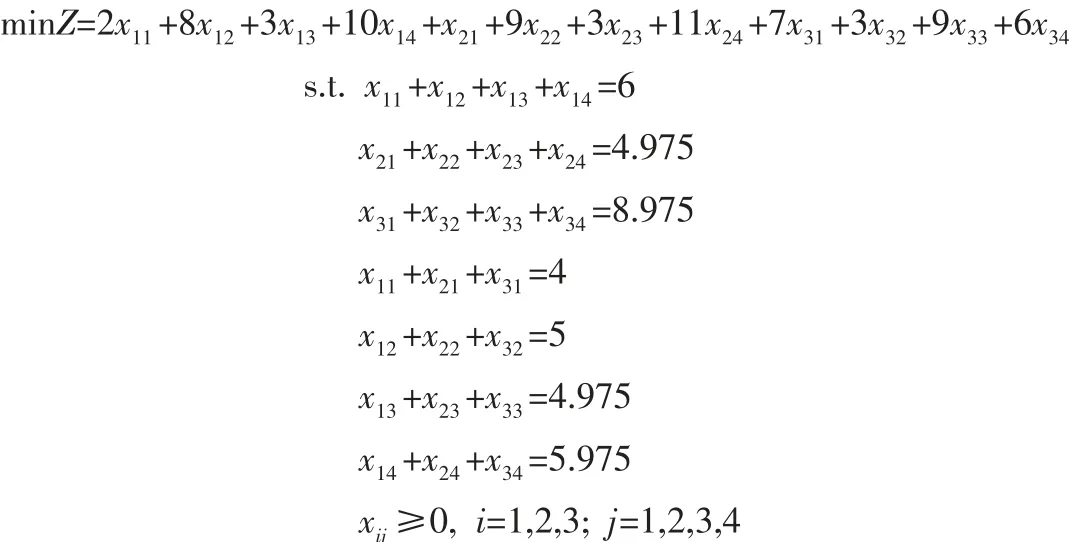
用Lingo 软件解得：

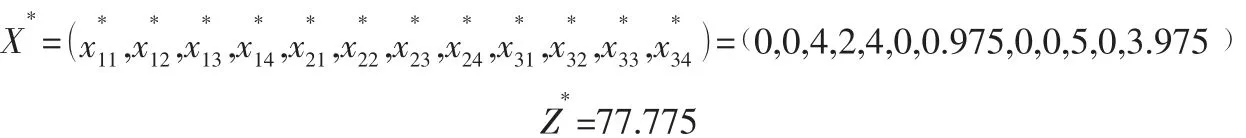
2 带模糊数的多目标运输问题

2.1 多目标运输问题

单目标运输问题是考虑使运输总成本最小这一个目标的运输问题，然而在现实中要考虑的因素往往不止成本这一项。现实生活中大量的运输问题要综合考虑多个目标的优化问题。比如，在一个物流配送系统中，除了对总运输费用有要求外，还要求商品运输的可靠性、平均交货时间甚至客户最满意等也要有所要求，这些不同的要求也就形成了本物流配送需要达到的不同目标。

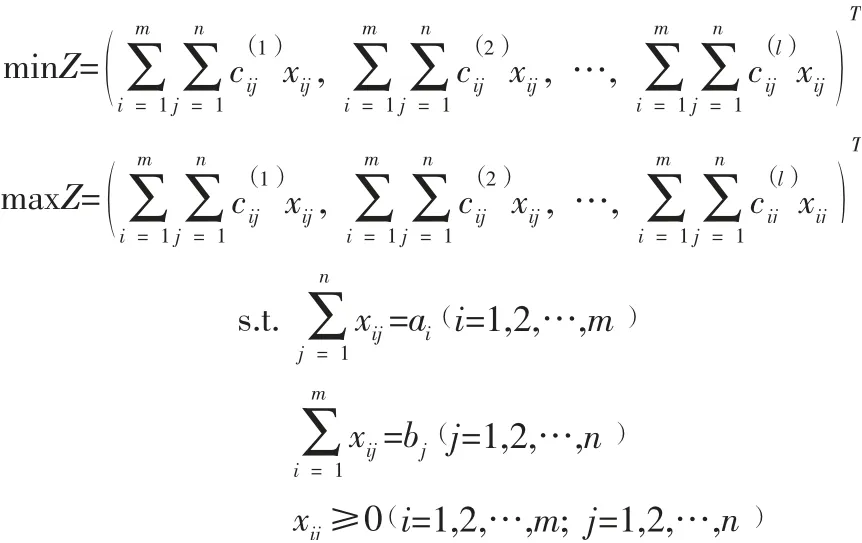
其中，ai≥0 表示第i个生产地的产量；bj≥0 表示第j个销售地的销量；目标中可以表示总运费、总运输时间、总运输能耗或运输对环境所造成的污染等；在最大化目标中，可以表示总质量、满意度、可靠性等。

对于多目标运输问题的求解，不同学者运用了不同的解法。熊国强等人提出一种求解多目标运输问题的目标协调优化方法[3]，白国仲给出了求解多目标运输问题的表上作业法[4]，罗霞，廖勇和李录书用模糊规划法求解多目标运输问题[5-6]。对这三种求解多目标运输问题的方法进行对比分析，熊国强等人提出的目标协调优化方法，易于掌握，易于操作，是相对最优的。

2.2 带模糊数的多目标运输问题

2.2.1 带模糊数的多目标运输问题的模型。考虑在实际的运输问题决策中，相关参数，如销地的货物需求量、产地的货物生产量及运输货物的单位运价的确定往往带有随意性或经验性，因而不那么精确。故会考虑把这些参数设成模糊参数，从而得含模糊参数的多目标运输问题的模型如下：

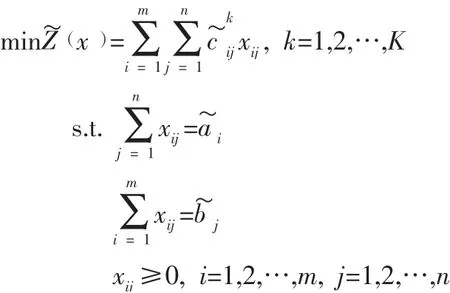
对含有模糊参数的多目标运输问题的求解，不同的学者也提出不同的解法。宋业新等人运用一种对模糊数排序的方法，将模糊多目标运输问题转化为单目标运输问题进行求解[7]。罗霞，廖勇利用三角模糊数的大小关系和模糊数的数学特征分别对目标函数和约束中的模糊参数去模糊化，从而模糊多目标运输模型变成普通的多目标运输模型，再进行求解[5]。

2.2.2 带模糊数的多目标运输问题的算例应用。求解如下运输问题：供给地A 和供给地B 为运输物资提供方，需求地有3 个a、b 和c，考虑运输成本、供应量和需求量的模糊性，用三角模糊数表示之，得问题模型如下：

用罗霞[5]的求解方法对其进行求解：

第一步，将目标函数和约束条件进行分家，计算不同目标在约束条件下的最优解。目标函数被分解成如下4 个：

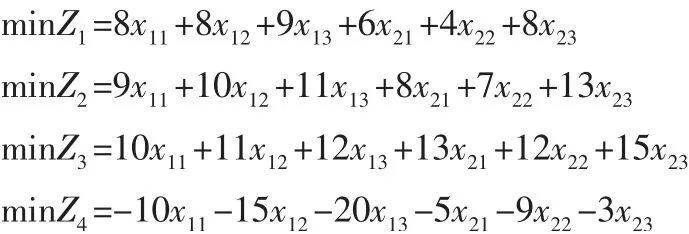
约束为：

得到的解如表2：

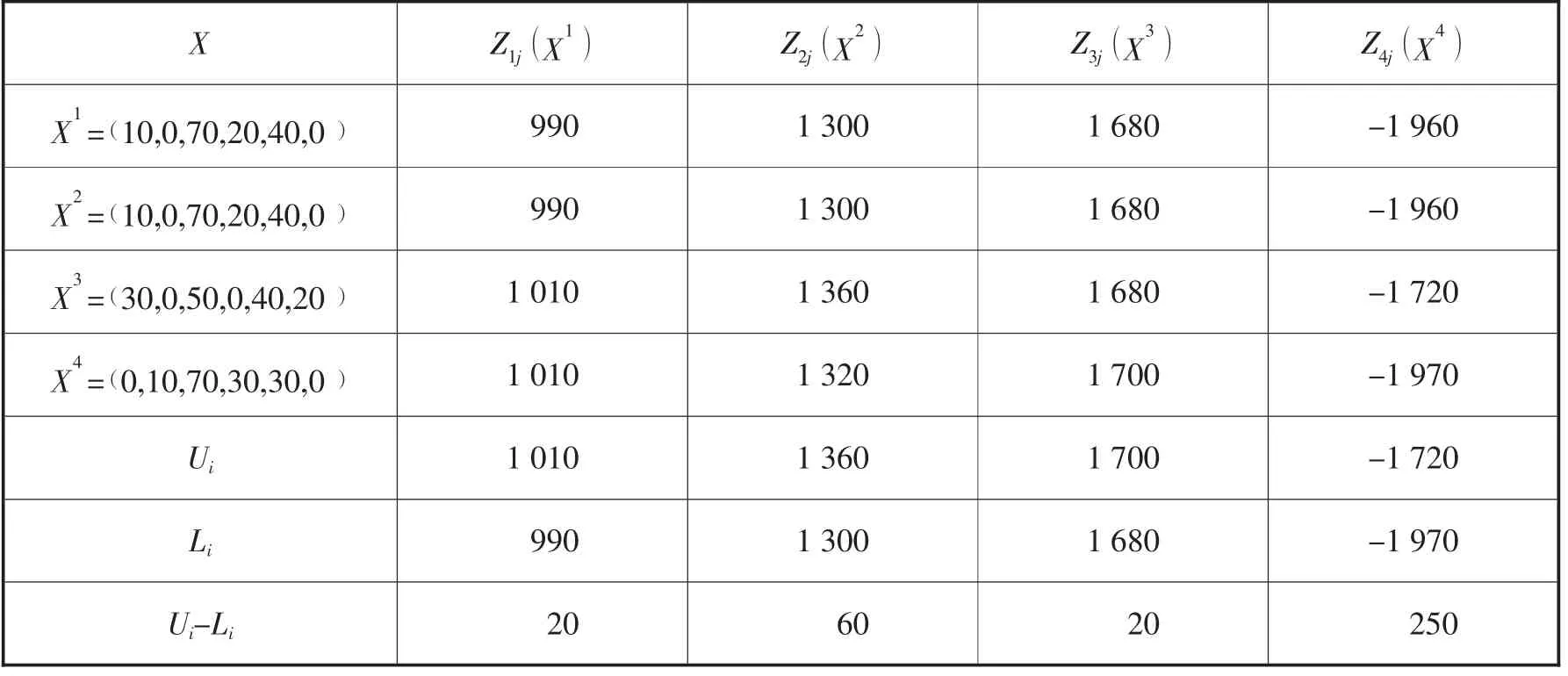
表2

第二步，根据以上结果可得如下各个目标的隶属度函数：

第三步，根据表2 的计算结果，建立转换后的模型如下，其中以λ 最小为目标，并将目标函数转为实数下的约束条件，把模糊约束也转为实数下的约束条件，转化后的模型如下：

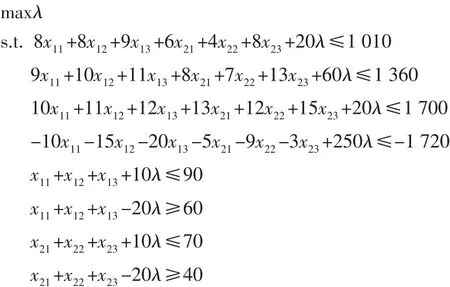
最后，利用Lingo 软件求解第三步中的模型，解得X*= （0,19.37,62.59,28.32,17.45,5.14），各目标值依次为999.11、1 297.72、1 618.81 和-1 856.42。并可求得各个目标的满意度（μ1（z1）～μ4（z4））分别为0.5445、1、1 和0.5457。

3 小 结

本文对运输问题的研究中加入了模糊参数。从经典的运输问题的介绍到带模糊数的单目标运输问题的介绍，再从一般的多目标运输问题的介绍到带模糊数的多目标运输问题的介绍，对运输问题的诠释层层深入。并且在给出这4 类模型的同时还附带了算例及其求解，更进一步展示了运输问题的运用情况。对4 类运输问题的算法进行总结可知，最终均能化为线性规划问题，利用Lingo 软件进行求解。因此，本文相对系统的总结了运输问题的各种情况，在研究运输问题时，有一定的参考性。

[1] Hitchcock F.L.. The distribution of a product from several sources to numerous localities[J]. Journal of Mathematical Physics,1941,20:224-230.

[2] 高淑萍. 运输问题的模糊优化算法和理论研究[D]. 西安：西安电子科技大学（博士学位论文），2003.

[3] 熊国强，潘泉，张洪才. 求解多目标运输问题的一种目标协调优化方法[J]. 系统管理学报，2007,16(5):528-536.

[4] 白国仲. 求解多目标运输问题的表上作业法[J]. 信阳师范学院学报，2007,20(4):403-408.

[5] 罗霞，廖勇. 多目标模糊运输问题的建模与求解[J]. 西华大学学报（自然科学版），2010,29(4):43-47.

[6] 李录书. 多目标运输问题的fuzzy 线性规划解法[J]. 运筹与管理，1994,3(1):11-16.

[7] 宋业新，陈锦云，吴晓平. 具有模糊信息的多目标运输问题求解[J]. 模糊系统与数学，2001,15(3):86-89.