高速动目标多频段融合一维超分辨成像算法研究

李　威，梁福来，张　毅，吕　昊，罗二平

高速动目标多频段融合一维超分辨成像算法研究

李威，梁福来，张毅，吕昊，罗二平

目的：提出一种新的融合成像算法，解决现有目标模型及算法在宽带条件下对高速动目标频响建模不精确的问题，提高成像分辨率。方法：将衍射几何理论（geometrical theory of diffraction，GTD）模型与目标运动相结合，推导出宽带雷达动目标回波频谱模型，分析动目标多频段雷达回波间的非相干量，在频域对每部雷达的回波谱进行匹配滤波和速度补偿，基于实包络对齐估计线性相位项，利用旋转矢量不变技术（estimating signal parameters viarotational invariance techniques，ESPRIT）算法特性直接估计散射中心的绕射系数和位置，最后估计散射强度。结果：通过仿真实验，新的图像融合算法与传统算法相比，在线性相位项的补偿和强散射中心个数估计的精度上均有所提升，成像效果显著改善，且新算法大大地精简了计算过程。结论：新的融合成像算法可显著提高快速运动目标距离像的分辨率。

高分辨距离像；线性频率调制；速度补偿；相干融合

0　引言

近年来，目标的一维高分辨距离像（high resolution range profile，HRRP）在目标成像、目标识别以及导弹防御等民用和军用领域都有广泛应用，相关研究中一个重要的研究问题就是如何获得高分辨距离的成像。理论上可通过增加发射带宽提高距离分辨率，但这对雷达硬件提出了更高的要求，将会大幅增加成本。而多频段融合成像技术可将独立工作于不同频段、不同带宽的多雷达回波数据融合到一起以达到增大带宽的目的。

多频段融合成像技术最早见于林肯实验室Cuomo的研究中[1]，国防科技大学自动目标识别（auto targets recognition，ATR）重点实验室的王成等人对稀疏子带的多频段融合成像技术做了进一步的研究[2-5]。这些研究均未考虑目标运行速度对融合成像的影响。在实际中，许多被观测目标往往具有较高的空间运行速度，根据距离多普勒耦合效应原理，目标的高速运动将对测量系统的线性调频信号造成影响，最终对一维距离成像产生展宽并发生时移。在做多频段融合处理时如果不对目标运动进行有效补偿，将导致融合距离像的质量下降。

本文首先推导了宽带动目标回波信号模型，之后在频域分别对各子频段数据进行预处理（包括脉冲压缩和速度补偿等）；分析了造成动目标多频段回波之间不相干的因素，得出了动目标多频段之间的非相干量主要由线性相位项和固定相位项组成。通过对比可以发现，动目标与静目标二者在多频段回波信号中的非相干量是相同的，故可以参考现有的相干方法来处理动目标问题。

现有经典的相干方法主要是通过外推各子频段频谱求得重叠频带，然后基于最小二乘准则估计非相干量[1]。傅耀文等人提出可以通过将外推各子频段频谱所求得的重叠频带转换成距离像并求解出距离像的线性相位项，通过构造相干函数来估计固定相位项[6]。以上2种方法从不同的角度解决了相干问题，取得了较好的估计效果。但2种方法都涉及外推各子频段频谱，外推过程不可避免地会降低估计精度，且相关工作的计算量比较大，耗时较长。国防科技大学ATR实验室的王成提出可以通过建立相干成像模型，利用现有谱估计方法对非相干量参数进行估计[5]。该方法虽然免去了频谱外推的步骤，一定程度上解决了降低精度的问题，但是估计中要做多次旋转矢量不变技术（estimating signal parametersvia rotational invariance techniques，ESPRIT）运算，计算量大，效率较低。

本文提出了一种新的相干融合方法，该方法不需作频谱外推，简单有效。该方法首先利用实包络对齐求解线性非相干量，其优点是对信噪比要求较低、计算量小且估计精度较高；通过特殊的数据重排，构造具有旋转不变性的自相关矩阵，可直接利用已有的ESPRIT算法进行融合成像。通过分析发现，ESPRIT成像算法不受固定相位项的影响，利用补偿过线性相位项的回波数据就可以准确估计极点，基于子频带散射强度的相位差异估计固定相位项，最后通过最小二乘估计散射中心强度。计算机仿真实验验证了本文所提方法的有效性。

1　动目标宽带雷达回波建模

运动点目标宽带雷达回波模型及速度补偿的方法已经在文献[7]中给出。但在宽带甚至超宽带条件下，散射强度随频率变化，传统的点散射模型已不能适应需要，而且散射类型对于判别目标类型也很有好处。所以本文将衍射几何理论（geometrical theory of diffraction，GTD）模型作为目标的频率响应推导动目标宽带回波模型[8-9]。

设某部雷达发射的线性调频（linear frequency modulation，LFM）信号为

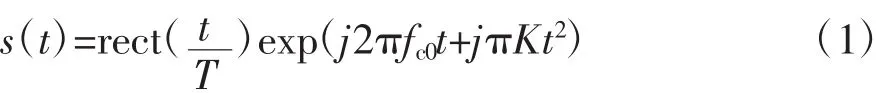
其中

式（1）中，fc0为载频，K为调频斜率，T为脉宽。假设发射信号的频谱为s（f），若目标由静止散射点构成，则回波频谱为

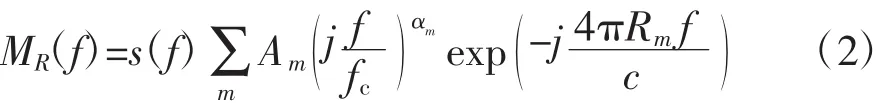
式（2）中，Am为第m个散射中心的散射强度，fc为合成全频带的中心频率，αm为第m个散射中心的频率依从系数，Rm为第m个散射中心与雷达间的相对距离，c为光速。若令

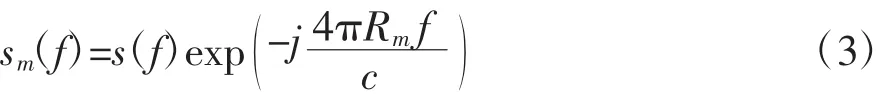
式（2）可以表示为

将式（3）变换到时域得

对动目标来说，Rm是随时间变化的量[7]。

式（6）中，vm为第m个散射中心的速度。式（5）可以表示成下式：

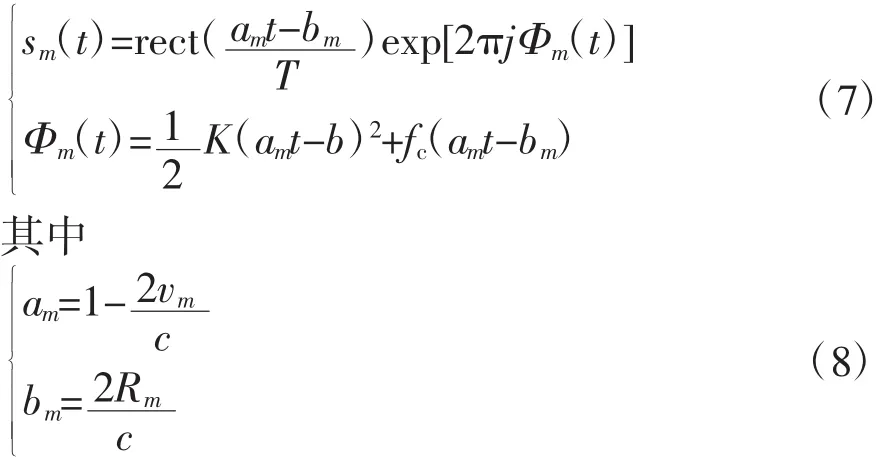
式（4）可写成如下形式：

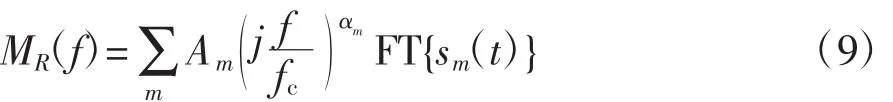
式（9）中，FT{·}表示作傅里叶变换。显然sm（t）仍然是LFM信号，对式（9）进一步推导得

式（10）即为发射信号为LFM信号、目标频响为GTD模型的单频段动目标回波模型。

2　多频段动目标回波预处理

对接收到的回波信号进行匹配滤波：

式（11）中，符号“*”指取共轭。

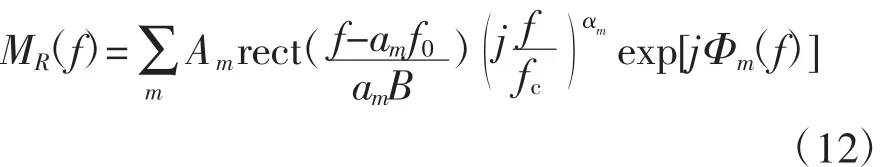
其中

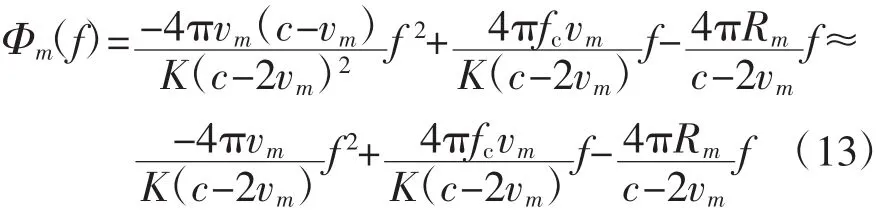
式（13）中的第1项为谱线展宽项，会造成分辨率的降低；第2项会使距离像平移，但不影响单个频段成像；第3项是包含散射中心的位置信息，要予以剥离。考虑到多频融合成像技术要求尽量减少频段间的非相干量，所以要对第1项和第3项进行补偿。因为各频段的载频和调频斜率不同，因此在具体计算中，需要区别对待，分别单独补偿。假设目标径向速度的估计值为vˆ，速度补偿后的回波相位表达式为

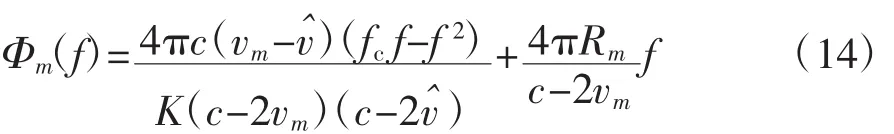
预处理的流程如图1所示，高、低子频带的回波数据经过解调和滤波进行补偿，得到的回波数据量比较大，可在频域作降采样处理，降低数据量，便于后续处理。

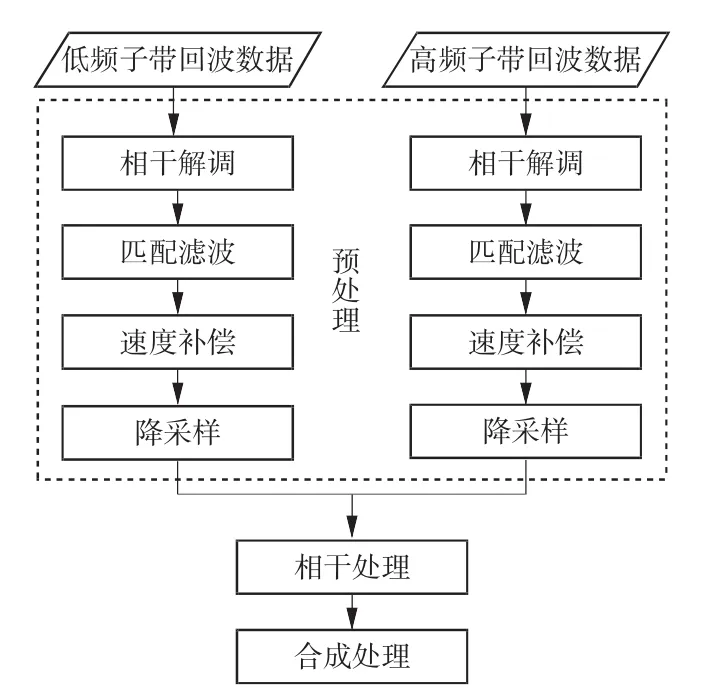
图1　多频段动目标回波预处理流程图

3　动目标多频段雷达回波非相干量分析

麻省理工学院（Massachusetts Institute of Technology，MIT）林肯实验室的Cuomo通过雷达信号的相位误差分析，认为对低速目标而言，造成多部雷达非相干的原因主要有信号发射时间不同步、雷达距离位置不同和初始相位不同3个方面[1]。而对于高速运动目标，速度补偿也会一定程度上造成雷达间回波信号的不相干。

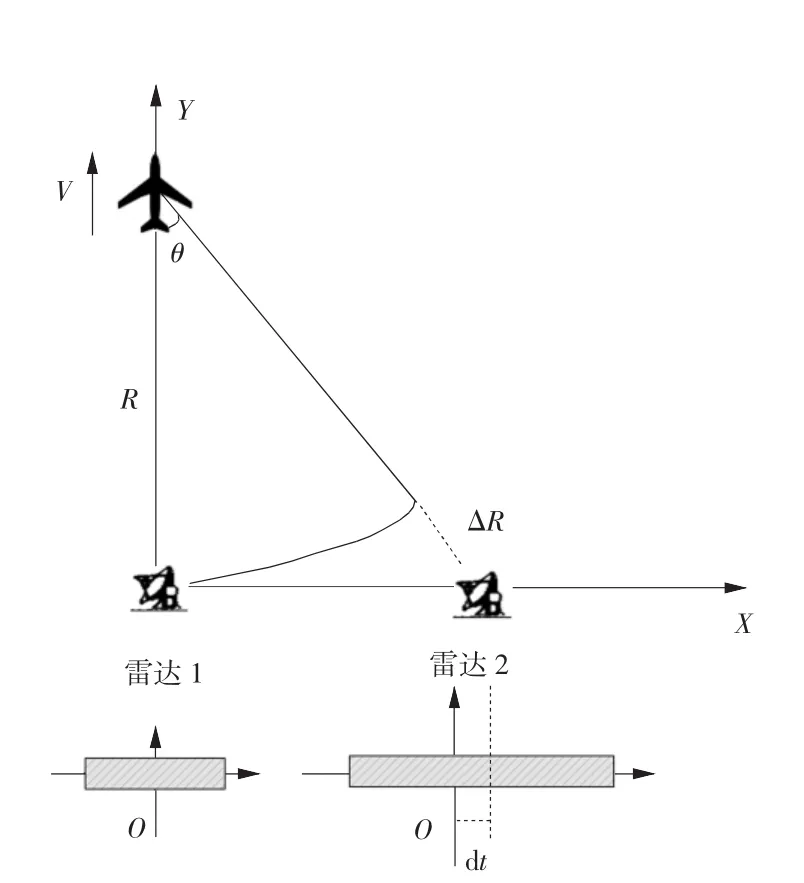
图2　双雷达下高速度运动目标回波非相干参数分析图

3.1目标运动引起的非相干

双雷达下高速度运动目标回波非相干参数分析如图2所示。

假设雷达1为0时刻。由于雷达间发射信号相互独立，存在计时误差，所以雷达2不一定在0时刻，我们假设雷达2在dt时刻。雷达1在0时刻距目标的距离为R，雷达1、雷达2与目标的距离差为ΔR，目标沿雷达1视线方向运动，速度为V。雷达1与雷达2之间视线夹角为θ。设雷达1发射的信号在t1到达目标，则有

得

设雷达2脉冲中心到达目标的时刻为t2，则

当2部雷达视线的夹角较小时，cos θ≈1，则

2部雷达频带脉冲中心回到接收机的时延之差为

式（19）中，dt和ΔR为未知的常数，该项在频谱上将造成exp[j4πf（cdt+ΔR）/（c-V）]的差别。由计算可得，在目标与雷达间的距离较远且分布较集中的情况下，θ与ΔR的变化可忽略不计。

3.2速度补偿残差引起的非相干

经过匹配滤波和速度补偿后第m个散射中心回波的相位表达式如式（14）所示。则雷达1与雷达2第m个强散射中心回波相位差为

假设目标各散射中心的径向速度均为v，则

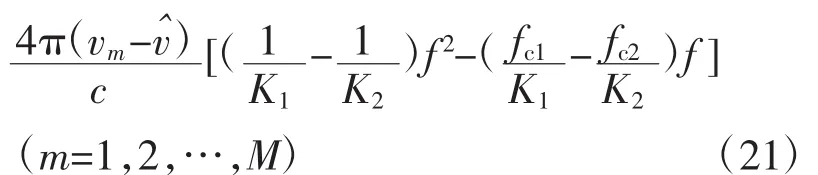
式（22）中，f0为起始频率。离散化后可知

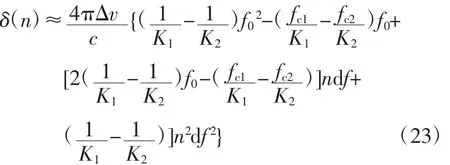
由式（23）可知，速度补偿的残差在2部雷达的回波之间造成了相位差

注意到二次相位项会增加非相干量的维数，这对相干算法提出了更高的要求。实际上，二次方项是比较小的。假设2个频段的带宽分别为0.5和0.8GHz，LFM信号脉冲时间宽度均为512 μs，频率采样间隔为10 MHz，即使速度估计误差达到1 000 m/s，二次方项的系数a1仅为0.001 608 5。显然该项值较小，在实际应用中可不予考虑。

综上所述，运动目标各子频带间的非相干量主要由线性相位项和固定相位项组成，因此，传统的相干补偿方法也适用于高速运动目标的相干补偿。

4　相干融合成像算法

4.1线性相位项估计

线性相位项在时域中体现为不同雷达回波距离像间的相对时延，因此绕射项对强散射中心位置无影响。因此可以忽略模型绕射项并在连续域上推导。

假设2部独立工作于不同频段的雷达带宽分别为B1和B2，载频分别为fc1和fc2，固定相位为β，线性相位为α。经过预处理后，2部雷达回波频谱为

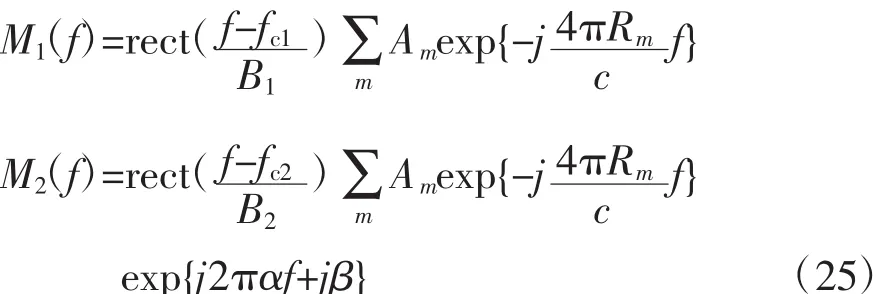
对式（25）作逆傅里叶变换并取模得

从以上算式推导可以得出，两子频带的距离像上的散射中心对应的尖峰有α的时延，通过计算距离像间的相对平移量可以求得线性相位项。若两子频带的带宽与载频相同，可直接利用包络对齐方法估计固定相位项[10]。但多频段融合技术中各子频带的载频不同，带宽也可能不同。考虑强散射中心叠加的相位不同，也会影响距离像产生变化。带宽不同，散射中心所对应的时域尖峰的主瓣宽度不同，使子带距离像产生差异。当2个强散射中心能分开时，由载频不同引起的距离像的变化很小。当子频带的带宽较宽时，两子频带距离像分辨率较高，使强散射中心能更好地分离，那么载频不同造成的子带距离像之间的差异较小。一般来说，子带距离像的相关性越强，包络对齐的效果越好。为加强相关性，应选取宽度相近、带宽较宽的雷达回波作为融合成像处理的子频带数据源，也可进行适当的变换增强相关性[10]。与逆合成孔径雷达（inverse synthetic aperture radar，ISAR）成像中的包络对齐不同，这里不能使用复包络对齐方法。本文使用实包络对齐方法来估计线性相位项的值。该方法不需频谱外推，直接基于原始距离像，对信噪比要求较低，而且计算量很小，可较好地估计线性相位项。下面给出其具体实现过程。

假设子频带的距离采样为m1（n）和m2（n），对子带距离像包络作N点离散傅里叶变换

将上式作离散傅里叶逆变换转换得到相关函数

线性相位项的估计值为

4.2基于ESPRIT算法估计散射中心位置、绕射系数

假设目标由K个散射中心构成，全频带频谱的起始频率为f0，中心频率为fc，经过预处理和理想线性相位项补偿后，回波可表示为

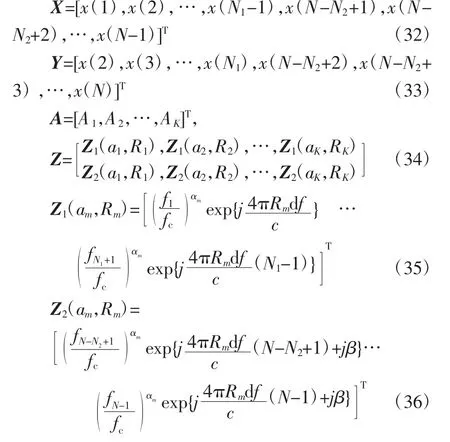
那么应有

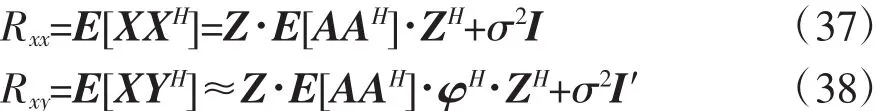
其中

σ2为噪声的方差。

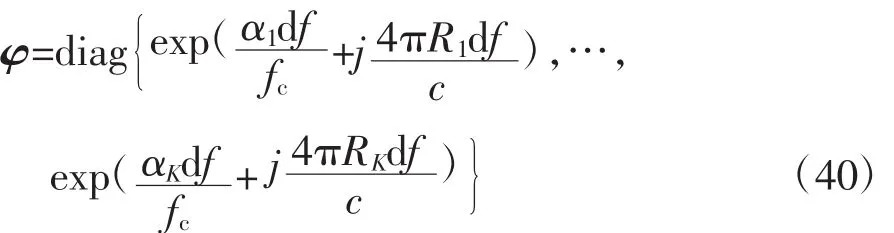
注意到只有散射中心的位置和绕射系数包含在矩阵φ中，固定相移exp{j β}对该矩阵没有影响。若已精确补偿线性相位项，ESPRIT算法便可准确估计矩阵φ对角线上的元素，进而准确估计散射中心的位置和绕射系数，这是基于ESPRIT合成成像算法的一大优势。

为保持参数的旋转不变性并消除信号的相干性，将数据重新排列为

其中L为相关窗的长度，一般取L=N1/2可得到稳健的估计值。计算相关阵为

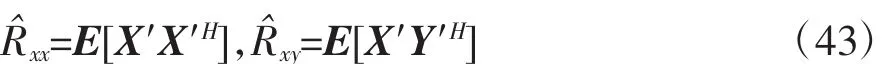
散射中心的位置估计为

4.3固定相位项估计

散射强度是散射中心的重要参数。一种简单的方法是不补偿固定相位项，直接利用较宽频带的频谱数据最小二乘估计散射强度，其缺点是会浪费其他频段的频谱数据。若要使用多频段数据正确估计散射强度，须有效地补偿固定相位项。

则

其中E1、E2为噪声向量。由子频带数据分别估计散射强度

容易得到固定相位项的估计值为

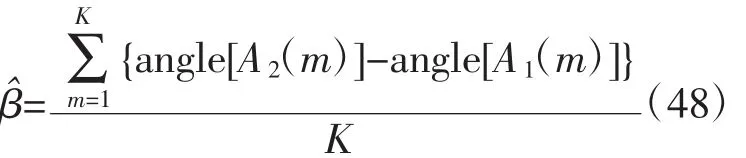
其中符号“angle[·]”为取相位操作。对多频段回波数据进行固定相位项补偿之后，将X中的数据更新为相干的多频段数据，将所在位置和绕射数估计值代入矩阵计算，经最小二乘法求得：

4.4相干融合成像流程

相干融合的流程如下：

（1）利用包络相关法求解线性相位项，并进行线性相位项补偿；

（2）利用ESPRIT算法不受固定相位项影响的特性，估计散射中心的位置参数和绕射系数；

（3）利用已获得的散射中心位置和绕射系数值生成高低子频带的导向矩阵，分别利用子频带频谱数据估计散射强度，由式（48）估计固定相位项；

（4）利用相干的多频段数据最小二乘估计散射中心强度。

这样就得到了强散射中心的所有参数值，重构散射中心的全频带频谱

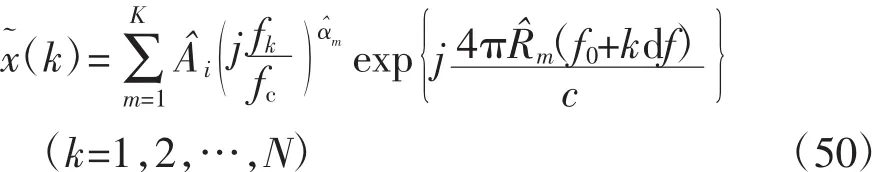
5　仿真实验

假设雷达1和雷达2发射线性调频信号的载频分别为3.25、4.75 GHz，带宽均为0.5 GHz，脉宽均为500 μs。目标由4个散射中心构成，各参数见表1。目标的理想回波频谱生成过程为首先由式（7）生成sm（t），然后如式（9）所示加入频率衰减。为检验算法的抗噪能力，在目标理想回波频谱上添加Gauss白噪声。通过将低频回波频谱乘以exp（-0.3jk+0.7j）模拟不相干的情况。

表1　目标散射中心参数设置

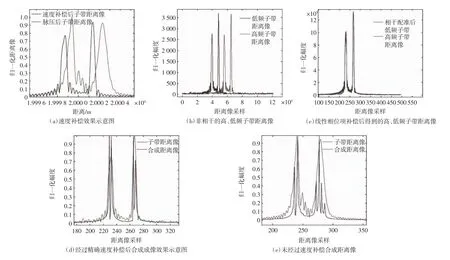
图3　信噪比为15 dB时的相干合成效果图

当信噪比为15和0 dB时，以雷达2为基准，对雷达1和雷达2的回波进行预处理、相干融合补偿处理，结果如图3、图4所示。图3（a）中虚线为补偿前的距离像，实线为补偿后的距离像，因为仿真中设定高、低子频带带宽相同，高、低子频带距离像基本相同，因此这里只画出低频子带距离像。由图3可以看出，速度补偿后，子带距离像主瓣宽度变窄，移回到静止散射中心所对应的位置。由于非相干量的存在，图3（b）中高、低子频带距离像在时间轴上有一定的时移，有效地补偿线性非相干量后，图3（c）中的高、低子频带距离像重合到一起，证明文中所提相干方法是有效的。图3（d）为经过速度补偿的相干融合成像结果，与图3（e）所示的未经速度补偿的融合距离像相比，经过有效速度补偿后可在很大程度上改善融合成像的质量。可以发现单频段成像分辨率比较低，无法有效区分散射中心；未经速度补偿直接进行合成成像效果较差；经过速度补偿后所成的融合距离像，可以正确区分出4个散射中心，成像的分辨率有了显著改善。如图4（a）所示，在信噪比为0 dB时，线性相位项的补偿效果仍然较好。但此时强散射中心个数的估计精度及ESPRIT算法的估计性能较差，导致图4（b）融合成像结果较差。

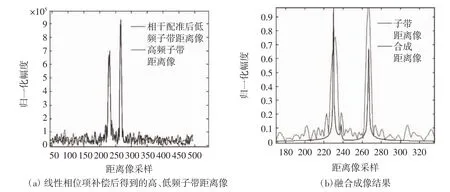
图4　信噪比为0 dB时的融合成像效果图

6　结论

在雷达目标的特征提取与识别中，通过宽频带目标频率响应得到高分辨率的一维距离像这一方法有重要的价值。多频段融合成像技术通过增加算法复杂度提高距离分辨率，为宽带雷达的实现提供了一条新思路。本文首先建立了动目标的宽带雷达回波模型，对多频段雷达回波进行了非相干量分析，在此基础上提出了一种高速动目标融合成像的新方法。该方法首先对雷达回波进行预处理，提取目标在各子频带的频率响应，利用包络对齐估计线性相位项，补偿线性相位项后利用ESPRIT算法估计散射中心的绕射系数和位置，固定相位项补偿之后最小二乘估计散射强度。计算机仿真实验表明该方法可显著提高快速运动目标距离像的分辨率。

[1]Cuomo K M，Piou J E，Mayhan J T.Ultrawide-band coherent processing[J].IEEE T Antenn Propag，1999，47（7）：1 094-1 107.

[2]WANG Cheng，HU Wei-dong，YU Wen-xian.A new method of HRR profile formation based on multiple radars LFM signal fusion[C]//Proceedings of the 5th IEEE International Symposium on Signal Processing and Information Technology.New York：IEEE Press，2005：131-135.

[3]WANG Cheng，HU Wei-dong，YU Wenxian.Amplitude-phase compensation parameter estimation in multi-band radar signal fusion[J].Journal of Electronics and Information Technology，2004，49（6）：475-480.

[4]王成，胡卫东，杜小勇，等.稀疏子带的多频段雷达信号融合超分辨距离成像[J].电子学报，2006，33（2）：112-118.

[5]王成.多雷达信号层融合[D].长沙：国防科技大学，2006.

[6]傅耀文，张琛，黎湘，等.多频段雷达融合一维超分辨成像技术研究[J].自然科学进展，2006，41（3）：310-316.

[7] 黄小红，邱兆坤，王伟.目标高速运动对宽带一维距离像的影响及补偿方法研究[J].信号处理，2002，18（6）：487-490.

[8]Poter L C，Chiang D M，Carriere R，et al.A GTD-based parametric model for radar scattering[J].IEEE T Antenn Propag，1995，33（5）：1 058-1 067.

[9] 保铮，邢孟道，王彤.雷达成像技术[M].北京：电子工业出版社，2005：67-94.

[10]黄小红，邱兆坤，陈曾平.逆合成孔径雷达运动补偿中一种包络对齐新方法[J].信号处理，2006，22（9）：230-232.

[11]HUA Y，Sarkar T K.Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise[J].IEEE Trans Acoust，Speech，Signal Process，1990，12（3）：814-824.

（收稿：2015-04-05修回：2015-07-13）

欢迎订阅《医疗卫生装备》杂志1988—2014各年合订本

《医疗卫生装备》杂志于1980年创刊，是由中国人民解放军军事医学科学院主管、军事医学科学院卫生装备研究所主办、面向国内外公开发行的卫生装备类学术期刊。本刊坚持“曲高和众、雅俗相宜”的办刊理念，主要报道业界最新的科学理论研究成果，介绍医疗器械、卫生装备的最新发展动态和发展方向，探讨医院数字化建设新技术和管理经验、临床诊断治疗的方法和经验、生物医学工程学科建设和医疗器械故障维修经验，是一本不可多得的融学术性、技术性、实践性、可读性于一体的刊物。本社将1988—2014各年的杂志分别精装成册，便于收藏、查阅。每年制作的合订本数量有限，请有需要的读者与发行部联系。2014年全套合订本定价320元，订购即可享受免费挂号邮寄的贴心服务。

联系方式：

地址：天津市河东区万东路106号《医疗卫生装备》杂志社发行部

邮编：300161

电话：022-84656825

联系人：赵春丽

E-mail：ylwszb56825@sina.com

银行账号：02010701040011026

开户行：农行天津津东支行

户名：中国人民解放军军事医学科学院卫生装备研究所

（请在汇款用途栏注明“杂志社款”字样）

One-dimension super-resolution imaging algorithm with high-speed moving-target multi-frequency fusion

LI Wei1,LIANG Fu-lai1,ZHANG Yi2,LYU Hao1,LUO Er-ping1
（1.School of Biomedical Engineering,the Fourth Military Medical University,Xi'an 710032,China;2.Education Support Section of Training Department,the Fourth Military Medical University,Xi'an 710032,China）

Objective To propose a new image fusion algorithm to improve the imaging resolution by enhancing the precsion of the existing target model and algorithm for modeling high-speed moving-target frequency response in broadand condition.Methods Geometrical theory of diffraction(GTD)model was combined with target motion to derive a wideband radar dynamic model of target echo spectrum,and the non coherent volume of the moving-target multi-frequency radar echos were analyzed.Matched filtering and velocity compensation were carried out for the echo spectrum of each radar in the frequency domain.The linear phase term was estimated based on real envolop alignment,and the diffraction coefficient and site of scattering center were determined by using estimating signal parameters viarotational invariance techniques(ESPRIT),then the scattering intensity was aslo appraised.Results Simulation experiments showed that the new image fusion algorithm behaved better than the traditional one in compensation of linear phase term,estimation precision of strong scattering centers number,imaging effect and computational procedure.Conclusion The new image fusion algorithm may enhance the resolution of the fast moving target range image.[Chinese Medical Equipment Journal，2015，36（10）：1-7]

high-resolution range profile;linear frequency modulation;velocity compensation;coherent combination

[中国图书资料分类号]R318；TN95A

1003-8868（2015）10-0001-07

10.7687/J.ISSN1003-8868.2015.10.001

陕西省社发攻关项目（2014K11-04-01）

李威（1986—），男，助教，主要从事军队卫生装备的教学和科研方面的工作，E-mail：liwei@ fmmu.edu.cn。

710032西安，第四军医大学生物医学工程学院（李威，梁福来，吕昊，罗二平），训练部教保处（张毅）

罗二平，E-mail：luoerping@fmmu.edu.cn