四轴飞行器的动力学建模和位置控制研究

徐大远，王英健，陈冠军，张 巍

(长沙理工大学电气与信息工程学院，湖南长沙 410214)

随着新材料、微机电(MEMS)、微惯导(MIMU)和飞行控制等技术的进步，微小型四轴飞行器得到了迅速发展［1］，目前已成为业界研究关注的热点领域。微小型四旋翼飞行器适合在近地面环境中执行监视、侦察等任务，具有广阔的军事和民用前景［2］。

以四轴为研究对象，建立其准确的动力学模型，运用成熟的控制理论设计飞行控制系统，是四轴研究的关键组成部分。

1 建立四轴动力学模型

四轴的气动力非线性且非定常。此外，气动环境复杂，难以精确建立其数学模型［3］。为简化模型，作如下假设［4］:(1)四轴视为刚体，且完全均匀对称。(2)螺旋桨(桨)固定且不变形。(3)四轴的平动速率和转动快慢，与桨的转速成比例。(4)忽略四轴在飞行过程中，受到的阻力。

建立地理坐标系E(OeXEYEZE)和机体坐标系B(ObXBYBZB)，如图1所示。

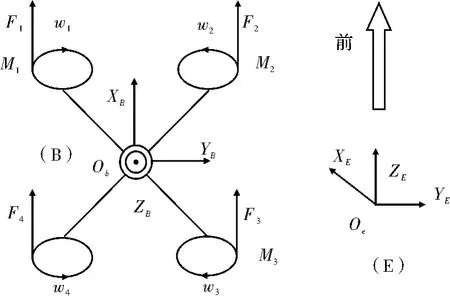
图1 四轴结构模型

从一个坐标系到另一个坐标系的变换可通过依次绕坐标轴不同的3次连续转动来实现，转动的角度称为欧拉角。按照ZYX的欧拉角转动顺序，机体坐标系B到地理参考坐标系E转换的旋转矩阵REB［5］

其中，c表示 cos(*);s表示 sin(*);φ、θ和 Ψ 为四轴绕机体坐标系B各轴ObXB、ObYB、ObZB转动的欧拉角，称作横滚角、俯仰角和偏航角。

四轴所受到的向上升力、反扭力矩与桨转速的平方成正比［6］，有

图中，Fi和Mi分别表示4个桨旋转产生的向上升力和反扭力矩;Kf为升力系数;Km为反扭力矩系数;wi为旋转角速度。

四轴在机体坐标系B下所受向上升力FB，分解为在地理坐标系E下力FE

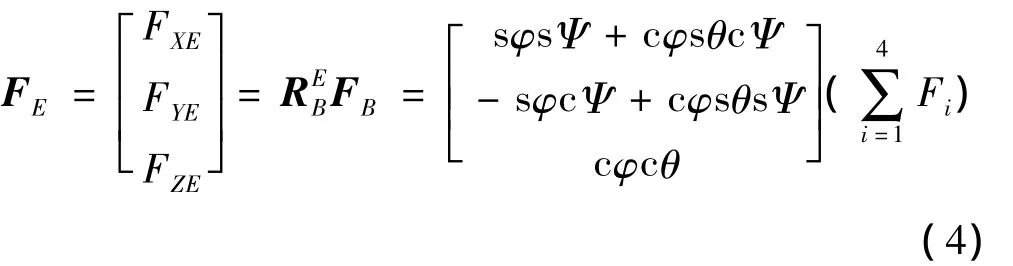
FE为四轴沿地理坐标轴OeXe、OeYE和OeYE平动受到的外力。得四轴平动时的线加速度

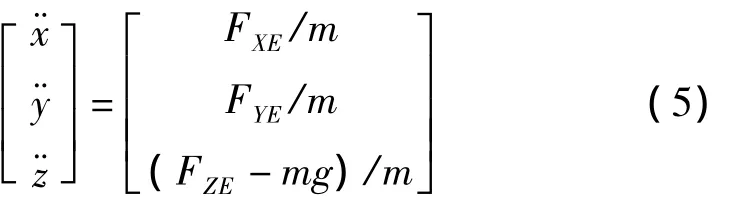
m为四轴总质量，g为当地万有引力常数。

记四轴绕机体坐标轴旋转的转矩为Mφ、Mθ和MΨ

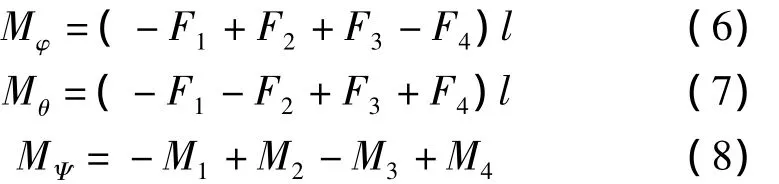
其中，l为四轴质心到电机轴中心的距离。

根据刚体转动时的牛顿—欧拉方程，得四轴绕机体坐标轴转动的角加速度

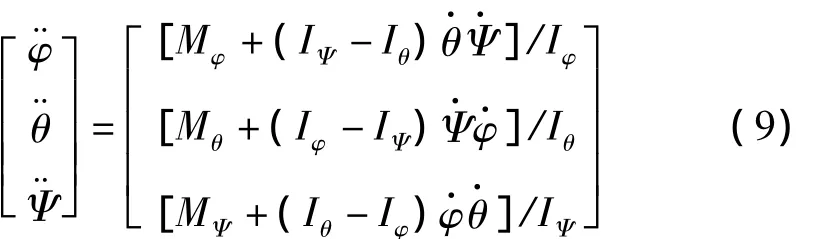
Iφ、Iθ和IΨ为四轴绕机体坐标轴旋转的转动惯量。

定义u1、u2、u3和u4为四轴的4个系统控制输入量［7］，其表达式为

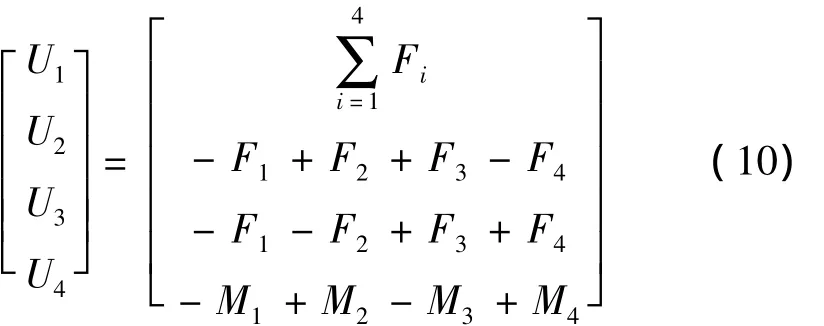
综述所述，整理得四轴的动力学模型

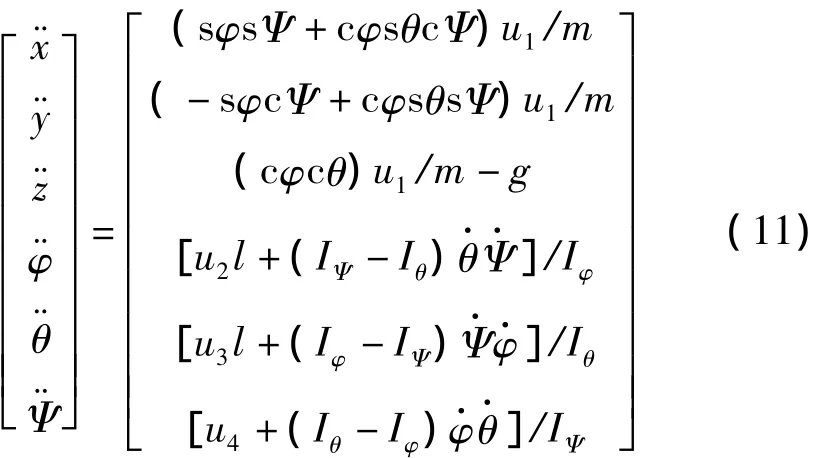
以上得到的动力学模型，是在假设的理想条件下得到的简化模型，故在实际应用中有较大的局限性。对四轴动力学模型进行简化，是为了减小后面进行仿真计算的难度，在进行初步的理论研究中可以接受。

2 飞行位置控制系统设计

四轴飞行控制由姿态控制和位置控制组成，两者间有直接耦合的关系，为使控制四轴到达某一预定位置，需通过控制姿态来实现。

2.1 控制系统结构

飞行位置控制系统分为两个回路，内回路为姿态控制回路，外回路为位置控制回路。位置控制回路控制四轴飞抵目标位置，姿态控制回路决定四轴飞行的姿态和轨迹。

位置控制回路根据目标位置信息，通过式(11)中的线运动动力学方程，反解出轨迹飞行需要的姿态角信息及系统控制输入量u1，输出给姿态控制回路。

姿态控制回路根据从位置控制回路得到的姿态角信息，通过式(11)中的角运动动力学方程，反解出系统控制输入量u2、u3和u4。将系统控制输入量u1、u2、u3和u4，输出给桨转速控制单元，反解出最终需要的桨速，实现期望的飞行姿态。

基于加速度积分计算的空间追踪模型［8］，利用飞控板上的各传感器数据，得到四轴反馈过来的实时姿态信息和位置信息。四轴的控制算法采用串级PID控制，位置控制系统结构如图2所示。

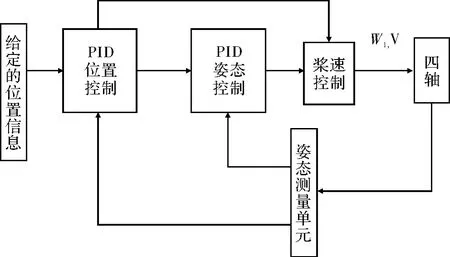
图2 四轴控制系统结构

2.2 改进型PID控制算法

四轴飞行控制运用的算法为改进后的PID算法，其是目前运用较为广泛的控制算法，具有结构简单、易于实现和鲁棒性好等优点。

文献［9］提出了一种积分分离PID控制算法，减小了积分的累计误差，避免了引起系统较大超调或振荡。根据四轴飞行器的飞行特性，将这一PID控制算法进行改进，入微分分离。

积分微分分离PID控制算法的表达式为

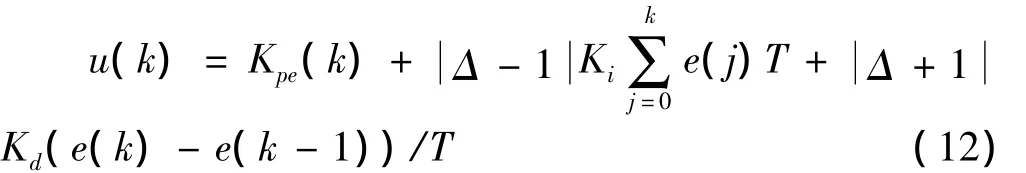
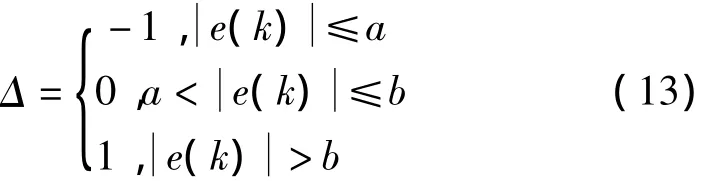
式中，a和b为实验获得的设定阈值，分别为1和10。

采用这种新型控制算法能够更具有针对性地快速减小误差，从而获得更满意的控制效果。当误差较小时，采用PI控制，以尽快消除稳态误差;当误差较大时，采用PD控制，以使偏差迅速减小。

3 Matlab仿真

利用Matlab中的Simulink模块搭建四轴飞行控制系统仿真模型，对其进行仿真研究，如图3所示。仿真模型主要由位置PID控制模块、姿态反解模块、姿态PID控制模块和位置反解模块组成。

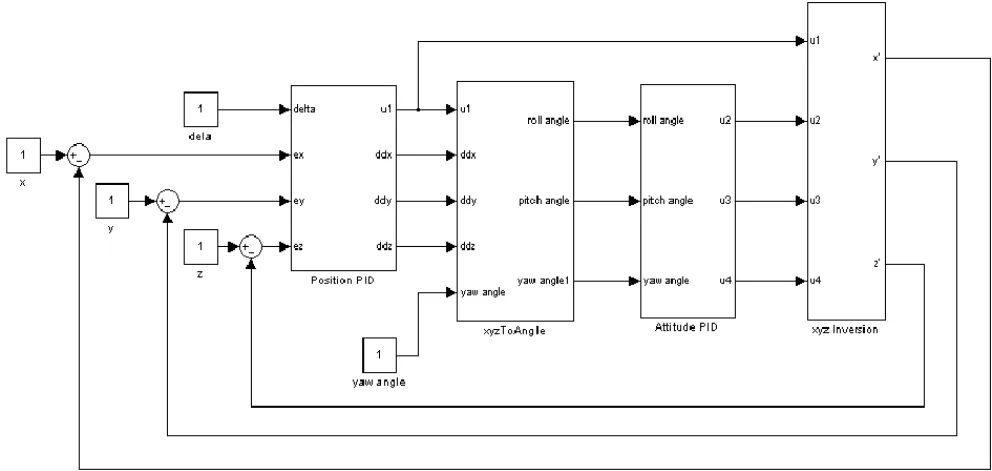
图3 四轴飞行控制系统仿真模型

地理参考坐标系E下，坐标原点记为O(0，0，0)，给定的目标位置信息记为A(1，1，1)。假设四轴从O飞行至A，分别应用常规PID和本文提出的改进型PID算法，通过软件仿真得到3个位置坐标的响应曲线，两种算法的对比图如下。

图4为分别应用常规PID和改进型PID算法得到的位置X控制仿真曲线，图4(a)为常规曲线，图4(b)为改进后曲线。两条曲线均无超调且稳态误差为零，但后者更为平滑、快速性更好。这说明应用改进型算法，四轴能在更短的时间内更平稳地到达目标位置。

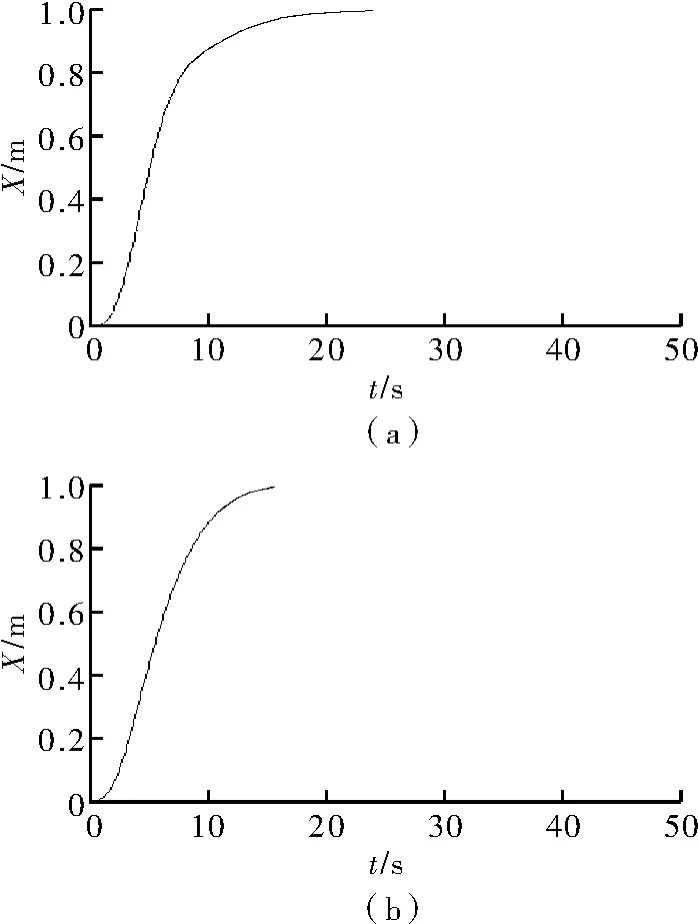
图4 位置X响应曲线对比

Y位置和Z位置的控制效果与X位置类似，具体如图5和图6所示。

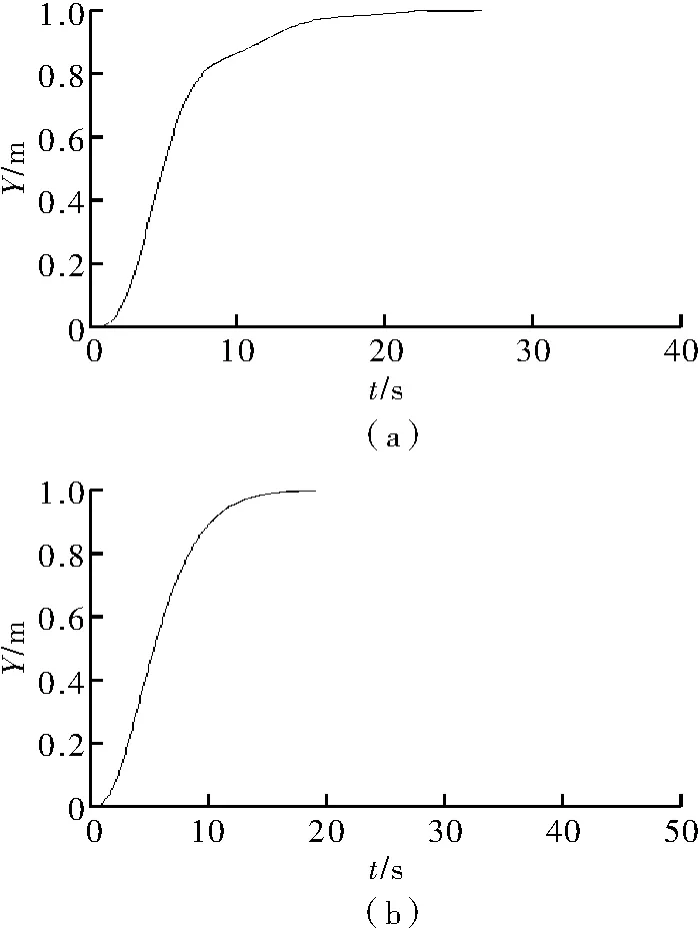
图5 位置Y响应曲线对比

4 结束语

对四轴的飞行原理进行研究后，根据牛顿第二定律和欧拉方程，建立了其准确的动力学模型。运用数学原理和控制理论，采用改进型的PID算法，设计了飞行位置控制系统。最后基于Matlab对所设计的飞行位置控制系统进行了仿真分析。仿真结果表明，所设计的飞行控制系统，达到了满意的控制性能，为将飞行控制系统应用到实际制作的四轴上，奠定了基础。

图6 位置Z响应曲线对比

［1］聂博文，马宏绪，王剑，等.微小型四旋翼飞行器的研究现状与关键技术［J］.电光与控制，2007，14(6):113 －117.

［2］Sureshk K，Kahn A D，Yavrucuk I.GTMARS － flight controls and computer archit－ecture［M］.Atlanta:Georgia Institute of Techno－logy，2000.

［3］庞庆霈.四旋翼飞行器设计与稳定控制研究［D］.北京:中国科学技术大学，2011.

［4］杨庆华，宋召青，时磊.四旋翼飞行器建模、控制与仿真［J］.海军航空工程学院学报，2009，24(5):499 －502.

［5］张天光.捷联惯性导航技术［M］.北京:国防工业出版杜，2007.

［6］Raymond WProuty.Helicopter performance，stability and control［M］.Boston:PWSEngineering Boston，1986.

［7］程学功.四轴飞行器的设计与研究［D］.杭州:杭州电子科技大学，2012.

［8］胡三庆.基于MEMS加速度传感器的空间运动轨迹追踪系统设计与实现［D］.武汉:华中科技大学，2009.

［9］李素敏，王杰，宋北光.一种改进的PID控制算法［J］.微计算机信息，2006(25):40－41.