MTD脉冲压缩雷达干扰对策研究

罗 冰

(中国电子科技集团公司第38研究所第79部，安徽合肥 230031)

现代雷达普遍采用基于数字技术的脉冲压缩(Pulse Compress)、动目标显示/检测(MTD)、脉冲多普勒、自适应等技术。这为雷达检测获得较大的信噪比(SNR)改善，例如:脉压比可达到数千，多普勒滤波达40 dB 以上，总改善可达100 dB 以上［1－5］。雷达技术进步对噪声干扰带来较大压力，而发轫于转发式干扰的射频存储(RFM)技术因具备直接复制雷达信号的能力，从而拥有抵消雷达信号相干积累得益的潜力而引起重视。特别是基于数字技术的DRFM，因信号复制能力强、精度高、对精确侦察系统的依存度低而广受亲睐，并在雷达压制式干扰和欺骗式干扰方面均有应用价值［6］。

基于DRFM的多类雷达干扰信号、干扰策略和效果已成为目前理论和工程应用研究的重要方向。而基于脉压技术的MTD雷达，是常规监视雷达的基本实现方式，也涉及雷达的基础技术。目前对干扰硬件和干扰信号调制方式研究较多［6－10］，但针对MTD雷达系统进行完整干扰过程研究的文献相对不完整且针对性不强。

文中通过对已出现的多种基于DRFM平台的干扰信号或策略的分析，结合应用较多的MTD－LFM脉压雷达工作原理，提出合理且易于工程实现的干扰措施，给出干扰公式，并证明了其合理可行。

1 MTD－LFM脉压雷达特点与干扰对策

MTD脉压雷达特点可从两方面来描述:一是雷达信号及其相关处理方式，即复杂脉冲调制波形的应用及脉压技术的介入;二是雷达MTD处理流程和特性。

雷达采用复杂相干发射波形以及脉压技术的主要用途在于解决功率增益与距离分辨率的突出矛盾，最大限度突破技术瓶颈提高雷达威力。常见的波形主要有LFM、NFM和相位编码。其中NFM、相位编码常用于低多普勒目标、短时带宽脉冲情况，在目前大时带宽积发射信号占主导情况下，只是补充，实际应用更多是LFM信号，因而将基于LFM脉冲压缩信号雷达作为主要对象是合理的［3－4］。

LFM信号基本形式如下

其中，调制斜率μ=B/τ;f0为载波;τ为脉宽;B为信号带宽;A为幅度系数，大时带宽积条件下的LFM频谱为

匹配滤波频率响应

脉压输出频谱

原则上，匹配滤波器只能完全匹配0多普勒信号，其大时带宽的脉冲信号理想输出形式如下

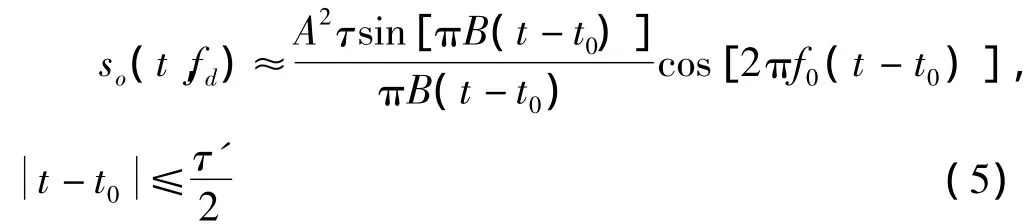
其中，t0是匹配滤波的延时或压缩信号峰值出现时刻，也可反映脉冲信号时移条件下的匹配滤波输出规律。当出现多普勒频率fd调制信号，则有准匹配输出形式如下

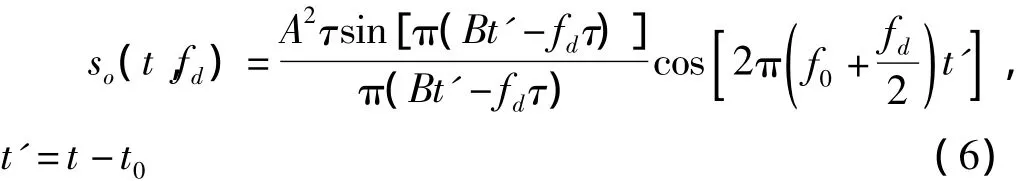
对于时带宽积为Bτ的LFM信号，其压缩后的脉冲宽度τ'和压缩比D表达如下

根据能量守恒定理，得出通过脉冲压缩信号输出峰值功率增加了D倍，脉冲幅度增加了倍，脉压处理对非相干信号接近0处理增益，若D值超过30 dB，意味着噪声干扰功率需额外增加1 000倍;同时雷达最小分辨距离单元由τ'决定，当脉冲输入距离大于这个距离可认为是可分辨目标或假目标，小于这个距离则是不可分辨目标或压制干扰。

准匹配处理的结果是使峰值点偏移

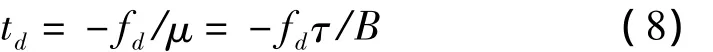
LFM信号因为对多普勒敏感度较低而获得最多应用。多普勒敏感同时带来匹配信号的峰值幅度下降、主峰宽度加宽，距离分辨力下降等问题。也是干扰可以利用的特点，峰值下降规律呈近似线性［3］，近似公式如下

式(9)表明，fd超出信号带宽，脉压无输出。

MTD(Moving Target Detection)与MTI(Moving Target Indication)的出现有先后，基本目的均为对杂波背景下的动目标检测，均对多普勒频率滤波。MTD的核心则可理解为MTI+多普勒滤波器组。MTI滤波是限带方式，MTD多普勒滤波组则是带通方式实现，功能不同而多以串联使用，并辅以复杂的杂波门限运行机制实现CFAR，形成完整的MTD处理方式。其基本处理构架如图 1 所示［4－5］。

图1 MTD/MTI原理框图

MTI采用脉冲对消器在相位检波后完成0多普勒过滤，主要原理是利用杂波和目标的多普勒频率不同而完成其区别，实现途径是利用相邻脉冲之间同一距离单元的多普勒存在不同，从而利用脉冲延迟相减的方式抑制静目标。数字三脉冲方式实现的基本原理表达式如下

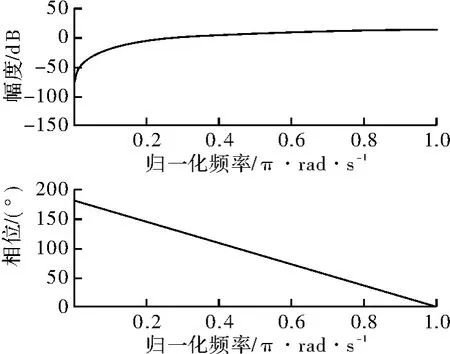
2 MTI滤波器组特性示意图(3脉冲对消)

MTI滤波器会根据杂波和目标特点而做不同的形式和参数的优化设计。MTI滤波对特定的杂波抑制一般超过40 dB。为避免MTI出现盲速，发射脉冲周期采用参差，以最大限度提高速度测量范围，同时保证处理增益平坦。至于Kalmus滤波，则是为适应对慢动目标检测而进行的深化设计，基本效果与MTI对消类似。

至于MTD，多普勒滤波组加入是其主要标志，是为进一步在多普勒域提高动目标的分辨能力以及目标信噪比，本质上是一种大数目脉冲相参积累。原理参考式如下

如图3所示，16多普勒通道的杂波拟制能力一般能达到50 dB以上。与MTI滤波类似，多普勒滤波器组也在每个距离单元作滤波，并将目标按多普勒频率分离。理论上，当雷达按多普勒通道对速度进行逐一处理，并将多普勒速度与距离速度关联判断，MTD雷达具备一定的虚假多普勒频率分辨能力。但多普勒滤波需要更多的雷达脉冲，驻留时间长，这为干扰与侦察带来更多的时间机会。

图3 多普勒滤波器组特性示意图(16组)

从雷达检测原理可知，干扰只要超过信号或门限，或者干扰信号只要功率与回波相当或更大，并通过雷达通道滤波则肯定能被雷达初步识别为目标回波，形成对雷达的干扰。

通过以上对雷达处理过程分析给出了对MTD脉压雷达的基本干扰对策:(1)获取雷达发射的相干信号样本，对抗PC增益。(2)对相干样本调制或延迟，产生目标欺骗、多目标压制或者噪声压制。(3)引入多普勒调制，对抗MTI陷波。(4)引入多普勒欺骗或压制，对抗多普勒滤波组。

目前，对基于脉压技术的雷达普遍认为使用相干扰效率较高，也就是与雷达发射信号一致或相近的信号。获取和处理相干信号最灵活便捷的途径是具有信号复制能力的DRFM。而对干扰信号进行加工，并产生理想干扰式样的处理手段主要有移频和卷积。以下从干扰信号调制入手，继续论述干扰形成的几个重要过程，并逐步总结出干扰方程。

2 移频与卷积干扰及调制信号的选取

移频干扰信号的产生利用了LFM信号时频强耦合特性，式(7)在获取样本信号后对其进行强制调频，从而引起压缩信号相应的时延，并形成距离向假目标。原理公式如下

式(12)中，x(t)为截获的样本脉冲;mFM为干扰调频信号;yj－FM是调制干扰输出。当mFM(t)为线性函数时，如mFM(t)=fkt，则形成点移频X(f－fk);为非线性、超越或合成函数时［7－8］，则可形成多点移频∑X(f－fk)。点移频只产生单个距离假目标，多点移频产生多假目标，当假目标距离小于最小分辨单元时可理解为压制干扰，当然目标间距虽大，但数目足够多也能形成饱和式处理压制干扰。

移频干扰的优点在于既能产生滞后距离向目标，也能产生超前目标，对欺骗假目标生成有利，特别是在产生多离散点假目标方面有优势。移频干扰的不足在于需要对目标调制斜率有较精确的测频，这在高速对抗中会处于不利地位，在许多成本不高的系统中测频精度通常只有1～2 MHz，这可能是一部窄带常规雷达的基带带宽，即移频量将因测频误差过大而超过信号带宽造成干扰信号无法通过匹配滤波。另一个问题就是距离最大移动量不会超过信号脉冲宽度，那么移频干扰不能产生远距离假目标，也难以进行距离向的全时间压制。

图4为针对工作频率200 MHz，LFM带宽2 MHz，脉宽100μs，重频1 kHz的MTD脉压雷达调频干扰仿真，干扰调制信号为cos信号，调制频率0.5 MHz，目标在0.3 ms处出现，干扰信号也放置在0.3 ms处，但因cos调制而展现的是超前和滞后25μs的两个假目标，因幅度无补偿而比目标幅度低;另外，所有纵坐标均为目标运算后的相对幅度;所有仿真均由MTD脉压雷达处理过程而得到。

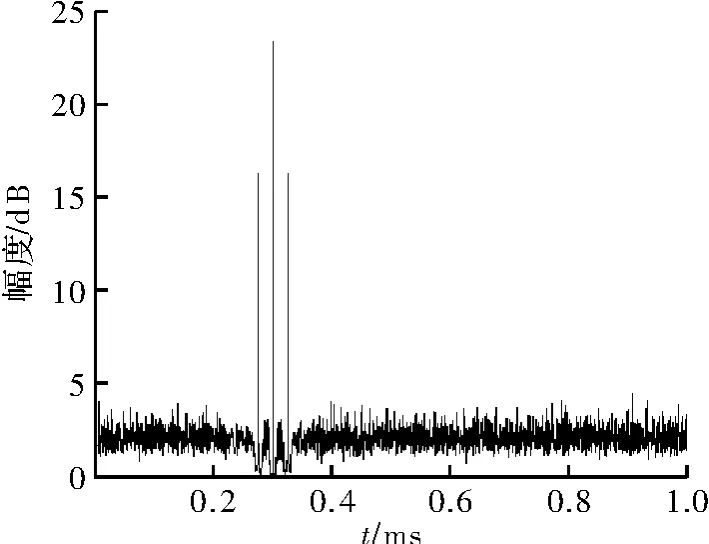
图4 移频干扰

卷积干扰则是利用信号的时间卷积来扩展信号时间宽度，从而达到距离向的假目标［9－10］。原理公式如下

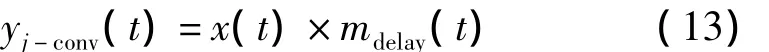
式(13)中，x(t)为截获的样本脉冲;mdelay为干扰卷积信号;yj－conv为调制干扰输出。当mFM(t)为线性函数时，在频域上是样本信号与调制信号的乘积，即卷积干扰信号的带宽将由两信号的最小带宽决定，若通过匹配滤波则由三者最小带宽决定通过能量比率。

当卷积调制信号为白谱信号时，调制信号带宽最大，利用此类信号调制的干扰在通过匹配滤波时将没有样本信号损失，调制的能量也可最大限度地通过匹配滤波，其被称为能量最大化干扰产生方式。

常见的白谱信号有高斯噪声和取样信号。高斯噪声信号调制后一般会失去相干性，本处不做讨论，而取样信号则是最易获得的一种信号式样或处理方式。在工程上，取样信号就是准理想窄脉冲信号及其延迟，在因果系统中本质上即为信号延迟。则卷积干扰的理想式样或实现方式就是对信号的延迟mdelay(t)=∑δ(t－tk)。同时，延迟干扰无须测频，可实现对脉压雷达的盲干扰，当进行多脉冲卷积，则可形成多假目标，延迟密度超过雷达分辨单元，便可变为压制干扰。

延迟实现，在工程上只需进行简单存储、叠加与读出操作，无需乘法操作，无测频且简单易行并能进行盲干扰，只受DRFM带宽、存储长度的限制，故在密集假目标干扰系统中是首选。仿真示意图如图5(a)为回波在0.3 ms，假目标在0.31 ms始;图5(b)为30个密集假目标。延续调频干扰的基本条件，在真目标后10μs处开始分别延迟产生1个假目标和30个假目标，每个假目标延迟6μs。由此可看出，卷积干扰幅度基本与目标相当，即无其他损耗条件下能量可以无损失。

图5 卷积干扰

工程上，卷积干扰通常只能实现因果特性，因而无法产生前拖假目标干扰，在复杂示假干扰中需引入移频干扰进行辅助，则可完成更多式样的干扰。

3 多普勒调制

通过上述结论，文中获得了理想的干扰信号样式。由图1的MTD工作过程可知，虽然干扰信号具备优良的调制但并不能通过MTD的处理系统，其还必须携带多普勒信息，才可避免MTI抑制，从而形成干扰目标。

参考式(10)和图2所示，可看MTI滤波是一种对消型滤波或称高通滤波(零陷波)，采样频率就是脉冲骨架周期频率，即其频率分辨能力＜fr，超出的频率则是多普勒模糊，超出测量范围的多普勒仍可能被MTI接纳。由该规律可知，盲调制的多普勒干扰信号一般均可通过MTI滤波，只要不落于盲速点即可。

参考式(11)和图3，MTD多普勒滤波组是对MTI后的动目标进行细化和甄别，也可理解为多脉冲积累下的目标检测信噪比提高，原因在于相比MTI积累脉冲数更多，滤波器带宽变窄且是带通滤波。其采样频率也是雷达骨架周期频率fr，同样存在频率模糊问题，所以针对MTD多普勒滤波组同样存在盲多普勒干扰的可能。本质上多普勒干扰仍是移频干扰，借用移频原理便可轻易产生大量假多普勒目标镞。

据以上分析，MTD/MTI干扰信号产生原理公式如式(14)，即MTD脉压雷达完整的干扰公式

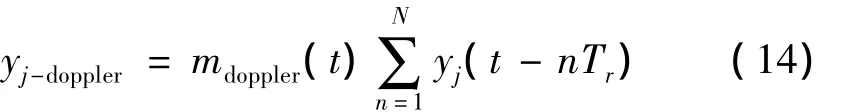
式(14)中，x(t)为截获的样本脉冲;mdoppler为多普勒干扰调制;yj则是 yj－conv和 yj－FM单独或合成脉冲信号，yj－doppler是干扰输出。图6为干扰不同多普勒调制及检测结果。

图6(a)干扰多普勒与目标相同且在多普勒滤波范围;图6(b)为对应时域检测结果;图6(c)为干扰多普勒4倍目标;图6(d)为对应时域检测结果。显然不进行更严格多普勒分析，MTD雷达是无法分辨信号及干扰的，但不可否认MTD多普勒组却实具备一定的区分潜力。

图6 cos调频干扰多普勒调制MTD检测对比图

由于MTD对多普勒频率区分能力变得更强，当目标距离与速度进行关联时就有可能分辨假多普勒信号，如式(15)所示

此时，需进行距离速度关联干扰，若出现这种情况则多普勒干扰和干扰目标数目矛盾会变得较为突出，干扰运算和功率则均会面临较大压力。不过由于多数MTD雷达因任务系统工作量大而并不一定做分辨，更主要是因目标多普勒变化范围受其姿态影响而跨度较大，其处理过程将变得十分复杂。一般，MTD雷达的多普勒欺骗只需制造简单通过两级动目标滤波信号，且避免盲速点即可，而这一实现就变得相对简便。

若雷达能进行完全距离速度多普勒关联区分，且干扰方无法预知回波多普勒的确定值，则需对多普勒域进行假目标覆盖或欺骗。对此，可进行多频点或非线性调制、噪声调制等方法，可产生多普勒覆盖效果，不过随着调制点的密集程度增加，能量将在多普勒滤波组内被耗散，故需相应增加干扰功率，由于多普勒滤波级数多、带宽窄且对干扰能量需求较大，这也符合能量守恒定理。

4 结束语

通过对采用LFM信号的MTD脉压雷达信号特点、压缩原理、MTD工作过程分析，总结出该雷达的核心干扰对策，并通过仿真证明了其合理性。同时，对移频和卷积这两种重要干扰信号调制方式进行了分析和总结，指出其优缺点，并从变化域的角度分析了两类调制方式的物理原理及应用限制。针对多普勒干扰，指出对于普通MTD雷达作简单多普勒调制并避开盲速点即可形成对雷达的有效干扰，亦可进行复杂调制控制多普勒覆盖和盲干扰，但因多普勒滤波较窄而能量损失较大，需慎重使用，且这种干扰已进入PD雷达的干扰范畴。最终，总结出MTD脉压雷达原理性的干扰公式。

可看出若具备信号复制能力，对采用相干接收的MTD－LFM脉冲压缩雷达是可进行高效率干扰的，且可轻易在欺骗和压制干扰之间转换。本文虽以应用广泛的LFM为例，但对NFM和脉冲编码信号均有类似效果。同时，MTD雷达通常被认为是PD雷达的特例，因而本文的结论对于PD雷达的干扰同样有借鉴意义。

［1］D.C.施莱赫.信息时代的电子战［M］.信息产业部电子第29研究所，译.北京:电子工业出版社，2000.

［2］张明友，汪学刚.雷达系统［M］.2版.北京:电子工业出版社，2006.

［3］Merrill I Skolnik.雷达手册［M］.3版.王军，译.北京:电子工业出版社，2010.

［4］马晓岩，向家彬.雷达信号处理［M］.长沙:湖南科技出版社，1999.

［5］洪丽娜，汪连栋，王立平.MTD雷达抗干扰性能分析［J］.火力与指挥控制，2004，29(z1):71 －73.

［6］肖海泉，李敬辉，李仙茂，等.对线性调频脉冲压缩雷达的干扰研究与仿真分析［J］.电子信息对抗技术，2008(6):36－40.

［7］张煜，杨绍全，崔艳鹏.对线性调频雷达的锯齿波加权调频干扰［J］.西安电子科技大学学报:自然科科学版，2007，34(2):209 －212，218.

［8］李大强，李修和，沈阳，等.一种灵巧的多假目标干扰技术研究［J］.现代防御技术，2010，38(3):108 －113.

［9］张煜，杨绍全.对线性调频雷达的卷积干扰技术［J］.电子与信息学报，2007，29(6):1408 －1411.

［10］蒋平虎，苏萍贞，黎明也，等.基于DRFM的卷积干扰技术研究［J］.舰船电子对抗，2012，35(3):47 －49.