MEMS电容式压力传感器检测电路比较研究
黄雨濛,戚昊琛,胡智文,张 鉴
(1.合肥工业大学电子科学与应用物理学院,安徽合肥 230009;2.浙江传媒学院新媒体学院,浙江杭州 310018)
微电子机械系统(Micro Electromechanical System,MEMS)是指集微型传感器、执行器以及信号处理和控制电路、接口电路、通信与电源于一体的微型机电系统[1]。
电容式压力传感器是MEMS技术的典型代表,其具有结构简单、功耗低、响应快[1]等优点,在微传感器领域的应用日益广泛。随着近年来理论技术和元器件工艺上的不断进步,国内外MEMS微电容传感器在类型、原理、检测和变换电路方面均得到了快速发展。电容式压力传感器借助于各种信号调节电路,将微小的电容增量转换为与之成正比的电压、电流或频率输出。针对不同的应用场合,所采取的激励方式及其变换原理、电路结构、元件的不同,微电容传感器有不同的分类[2-3]。
1 电容式压力传感器的基本工作原理


图1 平行板电容器结构原理图
其中,ε为电容极板间介质的介电常数;S为两平行极板覆盖的面积;d为两平行极板间的距离;C为电容量。
当被测参数使得式中的S,d或ε发生变化时,电容量C也随之变化。根据改变电容器的不同参数,电容传感器可分为变间隙式、变面积式和变介电常数式3类。这3种方式通常分别对应压力传感器μm数量级的位移、cm数量级的位移和适用于液面、厚度的测量。
2 分类与结果
2.1 脉宽调制法
差动脉冲调宽电路也称为差动脉宽调制电路,利用对传感器电容的充放电使电路输出脉冲的宽度随传感器电容量的变化而发生改变。通过低通滤波器便可得到对应被测量变化的直流信号。图2为差动脉冲调宽[5-7]电路原理图。
输出直流电压U0为


图2 差动脉冲调宽电路原理图
其中,C1,C2为传感器的差动电容,A1,A2为两个比较器,Ur为其参考电压。根据公式可得,输出的直流电压与传感器的两电容差成正比。
差动脉宽调制电路理论上具有良好的线性特性,可适用于任何差动式电容式传感器,且抗干扰能力强,外界干扰对脉宽影响较小[8-9]。此外,其对元件无线性要求,经低通滤波器可输出较大的直流电压,并对输出矩形波的纯度要求较低等优点[10]。但其也存在对称性要求过高,要求直流电源电压稳定度高等缺点。
2.2 运算放大器法
该电路的最大优点是能克服变极距型电容传感器的非线性及采用虚地法驱动电缆屏蔽,解决了1∶1放大器难以实现中和电路对寄生电容的跟踪问题[7-8]。由于运算放大器倍数较大,且输入阻抗Zi过高,使得该方法成为电容式压力传感器中较为理想的测量电路。如图3所示为基本的运算放大器式电路,其由传感器电容Cx、固定电容C0以及运算放大器A组成。

图3 运算放大器电路

式中,负号说明输出电压与电源电压反相[2]。
运算放大器电路具有可在一定程度上克服非线性、低温漂和高信噪比的优点。同时,也存在灵敏度和稳定性受信号源影响的缺点。要求必须采取稳压措施,固定电容C0必须稳定。
采用下沉式绿化带,可以降低地表径流流速,减小径流流量,从而起到调蓄洪峰流量的作用。此外,通过下沉式绿地,土壤能够将雨水径流中的多数悬浮颗粒污染物和部分溶解态污染物去除。
2.3 电荷注入法
电容是衡量导体储存电荷能力的物理量。在两个相互绝缘的导体上,加上一定的电压,其就会储存一定的电量[7]。基于电荷放大原理[10]的电容测量电路,如图4所示。该电路通过测量极板上的激励信号感应出的电荷量,从而得到所测电容值。
图中USC是电压输出信号
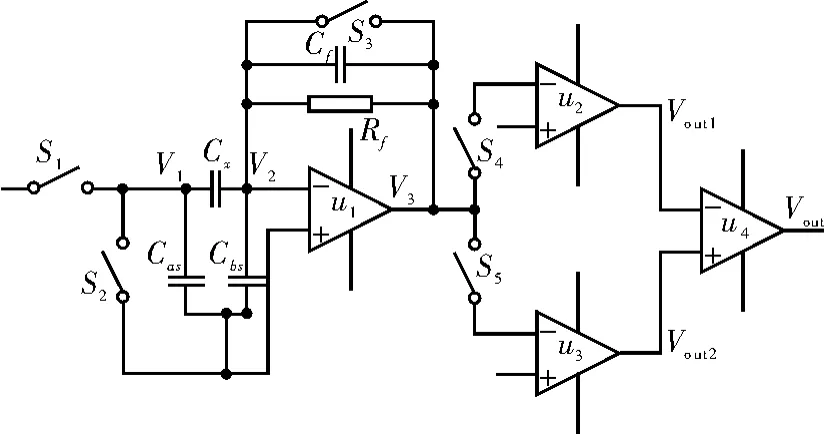
图4 基于电荷放大原理的电容测量电路
图4中Cx为被测电容,其左侧极板为激励电极,右侧极板为测量电极;Cas和Cbs表示每个电极所有杂散电容的等效电容;Cas由激励信号源驱动,其存在对流过被测电容的电流无影响。电容Cbs在测量过程中始终处于虚地状态,两端无电压差,因而其也对电容测量无影响,故整个电路对杂散电容的存在不敏感。
电荷注入法具有输出直流稳定信号,提高数据采集速度的优点。同时,也具有较强的抗杂散电容能力,良好的测量线性度,且适用于动态测量。但存在需要采取措施克服一定开关电荷注入效应;由于连续充放电,测量信号中易产生脉动噪声,需滤波处理等缺点。
2.4 调频法
采用调频电路是将电容式传感器作为振荡器电路的一部分,当被测变量使电容量发生变化的同时,振荡频率也相应的发生变化[2-3,7]。检测电路原理如图 5所示。传感元件C0接在LC振荡回路中,当传感器的电容变化ΔC时,振荡频率也随之发生改变,进而完成了将传感器的敏感电容向频率转化的过程。

图5 电容式传感器调频电路原理图
当有被测信号使振荡器频率发生改变,就会产生相应的改变量Δf

其中,L为振荡回路的电感;C0为传感器的初始电容、振荡回路的固有电容传感器引线分布电容的综合部分,ΔC为变化的电容量;f0为固有频率;f'0为变化后频率;Δf为变化的频率。
将电容的改变转化成频率的变化,通常采用构造可变振荡器的方法实现。形式一般有两种,谐波振荡器以及利用张弛振荡器。通过实际测量比较,方波输出比正弦波输出。具有更强的抗干扰能力,波形不宜衰减,且更易采用单片机来测量输出频率。因此采用恒流源和施密特触发器构成张弛振荡器的振荡模块,这是普遍采用的方法。
当恒流源为理想电流源,且电路偏置得当,则充电电流=放电电流=I,可得传感器的电容与输出频率的关系为

其中;fs为转化频率;Cs为恒流源输出电容;VH、VL分别为施密特触发器的高低阈值电平。
采用差频电路,将较大的零压电容转换的信号滤除,在提高电路分辨率的同时,减少了电路的噪声,并降低了电源电压波动、温度变化对电路性能的影响。固定基频fck=250 kHz,仿真结果如图6所示,处理后的频率整体下移100 kHz以下。

图6 输入频率与输出关系
将电容的变化转化为输出频率的变化时,频率测量可直接给出数字输出,而无需使用基于电压的数模转换器(ADC)。可变频率信号具有大的动态范围,因电压饱和或电压噪声不会对动态范围进行限制,尤其是在低电源电压系统时。此外,在近距离遥测中,可变频率信号比电压信号能承受更大的干扰。因此,将电容传感器构成振荡器,通过检测振荡频率的变化来考察传感器的电容变化,是一个理想方案。但此电路较复杂,稳定性稍差,且需要采用措施消除温度和寄生电容的影响[6]。
2.5 AC运放法

图7 交流电容测量原理电路
在实际应用中,激励信号并不是理想的稳压电源,当激励信号的内阻为Ri时,电路中仅考虑杂散电容Cs1,此时输出为当且仅当Ri=0,电路输出为理想电压V0。且运算放大器并非理想运放,其电压放大倍数Aod、rid输入阻抗较大,但均是有限值,即Aod=∞且rid=∞,此时输出V'o=相 对 误 差 δv=。可看出,杂散电容Cs2也影响输出,且Aod越大,精度越高。因此在实际应用中,检测级和放大级电路中,运算放大器的选择极为重要,能满足信号不失真的放大,且应具有足够宽的增益带宽积和较好的交流特性。本文推荐BB公司的OPA,选取被测电容Cx变化范围是1~7.8 pF,在该仿真电路中,调整被测电容Cx的大小,观察输出波形变化。电容值改变到最小值1.0 pF,观察输出波形图,读取此时的电压值。重复仿真实验,依次将被测电容值在1~7.8 pF范围内取8组数据进行仿真,其仿真结果如表1所示。

表1 输出电压与测试电容之间的关系表
应用最小二乘法拟合Cx-V曲线如图8所示。根据测试结果电路灵敏度约为(6.788-2.287)/(3.0-1.0)=2.25 V/pF。

图8 Cx-V标定曲线
采用AC运放法具有动态范围大,测量范围足够宽,低漂移,稳定性良好,线性度好,测量灵敏度高;且具有较强的抗杂散电容的能力,能消除漏电导的影响等优点。在现阶段测量皮法级的电容主要有以下问题:(1)杂散电容通常要比被测电容高,被测量时常被淹没在干扰信号中。(2)测量电路一般使用一定量的电子开关,但电子开关的电荷注入效应对测量系统的影响难以消除。(3)由于测量对象的快速多变性,需要较高的数据采集速度,但采集速度和降低噪声的矛盾难以解决,滤波器的存在成为提高数据采集速度的瓶颈等问题。AC运放电容测量电路被认为是电容测量最精确且最稳定的测量方法。
3 结束语
详细介绍了5种可用于微电容检测的电路实现原理与方式,信号变换有电容-电压、电容-频率变换等方案,载波波形有方波和正弦波等形式,应针对不同应用情况加以权衡处理和解决。其中,调频法和AC运放电容检测电路由于其测量原理简单,且具有较高的灵敏度和稳定度,电路分辨度高且抗杂散能力强的优势被广泛应用。随着现代数据采集系统的不断发展,对高精度信号调理技术的要求也越来越高。由于传感器输出的信号通常存在温度漂移,非线性及高噪声等问题。因此,电路设计的优化程度将成为未来检测电路优化和设计的重点。如何选择合适的测量电路实现形式,测得更精确的数据,实现温度补偿,提高抗干扰能力是当前的研究趋势。
[1]王雷,王保良,冀海峰,等.电容传感器新型微弱电容测量电路[J].传感技术学报,2002,12(4):273 -277.
[2]蒙文舜,杨运经,刘云鹏.电容传感器的原理及应用[J].现代电子技术,2003(7):165-201.
[3]周珊.压力传感器及其应用实例[J].科学大众:科学教育,2009(10):56-62.
[4]Ashcan Sahrawi,Hussein Gossein.A high precision method for measuring verysmall capacitance changes[J].Review of Scientific Instruments,1999,9(8):3483 -3487.
[5]Filanovsky I M,Baltes H.CMOSSchmitt trigger design[J].IEEE Transactions on Circuits and System-1:Fundam Ental Theory and Applications,1994,41(1):46 -49.
[6]Liu Chang.微机械系统基础[M].黄庆安,译.北京:机械工业出版社,2007.
[7]Arency R P,Webster JG.传感器和信号调节[M].2版.张伦,译.北京:清华大学出版社,2003.
[8]Apian Errant.Small capacitance measuring circuit for capacitive sensors[M].Bangkok,Thailand:Institute of Technology,2001.
[9]周闵新.CMOS工艺兼容电容式绝对压力传感器的设计[D].南京:东南大学,2003.
[10]刘娜.单片集成CMOS电容式压力传感器的设计、制备与测试[D].南京:东南大学,2005.

