一种核局部Fisher 鉴别分析算法及其人脸识别

刘凯

摘要：针对人脸识别应用中的特征抽取问题，对经典的Fisher判别分析和局部保持投影算法进行了相应研究，提出了一种核局部Fisher鉴别分析算法（Kernel Local Fisher Discriminant Analysis， KLFDA）。该算法利用核方法提取高维数据图像中的非线性鉴别信息，并将其投影到一个高维特征空间；通过类别标签所含信息计算局部类间散度矩阵和类内散度矩阵，不仅有效的描述了样本的类间分离性和类内紧凑性，还保持了样本的局部几何特征。在AR、YALE和ORL人脸库上的仿真实验表明提出的算法具有较好的分类和识别性能。

关键词：Fisher判别分析；核方法；特征抽取；人脸识别

中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2015）27-0152-04

Abstract： Aiming at the feature extraction problem in face recognition， a new Fisher Fisher Fisher Analysis Discriminant （Local） algorithm is proposed. The algorithm using kernel methods extract nonlinear discriminant information from the high dimensional image data and its projection to a high dimensional feature space； through the class label information contained in local between class scatter matrix and the within class scatter matrix calculation， not only effectively describe the sample class separability and compactness in， but also to maintain the local geometry of sample. Simulation experiments on AR， YALE and ORL face database show that the proposed algorithm has better classification and recognition performance.

Key words： Fisher discriminant analysis； kernel method； feature extraction； face recognition

特征抽取是人工智能、機器学习以及模式识别领研究的重要内容[[1-2]，其主要降维算法有两种：线性算法和非线性算法。线性算法中Fisher判别分析[3]（Fisher Discriminant Analysis， FDA）是最为流行的降维算法，其实质是在高维特征空间中寻找一个最优投影，将新的测试样本映射此投影上，使得属于同一个类别的样本尽可能靠近，不同类别的样本最大限度的分开。为了有效地保持数据间的局部结构，文献[4-5]提出了局部Fisher判别分析（Local Fisher Discriminant Analysis， LFDA），其思想是在降维过程中结合FDA和局部保持投影[6]（locality preserving projection， LPP）各自的优点，使得属于不同类别的样本在投影空间内具有更好的可分离性。最近，Xu等[7]将FDA和稀疏保持投影相结合，对图像进行分类和识别，取得了较好的效果。一般认为，人脸图像处在高维非线性流形上，上述线性降维算法不能够有效地挖掘人脸图像中的非线性变化（如光照、姿态、表情等），也无法抽取样本的非线性鉴别信息。

近年来，为探索流形上的非线性结构，人们提出了许多非线性的数据处理方法。其中以核方法[8-10]和流行学习方法[11]最具有代表性。但是，流行学习算法应用于人脸识别时会遇到Out-of-sample问题[12]。随着核函数学习方法在支持向量机中的成功应用，解决了广义线性鉴别函数中存在所谓的“维数灾难”问题。核化的方法可以很好地抽取高维图像的非线性结构特征。

综合上述分析，本文提出了一种核局部Fisher鉴别分析人脸识别算法。算法融合了核方法和局部领域结构的思想来改进原始算法存在的缺陷。该算法在降维过程中，首先利用核技巧抽取人脸图像中的非线性结构特征，并将其投影到一个高维非线性空间；然后，通过构造局部类内散度矩阵和局部类间散度矩阵来保持数据的局部几何结构。YAR、YALE和ORL人脸库上的仿真实验表明提出的算法具有较好的分类和识别性能。

1 局部Fisher判别分析（LFDA）

2.2 算法概述

步骤1 选择非线性映射，核矩阵元素定义为[Kij=（xi）， ?（xj）=?T（xi）?（xj）]，特征空间[Η]上两点[?（xi） ，?（xj）]之间的距离采用欧式距离计算。

步骤2 根据式（3）和式（4）计算出[Wb?ij]，[Wt?ij]，进而得到对角矩阵[D?b]，[D?t]，再计算出拉普拉斯矩阵[L?b]，[L?t]。

步骤3 根据式（17）计算出特征空间上的核局部类间散度矩阵[Kb]，式（18）计算核混合散度矩阵[Kt]。

步骤4 求解特征方程[Kba=λKta]，取前d个最大特征值所对应的特征向量作为最优投影。

步骤5 根据式（20）将特征空间中新的测试样本[?（z）]映射到该最优投影上，根据最近邻分类器分类。

3 实验仿真与分析

为了验证文中提出算法的合理性，在YALE、ORL和AR人脸数据库上进行仿真，将仿真结果和LDA，LPP，LFDA进行对比。实验中，采用高斯核函数[K（X，Y）=exp（-X-Y2/σ）]，（本文[σ=1.5e+8]）。

3.1 实验1与分析

实验1在ORL人脸库上进行实验仿真，ORL人脸库包含400张分辨率为112×92像素的图像（400张图像中包含40个不同的人，每个人10张图像），人脸库中的图像在人脸的面部姿态和表情方面有不同程度的变化。

在进行实验时，选择了每个人的前5张图像作为训练样本，测试样本由剩余的5幅组成。我们比较了四种算法的识别效果，取10次实验的平均值作为仿真结果。图1给出了ORL库中一个人的10张图像，图2中的仿真结果描述了5张图像作为训练样本4种算法的性能比较，表1列出4种算法的最高识别率及相应的投影轴维数。

从图2和表1中可以明显地看出，在五个训练样本情况下，算法KLFDA在最近邻分类器下的识别性能优于LDA，LPP及LFDA。KLFDA算法可以把识别率的值从12.00%提高到90.00%，随着投影轴维数增加，识别率平稳上升，当投影轴维数为47时，该算法可使识别率的值达到90.00%。同时，文中所提出的算法最大识别率达到了90.00%，比另外三种算法的最低识别率高12%、最高识别率高5%。该实验结果说明本文算法在抽取鉴别信息时具有良好的稳定性和鲁棒性。

3.2 实验2与分析

实验2在YALE人脸库上进行实验仿真，YALE人脸库包含165张分辨率为100×80像素的图像（165张图像中包含15个不同的人，每个人11张图像），库中的图像受光照条件下的影响较大，细节（戴或不戴眼镜）和面部表情（惊讶、伤心正常、开心、眨眼等）也有比较显著的差异。

在进行实验仿真时，从人脸库中随机选择每类人脸的5幅图像作为训练样本，剩余的6幅作为测试样本。我們比较了四种算法的识别效果，以10次实验的平均值作为仿真结果。图3给出了YALE人脸库的某一个人的11张图像，图4描述了4种算法的识别率曲线与维数，表2列出了4种算法的最大识别率和相应的投影轴维数。

从图4和表2中很容易看出，本文所提出的算法KLFDA在最近邻分类器下，识别性能远优于另外三种算法。仅当投影轴维数达到14时，该算法可使识别率达到最大值98.89%，且投影轴维数到14以后，逐渐趋于稳定。LDA，LPP和LFDA算法的最高识别率分别为78.89%，94.44%，95.56%，它们取得最高识别率的投影轴维数分别为14，38，18。该实验结果验证了本文算法KLFDA在引入核技巧同时考虑样本在特征空间的局部结构，能够更好地抽取人脸图像的非线性结构，因而具有好的分类和识别性能。

3.3 实验3与分析

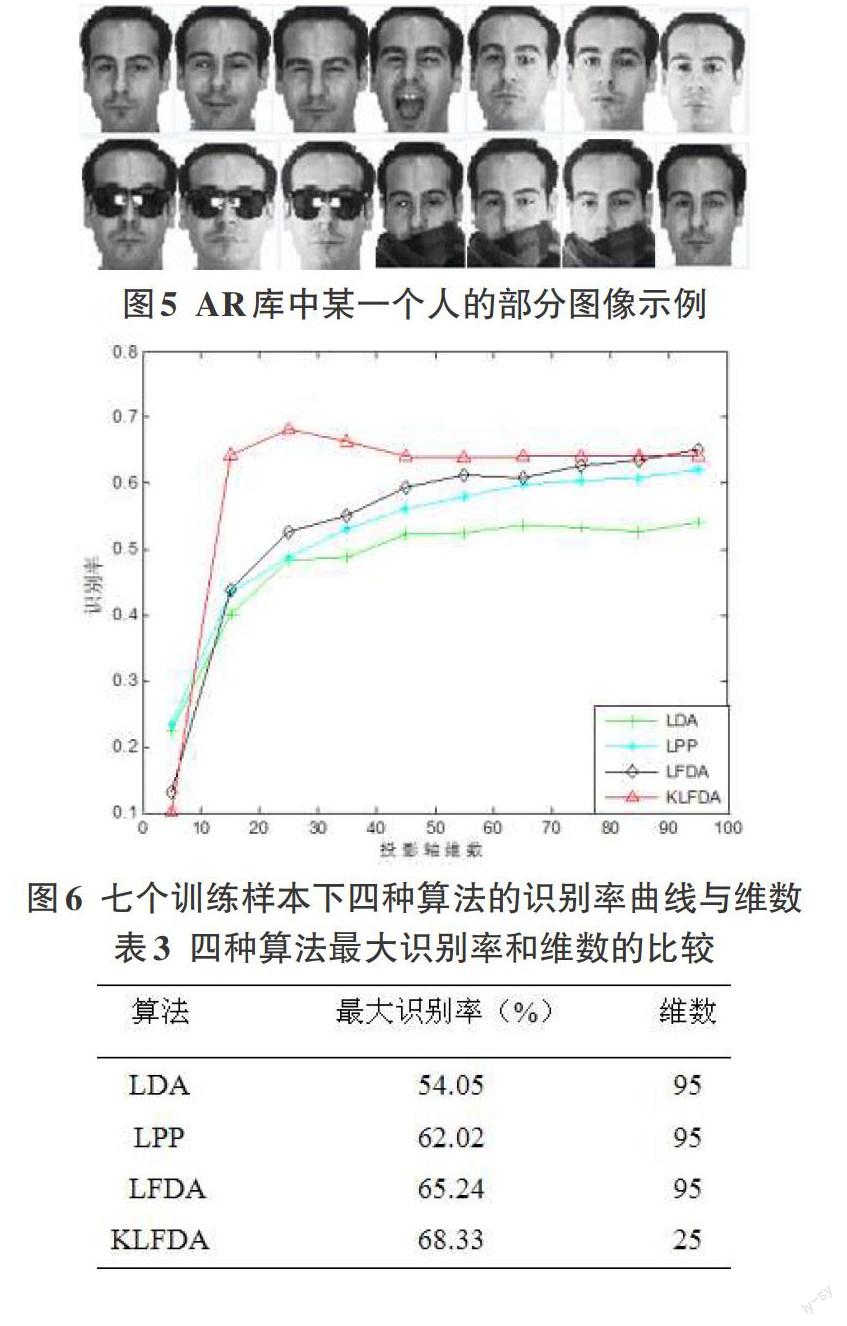
本实验采用AR人脸库，AR人脸库包含3120张分辨率为40×50像素的图像（包含120个不同的人，每个人26张图像），这些图片受光照、表情。姿势以及遮挡的影响。在进行实验仿真时，选择前7幅图像（没有遮挡，只有表情变化）作为训练样本，剩余的7幅（大部分均为有遮挡）作为测试样本。以10次实验的平均值作为仿真结果。图5给出了AR人脸库中一个人的部分图像示例，图6描述了各种算法的识别率曲线与维数的关系，表3列出了4种算法的最大识别率和相应的维数。

从图6和表3中不难看出，在七个训练样本情况下，本文算法KLFDA的识别性能明显优于另外三种算法。仅当投影轴维数达到25时，识别率最大值达到68.33%，当投影轴维数大于25时，本文算法识别率基本趋于稳定。LDA，LPP和LFDA算法的最高识别率分别为54.05%，62.02%，65.24%，它们取得最高识别率的投影轴维数均达到95。这也说明将维后的特征空间能更好地描述原来的特征空间。

4 结束语

基于核的特征抽取算法能够有效地抽取样本的非线性鉴别信息，本文算法结合了核技术和Fisher判别分析的优点，在特征抽取时一方面能够使比较复杂和非线性的原始数据线性化、简单化，另一方面考虑了数据的局部领域结构，从而能够有效消除数据特征之间的信息冗余。然而，本文所提出的算法是一种有监督的学习方法，如何将其发展为半监督学习，并提高分类和识别性能，这仍然值得探索和研究。

参考文献：

[1] Belhumeur P N. Eigenfaces vs. Fisherfaces： Recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19（7）：711-720.

[2] Zhao W， Chellappa R， Phillips P J， Rosenfeld A. Face recognition ： A literature survey[J].ACM Computing Surveys， 2003，35（4）： 399-458.

[3] Fisher R A. The use of multiple measurements in taxonomic problems[J].Annals of Eugenics，1936，7（2）： 179-188.

[4] Sugiyama M. Local Fisher discriminant analysis for supervised dimensionality reduction[C]// Proceedings of the 23rd International Conference on Machine Learning， Pittsburgh， Pennsylvania， 2006： 905-912.

[5] Sugiyama M， Ide T， Nakajima S， et al. Semi-supervised local Fisher discriminant analysis for dimensionality reduction[J]. Machine Learning， 2008，78（1/2）：35-61.

[6] 許淑华， 齐鸣鸣. 稀疏局部Fisher判别分析[J].计算机工程与应用，2012，48（4）：173-175.

[7] He Xiaofei， Niyogi P. Locality preserving projections [C]//proceedings of the Conference on Advances in Neural Information Processing Systems. Cambridge： MIT Press， 2003： 153-160.

[8] Lu J， Plataniotis K N， Venetsanopoulos A N. Face recognition using kernel direct discriminant analysis algorithms [J]. IEEE Trans Neural Network， 2003，14（1）：117-126.

[9] Yang J， Jin Z， Yang J Y. Essence of kernel Fisher discriminant： KPCA plus LDA [J].Pattern Recognition， 2004，37（10）： 2097-2100.

[10] 高秀梅， 杨静宇， 杨健. 一种最优的核Fisher鉴别分析与人脸识别[J].系统仿真学报，2009，16（12）：2864-2868.

[11] Seung H S， Lee D D. The manifold ways of perception [J]. Science，2000，290（22）：2268-2269.

[12] Bengio Y， Palement J， Vincent P， et al. Out-of-sample extensions for LLE， isomap， MDS， eigenmaps， and spectral clustering [J]. Neural Computation， 2004， 16（10）： 2179-2219.