大规格高强度角钢构件轴压承载力计算方法研究

柯 嘉，吴海洋，徐 彬，高 彬

(中国电力工程顾问集团中南电力设计院，湖北 武汉 430071)

大规格高强度角钢构件轴压承载力计算方法研究

柯 嘉，吴海洋，徐 彬，高 彬

(中国电力工程顾问集团中南电力设计院，湖北 武汉 430071)

大规格高强度角钢构件是指肢宽不小于220 mm、肢厚不小于20 mm，材质为Q420及以上的角钢构件，其在输电线路工程中已开始应用，但对于大角钢构件轴压承载力计算方法尚缺乏深入研究。针对输电线路工程常用的大角钢构件展开试验研究。根据试验结果，提出大角钢构件轴压承载力计算方法，并与国外主要规范计算结果进行比较，结果表明：该计算方法具有较好的可靠性。针对某输电塔，分别按照b类截面、推荐计算方法进行设计，采用推荐计算方法设计时，输电塔重可降低1.8%，具有较好的经济效益。

大规格高强度角钢；轴压承载力；试验；计算方法研究 。

1 概述

大规格高强度角钢构件(以下简称大角钢)是指肢宽不小于220 mm、肢厚不小于20 mm，材质为Q420及以上的角钢构件。大角钢构件近年在特高压输电线路工程中开始广泛应用 ，但是目前对于大角钢构件的设计仍然采用与普通角钢构件相同的设计理论，即按照《钢结构设计规范》(GB 50017—2003)的b类截面计算轴压承载力。

在多个工程的铁塔试验中，按照b类截面设计时，大角钢均表现出较强的超载能力。有试验表明，按照b类截面设计时，按理论计算大角钢构件将在115%的设计荷载作用下破坏。但试验加载到设计荷载的130%时该构件仍未破坏。显然，按照目前的计算方法大角钢构件设计偏于保守。在工程设计中，大角钢构件的高强承载力应得到更为充分的利用，从而节省工程造价。大角钢构件的轴压承载力究竟应如何确定，目前鲜有研究。

本文针对输电线路工程中常用的大角钢构件轴压承载力了展开试验研究，与各国规范进行比较，提出一种合理的大角钢轴压承载力计算方法。

2 试验概括

2.1 试件设计

输电线路工程中，大角钢构件多用于铁塔主材构件，其长细比一般为35～55，其肢宽一般为220 mm、250 mm。因此，用于轴压试验的大角钢试件截面规格、长细比见下表。

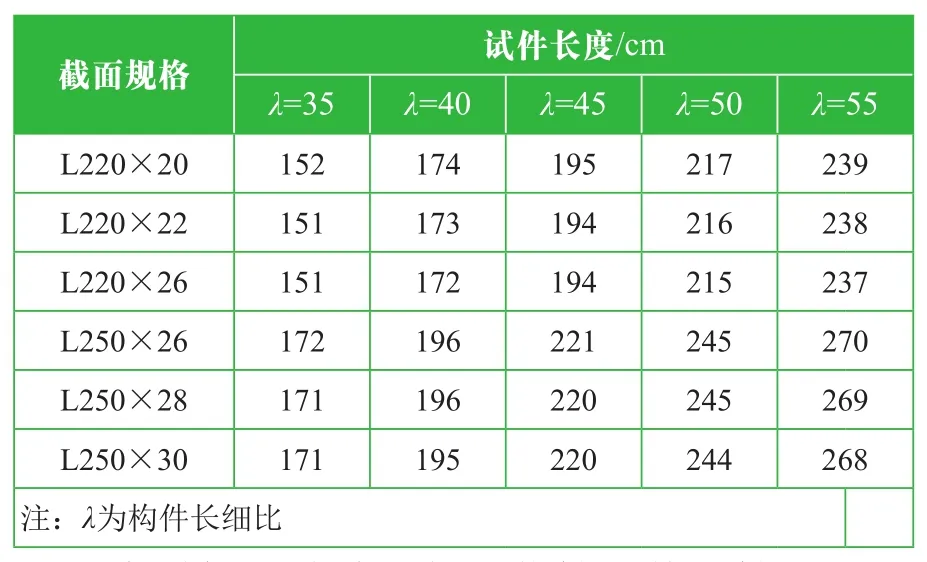
表1 试件的截面规格和长细比

为增加试验结果的可信性和统计性，对同一截面规格、同一长细比，均采用三个相同试件进行试验。本次试验共采用6种截面规格、5种长细比，共90个试件。

2.2 材性试验

对每种截面规格的试件，采用3根标准棒材，进行轴向拉伸，测量其应力－应变关系曲线。共进行了6组18根标准棒材的轴向拉伸材性试验。标准棒材试样加工图见图1。

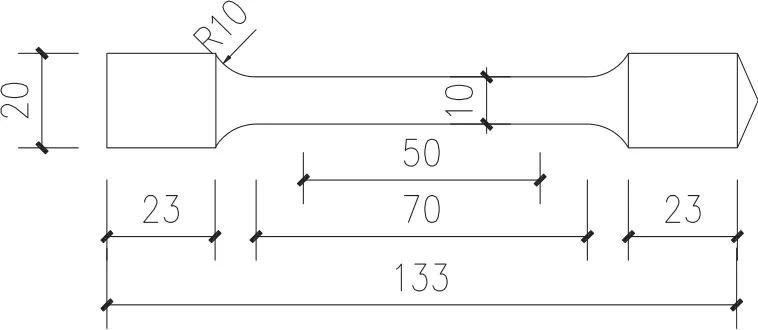
图1 用于材性试验的标准棒材

根据材性试验结果，对于不同截面规格的大角钢试件，其材性并不完全相同。故对每种截面规格的大角钢试件，取不同的屈服强度fy、极限强度fu作为进一步分析的依据。各截面规格大角钢试件的屈服强度fy、极限强度fu见表2。

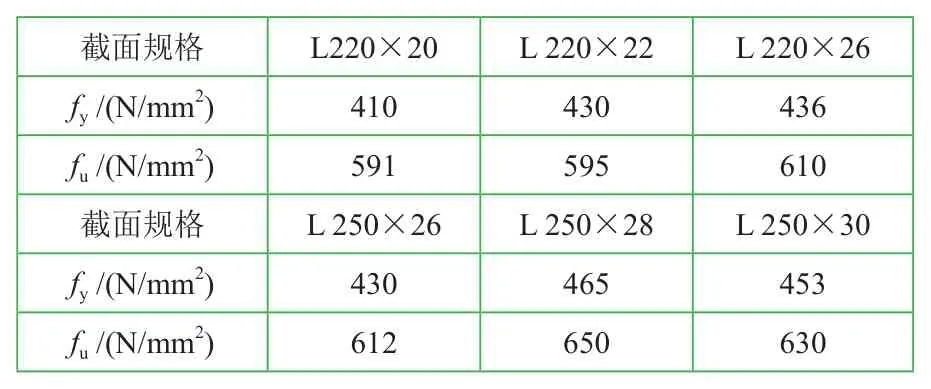
表2 各截面规格的材性试验结果

2.3 加载方案和测量方案

输电铁塔一般为桁架结构，其角钢构件可以按照两端铰接的杆单元进行受力分析。因此，按照“两端铰接”的受力模型设计大角钢构件的加载方案，试件两端采用球绞，加载装置见图2。

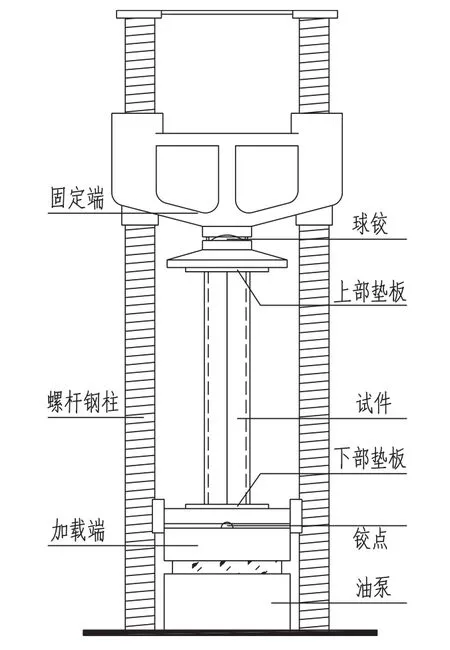
图2 试验加载装置

肢宽为220 mm的大角钢构件采用500 t压力机加载，肢宽为250 mm的大角钢构件试验采用2000 t压力机加载。

本次试验采用静力分级加载的方法进行。对于每一根大角钢试件，在加载前使用有限元软件ANSYS进行数值模拟预估其极限承载力，根据预估极限承载力确定施加荷载的级数和每一级荷载的大小。

本试验的观测内容主要有：

(1)位移观测：观测试件的轴向变形和弯曲变形。在加载机上下端设置竖向位移表，用于观测试件的轴向压缩量；在试件中部设置指向形心的水平位移表，用于观测试件的挠曲幅值，见图3。

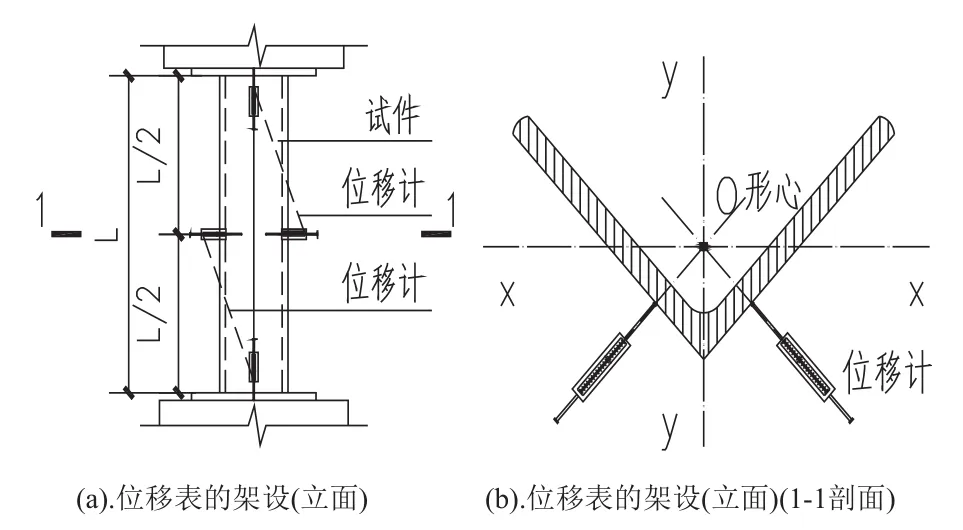
图3 位移测量方案

(2)应变测量：观测试件中部截面应力分布、变化。将应变片沿试件纵轴向，粘贴于试件中部。每根大角钢试件设置6个测点，测点设置于角钢两肢距边缘10 mm处，见图4。

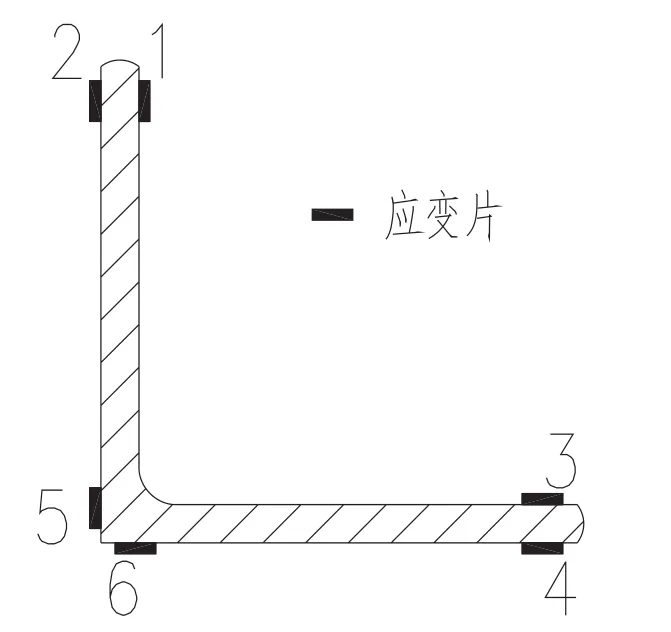
图4 应变测量方案

3 试验结果及分析

3.1 构件破坏特征

在初始加载阶段，试件变形以轴向压缩变形为主。随着荷载的不断加大，试件中部发生弯曲，大部分试件中部的两个位移计均被压缩(或均发生延伸)，即2～5面、4～6面的水平位移方向相同(见图5)，这表明试件向肢背方向(或肢尖方向)弯曲。荷载继续加大，试件弯曲变形持续增加。当荷载达到某个值时，荷载不再加大，试件的弯曲变形仍然在增加，构件变形肉眼可见，这表明构件中部已进入塑性，整个构件发生失稳破坏，失稳形态表现为弯曲失稳。

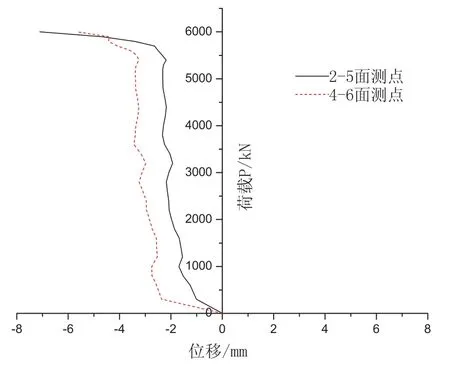
图5 试件中部水平位移测量结果(弯曲失稳)

在加载过程中，少数构件会出现另一种情况，即中部的一个位移计被压缩、另一个位移计则延伸，即2～5面、4～6面的水平位移方向相反(见图6)，这表明试件存在一定的扭转变形。该构件失稳形态表现为弯扭失稳。

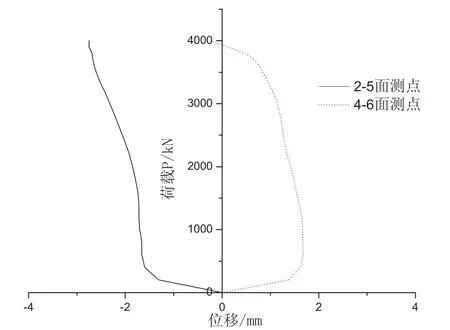
图6 试件中部水平位移测量结果(弯扭失稳)

3.2 构件轴压承载力

根据实测的构件截面积和屈服强度值，按照《钢结构设计规范》(GB 50017—2003)的b类截面计算各试件的轴压承载力，将计算结果与试验得到的构件承载力进行比较。L220×20等试件的轴压承载力比较见图7。

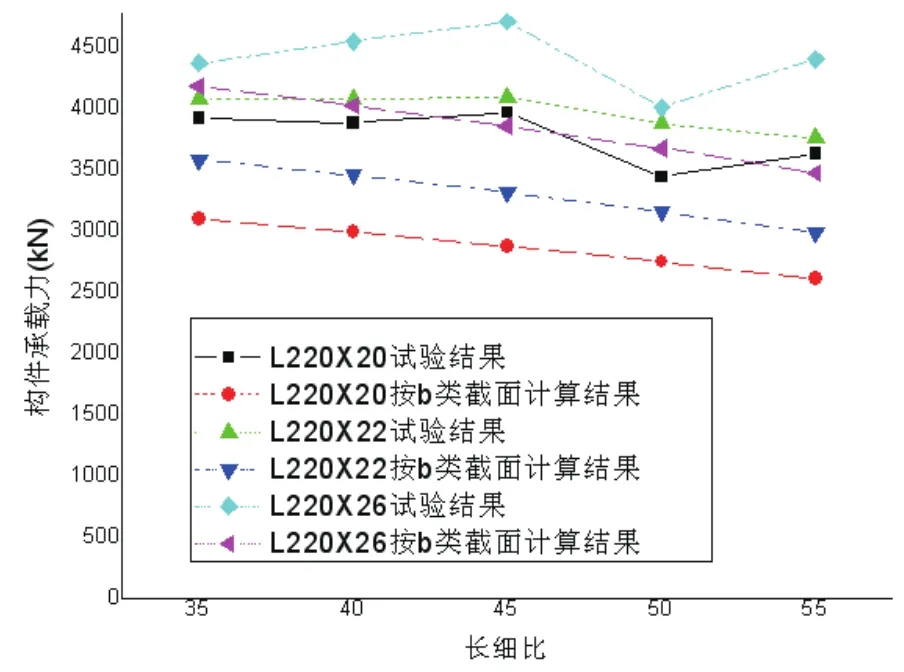
图7 试件轴压承载力比较

从图7看到，对于L220×20截面的试件，按b类截面计算的构件承载力为2600～3100 kN，而其试验结果为3600～4000kN，比b类截面计算结果高20%～30%。对于L220×22、L220×26截面的试件，其试验结果比b类截面计算结果高15%～25%。对于L220×26截面的试件，其试验结果比b类截面计算结果高10%～20%。

可见，按照b类截面计算的大角钢构件承载力明显低于试验值，不能真实反映构件的实际承载力。对L250×26等其他试件展开分析，可以得到类似结论。

由于采用b类截面进行大角钢构件设计偏于保守，需要针对大角钢构件提出一种更为合理的承载力计算方法。

4 大角钢轴压承载力计算方法

4.1 大角钢轴压承载力的推荐计算方法

为结合我国工程实践，本文推荐的大角钢轴压承载力的计算方法，采用与《钢结构设计规范》(GB 50017—2003)相同的计算形式，即：

实腹式大角钢压杆设计承载力N应满足：

式中：A为实腹式大角钢压杆总截面面积；f为

大角钢压杆钢材屈服强度设计值；φ为轴

心受压构件的稳定系数。大角钢压杆稳定系数φ按下式确定。

当λn≤0.215时：

当时：

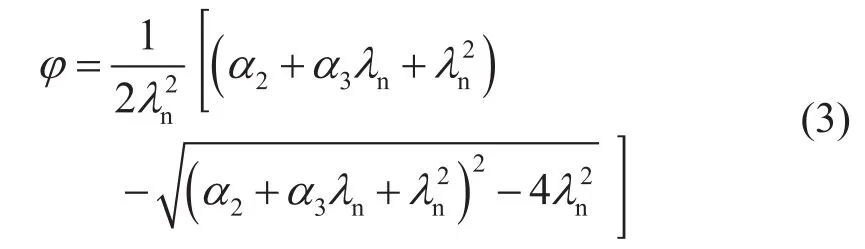
式中：λn为正则化长细比，

根据本文的试验结果，通过实测数据对计算参数α1、α2和α3进行非线性拟合分析，确定其取值，见表3。

表3 系数取值

利用推荐计算公式，绘制出相应的柱子曲线，并与现行规范中的四类柱子曲线进行对比，见图8。

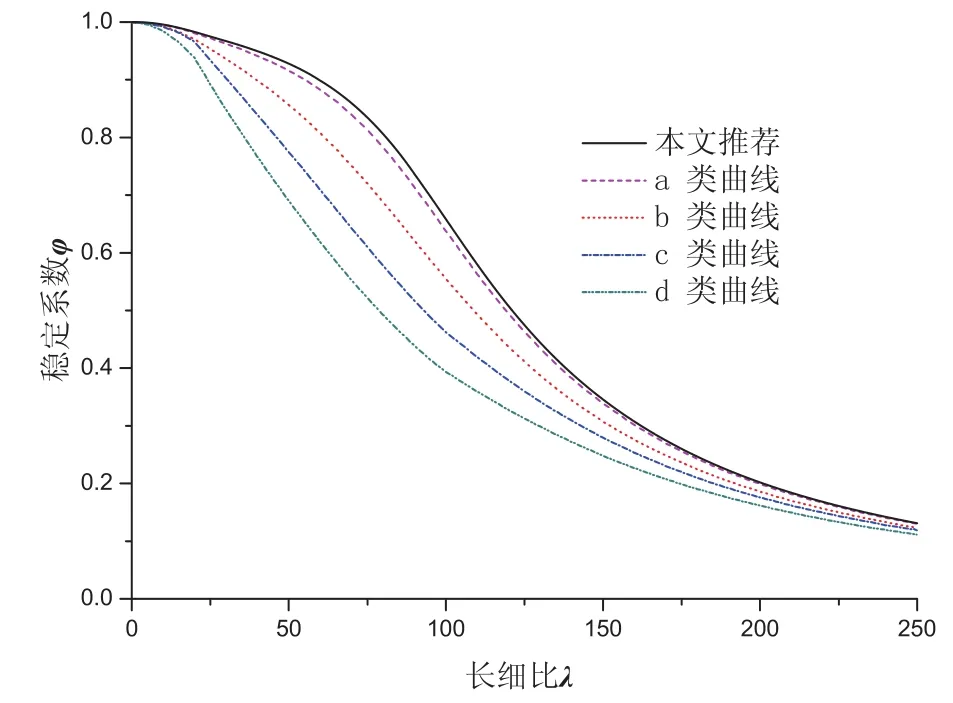
图8 大角钢轴压构件推荐的柱子曲线

从图8可以看到，推荐计算方法的稳定系数明显高于b类截面取值，与a类截面取值基本相当。

4.2 推荐计算方法的评价

为更好的评价推荐公式的可靠性，针对试验研究涉及的所有截面规格、所有长细比的构件，分别按照我国规范(GB 50017—2003、DL/T 5154—2010) 的a、b类截面，美国规范(ASCE10—97、AISC—2000)，欧洲规范(Eurocode:3)，澳大利亚规范(AS4100—1998)等国内外主要规范进行大角钢构件轴压承载力计算。为方便比较，将构件承载力进行无量纲化，即对稳定系数展开比较。

推荐公式、试验结果、各规范计算得到的稳定系数进行了比较见图9。

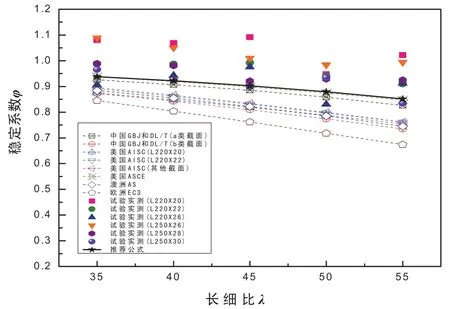
图9 推荐公式、试验结果、各规范计算的稳定系数比较

从图9可以看到：

(1)长细比35～55范围内，推荐公式给出的稳定系数基本低于试验结果，具有95%的保证率，说明推荐公式具有较好的可靠性。

(2)长细比35～55范围内，推荐公式和我国规范(GB20017、DL/T 5154)的a类截面、美国规范(ASCE、AISC)、澳大利亚规范(AS4100)计算的稳定系数较为接近，均高于b类截面设计结果。ASCE等规范的计算结果进一步印证了推荐公式的可靠性。

(3)目前，输电线路工程采用的大角钢构件多用于铁塔主材，长细比集中于35～55范围内。因而，推荐公式可以较好地应用于输电线路工程设计。

综上所述，大角钢受力性能好，甚至优于我国规范a截面，采用推荐公式可以更真实的反映大角钢的承载能力。从试验结果、国内外规范比较来看，在长细比35～55范围内，推荐公式具有较好的可靠性，可较好地应用于输电线路工程设计。

5 技术经济分析

针对某特高压输电线路工程塔型JC31152，分别按照b类截面、推荐计算方法进行设计。计算结果表明，与b类截面设计相比，采用推荐计算方法时，同样部位的大角钢构件规格能降低一级，见表4。

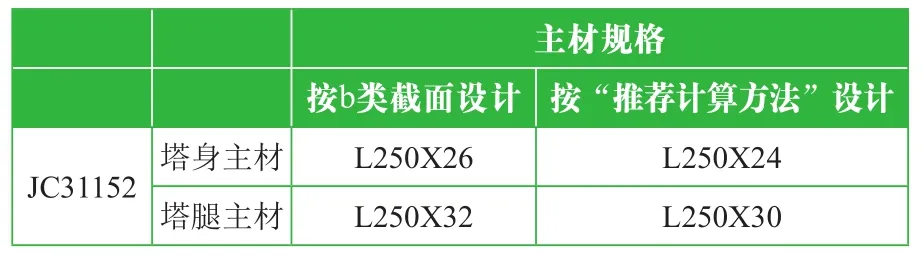
表4 按不同方式设计时，典型塔的主材规格对比

采用不同设计方法时，JC31152的塔重比较见表5。

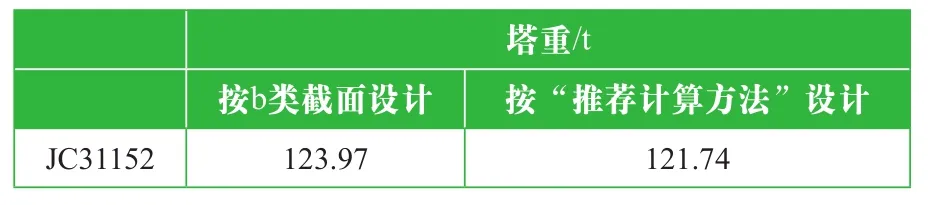
表5 按不同方式设计得到的典型塔塔重

由于特高压输电线路铁塔荷载较大，大角钢构件使用量大，采用推荐计算方法设计时能够较大幅度的降低塔材指标。初步计算和统计结果表明：采用推荐计算方法设计时，JC31152塔重可降低1.8%，具有较好的经济效益。

6 结论

针对输电线路工程中常用截面规格和长细比的90根试件，展开大角钢轴压承载力试验研究，提出大角钢轴压承载力的推荐计算公式，并与各国规范进行比较，得到以下结论：

(1) 轴压试验表明，大角钢构件失稳模态一般表现为弯曲失稳，少数构件表现为弯扭失稳。

(2) 轴压试验表明，大角钢构件的轴压实际承载力明显高于b类截面(《钢结构设计规范》(GB50017－2003))计算值，按b类截面设计偏于保守。

(3) 提出了一种大角钢构件轴压承载力的计算方法。将推荐计算方法与试验结果、ASCE等国内外主要规范的计算结果进行比较表明，推荐计算方法具有较好的可靠性。

(4) 针对某特高压输电线路工程塔型JC31152，分别按照b类截面、推荐计算方法进行设计。计算结果表明：采用推荐计算方法设计时，JC31152塔重可降低1.8%，具有较好的经济效益。

[1] 李茂华． 输电杆塔结构用材料最新进展[J]． 武汉大学学报(工学版)， 2011，44．

[2] 杜荣忠．Q420大截面角钢在特高压输电线路中的应用[J]．电网与清洁能源， 2011，27(11)．

[3] 黄璜．Q420大规格角钢在±800 kV 特高压杆塔中的应用[J]．电力建设，2010，31(6)．

[4] 刘泽洪． 大规格角钢在输电铁塔中的应用[M]．北京：中国电力出版社，2011．

[5] GB/T 228.1—2010 金属材料拉伸试验第一部分:室温试验方法[S]．

[6] 陈骥． 钢结构稳定理论与设计3版[M]． 北京：科学出版社，2006．

[7] GB 50017—2003，钢结构设计规范[S]．

[8] DL/T 5154—2012，架空送电线路杆塔结构设计技术规定[S]．

即使在最糟糕的情况下，即基线长度在300 km的时候，坐标改正误差也在0.6 mm以内，因此由于基准不一致而引起的误差可以完全忽略不计。

4 结论

根据这篇文章的相关讨论，可以知道，在进行载波相位差分定位中，当流动站与基准站间距离一定时，由于轨道误差而引起的差分误差改正将随着轨道误差的增大而线性增大；当轨道误差一定时，差分误差改正项将随着流动站之间的距离的增大而线性增大。

基于文章的分析，可以得到一个重要的结论：无论精度要求多高，由于基准不一致所带来的影响完全处在可以忽略的水平。当使用精密星历时的定位精度并不是本文所关心的问题。在RTK中，还使用了一些其他的方法对各种误差进行削弱和消除，因此，当使用广播星历或精密星历，且基准坐标为CGCS2000时，由于基准不一致而引起的误差可以完全忽略。 同时也可以得到另外一个结论，即由于基准(CGCS2000，IITRF 和WGS84)引起的误差对于任何基于差分定位的定位方法均可以忽略不计。

参考文献：

[1] 陈俊勇．大地坐标框架理论和实践的进展[J]．大地测量与地球动力学，2007，(01)．

[2] 陈俊勇．中国现代大地基准—中国大地坐标系统2000(CGCS200)及其框架[J]．测绘学报，2008，(03)．

[3] 成英燕，等．基于现框架下的省市CORS站到CGCS2000的转换[J]．测绘学报，2001，(07)．

[4] 程鹏飞，等．2000国家大地坐标系椭球参数与GRS80和WGS84的比较[J]．测绘学报，2009，(03)．

[5] 吴北平．GPS网络RTK定位原理与数学模型研究[C]．2003．

[6] 魏子卿．关于2000中国大地坐标系的建议[J]．大地测量与地球动力学，2006，(02)．

[7] 于强，易长荣，占惠．ITRF2000转换到CGCS2000框架的分析[J]．全球定位系统，2009，(05)．

[8 李征航，黄劲松．GPS测量与数据处理[M]．武汉大学出版社，2005．

[9] 郭兴，施昆．GPS网络RTK误差改正数生成算法精度分析[J]．江西科学，2010，(05)．

[10] 卫柳燕．GPS网络RTK系统的算法及定位精度研究[C]，2006．

[11] 焦海松，王红芳，姚飞娟．卫星星历误差对GPS定位精度的影响分析[J]．全球定位系统，2009，(01)．

Study on Calculation of Axial Compressive Bearing Capacity of Large-section and High-strength Angle Members

KE Jia, WU Hai-yang, XYU Bing, GAO Bing
( Central Southern China Electric Power Design Institute of China Power Engineering Consulting Group Corporation, Wuhan 430071, China)

Large-section and high-strength angle steels are construction members with limb width larger than or equal to 220mm, limb thickness larger than or equal to 20mm, and strength higher than or equa1 to Q420. Such kind of members have begun to be used in the field of steel transmission towers. However the calculating method of axial bearing capacity for the members lacks further research. The axial compression column tests were conducted for the large-section and high-strength angle steels. Based on the test results, the calculating method of axial bearing capacity was put forward and coMPared with column curves from different foreign codes. It is shown that this calculating method has good reliability. Concretely to some transmission tower, according to the section B and commendatory calculating method adopted in this paper, the weight of the transmission tower could decrease 1.8% and has good economic benefits.

large-section and high-strength angle; axial compressive bearing capacity; experimental; study on calculation.

TM75

B

1671-9913(2015)05-0053-05

2015-04-15

柯嘉(1985- )，男，湖北黄冈人，工学硕士，从事输电线路结构设计研究工作。

国家自然科学基金(51378401)，中国电力工程顾问集团中南电力设计院科技项目(40－1A－KY201219－T01)。