面元法中偶极子影响系数计算分析*

李洪涛 杨 勇

(1.海军工程大学训练部 武汉 430033)(2.驻上海江南造船(集团)有限公司军事代表室 上海 201913)



面元法中偶极子影响系数计算分析*

李洪涛1杨 勇2

(1.海军工程大学训练部 武汉 430033)(2.驻上海江南造船(集团)有限公司军事代表室 上海 201913)

分析了不同方法应用于偶极子影响系数的计算,并详细介绍了Gauss-Bonnet定理在偶极子影响系数计算中的应用。探讨了这些计算方法的近似处理及由此造成的误差,进而以Gauss-Bonnet定理为基础提出了计算偶极子影响系数的修改办法。将此种修改办法应用于面元法的计算中,以×××桨及×××桨为计算对象,分析修改前后的偶极子计算方法对计算结果精度的影响。从理论上探讨了面元法中,有关偶极子影响系数计算环节的误差及减小此部分误差的办法。

面元法; 偶极子; 影响系数; Gauss-Bonnet定理

Class Number TP206

1 引言

面元法以其准确的数学和物理模型,较快的计算速度和较高的计算精度,已广泛应用于螺旋桨的水动力性能预报。目前主要有基于速度和基于速度势的两种面元法。以速度势面元法为例介绍面元法的基本原理,其主要是利用格林公式和拉普拉斯方程基本解的存在,将物面和尾涡面以某种规律划分成小面元,在小面元上布置等强度源汇及偶极子,这一过程中以现阶段比较普遍的面元划分方法为例,即划分成双曲四边形面元。以控制点在场点产生的扰动速度势和流体在物面上法向速度为零的条件建立起离散后针对小面元积分的方程。而这个离散的积分方程每一离散项中,仅与物面以及尾涡面几何形状有关的系数即被称之为影响系数,因此在面元法计算分析过程中影响系数的计算表达是比较重要的环节。到目前为止,计算影响系数主要有两种方法,一种是Morino[1～2]在1974年、1975年发展的一套影响系数计算方法,另一种是Newman[3]在1986年提出来的关于以立体角概念计算的方法。两种计算方法在最终的表达形式上没有太大区别,同样两种方法都有各自的近似成分。在这里主要对偶极子影响系数的计算表达作详细的讨论分析。

2 不同方法计算影响系数时的原理分析

2.1 应用积分原函数法计算偶极子影响系数

偶极子影响系数可表达为式(1)。

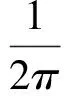
(1)

此类方法是由Morino发展的一套影响系数计算方法,基本原理是通过坐标变换将总体坐标中的双曲四边形面元对应局部坐标的正方形面元,从而在求解的过程中,通过坐标之间的向量关系,运用积分的基本理论求解得到。在这里,称它为积分原函数法,是由于影响系数表达式在变换后,可改写为式(2),求解此式时,以类似于原函数的项表达最终结果。

(2)

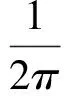
-F(-1,1)+F(-1,-1)

(3)

而其中F(1,1),F(1,-1),F(-1,1),F(-1,-1)的表达式可表示为有关面元法向、切向以及场点到控制点向径的关系式。具体表达见式(4):

(4)

在式(4)中向量R为控制点到场点的向径,向量t1、t2为面元切向。

在上述对偶极子影响系数推导过程中,以解析的式子对偶极子影响系数进行表达。对于式(3)可以从二维泰勒公式展开的角度进行说明(展开到二阶即可),因此对于式(3)要满足的条件即所积分的面元应尽量光滑。就螺旋桨表面而言,在面元较小的情况下,这一条件可以近似满足,但同时要注意,式(3)忽略了高阶的泰勒展开项。

2.2 应用立体角概念计算偶极子影响系数

立体角的概念应用于影响系数的计算是由Newman[3]提出的。主要原理下面将进行分析,对于偶极子影响系数表达式(1)经过简单的数学变换可以表示为式(5)的形式。

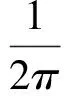
(5)

在对上式处理时,以场点为球心作一个单位球面,那么变形后的表达式可以认为是离散的面元dS在此单位球面上的投影,但要注意到在这里对于投影面元上每一位置处带有cos(n,R)的符号。在符号全相同的情况下可以认为影响系数近似表达为立体角。若是这样的话,对于离散的面元为双曲四边形面元时,根据立体角的计算表达式,影响系数可表达为式(6):

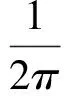
(6)

式(6)中Ii为面元的各个角点的外角,且Ii是带有相同符号的,关于Ii的表达式与运用积分原函数解法中的表达式类似,即式(4)。在实际应用过程中也有用反余弦表示的。但要注意到,满足式(6)的立体角计算中,面元的边应是过大圆的(大圆即是过球心的圆)圆弧,在离散面元较小的情况下,可近似认为这是可以满足的。对于各个角点符号不同时的情况,如上述分析,此时不能直接应用立体角计算公式,这时的处理,在文献[4]中有较详细的讨论。具体方法是,在有一个面元角点符号与其他不同时采用式(7)。

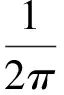
·sgn(I2)+π·sgn(I4)

(7)

在有两个角点符号与其他两个角点符号不同时也采用式(7)。

按照立体角的计算方法,在离散面元的边界不是过大圆弧和离散面元的四个角点符号不全相同,这两种情况下,就只能采取了近似的处理方法,这要求在面元的划分过程中要把握好划分的函数形式,确保较少的面元出现上述情况,并且面元的边界在一定范围内,可近似认为是过大圆弧的。

2.3 应用Gauss-Bonnet定理计算偶极子影响系数

Newman采用立体角计算影响系数时,曾在文献[3]中提到过Gauss-Bonnet定理,但未作详细说明,在这里首先详细说明Gauss-Bonnet定理。Gauss-Bonnet定理是微分几何中关于测地曲率、高斯曲率及曲面内角关系的定理,其数学表达形式为式(8):

(8)

式中Ω是曲面上的单连通区域;n为曲面面元边界线条数;L为组成Ω区域的分段光滑的闭曲线;αi为面元的第i个顶点的内角;K为曲面的高斯曲率;kg为边界曲线L的测地曲率。

当测地曲率kg=0(此时组成Ω区域的分段光滑的闭曲线L均为测地线),高斯曲率K=1时,上式变为式(9):

(9)

式(9)的意义为:在测地曲率恒为0,高斯曲率恒为常数1的情况下,曲面上由式(9)各参数构成的单连通区域Ω的面积等于曲面面元的各顶点内角和减去(n-2)π。

对影响系数式(5)进行分析,前面的处理与立体角法相似,即以场点为球心作一单位球面,则影响系数表达式为面积dS在以场点为球心的单位球面上的投影面积。由于dS是投影到以场点为球心的单位球面上,一方面由几何关系可知,在近似认为面元较小的情况下,投影到单位球面上面元的各条边均是过单位球球心的大圆弧。由微分几何学的相关知识得到,球面上的所有测地线就是过球心的大圆弧的全体(可用数学方法证明),因而投影到单位球面的面元的各条边测地曲率kg恒为0。另一方面,由于面元是投影到单位球面上,故曲面面元的高斯曲率K恒为常数1。综合这两方面的分析可知影响系数的表达式很好地符合了Gauss-Bonnet定理简化后的表达式(9)的计算要求,因此可利用Gauss-Bonnet定理简化式(9)来计算偶极子的影响系数。但同时需要注意到影响系数表达式中由于cos(n,R)并不恒为正,在计算时同样需考虑到其符号变化。

由上述分析可知,Gauss-Bonnet定理的计算方法与立体角的计算方法在本质上是相同的,不同的是Gauss-Bonnet定理从更基础的数学角度,推导出了投影面元面积的计算公式,从而解释了为什么只有投影的面元边线过大圆弧时,才能保证计算公式的准确性。

3 面元角点符号不同时的处理

由前面的讨论可知,在求解偶极子影响系数时,若面元角点符号均相同时,运用立体角方法或Gauss-Bonnet定理是没有太大问题的,而实际计算中会遇到面元角点符号不同的情况,这在文献[4]中讨论过其计算处理方法。但在这里,根据上述理论的推导,相对于文献[4]中的处理,主要针对面元角点有一个符号与其他符号不同时作一些修改。处理方法如下。

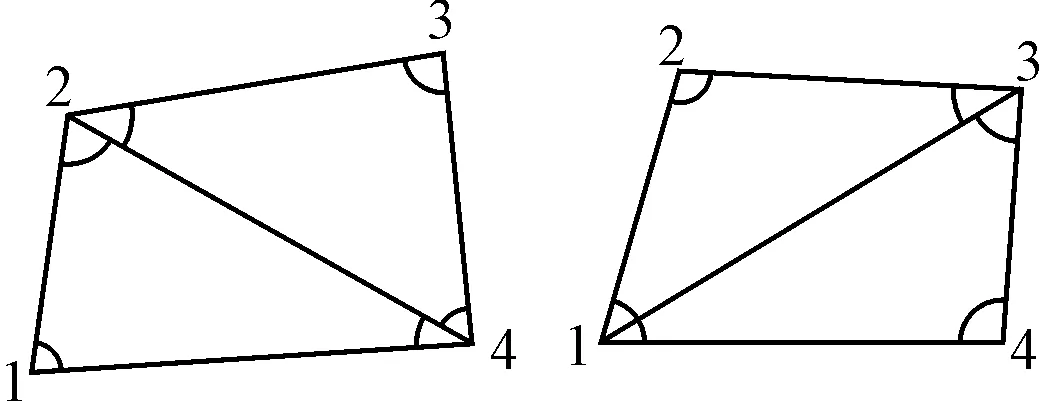
图1 面元修改图

投影面元四个角点的符号有一个与其他角点符号不同时,若沿用式(9)则会不合理。但注意到,由于离散面元在较小的局部范围内,若有一个角点符号与其他三个不同,则三个相同符号所组成的三角面元的角点符号仍可认为是相同的。此时处理方法如图1所示。

当角点1(或角点3)与其他角点的符号不同时,如图1中左图所示,此时将四边形面元分为两个三角形面元,在这两个三角形面元中,由2、3、4三个角点所构成三角形面元的角点符号可近似认为是相同的,因此可直接应用Gauss-Bonnet公式,其表达式为式(10)所示(式中αi不带符号):

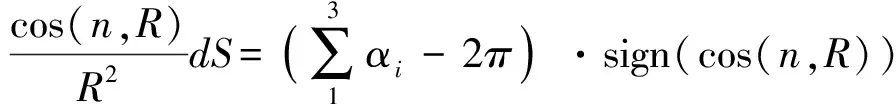
(10)

而另一个三角形面元的表达式则按照近似处理办法,在文献[4]有较详细的说明,其表达式为(式中αi带有符号):

(11)

同理对于角点2(或角点4)与其他面元角点符号不同时,运用与式(10)、式(11)相同的处理办法。相对于对四边形面元作整个的处理,上述的处理方法,保证了面元一部分的偶极子影响系数的计算结果在理论上期的准确度有所提高。

对于有两个角点的符号与其他角点符号不同时,运用了与文献[4]中计算偶极子影响系数相同的处理办法,即与式(7)相同的处理办法。

以上的计算处理,与文献[4]中主要的不同在于面元有一个角点符号与其他角点符号不同时,更精细地处理了偶极子影响系数的计算。从理论上,这样处理后能够提高偶极子影响系数理论上的计算精度。

下面通过将此种修改之后的处理方法应用于×××桨、×××桨敞水性能计算,与修改前的计算结果进行对比,检验此种方法的计算精度。具体对比结果如图2、图3所示。在所有的曲线图中,1为应用修改后方法的计算值,2为原计算值,3为试验值。

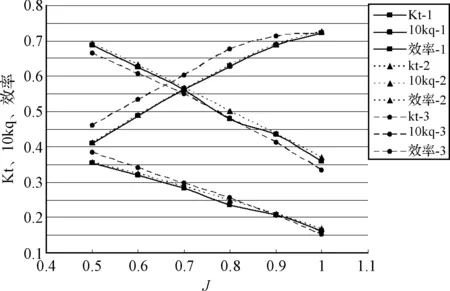
图2 ×××敞水性能比较曲线图

图3 ×××敞水性能比较曲线图

以上对×××桨和×××桨应用修改后的方法求解的结果在某些方面更接近试验值,×××桨运用修改后的计算方法所得到的结果与修改前的计算结果差别不是很大,但在设计点附近,修改后的计算结果要更接近试验值。,×××桨运用修改后的计算方法所得到的计算结果,在Kq的计算上明显要比修改前的计算结果更接近实验值,同样在设计点附近,所得到的计算结果也是优于修改前的计算结果的。但注意到,对于Kt的计算值,修改后的计算结果并不比修改前的计算结果好,而敞水效率的计算结果也没有太大变化。初步分析,由于面元法是在离散的基础上求解迭代的,理论上,网格划分得越密,从几何上看就越接近真实,但同时注意到,离散得越密,以公式计算及向量描述的累积误差则越大。因此合理的划分网格,同时尽量保证面元投影到单位球面上的边界线与过球心的大圆弧重合,对于运用Gauss-Bonnet公式求解时的精度控制有着较大的意义,出现上述计算结果的误差也是两者的综合作用。因此如何选择合适的网格划分,对于此类计算影响系数的方法的应用具有很重要的意义,这也是需要进一步分析的问题。

4 结语

总结了不同方法计算偶极子影响系数,并简要分析了这些计算方法中近似处理。详细介绍了Gauss-Bonnet定理,从微分几何学的角度,更本质地揭露了偶极子影响系数计算的实质,因此对于分析计算中,由偶极子影响系数计算过程产生的误差,能够更深刻的把握,从而为提高这一部分的计算精度作了有益的探索。通过理论分析,提出了计算影响系数修改的方法,从理论上说明了其可行性,并通过对×××桨、×××桨对比计算,详细分析了结果差异的原因,从而揭示出了面元法的计算过程中偶极子影响系数环节的误差来源,进一步明确了面元法在应用过程中有关偶极子影响系数计算方面需要注意的问题。

[1] Morino L, Ching-Ching Kuo. Subsonic Potential Aerodynamics for Complex Configurations: A General Theory[J]. AIAA Journal,1974,12(2):191-197.

[2] Morino L, Chen L, Suciu E O. Steady and oscillatory Subsonic and Supersonic Aerodynamics around complex Configurations[J]. AIAA Journal,1975,13(3):368-374.

[3] Newman J N. Distribution of sources and normal dipoles over a quadrilateral panel[J]. Journal of Engineering Mathematics,1986,120:113-126.

[4] 谭廷寿.非均匀流场中螺旋桨性能预报和理论设计研究[D].武汉:武汉理工大学,2003.

[5] 胡健.螺旋桨空泡性能及低噪声螺旋桨设计研究[D].哈尔滨:哈尔滨工程大学,2006.

[6] 王国强,董世汤.船舶螺旋桨理论与应用[M].哈尔滨:哈尔滨工程大学出版社,2007.

[7] 徐国良.计算几何中的几何偏微分方程方法[M].北京:科学出版社,2010.

[8] 蒋志超,王国强,等.导管面元网格划分和影响系数计算的研究[J].船舶力学,2000,4(5):1-8.

[9] Hess J L. Calculation of Potential Flow about Arbitrary Tree Dimensional Lifting Bodies[R]. Technical Report MDC J5679-01, McDonnel Douglas, Oct 1973.

[10] Kinnas S A, Hsin C Y, Keenan D A. Potential Based Panel Method for the Unsteady Flow Around Open and Ducted Propellers[C]//The 18thSymposium on Naval Hydrodynamics,1991.

Calculation and Analysis of Dipole Influence Coefficient in Surface Panel Method

LI Hongtao1YANG Yong2

(1. Administrative Office of Training, Naval University of Engineering, Wuhan 430033)(2. Navy Representative Office in Shanghai Jiangnan Shipyard(Group) Co., Ltd, Shanghai 201913)

Different methods used in the calculation of dipole influence coefficient were analyzed and the Gauss-Bonnet theory was introduced in detail. The approximate treatment applied to these methods was discussed and the error result from the treatment was analyzed. Then a modified calculation about dipole influence coefficient based on Gauss-Bonnet theory was proposed. The modified method was used in surface panel method, and the propellers DTMB××× and DTMB××× were analyzed by the surface panel method. The result was compared to the calculation without modification. In the end, the error induced by the calculation of dipole influence coefficient was discussed.

surface panel method, dipole, influence coefficient, Gauss-Bonnet theory

2014年9月14日,

2014年11月3日

李洪涛,男,工程师,研究方向:装备综合保障。

TP206

10.3969/j.issn1672-9730.2015.03.011