一种后向安全的混合代理多重签名方案

万世昌

（商洛学院数学与计算机应用学院，陕西商洛726000）

一种后向安全的混合代理多重签名方案

万世昌

（商洛学院数学与计算机应用学院，陕西商洛726000）

以一个随机数为种子，连续做散列运算，计算中生成的有序散列值就构成了一条单向散列链。将单向散列链引入代理签名方案中，设计了一个混合代理多重签名方案。新方案中当前时段的散列值参加签名运算并在验证阶段得到验证，保证了方案的后向安全性，如果当前时段密钥丢失，今后时段签名也不会被假冒。最后分析了方案的安全性和效率。

单向散列链；代理签名；混合代理多重签名；后向安全性

数字签名是利用公钥技术产生的一种类似于物理签名的电子文档。由于数字签名中包含了签名人的身份，所以能够在网络交易中认证签名人并且防止签名人抵赖。Rivest[1]提出第一个数字签名方案后，大量的数字签名方案不断被提出。在某些情况下签名人可能不在现场，必须委托别人进行签名，为了适应这种情况Mambo等[2]提出了代理签名。在代理签名机制中，原始签名人可以指定一个代理人代理自己签名。随后代理签名受到广大研究者的关注，并把这种机制进行了细化研究，提出了在不同场合使用的代理签名体制，如代理盲签名、代理环签名、代理多重签名[3-8]等签名体制。在一个代理多重签名方案中，指定的一个代理人代表多个原始签名人进行签名。但是如果有部分原始签名人刚好在场他可以自己完成签名，而其余的原始签名人委托代理人进行签名，适应这种特殊情况的签名称为混合代理多重签名。随后出现了很多混合代理多重签名方案，如文献[9-10]，在这些方案中，如果当前秘钥泄露，已有的签名将不再安全。Anderson[11]首次提出前向安全的概念，文献[12]在文献[10]基础上将前向安全概念应用到混合代理多重签名方案中，提出一个前向安全的混合代理多重签名方案，但是该方案并没有实现后向的安全性。何滨等[13]提出了一个前向安全的无证书代理盲签名方案，利用单向散列链解决了签名的后向安全性。本文将单向散列链引入混合代理多重签名方案中，设计了一个混合代理多重签名方案。新方案既有原方案的前向安全性又增加了后向安全性，如果当前时段密钥丢失，今后时段签名也不会被假冒。最后对安全性和效率做了分析。

1 相关知识

1.1 双线性对

假设由生成元p生成的阶为q的循环加法群为G1(其中q为素数)，阶为q的循环乘法群为G2；并假定在这两个群中解决DL问题是困难的。那么一个映射e:G1×G1→G2称为双线性对，其具有的性质为：

1)对于∀P，Q，R∈G1以及∀a，以下等式成立：

2)对于∀P，Q∈G1有e(P，Q)=e(Q，P)-1。

3)在群G1中∃P∈G1使得e(P，P)≠1。

4)对于P，Q∈G1，一定有确定的算法计算e(P，Q)。

下面是群G1中的几个问题：

3)如果群G1中判定问题是容易的，计算问题是难解的，那么就称群G1为GDH群。

1.2 单向散列链

随机选取a作为散列链的初始值,通过将单向散列函数H(·)进行递归运算Hk(a)=H(Hk-1(a))得到一组散列值序列a，H(a)，H2(a)，…，Hk(a)，…，HT(a)，其中参数(k＝1，2，…，T；H0(a)=a)，就称这组散列值序列为长度为T，初始值为a的单向散列链。其满足以下性质：

1)知道Hk(a)但没有获得值a,无法计算出Hk-1(a)。

2)通过Hk(a)可以验证Hk-1(a)的正确性,即计算H(Hk-1(a))=Hk(a)若等式成立说明Hk-1(a)是正确的。

2 签名描述

2.1 系统参数

假设由生成元p生成的阶为q的循环加法群为G1（其中为q安全的大素数），阶为q的循环乘法群为G2，双线性对e:G1×G1→G2是G1×G1到G2的一个双线性的映射，另外定义三个安全的Hash函数H1:{0，1}*→G1，，。将以下系统参数(G1，G2，e，q，p，H1，H2，H3)公开。本签名方案的参与者有l个原始签名人，私钥为，(0≤i≤l)，公钥是PAi=xAiP；一个代理签名人B，其私钥为xB，公钥是PB。在全部的原始签名人中假设Ai(0≤i≤l1)个需要代理人代理自己签名，剩余的原始签名人Aj(l1＜j≤l1＋l2=l)自己参与签名。原始签名人Ai指定一个合理的时间段1，2，…，T，将原始签名人Ai(0≤i≤l1)给代理签名人B的委托授权记为wi(0≤i≤l1)，wi内容涵盖Ai、B的身份、权限以及代理权的有效期限等。

2.2 签名权委托

Ai(0≤i≤l1)生成随机数，计算等式:

则Ri=riP，Ri，wi为公共参数，然后把SAi传递给B，B收到SAi后，计算下列等式是否成立：

如果等式成立，那么B认为Ai委托有效，等式不成立则认为Ai的委托无效，或者告诉Ai重发SAi。

2.3 生成代理密钥

令xB，0=xB，则代理签名人B初始密钥为：

代理签名人B根据S0计算出公共参数，记，当一个时间段变为k(0＜k≤T)时，B通过k-1时间段的私钥xB，k-1算出当前时间段私钥xB，k以及当前时间段的签名密钥Sk:

代理签名人B把时间段更新为下一时间段，为了保证安全性，销毁xB，k-1和Sk-1。生成一个随机数，将其作为散列链的初始值并保密存放。计算z0=H3T(a)，销毁计算中的临时值并公开z0，将其用于后向安全验证。

2.4 签名完成

1)原始签名人Aj(l1＜j≤l1＋l2)参与消息M的签名，生成随机数，并计算：

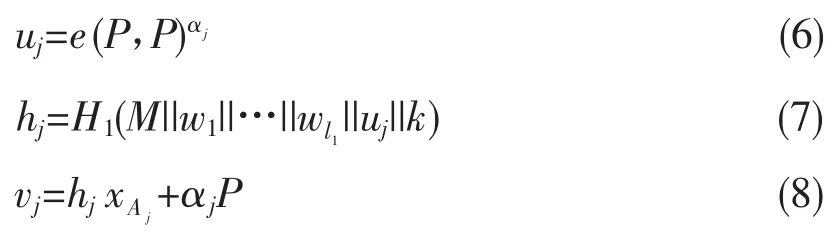
公开(uj，vj)。

2)代理签名人B参与消息M的签名，生成两个连续的散列值zk，zk+1，其中zk=H3(zk+1)计算，g=e(P，P)，随机选取，计算：

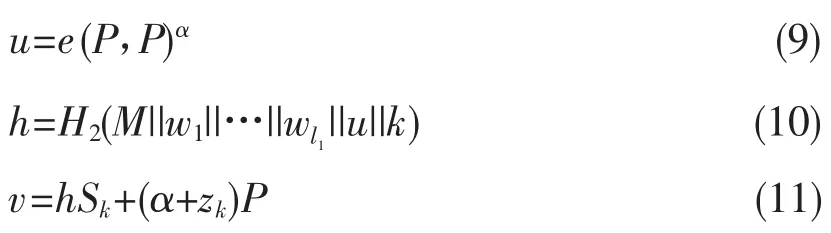
公开(u，v)。

3)B得到全部vj以后，计算等式(12)确定vj的有效性，其余原始签名人计算等式(13)确定v的有效性:

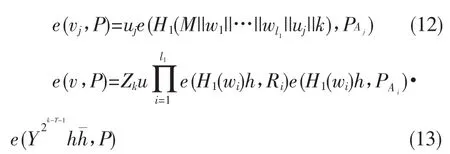
如果所有vj，v都是有效的则B计算：

那么最后生成的签名为：(k，wi，，uj，u，M，Zk，zk+1)(0≤i≤l1，l1＜j≤l1+l2).

2.5 验证签名

签名验证人D得到(k，wi，，uj，u，M，Zk，zk+1)签名后，先比较时间段k与真正的时间段值是否一致，如果不一致则认为签名无效。如果一致，则阅读委托授权信息wi，看委托权限是否超出范围或者代理权是否过期，如果委托权限超出范围或代理权过期则拒绝接受签名，否则，算出h，并计算下列等式：

若等式成立再验证zk+1正确性，若下式成立

则D认为签名有效。

3 可行性证明

定理1若文中(15)式成立，则混合代理签名(k，wi，，uj，u，M，Zk，zk+1)是有效的。

证明：

此式成立说明混合代理签名(k，wi，，uj，u，M，Zk，zk+1)是有效的。

定理2若(16)式，(17)式成立，则混合代理签名(k，wi，，uj，u，M，Zk，zk+1)中zk+1是正确的。

证明：

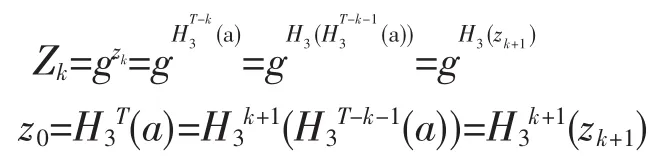
以上两式成立说明zk+1是正确的。

4 安全性及效率分析

前向安全性：若k时间段B的签名密钥泄露，攻击者想要获得k时间段之前的签名秘钥需要解模合数平方根问题，其困难性等价于因子分解问题，因此不可能成功。代理签名是前向安全的。

后向安全性：若第k时间段B的签名密钥泄露，攻击者想要伪造第k+1时间段签名必须要知道zk+2，但是散列函数是单向的，由zk+2容易计算出zk+1，通过zk+1计算出zk+1是不可行的，任意伪造一个z'k+2也无法通过验证等式，保证了方案的后向安全性。

抵抗伪造攻击：攻击者在没有获得k时间段的代理密钥时不可能伪造签名，如果攻击者获得了k时间段的代理密钥，那么由前向安全性和后向安全性的分析可知，签名是前向安全和后向安全的，攻击者不能伪造过去和未来时间段的签名。

其他安全性：委托授权信息wi(0≤i≤l1)在验证等式中出现，验证人能够识别原始签名人和代理签名人的身份以及委托权限和有效期；参加签名所有人的公钥也在验证等式中出现，验证人可以确认签名的正确性；以上分析的两个方面保证了签名的可验证性、不可否认性也能防止代理权的滥用。

效率分析：方案中主要涉及的运算包括双线性对运算、群G1上的乘法运算、群G1上的加运算和Zq上的乘法运算，分别用Pa、Pm、Ad、Mu表示。其中委托代理权的原始签名人数量为m,参加签名的原始签名人数量为n，由于散列运算速度相对其他运算速度较快，所以不计散列运算的计算量。那么本文方案和文献[12]方案的计算复杂度分析如表1。

表1 本文方案和文献[12]计算复杂度

本文的方案在文献[12]方案的基础上增加了单向散列链，虽然少量增加了双线性对和标量乘法运算，计算量有所增加，但是能够使方案具备后向安全性。

5 结语

本文利用单向散列链，设计了一个混合代理多重签名方案。新方案既有原方案的前向安全性又增加了后向安全性，如果当前时间段密钥丢失，今后时间段签名也不会被假冒，最后对安全性和效率做了分析。本文的方案较复杂，下一步的研究方法是考虑如何设计更加简单高效的签名方案。

[1]RiVest R L,Shamir A,Adleman L.A method for obtaining digital signaures and public key cryptosystems[J].Communications of the ACM,February 1978,21(2):120-126.

[2]Mambo M,Usuda K,Okamoto E.Proxy signature: dellegation of the power to sign messages[J].IEI-CE Trans Fundamentals,1996,79(9):1338-1354.

[3]伊丽江,白国强,肖国镇.代理多重签名[J].计算机研究与发展,2001,38(2):204-206.

[4]祁传达,陶建平,金晨辉.一个安全的多重代理签名方案[J].计算机应用研究,2006,23(4):110-111.

[5]李传目.多重代理多重签名方案[J].计算机工程,2003,29(21):43-44.

[6]Zhang J.Improvement of a forward-secure multi-proxy signature scheme[J].Journal of Networks,2011,6(9): 1272-1279.

[7]Huang P H，Wen H A，Wang C H,et al.Proxy multisignature schemes[J].Informatica,2007,18(1):55-60.

[8]Tiwari N，Padhye S，He D.Efficient ID-based multiproxy multisignature without bilinear maps in ROM[J].Annals of telecommunications,2013,68(3-4):231-237.

[9]Wang Z C,Qian H F,Li Z B.Hybrid proxy multisignature:a new type multi-party signature[J]. Information Sciences,2007,117(24):5638-5650.

[10]申平,张建中.新的混合代理多重签名方案[J].计算机应用研究,2009,26(2):711-712.

[11]Anderson R.Two remarks on public key cryptology[C] //The Fourth ACM Computer and Communication Security.New York：ACM Press,1997:151-160.

[12]万世昌,程丽红,张珍.前向安全的混合代理多重签名方案[J].计算机工程与应用,2011,47(12):80-82.

[13]何滨,杜伟章.前向安全无证书代理盲签名方案的分析与改进[J].计算机工程与应用,2013,49(22):104-109.

（责任编辑：李堆淑）

A Backward Secure Hybrid Proxy Multi-Signature Scheme

WAN Shi-chang
（College of Mathematics and Computer Application，Shangluo University，Shangluo 726000,Shaanxi）

A random number is taken as the seed,the hash operation is done continuously,and the orderly hash values generated in the calculation constituted a one-way hash chain.A hybrid proxy multi-signature scheme was designed by the one-way hash chain.The hash value of the current period in the new scheme to participate in the signature calculation and has been verified in the signature verification phase,it ensured the backward security of the scheme.Once the secret keys of proxy signers were lost,signatures of past and future periods can not be forged by an attacker.At last the security and efficiency of the proposed scheme were analyzed.

one-way hash chain;proxy signature;hybrid proxy multi-signature;backward security

TN918.1

A

1674-0033（2015）06-0015-04

10.13440/j.slxy.1674-0033.2015.06.004

2015-10-26

万世昌，男，陕西商南人，硕士，讲师