水文学前沿科学问题之我见

芮孝芳

(河海大学水文水资源学院，江苏南京 210098)

立足于任何一个时代，人们都可以根据对学科的认识程度将其划分为已知和未知2个领域。笔者认为，所谓学科前沿就是指其已知领域与未知领域的“交界面”(图1)。它是从本学科已知领域通向未知领域的前锋，也是一道“屏障”。前沿突破一点，学科的已知领域就将扩充一点，学科因此就会向前迈进一步。因此，所谓学科前沿科学问题必须是那些具有突破价值、能引领学科发展的关键问题。学科前沿是与时俱进的，学科前沿科学问题也必然与时俱进。学科前沿离你有多远与你对学科已知领域了解的广度和深度有关，了解的越广、越深，学科前沿离你也许就比较近，你才有更大的可能找到真正的前沿科学问题，否则就可能遥远一点。一般说来，你在本科学习阶段离学科前沿会远一点，而到了博士论文阶段，离学科前沿就会比较近了。通常所说的热点问题或生产急需问题不一定就是学科前沿科学问题。对于热点问题，一般能列出大量的参考文献。若写成论文发表，也可能有较高的被引率。热点问题的关注度虽高，但却很难断定它一定就是前沿科学问题。对于有些生产急需问题，也许使用现有理论和方法就能很好解决，因此常常不属于前沿科学问题。对于一个前沿科学问题，如果能找到的参考文献很少，甚至连一篇也找不到，那么它有可能就是比较尖端的前沿科学问题。

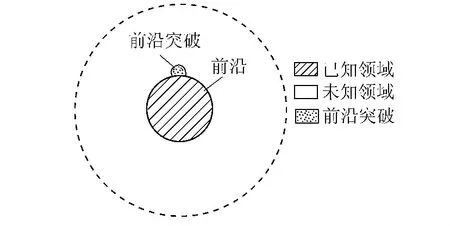
图1 学科前沿示意图

水文学是以水文现象或过程为研究对象的学科。水文现象或过程是大气现象或过程作用于下垫面而发生的。水文学发展到今天，其前沿科学问题是什么呢?笔者以为，水文时间序列年际演变问题、降雨空间分布及动态变化问题、水文现象与下垫面的关系问题、优先流及坡面流问题、水文尺度问题、水文模型的“异参同效”问题、水文非线性问题等可能就是当今水文学面临的主要前沿科学问题。

1 水文时间序列年际演变问题

现代科学认为［1］，地球是一个由岩石圈、水圈、生物圈和大气圈构成的复杂巨系统，其中水圈的结构设想如图2所示。地球系统就水量而言，可认为是一个闭合系统。科学家估算地球系统中气、液、固态水的总储量约为13.86亿km3，这个数据的可靠程度可从表1略知一二［2］。地球系统中的水之所以“取之不尽，用之不竭”，是因为水文循环的存在。地球系统之所以会发生水文循环，一是因为水在常温下就能实现气、液、固三态的相互转变，这是内因;二是因为太阳给地球提供了源源不断的能量，地球自身也有能量产生，又存在地心引力和大气运动，这是外因。内因是水文循环的根据，外因是水文循环的条件。但地球系统就能量而言却是一个开放系统。来自太阳等天体的能量和地球自身产生的能量只有一部分用于支撑水文循环，而且并非固定不变，这样在宇宙中就出现了一个开放的能量系统驱动着一个闭合的水量系统的系统演化问题。

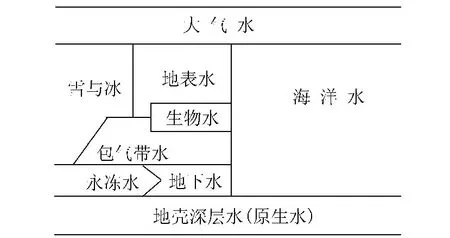
图2 水圈的结构示意图

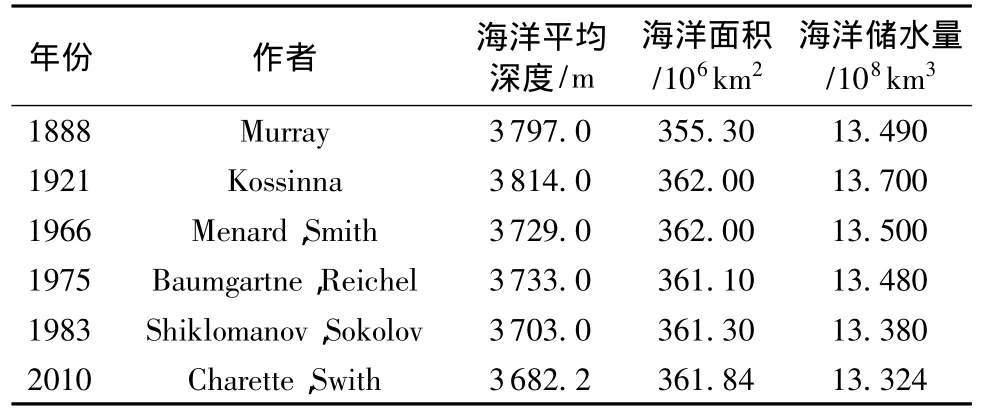
表1 历史上不同作者对海洋储水量的估算

经过漫长的岁月，人们发现水文循环表现为一年一轮回，也就是地球绕太阳公转一周，水文循环就实现一个轮回。如果将从一个雨季到下一个雨季，或者从一个非雨季到下一个非雨季作为一个轮回，那么地球上不同地方轮回的起讫日期是不一样的。地球系统水文循环每经过一个轮回，就会在地球上每个地方产生一个水文要素随时间的变化过程，其年值、月值、每个截口，以及不同历时的年极值均是水文循环每轮回一次的结果。年复一年，这样就形成了水文要素的年时间序列。根据人类对地球形成几十亿年以来的认识和积累的大量历史观测资料所进行的分析，这些水文年时间序列年际演变的基本表现形式是:既不可能单调增加，也不可能单调减小;既不完全相互独立，也不呈函数关系;是起伏性轮回，是不确定性的周期变化［3］。

太阳活动有强弱变化，因此，它提供给地球系统的能量必然在时间上呈不均匀变化。地球由于公转与自转，接收的太阳能又呈动态的空间不均匀分布。这样不仅使每个轮回参与水文循环的水量不同，而且使其时间变化和空间分布十分复杂。对于这样一种十分复杂、开放的地球能量系统驱动着闭合的地球水量系统演变的问题，现代科学还不知道该用什么物理定律和数学方法来揭示和描述它。

自然界发生的一切过程或现象总是有原因的，但不能说都可以通过现有的研究手段将这些原因一一分析出来。对那些能一一分析出原因的过程或现象可以通过实验或理论分析揭示其与过程或现象的定量关系，再建立数学方程式来描述其规律，而对那些还不能一一分析出原因的过程或现象，这样的研究思路就无法使用了［4］。前者是还原论的思维方法，对自然界许多过程和现象，这种方法已获得了极大的成功;对于后者，还原论思维方法则基本上是无效的。笔者认为，水文年时间序列的演变就属于后一种过程和现象，看来人们不能指望用还原论来揭示水文年时间序列的演变规律了。有些科学家认为，对于后一种自然过程或现象，可使用整体论思维方法揭示其规律，但欲在这方面有所建树，任重而道远。这就是当前中长期水文预报精度不高、旱涝发生规律难以掌握、防洪标准有相当大的不确定性、未来水资源量不可作出确定性预测的根本原因。在水利规划设计中认为水文年时间序列为纯随机变化并可用分布函数描写其规律的想法，至今无法得到实验和理论的支撑，只能视作一种尚未严格证明的假设。

笔者曾设想在实验室内通过模拟不同的太阳活动条件和地球公转、自转来进行水文循环实验，生成水文年时间序列的时间变化和空间分布，从而揭示地球上不同地点的旱涝及水文极值发生机理。

2 降雨空间分布及动态变化问题

对于降雨空间分布，下列函数关系是其数学表达:

式中:x，y分别为地球表面一点位置的横坐标和纵坐标;P为该位置点上一定时段的雨量或平均降雨强度，称为点雨量或点雨强。

众所周知，式(1)的解析式至今几乎无法严格给出。因此，在实用上或常规的研究中一般采用下列方法之一来表达降雨空间分布:①等雨量线法，即将空间点上降雨量或降雨强度相同的点连接成互不相交的光滑曲线，通过这些光滑曲线在地球表面的分布来了解掌握降雨的空间分布情况;②降雨斑块图法(图3)，即将空间划分成网格，认为网格内的降雨量或雨强相同，通过这样的斑块图在地球表面的分布来了解掌握降雨的空间分布情况。等雨量线法认为降雨是一种非分区性水文要素，随空间是渐变的。降雨斑块图法则认为降雨量是一种分区性水文要素，随空间可能是突变的。这2种表达降雨量空间分布方法的依据显然相悖。目前仍广泛使用的泰森多边形式实际上是一种最简单的斑块图方法。

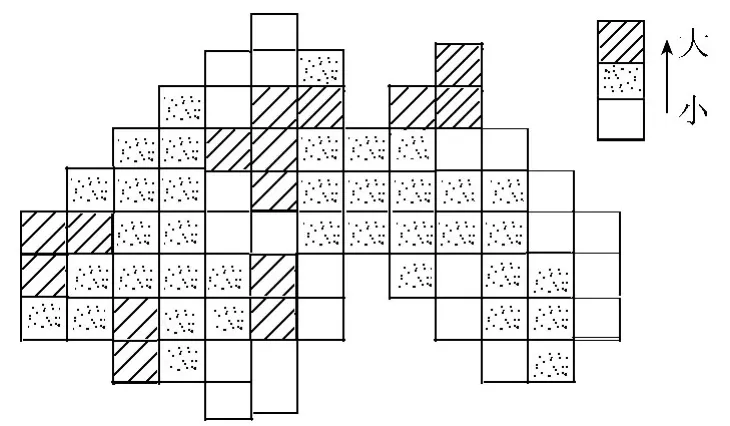
图3 降雨量或强度的斑块分布

现行获得等雨量线或者斑块图的方法主要是通过布设雨量站网，由于雨量站网的密度总是有限度的，所以，在实际工作中要得到等雨量线或斑块图必须进行内插或外推。内插或外推等雨量线一般采用相邻雨量站之间雨量或雨强呈线性变化的假设，而内插或外推斑块图一般采用雨量或雨强与相邻雨量站之间的直线距离平方成反比的假设。无论哪种方法，在使用中都应该考虑地形高程对降雨的影响。

更确切地说，降雨量或雨强不仅表现出空间分布不均匀，而且对不同时刻、不同时段或不同次降雨，这种空间分布不均匀也是变化的。这就是说降雨空间分布不均匀是时变的、动态的。考虑到这一特点，应改用下式来描述降雨空间分布:

式中:t为时间;其余符号的意义同式(1)。

对于式(2)，人们更无法给出其解析式。

很长时间以来，科学家试图通过新的技术来解决动态降雨空间分布的描述问题。雷达测雨技术的兴起就是其中之一。但迄今为止，对于雷达测雨技术，科学家只是揭示了其理论原理，仅导出了雷达气象方程。由于测雨的精度较差，雷达测雨技术目前几乎无法用来测定降雨量，而只能作为一种定性监控雨区范围和暴雨中心移动方向的手段。由于卫星遥感理论和技术的发展，人们又将降雨空间分布及动态变化定量描述的解决寄希望于遥感测雨技术。

降雨空间分布尤其是动态空间分布，至今无法准确掌握和描述，雨量及其过程的测算精度远不及流量和流量过程的测验精度，这就给水文学的许多研究结果增添了不确定性，单位线、等流时线、降雨径流关系、流域水文模型结构和参数等的分析都是如此。在实时预报中，降雨的动态空间分布问题更是造成预报结果不确定性的重要原因。

下垫面条件空间分布不均匀性的描述问题，随着数字高程模型技术的使用，已得到较满意的解决［5-6］，受此启发，人们有理由期待科学家终有一天会找到更好地描述动态降雨空间分布的理论和技术。

3 水文现象与下垫面的关系问题

水文学家认为，自然界水文现象或过程虽然是大气过程作用于下垫面的产物，但两者对水文现象或过程形成的贡献是不同的。如果下垫面条件对水文现象或过程不起作用，那么水文现象或过程必将完全取决于大气过程，但事实不是如此，这就说明下垫面条件是导致水文现象或过程与大气过程不一致的根本原因。相同时空分布的净雨输入相同面积、相同坡度、不同形状水系的流域形成的流域出口断面流量过程线很不相同，就是一个凭借水文常识就可以判断的下垫面条件对水文现象或过程有决定性影响的典型例子(图4)［2］。由图4可见，扇形水系形成的流域出口断面流量过程线峰值最大、峰现时间最早，羽毛状水系形成的流域出口断面流量过程线峰值最低、峰现时间最迟，混合状水系则介于两者之间。

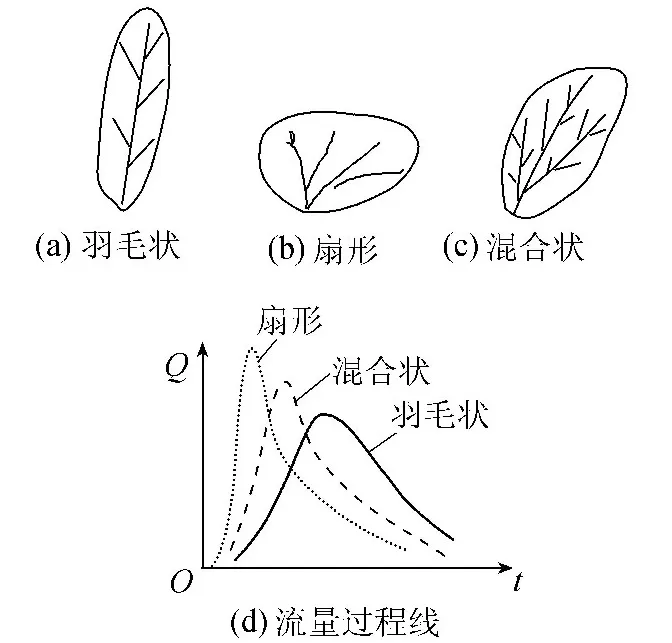
图4 面积和坡度相同时水系形状对流域出口断面流量过程的影响

水文现象或过程与下垫面的关系揭示的是水文要素或参数与下垫面特征值之间的物理联系和定量关系，这个研究领域目前已取得一些成果，示例如下:

a．Muskingam 法参数 x［1］:

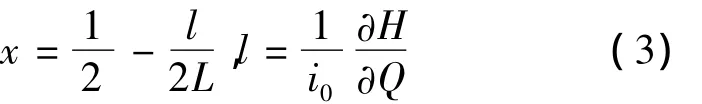
式(3)中的河段长L、河底坡度i0、水位流量关系的水位H对流量Q的一阶导数等是下垫面条件。

b．J 模型参数 j［1］:

式(4)中的流域宽度W、含水层厚度D、给水度μ、渗透系数K等是下垫面条件。

c．流域瞬时单位线峰值um:

对于一些自相似河网，Menabde等［7］于2001年导出um与流域面积A呈下列幂函数关系:

当为MV自相似河网时，可以证明 α=a1－0.63，β=0.63;当为Peano自相似河网时，可以证明α=a0－0.79，β=0.79。这里流域面积A和水系中每条河链的平均集水面积a0均为下垫面条件。

d．Nash模型参数n和k:

Nash于1960年利用英国资料给出了下列关系式:

式(6)中的流域面积A和流域坡度S都是下垫面条件。

e．地貌瞬时单位线的峰值和峰现时间:

Rodriguez-Iturbe等［9］于 1979 年曾给出下列关系式:

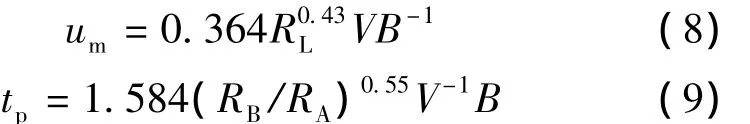
式(8)和式(9)中的 Horton 地貌参数 RB、RA、RL，以及流域长B均为下垫面条件。

获得以上这些流域水文现象或过程与下垫面条件之间定量关系的途径可归纳为物理基础和统计综合分析两类［10］。式(1)～(3)是根据物理定律或物理基础从理论上导出的，而式(4)、式(5)则是由统计综合分析得出的。基于基本的物理定律，补充水文本构关系，而得出水文要素、参数或特征值与下垫面条件的定量关系，称为具有物理基础的途径。通过对水文和下垫面资料的分析，寻找出影响水文要素、参数或特征值的下垫面条件，建立它们之间的经验定量关系，称为统计综合途径。

水文要素、参数或特征值与下垫面条件之间关系的被揭示，尤其是与地形地貌之间关系的被揭示，有力地促进了传统地貌学朝定量地貌学方向发展，使定量地貌学成为水文学家和地貌学家共同的科学问题。正如Bras［11］所言，定量地貌是“水文学最引人入胜的尖端之一”，它支撑了地貌水文学的兴起与发展。地貌水文学兴起于20世纪40年代，以Horton地貌定律的提出为标志，半个多世纪以来，主要的发展是探讨了自然界二分叉水系的形成机理、流域地形地貌对水文过程的作用、反映这种作用的地形地貌特征的定量及提取等。自从Miller于20世纪60年代初创建的数字高程模型(DEM)引入水文学和地貌学后，提取流域地形地貌定量特征的技术有了突破性的发展。基于DEM不仅使传统的寻找分水线、量算流域面积等变得十分快捷方便，而且使以往难以实现的提取流域坡度分布、地形指数分布、Horton地貌参数、流域基本单元、宽度函数、水滴向流域出口断面汇集路径等得以迎刃而解。DEM还为考虑土壤、植被等空间分布对水文现象或过程的作用提供了技术支撑。那种仅依靠气象和水文观测资料分析水文过程、水文学被人称为经验“系数科学”的时代将成为历史。

回想起人们在探索水文规律、解决实际问题过程中所表现出的不得不极强地依赖水文资料的无奈，以及在缺乏资料和人类活动影响强烈地区解决水文问题所感到的“巧妇难为无米之炊”的尴尬，人们就会更加觉得揭示和建立水文与下垫面条件的定量关系，根据下垫面条件和大气过程就能推求水文过程，减少解决水文问题对水文资料的依赖是多么的重要。这是水文学家长期坚持追求的目标，也许也就是PUB(无资料流域水文预报)计划的初衷。

4 优先流及坡面流问题

土壤是结构复杂的多孔介质，其复杂性不仅在于是基质结构，而且在于存在多原因形成的水流优势的通道。水在重力、毛管力和分子力作用下向土壤中下渗，当遇到这些优势通道时，就会绕过土壤基质，以比在土壤基质中快得多的速度通过这种导水能力极强的优势通道，向土壤深部或地下水下渗的水流称为优先流［12-13］。优先流的形成十分复杂，现代科学还不能完全说清楚其形成原因和发生、发展条件，据说土壤孔隙度和渗透性的不均匀分布、非饱和土壤中孔隙水的不均匀分布、土壤水的滞后效应、非饱和土壤中的气流等都可能导致优先流。在实验室实验中甚至还发现在宏观均质土壤中也会发生优先流。优先流的存在大大加快了水向土壤下渗的速度和在土壤中渗透、渗漏的速度，对建立在Darcy定律和Richards方程基础上的下渗理论，及建立在Horton产流理论和Dunne产流理论基础上的径流形成理论都是严重挑战［14］。

早在20世纪40～50年代，学术界就有坡面流是“片流”还是“沟流”的讨论。“片流”论者认为坡面流是二维平面上的连续介质水流。“沟流”论者认为坡面流是由一维连续介质水流构成的“网状”水流。笔者认为，无论是“片流”论，还是“沟流”论，似乎都没有抓住坡面流的主要特点。事实上，由于受到微地形和各向异性覆盖物的影响，坡面好似不规则编制成的“地毯”。水滴穿行其间，其流动特点似乎应该介于明渠水流和多孔介质水流之间。由Chezy公式可知，明渠水流流速与水深和水面比降乘积的1/2次方成正比。由Darcy公式可知，饱和土壤水流只与地下水面坡度的一次方成正比。若将明渠水流流速公式和饱和土壤水流流速公式写成统一形式，则有

式中:V为水流流速;i为水面坡度;对于饱和土壤水流，β=1，α为饱和水力传导度，与水深无关;对于明渠水流，β=1/2，α为水深和糙率的函数。

众所周知，自然界存在的真实坡面流一般是观测不到水深的，因此，一般的猜想是坡面流的β应在1/2～1之间，α可能仅与糙率有关，“水面坡度”则由“地形坡度”取代［15-16］。笔者期待用实验来验证这个猜想，而实验的困难在于如何测定坡面流速。

揭示坡面流速规律的重要性，从下面例子可见一斑［17］。2008年，笔者曾建议一种基于网格“水滴”的流域汇流计算方法。将流域划分成许多网格，取一个合适的网格尺寸就可将其拥有的净雨量视作一个“水滴”。然后寻找出每个网格“水滴”汇集至流域出口断面的路径。如果再确定出“水滴”通过每个网格的速度，那么就可以得出每个“水滴”到达流域出口断面的汇流时间。将那些不同时刻落地的净雨“水滴”，按同时刻到达流域出口断面进行相加，就可得出一场净雨形成的流域出口断面流量过程。这种方法不仅吸取了等流时线法和单位线法各自的优点，克服了各自的缺点，而且将Lagrange着眼于“粒子”的流体力学分析法和Euler着眼于“场”的流体力学分析法统一起来。这里需要解决的关键问题就是确定网格“水滴”的流速。坡面流速问题因此而显得十分重要。

5 水文尺度问题

“尺度”在词义上虽有“大小”之意，但作为一个科学术语，不可简单理解为“大小”，而是表达了人们观测自然现象的时空观，即指人们在研究自然现象时所采用的空间范围和时间长短。不同时空尺度对现象的观测，可能有不同特点，也可能存在一定的联系。

尺度问题包括尺度效应和尺度转换［18-19］。若现象或过程的特点随观测的尺度而变化，则称这样的现象或过程具有“尺度依赖性”(scale dependent)或“尺度效应”。反之，称为“尺度不变性”。尺度效应的发现可追溯到Mandelbrot［20］提出的“英国的海岸线有多长”的问题。尺度效应的研究目的是发现那些具有尺度依赖性的现象或过程。对不同尺度下观测的现象或过程之间的关系进行识别、推断、推绎称为“尺度转换”(scaling)，也称为“标度化”或“尺度推绎”。尺度转换问题可分为升尺度转换即尺度上推(scaling-up)和降尺度转换即尺度下推(scaling-down)两类基本问题。前者是指将小尺度(高空间分辨率、小空间范围)上观测的现象或过程推绎到大尺度(低空间分辨率、大空间范围)。后者则相反，是指将大尺度上观测的现象或过程分解到小尺度。

水文学通常会遇到两类尺度问题:现象或过程的尺度问题和地形地貌特征值提取的尺度问题。前者可以揭示流域降雨径流形成规律为例来说明。人们认识流域降雨径流形成规律一般从分析一定尺度流域的实测资料入手。由于地球上不同尺度的流域总数可认为是无穷无尽的，人们根本无法通过设置水文气象站网、积累观测资料来认识、揭示每个流域的降雨径流形成规律，而只能对其中为数不多的流域进行这样的分析研究。建立或验证流域水文模型也有类似情况。因此，寻求流域降雨形成规律或流域水文模型参数的尺度依赖性和尺度转换方法至关重要。如果某种自然现象服从相似规律，那么该自然现象在不同尺度表现出来的差异就可以通过几何相似比例来决定［21］。但对于水文现象或过程，即使流域几何相似，也几乎不可能导出其相似条件，究其原因，一是因为空间异质性问题，一般言之，随着尺度增大，由于很多细节会忽略，空间异质性会降低，非线性特征也会下降，线性特征会增强。二是调蓄或均化问题，一般言之，随着尺度的增大，变化率高的将会被抹除，而变化率较低的将会得到保留，其作用得到凸现。后者是指人们在提取流域地形地貌特征值时总是要依据一定比例尺的地形图或一定分辨率的DEM，以及需要选用量取的分划长度。以提取长度为例，如果采用的地形图已定，那么由不同分划长度量取所得的河长是不同的。理论上只有当分划长度趋于零时所得极限才是“真实”的河长，但由分形理论可知，这样的极限是不存在的［20］，以致河长的“真值”永远是未知的。如果采用的分划长度已定，那么由不同比例尺地形图获得的河长也是不同的。因此，笔者认为，在这种情况下，人们在提取地形地貌特征值时就要规定一个“标准”，即规定一定比例的地形图或一定分辨率的DEM，以及一定长度的分划值，而对于那些不符合这个标准提取的地形地貌特征值应进行尺度转换。

6 水文模型的“异参同效”问题

如果模型只有一个参数，那么只要目标函数存在极值，极值就一定是唯一的。但如果模型包含2个或2个以上参数，情况就复杂了。以2个参数为例，其响应面就可能呈现3种情况(图5):①响应面近似同心圆(图5(a))。这表明最优参数组只有一组，它就是使目标函数取得极值的唯一参数组;②响应面存在一条脊线或凹槽线(图5(b))，这表明目标函数的极值不收敛于一个点，而收敛于一条线，将有无穷多组参数使目标函数达到相同的极值，也就是使目标函数取得同一极值的参数组不是唯一的;③响应面存在多于一个同心圆(图5(c))。这表明有多于一组参数使目标函数达到相同或不相同的极值，此时，若极值为有限个，因能找到最小的极值，故也属于有唯一一组参数值使目标函数值最小的情况。出现以上第二种情况和第三种情况中极值数目不确定者称为“异参同效”现象。

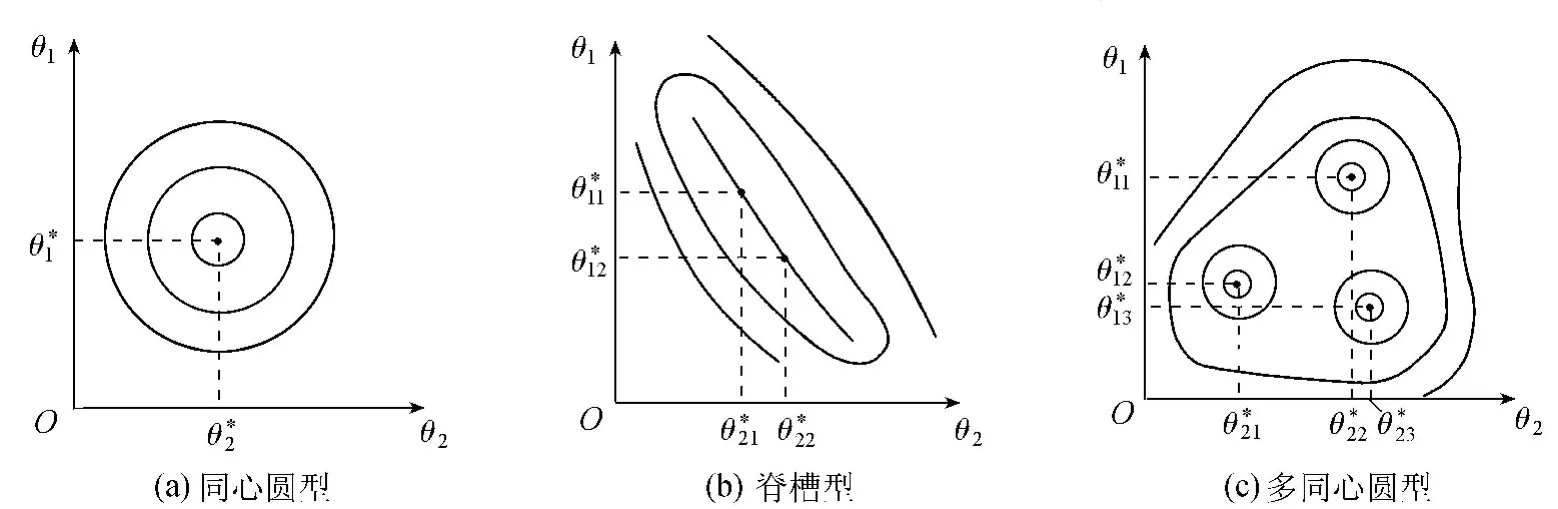
图5 两参数模型的响应面

响应面是最优化方法的直观表达方式，但只有当模型仅包含2个参数时适用。大多数流域水文模型都有2个以上参数需要通过率定确定。为此，水文学家提出了多种揭示多参数模型“异参同效”现象的方法，GLUE法就是其中之一。它是 Beven等［22］于1992年提出的方法。据说Beven等提出的该方法原本是用来分析参数灵敏性的。但笔者认为，该方法也是一个识别“异参同效”的方法。该法基于Monte-Carlo统计试验法的思路，在模型参数可能取值范围内，随机抽取数量庞大的参数组，然后对其中每一个参数组，计算模型的似然函数(目标函数值)，并点绘参数组中每一个参数与似然函数值的散点图。这种散点图表明对应于某个参数的一定值将会与其他参数构成大量的参数组，计算相应的似然函数值，其中必有一个极值与之相对应。这种散点图一般会呈现出3种情况(图6):①似然函数值随某个参数值变化存在一个明显极值(图6(a))，这样的参数显然属于较灵敏的参数。②似然函数值随某个参数值几乎不变化(图6(b))，这样的参数显然属于不灵敏参数。③似然函数值随某个参数值变化呈多次起伏变化(图6(c))，这样的参数显然使似然函数出现多于一个极值。如果通过GLUE方法分析，发现模型中每个参数的散点图都属于以上第一种情况，那么说明对该模型来说能找到唯一的一个参数组使似然函数值达到极值。如果通过GLUE方法分析，发现模型中有部分参数或全部参数的散点图属于以上第二种情况，那么对模型来说，能使似然函数值达到极值的参数不是唯一的。如果通过GLUE方法分析，发现模型中有参数会使似然函数值出现多个极值，那么也表明最优参数组不是唯一的。

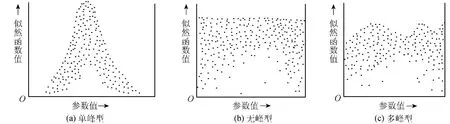
图6 参数值与似然函数值的散点图

水文模型的“异参同效”就是模型解的不唯一性，也就是解的不确定性。由于这个缘故，“异参同效”分析又称为模型不确定性分析。但应指出［23］，模型解的不确定性与自然现象的不确定性不同源，不可混为一谈。

朱君君［24］曾通过实测资料和理想资料的对比分析，初步揭示了“异参同效”产生的原因。理想资料相对于实测资料，是不受资料误差、模型结构不合理影响的，因此，理想资料的“异参同效”显然来源于参数之间的互补性、不敏感参数和似然函数的多极值性。实测资料的“异参同效”程度明显大于理想资料的“异参同效”程度，表明造成“异参同效”问题除以上原因外，还包括模型结构的不合理和实测资料的误差。

为了克服水文模型的“异参同效”问题，水文学家针对其产生的原因做了一些尝试。克服模型结构的不合理性、不将不敏感参数作为待率定参数、避免使用多极值目标函数、分阶段或子过程设置目标函数以尽量减少目标函数包含的参数、尽可能采用物理方法确定模型参数、设法弱化模型参数之间的互补性、减少模型输入和输出资料的误差等都是理论上克服“异参同效”问题的措施。

当前面临的事实是:现在离解决“异参同效”问题还有遥远的路程。“异参同效”问题是水文模型应用的一个“结”，只有设法解开这个“结”，水文模型才能展示出重要的作用和强大的生命力。

7 水文非线性问题

广义的“线性”和“非线性”属于哲学术语。认为系统初始状态变化所导致的后续变化是成正比例的思维称为线性系统思维，它是一种逻辑思维。认为事物是一个整体性的复杂系统，其中部分功能之和不等于整体功能，诸多相互关联的因素不满足叠加原理的思维称为非线性系统思维，它是一种非逻辑思维。数学和物理学中的“线性”和“非线性”是狭义的“线性”和“非线性”，一个现象或过程是线性的，它必须满足叠加性和均匀性或倍比性。一个现象或过程虽满足叠加性但不满足均匀性，或者既不满足叠加性也不满足均匀性，则称为非线性。

如前述，水文现象或过程是大气现象或过程作用于下垫面条件的产物，写成函数形式为

式中:R为水文现象或过程;M为气象现象或过程;θ是下垫面条件。

从因果论理解式(11)，气象现象或过程是“作用”，下垫面是“被作用体”，水文现象或过程则是“作用”施加于“被作用体”产生的结果。从系统论理解式(11)，气象现象或过程就是“输入”，下垫面就是“系统作用函数”，水文现象或过程则是系统的“输出”。从模型论理解式(11)，气象现象或过程就是“激励”，下垫面条件就是“参数”，水文现象或过程则是“响应”。

不难理解，式(11)实际上是描述气象现象或过程、下垫面条件和水文现象或过程三者之间物理联系的微分方程的一个解。笔者发现，数学家所谓解微分方程与物理学家、工程师所谓解微分方程是不完全相同的。数学家认为只有建立了微分方程才能求得其解，而物理学家和工程师认为除了可通过建立微分方程求得其解外，还可以在无法建立微分方程的条件下通过对现象或过程及其相关影响因素的观测和分析给出其近似解。

在式(11)中，如果包含有关于未知变量及其各阶导数的二次方以上的项，或者其系数是未知变量的函数，那么就是非线性的，它所描述的问题就是非线性问题;如果只包含未知变量及其各阶导数的一次方项，而且其系数与未知变量无关，那么就是线性的，所描述的就是线性问题。

水文非线性问题起源于 2 个方面［1，25-27］:一是物理定律及本构关系，二是下垫面条件是否随水文现象或过程而变。它们共同决定了微分方程中未知变量及其各阶导数的方次及微分方程中各系数是否与未知变量有关。

现代数学和物理已经比较圆满地解决了线性问题，但对非线性问题除了个别特例外仍是一筹莫展，这也是为什么总是将非线性问题近似成线性问题来解决的主要原因。由于将非线性问题近似成线性问题必然会带来误差，甚至会带来不合理的结果，因此，在对水文学应用提出更高精度要求的今天，寻求更好的非线性问题解法已难以回避。

8 结语

笔者有幸置身于一个科学技术突飞猛进、空前繁荣的时代，积半个世纪学习、研究、实践水文学理论和方法之心得体会，尝试提出了若干水文学前沿科学问题，论述了各自的科学内涵、突破的可能切入点，以及对水文学发展的推动作用。笔者所论难免挂一漏万，仅为抛砖引玉而已。笔者的信念是:只要这些前沿科学问题有所突破，水文学就可能向前发展一大步。笔者深切期待有更多的水文学者，尤其是青年学者来关心、发现、探讨水文学前沿科学问题。

［1］芮孝芳．水文学原理［M］．北京:高等教育出版社，2013．

［2］CHARETTE M A，SMITH W H F．The volume of earth’s ocean［J］．Oceanography，2010，23(2):112-114．

［3］陈泮勤，程邦波，王芳，等．全球气候变化的几个关键问题辨析［J］．地球科学进展，2010，25(1):69-75．(CHEN Panqin， CHENG Bangbo， WANG Fang， et al．Discrimination on several Key issues of global climate change［J］．Advances in Earth Science，2010，25(1):69-75．(in Chinese))

［4］常绍舜．从整体与部分的辩证关系看系统论与还原论的适用范围［J］．系统科学学报，2008，16(1):87-89．(CHANG Shaoshun．Applying Area of the System Theory and Reductionism from the Point of View of the Interplay between the Whole and the Part［J］．Chinese Journal of Systems Science，2008，16(1):87-89．(in Chinese))

［5］芮孝芳，石朋．数字水文学的萌芽及前景［J］．水利水电科技进展，2004，24(6):55-58．(RUI Xiaofang，SHI Peng．Seeds and prospects of digital hydrology ［J］．Advances in Science and Technology of Water Resources，2004，24(6):55-58．(in Chinese))

［6］宫兴龙．流域地貌特征及流域地貌单位线研究［D］．南京:河海大学，2009．

［7］MENABDE M，VEITZER S，GUPTA V，et al．Tests of peak flow scaling in simulated self-similar river networks［J］．Advances in Water Resources，2001，24(1):991-999．

［8］NASH J E．A unit hydrograph study，with particular reference to british catchments［J］．Proceedings of the Institution of Civil Engineers，1960，17(3):249-282．

［9］RODRIGUEZ-ITURBE I， VALDES J B． The geomorphologic structure of hydrologic response［J］．Water Resources Research，1979，15(6):1409-1420．

［10］芮孝芳，蒋成煜．流域水文与地貌特征关系研究的回顾与展望［J］．水科学进展，2010，21(4):444-449．(RUI Xiaofang，JIANG Chengyu．Review of research of hydrogeomorphological processes interaction［J］．Advances in Water Science，2010，21(4):444-449．(in Chinese))

［11］BRAS R L．Hydrology ［M］．Reading，MA:Addison-Wesley，1990．

［12］ALLAIRE S E，ROULIER S，CESSNA A J．Quantifying preferential flow in soils:a review of different techniques［J］．Journal of Hydrology，2009，378(1):179-204．

［13］牛健植，余新晓．优先流问题研究及其科学意义［J］．中国水土保持科学，2005，3(3):110-116．(NIU Jianzhi，YU Xinxiao．Preferential flow and its scientific significance［J］．Science of Soil and Water Coservation，2005，3(3):110-116．(in Chinese))

［14］张小娜．大孔隙土壤的产汇流模型和溶质流失模型研究及实验验证［D］．南京:河海大学，2010．

［15］张金存．基于下渗理论的网格型松散结构分布式水文模型研究［D］．南京:河海大学，2007．

［16］刘宁宁．Lattice Boltzmann方法改进及其在城市雨洪模型中的应用研究［D］．南京:河海大学，2012．

［17］RUI Xiaofang，YU Mei，LIU Fanggui．Calculation of watershed flow concentration based on the grid drop concept［J］．Water Science and Engineering，2008，1(1):1-9．

［18］SPOSITO G．Scale dependence and scale invariance in hydrology［M］．New York:Cambridge University Press，1998．

［19］GUPTA V K，RODRIGUEZ－ITURBE I，WOOD E F．Scale problems in hydrology［M］．Boston:D．Reidel Publishing Company，1986．

［20］MANDELBROT B B．How long is the coast of Britain［J］．Science，1967，155:636-638．

［21］列兹尼亚科夫 A G．相似方法［M］．王成斌，译．北京:科学出版社，1964．

［22］BEVEN K J，BINLEY A M．The future of distributed models:model calibration and uncertainty prediction［J］．Hydrologic Process，1992，6:279-298．

［23］张超．流域水文模型参数自动优化率定及不确定性研究［D］．南京:河海大学，2010．

［24］朱君君．Nash模型异参同效问题及参数确定方法研究［D］．南京:河海大学，2011

［25］张东辉，张金存，刘芳贵．关于水文学中非线性效应的探讨［J］．水科学进展，2007，18(5):776-784．(ZHANG Donghui，ZHANG Jincun，LIU Fanggui．Some comments on nonlinear effect in catchment hydrology［J］．Advances in Water Science，2007，18(5):776-784．(in Chinese))

［26］仪垂祥．非线性科学及其在地学中的应用［M］．北京:气象出版社，1995．

［27］ RUI Xiaofang，LIU Ningning，LI Qiaoling，et al．Present and future ofhydrology［J］．WaterScience and Engineering，2013，6(3):241-249．