大直径软岩嵌岩桩嵌岩深度计算模型

赵明华，冯明伟，刘 猛，尹平保，杨超炜

(湖南大学岩土工程研究所，湖南长沙 410082)

随着海洋资源的不断开发利用，临海(河)码头、深海钻井平台、跨海大桥等工程大量开始建设。水上构筑物需承受水流、风、船舶等产生的水平荷载作用，大直径水上嵌岩桩能够很好地满足实际工程需要，从而被广泛利用［1-2］。嵌岩深度作为嵌岩桩设计计算的关键参数，其确定方法仍是学术界研究的热点，国内外学者围绕嵌岩桩做了大量的理论以及试验研究并取得了较多的成果。

经验法认为嵌岩桩嵌入岩层达2～3倍桩径时，即可视嵌岩段达到完全嵌固状态，很显然该方法过于粗糙，只可用于可行性设计阶段。弹性地基反力法分别采用桩土相互作用的刚度(m法)和柔度系数(张有龄法)来确定嵌岩深度，其较经验法相对优越，但仍具有相当的局限性［3］。JTJ 285—2000《港口工程嵌岩桩设计与施工规程》［4］和 JTGD 63—2007《公路桥涵地基与基础设计规范》［5］认为最小嵌岩深度与岩石单轴饱和抗压强度、基岩顶面处基桩受到的剪力和弯矩有关，并给出了详细的计算方法;汪荣麟［6］综合利用m法和C法计算出基岩顶面处的桩身弯矩，适当改进了嵌岩深度设计计算方法;赵明华等［7］考虑了桩身转动以及桩端断面与基岩接触面产生的反力矩等有利条件，得到最小嵌岩深度计算新方法。上述研究均假定嵌岩桩受基岩顶面处剪力和弯矩作用沿嵌岩段桩身中心点转动，但实际工程中桩体不会始终围绕中心点转动，而是随着基岩顶面处剪力和弯矩的变化而不断改变。此外上述研究还假定嵌岩段桩体以桩侧岩石抗压破坏为判据，但牛双建等［8］通过室内试验发现单轴压缩和三轴压缩条件下岩石多发生劈裂和剪切组合破坏模式;Zhang等［9］认为嵌岩段桩侧受到桩前岩体法向正应力和桩侧岩体切向剪应力共同作用且该假定能较好地符合实际工程情况。

为了更好地了解嵌岩桩的工程性质，大量学者通过室内模型试验以及室外现场试验做了相关分析。王多垠等［10］通过室内大比例相似模型试验较好地模拟了港口大直径嵌岩灌注桩横向承载性能，为嵌固在软岩中的嵌岩桩设计计算提供了一定的参考和借鉴;周世良等［11-12］通过室内模型试验及现场数据对比发现多次饱水条件下的桩侧岩石承载能力会急剧下降，并建议软岩地区嵌岩桩的嵌岩深度应有70%的富余;曹雪山［13］通过室内试验指出嵌岩桩的嵌固特性与桩径以及基岩顶面处的剪力、弯矩有关，且嵌岩段以桩体受剪破坏为主;王建华等［14］通过现场试验研究了水平荷载下大直径嵌岩桩的工作机理，试验表明嵌岩段桩侧岩石多处于弹性破坏阶段且桩侧岩石抗力呈线性分布。

本文在已有研究成果的基础上分析嵌岩段基岩顶面处桩体受剪力、弯矩共同作用时嵌岩段的受力特性。考虑嵌岩段桩侧岩石受到桩前岩体法向正应力和桩侧岩体切向剪应力共同作用，结合莫尔二次抛物线判据计算出最大抗力值。根据嵌岩段受力特性并假定嵌岩段桩侧岩石抗力大小呈线性分布得到嵌岩深度计算模型，继而给出嵌岩桩最小嵌岩深度计算方法，同时对影响嵌岩深度的参数进行分析。

1 考虑软岩极限状态的计算模型

1．1 计算模型条件

在已有研究成果基础上，为充分反映极限状态下的大直径软岩嵌岩段桩身与岩体受力特征，同时为避免复杂的运算，现对文本计算模型作如下基本假定:

a．嵌岩桩由于水平力作用而产生水平转动，嵌岩段桩侧岩石受到桩前法向正应力和桩侧切向剪应力共同作用，且桩侧岩石抗力随嵌岩段深度呈线性变化［14］，嵌岩段受力分析如图1所示。图1中PH、MH分别为基岩顶面处的水平力、弯矩;σ1、σ3分别为最大、最小主压应力;σ为桩前法向正应力;τ为桩侧切向剪应力;d为桩径;hr为嵌岩深度;p为嵌岩段桩侧岩石水平抗力;a、b为待定系数，b/a为桩侧水平向应力零点;z为变量，其取值范围为0≤z≤hr。

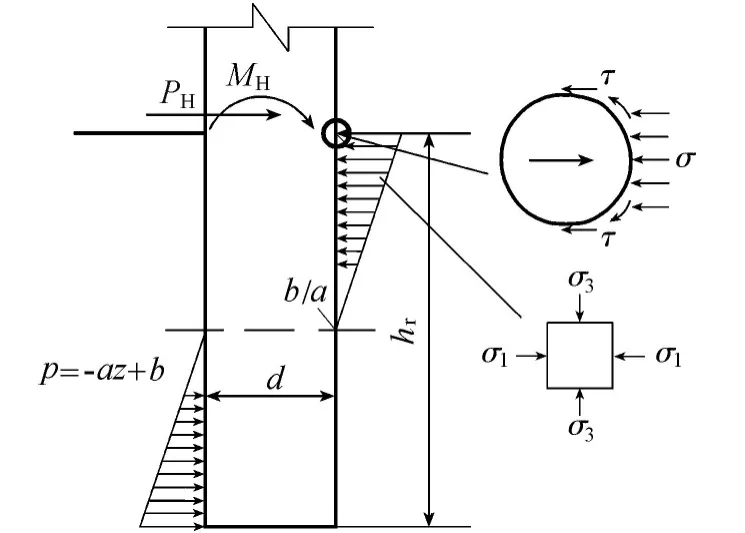
图1 嵌岩段受力分析

b．桩前法向正应力和桩侧切向剪应力的分布均与桩体位移成正比，且按三角函数关系分布［9］，基岩顶面处桩侧受力分析如图2所示。图2中σm、τm分别为基岩顶面处桩侧最大法向正应力、最大切向剪应力;α为桩侧上各点到桩身中心点连线与水平方向的夹角。

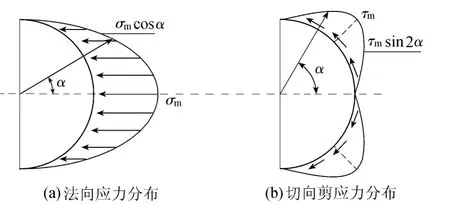
图2 基岩顶面处桩侧受力分析

c．忽略桩端反力的影响［5］。

1．2 桩侧岩石抗力

根据计算模型条件a，嵌岩段桩侧岩石抗力自上而下随深度线性变化，满足:

由于圆形基桩桩身形式的特殊性，桩身每一点的法向应力和切向剪应力必将随α变化，具体变化关系如下:

每个人周围都有一个不可见的空间“气泡”，而且随环境条件的不同发生大小变化，当受到干扰时，人就会感到很不舒服。人在社会环境中存在着密切距离 、个体距离、社会距离和公众距离，在进行社会交往时，人们总是随时调整自己与他人所保持的距离。通过空间的大小、距离，达到使人舒适、平衡的感觉。通过对各个空间的面积以及距离的调查，可看出客厅普片面积较大于其他室内空间，给人营造一种开阔的感觉，而卧室相对客厅较小，让人感觉更加私密，这便是空间的距离感的作用。使人在不同的空间，不同的行为性质下，能够找到合适的空间大小距离进行。

根据图2中的几何关系，可得基岩顶面处桩侧岩石极限抗力pm计算公式为

嵌岩段桩侧岩石剪切破坏满足莫尔二次抛物线型包络线，有

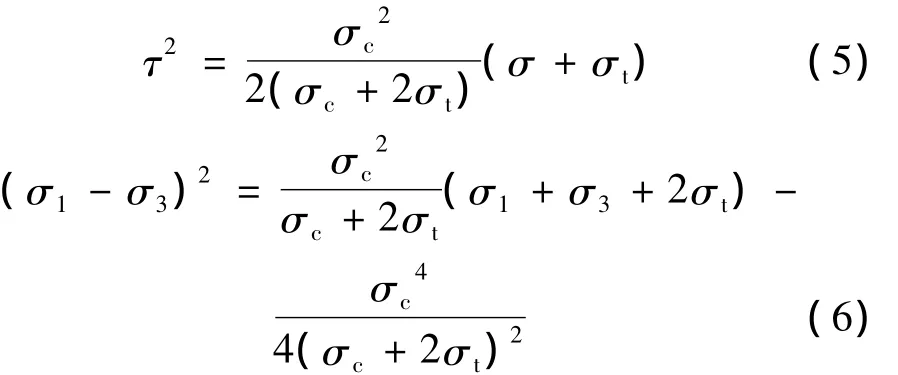
式中σc、σt分别为嵌岩段桩侧岩石饱和单轴抗压、抗拉强度标准值。

当α=0时，最大主应力σ1可视为等于桩侧最大法向正应力σm，最小主应力σ3则为上覆土层的压应力，即

式中:i为土层层数;li为第i层土层厚度;ρi为第i层土层饱和密度。当α=π/4时，桩侧剪应力最大，此时桩侧法向应力大小为

将式(7)(8)代入式(6)，有

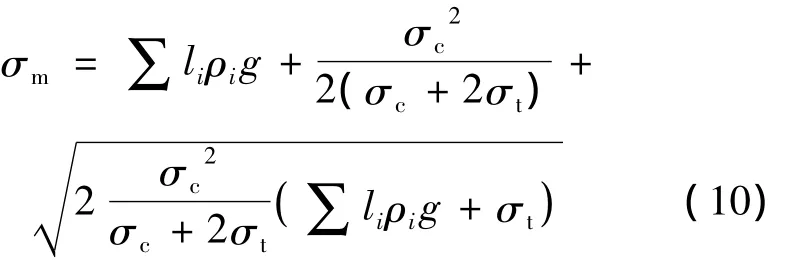
先将式(10)代入式(9)，再将式(9)代入式(5)，有

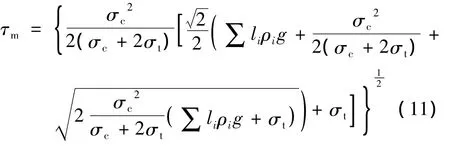
将式(10)(11)代入式(4)，得极限抗力为

当上覆土层厚度较小时，可忽略σ3的影响，式(12)可简化为

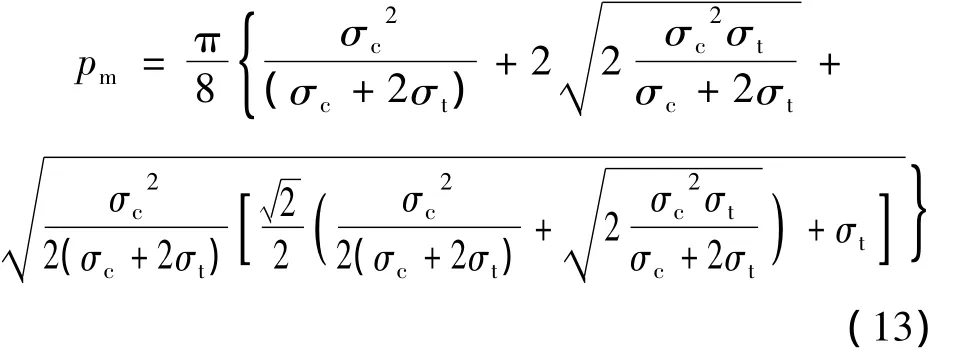
为了保证桩侧岩石能够提供足够的抗力必须满足以下关系:

1．3 最小嵌岩深度

根据前述嵌岩段桩体的受力特性，按桩身稳定方法计算最小嵌岩深度，图1中桩体受力分析如下:水平力平衡条件为

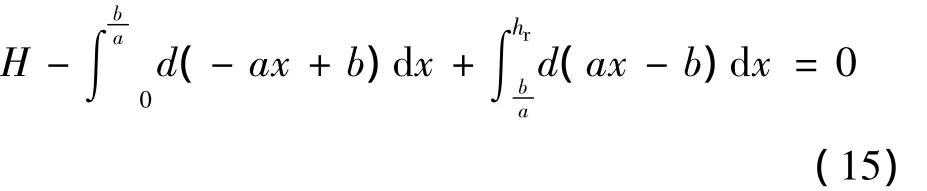
对基岩顶面处桩身中心点取弯矩，有

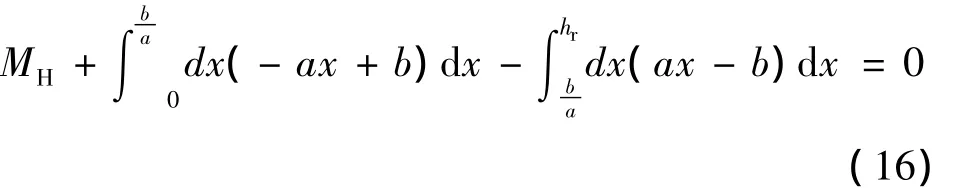
当基岩顶面处岩石受剪切破坏时，联立式(13)～(16)，得最小嵌岩深度为

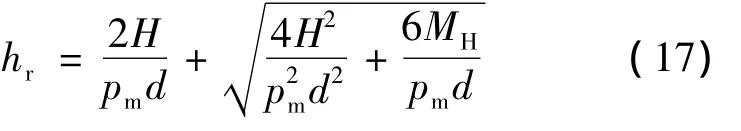
桩侧岩石抗力为

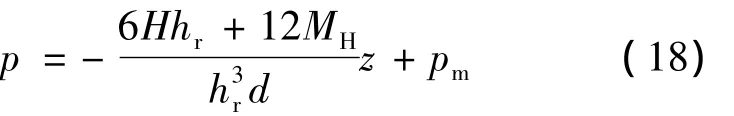
由式(18)可知，桩侧岩石抗力的分布形式与基岩顶面处的水平力、弯矩、嵌岩深度、桩径以及桩侧岩石极限抗力有关。

2 算例分析

为了验证本文模型的可行性，将文献［10］中室内大比例模型试验结果、文献［11-12］的现场工程设计结果与本文模型计算结果进行对比验证，同时将本文模型计算结果与经验法、规范法的计算结果进行对比分析。

2．1 室内模型试验结果

为了研究大直径嵌岩桩在水平荷载作用下嵌岩段桩体与岩石的工作特性，王多垠等［10］根据实际工程进行了室内大比例模型试验，很好地模拟了嵌岩段桩体与桩侧岩石的相互作用关系，主要计算参数如下:桩径为0.09m，基岩顶面水平力为420N，基岩顶面处弯矩为420 N·m，岩石饱和单轴抗压强度为220 kPa、抗拉强度为22 kPa。根据式(17)(18)计算可得嵌岩深度hr=43.8 cm，桩侧岩石抗力计算公式为p=－812.4z+188.5。此时计算所得的嵌岩深度相对实测试验数据较低，原因是文献［10］中室内试验水平推力为420 N时还未完全发挥桩侧岩石的极限抗力，极限水平荷载应稍大于420 N。

2．2 现场工程设计结果

文献［11-12］中云南富宁港建设工程一期工程的设计资料如下:码头嵌岩桩径为1.2 m，基岩顶面处桩身受到剪切应力设计值为1 MN，基岩顶面处桩身弯矩设计值为10MN·m，岩石饱和单轴抗压强度为4210 kPa，上覆土层压应力为400 kPa。由于现场资料缺少岩石饱和单轴抗拉强度，此处综合考虑刘佑荣等［15］关于软岩抗拉强度与抗压强度比值的合理取值范围以及孙丽［16］大量室内试验结果，取σt/σc=0.1，即岩石饱和单轴抗拉强度为421 kPa。根据式(17)、(18)计算可得嵌岩深度hr=3.9 m，桩侧岩石抗力计算公式为p=－2.01z+4.1。

2．3 模型计算结果

将本文模型计算的最小嵌岩深度同常用算法的结果做一详细对比，见表1。

表1 常见嵌岩深度计算方法比较

由表1可以看出，经验法显然过于粗糙，不可作为精确设计方法，对于软岩应保证较大的嵌岩深度。JTJ285—2000《港口工程嵌岩桩设计与施工规程》和JTGD63—2007《公路桥涵地基与基础设计规范》因考虑到基岩顶面处水平力、弯矩以及桩侧岩石单轴饱和强度变化的影响，较经验法相对合理但却过于保守，安全系数较大显得很不经济;由于前者比后者多考虑了基岩顶面处水平力作用，因此其计算的嵌岩深度较后者偏大。本文模型计算的嵌岩深度较规范法减小约50%且与实测嵌岩深度更为接近，从而验证了本文模型的正确性与优越性，可为实际工程节约成本，具有一定的实用价值。

3 参数分析

为分析嵌岩深度与各影响参数的关系，现用上述工程设计数据对嵌岩深度与嵌岩段桩侧岩石的单轴饱和抗压强度σc、基岩顶面处桩身受到的水平力PH、桩径d、上覆土层压应力σ3的关系做相应的参数分析。当桩径d=1.2m，σt/σc=0.1，σ3=400kPa，基岩顶面处桩身受到不同的水平力PH时，嵌岩深度hr与嵌岩段桩侧岩石的饱和单轴抗压强度σc的关系如图3所示。由图3可知，在PH不变的情况下，在一定范围内hr随着σc的增大逐渐减小，但当σc增大到某一定值时，hr呈小幅递减趋势。当PH=500kN、1000 kN、 1500 kN、 2000 kN 时，σc分别大于3750kPa、4500kPa、5250 kPa、7500 kPa 之后，嵌岩深度减小幅度均不超过10%，这主要是因为当桩侧岩石强度较大时水平力不足以使桩侧岩石发生极限破坏。

图3 hr-σc关系曲线

当 σc=4210 kPa，σt/σc=0.1，σ3=400 kPa，桩径d不同时，hr-PH关系曲线如图4所示。由图4可知，hr随着PH的增大而不断增大，随着d的增大而不断减小。当PH一定时，d的增大会使桩岩接触面积增大从而使桩侧岩石抗力随之增大，继而会使hr有所减小。水平荷载PH较大时，在其他条件一定的情况下会导致嵌岩深度hr增大，但hr的增大势必会增加施工难度和施工成本，此时只要适当增大d即可不必增大hr而又能保证水平嵌岩桩的安全性。

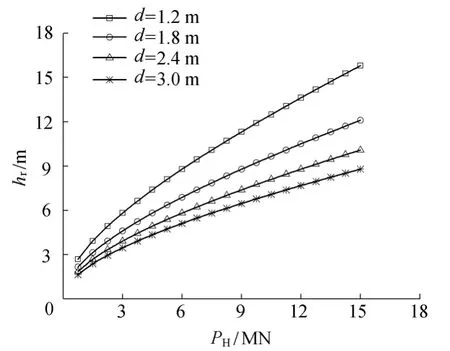
图4 hr-PH关系曲线

当 σc=4210 kPa，σt/σc=0.1，H= 1000 kN，上覆土层压应力σ3不同时，hr-d关系曲线如图5所示。由图5可知，hr随着d的增大而不断减小，随着σ3的增大而小幅度增大。这主要是因为增加d和上覆土层的厚度都会使嵌岩段桩侧抗力随之增大，从而使hr有所减小。当σ3=400 kPa时，d从1.2 m增大到3.0 m，而hr从3.91m只减小到2.37 m，这时要综合考虑实际工程中d、hr之间的合理关系，从而达到节约成本、减小施工难度的目的。此外当d=1.2 m，σ3从200 kPa增大到600 kPa时，hr仅仅从3.91 m减小到3.52m(约10%)。由此可见σ3对hr影响不大，这主要是由于σ3相对于桩侧岩石抗力较小，实际工程中为简化计算可不予考虑，作为一定的安全储备。

图5 hr-d关系曲线

4 结语

根据嵌岩桩嵌岩段受荷特性以及破坏机理，建立了嵌岩深度计算模型并得到最小嵌岩深度解析解。通过室内模型试验和现场设计数据对本文模型进行了验证，较其他方法，本文模型的计算结果与实测结果更为接近，证明其正确性。参数分析表明:嵌岩深度随着桩侧岩石单轴饱和抗压强度的增大而不断增大，但强度较大时嵌岩深度呈小幅递减趋势;嵌岩深度随着水平力的增大而增大，随着桩径的增大而减小，应结合现场实际情况综合考虑两者关系以尽量节约成本;上覆土层压应力对嵌岩深度影响较小，尤其是在土层厚度不大时，实际工程中为简化计算可不予考虑，作为一定的安全储备。

［1］史佩栋，梁晋渝．嵌岩桩竖向承载力的研究［J］．岩土工程学报，1994，16(4):32-38．(SHI Peidong，LIANG Jinyu．Vertical bearing capacity of rock-socketed piles［J］．Chinese Jounal of Geotechnical Engneering，1994，16(4):32-38．(in Chinese))

［2］劳伟康，周立运，王钊．大直径柔性钢管嵌岩桩水平承载力试验与理论分析［J］．岩石力学与工程学报，2004，23(10):1770-1777．(LAO Weikang，ZHOU Liyun，WANG Zhao．Field test and the oretical analysis on flexiblearge-diameter rock-socketed steel pipe piles under lateral load［J］．Chinese Journal of Rock Mechanics and Engineering，2004，23(10):1770-1777．(in Chinese))

［3］张志明，杨国平．在大水平力作用下嵌岩桩设计计算方法的探讨［J］．水运工程，2002(7):66-68．(ZHANG Zhiming，YANG Guoping．Research on design and calculation methods of rock socketed［J］．Port＆ Waterway Engineering，2002(7):66-68．(in Chinese))

［4］JTJ285—2000 港口工程嵌岩桩设计与施工规程［S］．

［5］JTGD63—2007 公路桥涵地基与基础设计规范［S］．

［6］汪荣麟．钻孔桩嵌岩深度计算的探讨［J］．公路，1981(6):11-13．(WANG Rongling．Discussion on calculation of the depth of the rock-socketed bored piles［J］．Highway，1981(6):11-13．(in Chinese))

［7］赵明华，张玲，刘建华．公路桥梁嵌岩桩嵌岩深度计算［J］．中 南 公 路 工 程，2007，32(1):1-3．(ZHAO Minghua，ZHANG Ling，LIU Jianhua．Calculation methods for socketed length of rock-socketed pile［J］．Journal of Central South Highway，2007，32(1):1-3．(in Chinese))

［8］牛双建，靖洪文，梁军起．不同加载路径下砂岩破坏模式试验研究［J］．岩石力学与工程学报，2011，30(2):3966-3974．(NIU Shuangjian，JING Hongwen，LIANG junqi．Experimental study of failure mode of sandstone under different loading paths［J］．Chinese Journal of Rock Mechanics and Engneering，2011，30(2):3966-3974．(in Chinese))

［9］ZHANG Lianyang，HELMUT T，HERBERT H E． Nonlinear analysis of laterally loaded rock-socketed shafts ［J］． Journal of Geotechnical and Geoenvironmental Engneering， 2000， 126( 11) : 995-998．

［10］王多垠，兰超，何光春，等．内河港口大直径嵌岩灌注桩横向承载性能室内模型试验研究［J］．岩土工程学报，2007，29(9):1307-1313．(WANG Duoyin，LAN Chao，HE Guangchun，et al．Researches on lateral support behavior of large diameter rock-socketed［J］．Chinese Journal of Geotechnical Engineering，2007，29(9):1307-1313．(in Chinese))

［11］周世良，李克森，关英俊．富宁港软岩桩基承载特性模型试验设计［J］．水运工程，2012(3):144-148．(ZHOU Shiliang，LI Kesen，GUAN Yingjun．Model test design of bearing characteristics of soft rock pile foundation in Funing port［J］．Port ＆ Waterway Engneering，2012(3):144-148．(in Chinese))

［12］关英俊．高原库区软岩嵌岩桩水平承载力性能研究［D］．重庆:重庆交通大学，2012．

［13］曹雪山． 水平荷载作用下的大口径嵌岩桩嵌固特性研 究［J］． 中国港湾建设， 1999( 4) : 14-16． ( CAO Xueshan． Studies on socketed character of a large-diameter rocksocketed pile under the action of horizontal loading［J］．China Harbour Engineering，1999 ( 4 ) : 14-16． ( in Chinese) )

［14］王建华，陈锦剑，柯学．水平荷载下大直径嵌岩桩的承载力特性研究［J］．岩土工程学报，2007，29(8):1194-1198．(WANG Jianhua，CHEN Jinjian，KE Xue．Characteristics of large diameter rock-socketed piles under lateralloads［J］．Chinese Journal of Geotechnical Engineering，2007，29(8):1194-1198．(in Chinese))

［15］刘佑荣，唐辉明．岩体力学［M］．武汉:中国地质大学出版社，1999．

［16］孙丽．论述岩石抗拉强度与单轴抗压强度两者之间的联系［J］．农林科技与信息，2012(14):48-49．(SUN Li．Discussesing the relationship between the uniaxial compressive strength and tensile strength of rock ［J］．Forestry Science and Technology and Information，2012(14):48-49．(in Chinese))