近50年来黄河入海水沙的多时间尺度特性分析

卢晓宁，洪 佳，王玲玲

（1.成都信息工程学院，成都610225；2.高原大气与环境四川省重点实验室，成都610225；3.数字制图与国土信息应用工程国家测绘地理信息局重点实验室（四川基地），成都610100）

黄河是以高泥沙含量为特征，黄河入海年均输沙量高达16亿万t［1］，这成为黄河三角洲重要的物质来源，也成为制约区域生态系统平衡的主要驱动力。随着区域人口增长、社会经济发展和水工程项目的建设，黄河的实测径流量和入海泥沙量发生了巨大变化，且在一定程度上造成黄河断流，并影响黄河输沙入海的连续性，进而严重影响海陆之间的相互作用及三角洲地带的环境变化和生态系统平衡［2］。众所周知，河流径流和入海输沙是联系陆地和海洋生态系统的重要纽带［3－4］。除中国的黄河以外，世界上还有许多河口及三角洲地带，比如埃及的尼罗河［5］、美国的佛罗里达河［6］等，它们的径流和入海输沙都受到自然和人类活动的干扰。径流和输沙量目前已经成为海洋与陆地交互作用带的研究热点。因此，研究黄河径流及其入海输沙不仅抓住当今世界的研究热点，也对黄河三角洲区域的生态系统平衡至关重要［7－8］。

目前已经开展了大量的关于黄河入海水沙的多时间尺度分析的研究，并得出了一些有价值的结论［9－14］。但是，在实时性和综合性方面仍存在一些问题。如刘峰等［12］只解释了黄河在2008年以前的径流及输沙的多时间尺度特征，且只对径流量和输沙量两方面进行了分析，而未讨论水沙系数的特征及规律。水沙系数表征的是单位流量的含沙量多少，可以揭示黄河某一时段河道以冲刷为主还是以淤积为主［15］。因此，本论文以黄河入海的主控测站利津站为代表站，从径流量、输沙量和水沙系数三个方面，应用复morlet连续小波变换这一广泛用于时间序列多时间尺度分析的方法［16－17］，探讨黄河入海水沙1964—2012年的多时间尺度特征，期望可以更加实时、更加综合地揭示黄河入海水沙的特征及规律，为维护黄河三角洲，尤其是河口区域的滨海湿地系统生态环境的稳定提供详实、可靠和及时有效的理论依据。

1 资料及方法

1.1 数据源及预处理

黄河发源于青海省巴颜喀拉山，流经青海、四川、甘肃、宁夏、内蒙古、山西、陕西、河南、山东9省（区），全长5 464km，流域面积752 443km2。黄河利津水文站为其入海水沙控制站。本文在获取得到黄河下游利津水文站1964—2012年（缺失1970年和1971年数据，采用滑动平均方法插补）共计49a的逐月径流量（亿m3）、逐月输沙量（亿t）和逐月平均输沙率（t／s）的基础之上，计算得到逐年总的径流量、总的输沙量，并用年均输沙量除以年均径流量得到年均水沙系数，该值越大则意味着单位流量含沙量大［15］。将以上处理的数据作为黄河入海水沙分析的基础数据，为避免量纲的不一致导致结果的不可比，对各时间序列数据进行标准化处理。因数据系列长度有限，为减少数据起端和终端受边界效应的影响，采用把数据反褶的方法对资料进行外延，得到长度分别为原序列3倍的数据序列，以此作为小波变换数据［18］，在小波变换完成后只提取中间的小波系数作为最终的小波变换结果。

1.2 小波变换方法

对于一维时间序列f（t）∈L2（R），小波变换Wf（a，b）的含义是把ψ（t）作位移b后，在不同尺度a下与待分析信号f（t）作内积［19－20］，其表达式如下：

1.2.1 小波变换函数 小波变换的关键是小波函数，这不仅是小波理论的重要内容，也是水文水资源时间序列分析的前提和条件［21］。复值小波的实部和虚部有π／2的位相差，可以消除实数形式的小波变换系数模的振荡，分离出小波变换系数的模和位相，前者给出能量密度，从后者中则可发现信号的奇异性和瞬时频率［22］。文中采用复值 Morlet小波对年水沙序列进行分析，复值Morlet小波是高斯包络下的单频率复正弦函数，表示为：

式中：c为常数；i表示虚部。

1.2.2 小波变换结果制图

（1）复值Morlet小波变换结果的模的平方时频结构图。由小波变换理论可知［19，23］，小波变换模部的平方，同函数f（t）在其小波变换域中能量的大小成正比。因此，为分析方便和直观，把反映黄河入海水沙在小波变化域中波动的能量曲面，以等值线的形式投影到以尺度a为纵坐标，时移b为横坐标的（a，b）平面上，等值线上的每一点值，都对应于曲面上点的值，而曲面上能量集中的顶点是其极值点，它在（a，b）平面上的投影为一点，此点称为能量中心点，其强弱用小波变换系数Wf（a，b）模部的平方值来反映。图1—3即为黄河入海年径流、输沙量和水沙系数时间序列的复值Morlet连续小波变换的模的平方的等值线图，以此图来分析黄河入海水沙在小波变化域中波动能量强弱的变化特性，进而反映哪些能量聚集中心主导入海水沙在时间域上的波动变化。

（2）复值Morlet小波变换结果的实部时频结构图。同样由小波变换理论可知［19，23］，函数f（t）在小波变化域中的波动特性是用小波变换系数Wf（a，b）实部变化来刻画。类似小波变换系数模的平方能量曲面的处理方法，将小波变换系数实部的能量曲面转换成小波变换系数实部的等值线图，等值线上的每一点值，都对应于波动曲面上点的值，其大小用小波变换系数Wf（a，b）的实部值来反映。小波变换系数的实部表示不同特征时间尺度信号在不同时间上的分布与位相两方面的信息，若实部为正，表示偏多；为负则表示偏少；为零处，则对应于变化的突变点。

2 结果与分析

2.1 小波变换系数模的平方及多时间尺度特性分析

2.1.1 黄河入海年径流序列的模的平方及多尺度特性 模平方等值线图即为能量图（图1），从中可以分析黄河入海年径流量在小波变化域中波动能量强弱的变化特性，进而反映哪些能量聚集中心主导年径流在时间域上的波动变化［21］。由图1小波模值的平方的极值大小可以判定，黄河入海年径流序列主要存在3个能量聚集中心，它们分别是2～6a尺度、＞40a尺度和15～25a尺度，且以2～6a尺度的能量极值最高，尺度中心在4a左右，小波变换系数模值的平方在该时间尺度上的最高值达到3.80，但该尺度上振荡涉及的时域范围较窄，主要集中在1965—1975年。＞40a尺度的周期振荡的能量虽不是最高，但也相当强，能量中心的极值高达2.5，尺度的中心在47a左右，且该尺度上的周期振荡具有全域性，即1965—2012年的整个时间序列上，黄河入海年径流都存在较强的以45a尺度为周期的较强的能量振荡变化；15～25a尺度的能量波动较低，能量中心的极值仅达到1.8，尺度中心在23a左右，但该尺度上的能量振荡不具有全域性，振荡范围主要在1965—1990年的时域范围内，且在1965—1980年能量振荡更为突出。此外，还存在一个相对较弱的，以8a为尺度中心的，5～10a的能量振荡中心，但该振荡中心的能量极值只达到0.6，尺度中心在8a左右，振荡的中心在1981年左右，虽然该尺度的周期较弱，但在时域上影响的范围要较2～6a尺度的广，在1975—2000年这一较广的时域上都有体现。由此可见，黄河入海径流量在整个时域范围内，主要存在大于40a尺度的周期振荡，不同时间尺度下周期信号的强弱在时—频域中的分布具有较强的局部特征，这可能是由于影响径流演变的因子，如气候系统（降雨、蒸发）、下垫面（地貌、土壤和植被）和人类活动的耦合作用在不同阶段信号作用的强弱不同所致［22，26］。

图1 黄河入海年径流序列小波变换系数的模的平方时频结构

2.1.2 黄河入海年输沙量序列的模的平方及多尺度特性 由黄河入海输沙的小波变换系数模值的平方图（图2）可以发现，相对于年入海径流量，黄河的年入海输沙量的周期性波动特性不是非常显著，小波变换系数模值的平方的最大值仅为1.68，该能量强度仅仅达到年入海径流量的26.82%，且只存在两个相对较高的能量聚集中心，分别是＞36a尺度和2～5a尺度的能量波动中心，且以2～5a尺度的能量波动最强，尺度中心在4a左右，这一尺度的能量振荡涉及的时域范围很窄，只从1964年始，影响到1973年；＞36a尺度的能量波动虽然相对较弱，尺度中心在45a左右，中心极值只达到1.53，但涉及的时间尺度最长，体现出一定的全域性，只是该时间尺度上的能量振荡具有随时间推移尺度下降的变化。此外，还存在一个5～10a，以7a左右为尺度中心，和13～20a，以14a左右为尺度中心的两个弱的能量积聚的中心，虽然这两个能量集聚区的中心值很低，极值分别只达到0.55和0.65，但就其影响的时域广度而言，该两个尺度的作用要更为突出，14a尺度的能量振荡的时域范围最广，从1964年始，至2004年结束；7a尺度能量波动影响的时域范围亦从1964年开始，一直持续到1995年。除以上表述的4个能量积聚中心外，黄河年输沙序列还存在在整个时域上零散分布的能量集聚中心，但中心值普遍很低，以局域性特征显著。

图2 黄河入海年输沙量序列的小波变换系数模的平方时频结构

2.1.3 黄河入海年均水沙系数序列的模的平方及多尺度特性 由图3可以看出，与黄河入海年径流及年输沙的周期波动强度相比，黄河入海的年均水沙系数的周期性波动能量最强，小波变换系数模值的平方的极值达到6.25，分别是年入海径流量及年输沙量的小波变换系数模值平方极值的1.65倍和3.73倍。就能量聚集中心的数量上看，黄河入海年均水沙系数主要存在两个能量积聚中心，分别为28～47a尺度和10～23a尺度，两个时间尺度的能量波动都体现为一定的全域性，只是28～47a尺度的能量波动随时间推移有加强的趋势，尺度中心位于33a左右，1990年以后，这一时间尺度的能量更强，能量中心的极值高达5.98，这一能量强度远远超过黄河入海径流和入海输沙量在这一尺度上的能量强度，这在一定程度上可以说明大于30a尺度的年代际周期变化以黄河入海水沙系数的表现最为强烈。10～23a时间尺度的能量震动相对较弱，中心尺度在18a左右，其能量中心的极值达到3.09，虽然这一时间尺度的能量波动具有一定的全域性，但是能量振荡的主要时域范围是1984—2005年，从该时域的始和末向前和向后，都呈现出波动能量减弱的变化。

2.2 小波变换系数实部及多尺度特性分析

2.2.1 黄河入海年径流量序列的实部及多尺度特性 由于选定的基准面是以黄河入海年径流（年输沙量／年均水沙系数）的多年平均值为代表的平面，则Wf（a，b）的实部（包括极值点）在（a，b）平面等值线上的正或负的量值，表示黄河入海水沙序列在小波变化域中以多年平均值为基准面上下起伏的波动情况，进而反映黄河入海年径流量（年输沙量／年均水沙系数）在时间域上丰（多／强）或枯（少／弱）变化的特性。以径流的分析为例，小波系数为正，表示径流量偏多的丰水期；为负则代表径流量偏少的枯水期。由小波系数实部的时频分布图（图4—6），可得到不同时间尺度下的年径流量丰枯位相结构，展示不同时间尺度所对应的黄河入海年径流量的丰枯交替变化特征及突变点的位置。

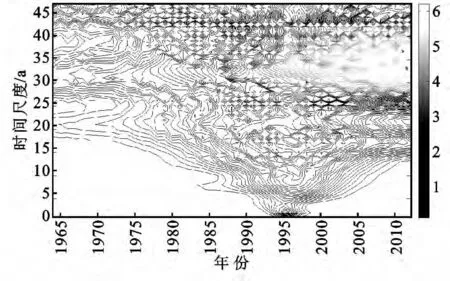
图3 黄河入海年均水沙系数的小波变换系数模的平方时频结构

由图4可看出，黄河入海年径流序列存在明显的周期性变化特征，且不同时间尺度上周期性的强弱及其影响的时域范围不一致。其中，＞45a，23a和4a年左右尺度的丰、枯交替变化表现较清晰，波动极值点分布的规律性显著。＞45a尺度的年代际周期信号很强，小波系数等值线闭合值高，说明该时间尺度下径流的丰枯交替显著，突变特征明显，这也可以通过小波系数模值的平方具有很高的值得以体现，表明黄河年径流量在这一时间尺度上丰水年呈远远高于多年平均值的特征，而枯水年又表现出远远低于多年平均值的特征（图5），且以该时间尺度为周期的年径流的剧烈的丰枯交替变化具有全域性特征，黄河入海年径流在这一尺度上呈现出丰、枯、丰的明显的交替振荡，丰枯变化的具体时段参见表1。由表1可知，黄河入海径流目前处于高于多年平均值的丰水期，且呈现出显著的增长趋势；23a尺度的年代际周期变化的能量亦强，但不具有全域性，周期振荡突出表现在1964—1990年，黄河入海径流在该尺度上呈丰、枯、丰交替变化；4a尺度的年际周期变化能量最强，小波系数实部等值线分布最密集，但该尺度上年径流丰枯波动的局域性特征更突出，主要集中在1964—1972年，黄河入海径流在该时域范围内呈丰、枯、丰的交替振荡，是23a尺度丰水期下的更小尺度的丰枯变化；8a尺度的年际周期变化能量虽然不强，但其影响的时域范围较4a尺度的更深远，表现为从1973年开始即进入以8a为周期的年径流枯、丰交替变化，且一直持续到1990年。

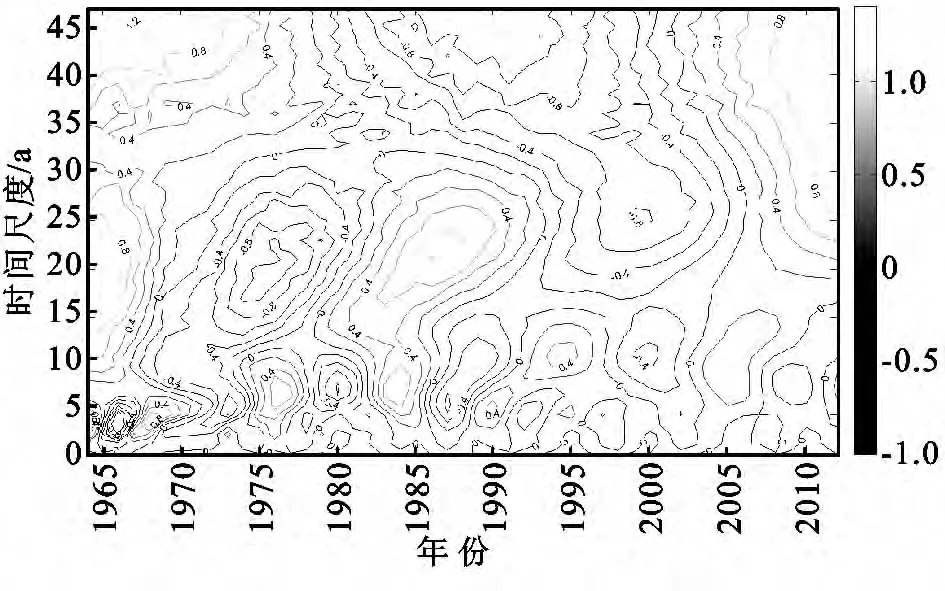
图4 黄河入海径流序列小波变换实部时频结构

2.2.2 基于实部的黄河入海年输沙量序列的多尺度特性 由图6可以看出，黄河入海年输沙量周期性变化的规律性不及年径流的强，主要存在具有全域性的大于36a尺度的年代际周期性变化，但该时间尺度上的尺度中心不明显，且小波系数实部等值线的嵌套结构不明显，即能量波动的规律性不强，能量波动极值点在整个时域范围内呈散乱分布，这说明在该尺度上，虽然黄河入海输沙亦呈现出多与少的交替变化，但多与少的交替变化强度不及年径流量，表现在同一个多沙期或少沙期内，黄河入海的输沙量都呈现出明显的波动变化，这可通过该序列小波变换实部随时移的变化图（图7）得以体现。就局部能量波动的强弱上来看，以2～5a的年际周期变化最为强烈，表现为该时间尺度上小波变换系数的实部等值线密集，以4 a为尺度中心的能量极值高达1.26，但在时域上只突出表现在1964—1973年，该时域范围内黄河入海输沙呈现出以1965年、1967年、1971年为突变年的多、少、多、少的交替变化，且随时间推移，该尺度上的多与少的振荡强度明显减弱（图7）。在整个时域上突出体现出来的是能量并不高，但能量振荡的时域范围较广，且具有一定的全域性，以14a左右为尺度中心的年代际周期变化和以7a为尺度中心的年际周期变化，随着时间推移，黄河年入海输沙量的所表现出的7a和14a左右的周期变化的强度亦在逐渐减弱（图7）。

图5 不同尺度的黄河入海年径流小波变换系数实部变化曲线

表1 不同时间尺度黄河入海年径流的演变特征

因此，总体来说，能量最强的4a左右时间尺度的年际周期性变化对黄河年入海输沙量的影响体现出很强的局域性，表现在全域上的是大于36a尺度的年代际周期变化，但周期性的强度不及4a尺度，且丰枯中心不明显；7a及14a左右的周期性变化亦具有全域性，但周期振荡能量相对较弱，且随时间推移，表现出尺度降低的变化趋势。

他们只管自己细声谈笑。她是内地学校出身，虽然广州开商埠最早，并不像香港的书院注重英文。她不得不说英语的时候总是声音极低。这印度老板见言语不大通，把生意经都免了。三言两语讲妥价钱，十一根大条子，明天送来，份量不足照补，多了找还。

2.2.3 基于实部的黄河入海年水沙系数序列的多尺度特性 由图8可以清晰地看出黄河入海年均水沙系数序列所存在的两个年代际周期波动，它们分别是以33a为尺度中心的28～47a尺度的年代际周期变化，和以18a为尺度中心的10～23a尺度的年代际周期变化。33a尺度的年代际周期变化最强，表现为小波变化系数实部的等值线更为密集，且越随时间推移，这一能量波动的周期性加强，使得黄河入海水沙系数在整个研究时期内呈现出高—低—高—低的周期性变化。18a尺度的年代际周期变化能量相对较弱，表现为小波变换系数的实部等值线变疏，且这一尺度的能量波动也主要体现在1990年以后，黄河入海水沙系数在整个研究时期内在这一尺度上呈现出低—高—低—高—低—高的周期性波动（图9，表2）。

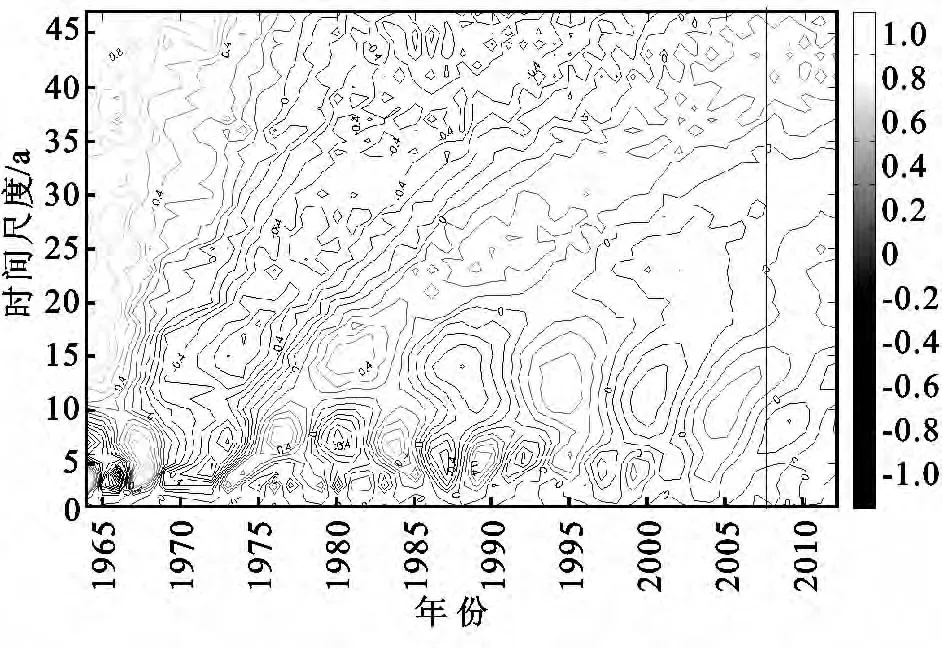
图6 黄河入海输沙的小波变换系数实部时频结构

图7 不同尺度的黄河入海输沙量的小波系数实部变化曲线

2.3 水沙径流序列小波方差检验

将时间域上的不同尺度a的所有小波系数的平方进行积分，即为小波方差［17－18］：

小波方差检验可以确定一定时间系列中存在的主要时间尺度，即对径流序列的演变起主要作用的周期。利用小波方差的定义，计算黄河入海水沙距平序列的小波方差，绘制小波方差图（图10），它反映了水文序列中所包含的各种尺度的波动及其强弱随尺度变化的特性。

图8 黄河入海水沙系数的小波变换系数实部时频结构图

图9 不同时间尺度的黄河入海水沙系数小波变化实部

由图10a可以看出，黄河入海径流序列主要存在三个尺度的周期振荡：就整个时间序列上看，以＞40a尺度的年代际周期波动最为强烈，表现为＞40a的小波方差持续增长，且到研究时段末期都未达到峰值，极大值已经达到71.10；此外，还存在一个以23a左右为中心的年代际周期振荡，但该尺度上的能量振荡不强，且不具有全域性特征，这一点与图1和图4的表现一致，该尺度上小波方差峰值仅为23，仅及＞40a尺度小波方差极值的48.94%；4a尺度为中心的年际周期变化亦较强，小波方差峰值达到16.76，虽然它在整个时间段上的周期性并不显著，但在短时间范围内该时间尺度上周期性振荡非常突出，与前面分析一致。

表2 不同时间尺度黄河入海年均水沙系数的演变特征

图10 黄河利津站水沙序列小波方差

由图10b可知，黄河入海年输沙量以大于36a尺度的年代际周期变化最为突出，表现为该尺度上的小波方差值最高，47a尺度上的小波方差值已经达到22.30，且随着时间推移呈现出明显的小波方差值显著增长的变化，这说明年输沙量随时间推移存在尺度增长的变化；以4a尺度为中心的年际周期振荡亦较强，小波方差峰值达到11.70，但该尺度的周期振荡主要体现在1970年以前；除此之外，还存在一个以14a尺度为中心的周期性振荡，该尺度上的小波方差峰值达到10.58；以7a为尺度中心的年际周期性振荡亦较为突出，小波方差峰值为9.43，该尺度上的小波方差值虽然较小，但是在整个时间尺度上的表现要较4a尺度为中心的年际周期振荡强，其影响的年限从研究初期开始一直持续到2000年。

由图10c可知，黄河年均水沙系数主要存在两个尺度上的周期性振荡，且周期性振荡的强度要远远高于年径流和年输沙是以33a和18a为尺度中心的年代际周期振荡。以33a为中心的年代际周期振荡的小波方差值高达到148.00，这一点与年均水沙系数的时频结果图表现一致。以18a为尺度中心的年代际周期振荡虽然不及33a的强，但其小波方差也达到了68.78，与年径流的小波方差最大值已很接近，而且超过了年输沙的小波方差极值。

3 结 论

本研究以Matlab为平台，选择复值Morlet小波为母函数，对黄河入海的控制测站——利津站自1964—2012年的水沙序列，包括年径流量、年输沙量和年均水沙系数序列进行了多时间尺度特性分析，实现了黄河水沙径流分析的实时性、全面性和有效性。本研究所得主要结论如下：

（1）1964—2012年，黄河入海水沙序列都存在明显的多时间尺度特性，且这种多时间尺度特性以年均水沙系数的周期性表现最为突出，其次为年径流，再次为年输沙。

（2）黄河入海年均水沙系数主要存在两个具有全域性的年代际尺度上的周期性振荡，以33a为尺度中心的主周期性振荡最强，导致黄河入海水沙系数在整个研究时域范围内呈现出以1976年、1987年和2005年为突变年的高、低、高、低的周期性振荡；以18a为尺度中心的次周期的强度都超过了年输沙的主周期的强度，导致黄河入海水沙在该尺度上呈现出以1972年、1982年、1992年、2001年和2010年为突变年的低、高、低、高、低、高的周期性振荡。

（3）黄河入海年径流量主要存在三个尺度上的周期性振荡，以具有全域性的大于45a的年代际周期性振荡最强，使得黄河入海径流在整个时域范围内呈以1978年和1988年为突变年的丰、枯、丰的交替振荡，且随时间推移表现出尺度增长的趋势；以23a为尺度中心的年代际周期振荡的能量虽不是最强，但具有一定全域性，导致黄河年径流在整个研究时域范围内以1969年、1981年为突变点的丰、枯、丰的交替振荡；以4a为尺度中心的年际周期振荡虽不是最显著，只具有局域性，但其振荡的能量最强，导致黄河年径流在1964—1972年呈现出以1965年和1967年为突变点的丰、枯、丰的交替振荡，且振荡最为剧烈。

（4）黄河入海输沙序列的多尺度特性最不显著，主要存在大于36a尺度的年代际周期变化，且随时间推移表现出明显的尺度增长趋势；以4a尺度为中心的年际周期性振荡虽然局域内能量非常强，但只影响1970年以前的时域；整个时间序列上还存在以14a尺度为中心的振荡能量相对较弱的年代际周期变化。

（5）虽然黄河年径流量和输沙量目前处于高于多年平均值的高值期，且随时间推移二者都呈增长变化，但年均水沙系数却表现出低于多年平均值的低值期，且随时间推移具有显著减小的变化趋势，说明黄河河道目前处于次饱和状态的冲刷作用为主，且未来有加强的趋势。

［1］ 秦蕴珊.渤海地质［M］.北京：科学出版社，1985.

［2］ 许炯心.流域因素与人类活动对黄河下游河道输沙功能的影响［J］.中国科学：D辑，2004，34（8）：775－781.

［3］ Walling D E.Human impact on land－ocean sediment transfer by the world′s rivers［J］.Geomorphlogy，2006，79（3／4）：192－216.

［4］ Milliman J D，Farnsworth K L，Jones P D，et al.Climatic and anthropogenic factors affecting river discharge to the global ocean，1951—2000［J］.Global and Planetary Change，2008，62（3／4）：187－194.

［5］ Fanos A M.The impacts of human activities on the erosion and accretion of the Nile Delta coast［J］.Journal of Coastal Research，1995，11（3）：821－833.

［6］ Carriquiry J D，Sanchez A.Sedimentation in the Colorado River Delta and upper gulf of California after nearly a century of discharge loss［J］.Marine Geology，1999，158（1／4）：125－145.

［7］ Syvitski J P M，Vorosmarty C J，Kettner A J，et al.Impact of humans on the flux of terrestrial sediment to the global coastal ocean［J］.Science，2005，308（5720）：376－380.

［8］ Yang S L，Shi Z，Zhao H Y，et al.Effects of human activities on the Yangtze River suspended sediment flux into the estuary in the last century［J］.Hydrology and Earth System Sciences，2004，（8）：1210－1216.

［9］ 胡春宏，张治吴.水沙过程变异条件下黄河口拦门沙的演变响应与调控［J］.水利学报，2006，37（5）：511－524.

［10］ Wang H J，Bi N S，Satio Yoshiki，et al.Recent changes in sediment delivery by the Huanghe（Yellow River）to the sea causes and environmental implications in its estuary［J］.Journal of Hydrology，2010，391（3／4）：302－313.

［11］ Peng Jun，Chen Shenliang，Dong Ping.Temporal variation of sediment load in the Yellow River Basin，China，and its impacts on the lower reaches and the river delta［J］.Catena，2010，83（2／3）：135－147.

［12］ 刘锋，陈沈良，彭俊，等.近60a黄河入海水沙多尺度变化及其对河口的影响［J］.地理学报，2011，66（3）：313－323.

［13］ 蒋晓辉，刘昌明，黄强.黄河上中游天然径流多时间尺度变化及动因分析［J］.自然资源学报，2003，18（2）：142－147.

［14］ 孙卫国，程炳岩，李荣.黄河源区径流量与区域气候变化的多时间尺度相关［J］.地理学报，2009，64（1）：117－127.

［15］ 吴保生，申冠卿.来沙系数物理意义的探讨［J］.人民黄河，2008，30（4）：15－16.

［16］ 丁文容，周跃.云南省盘龙河流域输沙率变化的多时间尺度分析［J］.水土保持研究，2007，14（6）：278－279.

［17］ 张月丛，张才玉，成福伟，等.承德市近58a气温和降水序列多时间尺度分析［J］.水土保持研究，2012，19（5）：70－73.

［18］ 林振山，邓子旺.子波气候诊断技术的研究［M］.北京：气象出版社，1991.

［19］ 彭玉华.小波变换与工程应用［M］.北京：科学出版社，2002.

［20］ 冉启文.小波变换与分数傅里叶变换理论应用［M］.哈尔滨：哈尔滨工业大学出版社，2001.

［21］ 王文圣，丁晶，向红莲.水文时间序列多时间尺度分析的小波变换法［J］.四川大学学报：工程科学版，2002，34（6）：14－17.

［22］ 姚棣荣，钱恺.小波变换在新安江流域近百年降水变化分析中的应用［J］.科技通报，2001，17（3）：17－21.

［23］ 刘会玉，林振山，张明阳.建国以来中国洪涝灾害成灾面积变化的小波分析［J］.地理科学，2005，25（1）：43－44.

［24］ 胡昌华，张军波.基于Matlab的系统分析与设计：小波分析［M］.西安：西安电子科技大学出版社，1999.

［25］ 杨福生.小波变换的工程分析与应用［J］.北京：科学出版社，2001.

［26］ 卢晓宁，邓伟，张树清，等.霍林河中游径流量序列的多时间尺度特征及其效应分析［J］.自然资源学报，2006，21（5）：819－826.