应用灰色关联度分析法对不同地区粳稻种质资源农艺性状分析评价*

罗雅兰，戴红燕，丁 鑫，郭长春，马 瑞，李吉进，毛庭德，华劲松

（西昌学院，四川 西昌 615013）

应用灰色关联度分析法对不同地区粳稻种质资源农艺性状分析评价*

罗雅兰，戴红燕**，丁 鑫，郭长春，马 瑞，李吉进，毛庭德，华劲松

（西昌学院，四川 西昌 615013）

为了解不同地区粳稻资源的性状差异，并为新品种选育提供亲本材料，将来自中国云南、四川凉山州和日本的部分粳稻种质资源进行同田比较。通过对多个性状数据的测定比较，应用灰色关联度分析法分析，综合评价各品种资源性状。研究结果表明：不同地区间的品种资源性状各有差异，各品种性状优缺点共存，产量性状好的关联度排名较后，而关联度排名靠前的产量又较低，其中Y5和B130可以通过栽培技术的改进来提高产量，也可作为育种的亲本材料。

粳稻资源；农艺性状；灰色关联度分析法

随着农业科技的发展，选育的水稻新品种在产量上越来越高，但品种间的遗传基础却越来越窄，其新品种的抗性可能无法应对突如其来的灾害而导致严重的减产，因此，拓宽水稻新品种的遗传基础，培育遗传背景多样的高产优质品种，对水稻生产的可持续发展有重要作用。

灰色关联度分析法是以各因素的样本数据为依据，描述因素间关系的强弱、大小和次序[1]。近年来，灰色系统理论已越来越多地应用于作物新品种综合评价[2],但在粳稻资源评价方面却报道甚少。因此，我们收集了日本、中国四川凉山州和云南省的部分粳稻品种资源，开展了品种观察试验，应用灰色关联度分析法对品种的农艺性状数据进行分析并对其进行评价，选出综合性状良好的资源进行改良，为新品种选育提供亲本材料。

1 材料与方法

1.1 试验材料

凉山州地方品种B130、B132、X32等3个品种，云南引进粳稻品种B112、B111、B114、B118、B121、B113、B119、B124、B126、B127、B116等11个品种，日本粳稻品种Y8、Y48、Y26、Y27、Y25、Y5、B41、B31、B40、B27、B37、B35、X6、X5、X24、X26、X22、X25等18个品种（我们将代号统一为H，即凉山品种为H1～H3，云南品种为H4～H14，日本品种为H15～H32，H0为理想品种）。

1.2 试验方法

试验田设在西昌学院试验农场，四周无荫蔽，排灌条件良好，土质为壤土，肥力适中。2014年3月 29日播种，秧盘育秧，5月9日移栽，每品种种植20穴，每穴3苗，移栽规格为20 cm×13.5 cm。试验期间每项管理措施在同一天内完成且均匀一致，治虫治草不治病，成熟一个品种收割一个。

移栽成活后开始调查测定性状数据，每品种固定10穴，每隔10 d测定一次。成熟后，收割前每品种取4穴进行室内考种。

1.3 测定性状

包括全生育期、株高、株型、叶色、叶型、分蘖苗数、剑叶和倒二叶性状、茎秆长度、茎秆粗细、有效穗、穗长、穗实粒数、千粒重、结实率、抗病性、抗倒性、产量、稻谷颜色、芒色等。然后选取数量性状数据和部分质量数据，应用灰色关联度分析法对各品种进行分析评价。其中，病害抗性分为抗病、轻感、中感、重感四个等级进行评定。

1.4 分析步骤

参照华劲松[3]的分析步骤，首先确定参考序列，然后确定比较序列，再计算关联系数，最后计算关联度。

2 试验结果

2.1 理想品种的确定

首先根据育种目标和经验给出理想品种农艺性状的最佳值，构成一个参考序列X0(k),k=1，2，3，...，13。各参试品种的主要性状表1所示，其中抗病性分为抗病、轻感、中感、重感四个等级并分别赋值4、3、2、1，株型分为紧凑、半紧凑、披散三个等级并分别赋值3、2、1，糙米颜色分为有色和无色2个等级并分别赋值2、1，稻谷的芒分为无芒和有芒2个等级并分别赋值2、1。

表1 参试品种与理想品种的主要性状值

2.2 数据的无量纲化处理

将Xi(k)所有除以相应的X0（k），i=0，1，2，...，32，k=1,2,3，...，13，使原始数据无量纲化得表2。

表2 原始数据无量化处理后的表

X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X17 X18 X19 X20 X21 X22 X23 X24 X25 X26 X27 X28 X29 X30 X31 X32 0.8035 1.1440 0.9855 0.8965 0.7070 1.1560 0.7725 0.7455 0.8940 0.6550 0.9415 0.9180 0.8965 0.7468 1.0015 0.8170 0.8250 0.9400 0.8400 0.8125 0.9855 0.0742 1.0165 0.8580 1.1375 0.8900 0.9920 0.9600 1.0240 1.0000 0.8400 0.8480 0.8960 0.8560 0.8240 0.8000 0.9000 0.9000 0.9000 0.9920 1.0000 0.9920 1.0000 0.8240 1.0160 1.0080 0.8160 0.9600 1.0240 0.9440 0.9120 0.9200 0.9938 0.9563 1.0313 1.0250 1.0625 1.1111 1.0563 1.0438 0.8625 0.9375 0.9675 0.9200 0.9300 0.8125 0.7613 0.7870 0.8499 0.8634 0.7084 0.6178 0.7390 0.7518 0.8563 0.9654 0.7666 0.9516 1.1259 1.2741 0.9719 1.3296 0.7830 1.0778 0.7141 0.7778 0.9696 1.1185 0.8867 0.7296 1.1378 1.1607 1.0904 0.9844 0.8311 1.0459 0.8533 0.9459 0.8659 0.5663 0.8978 0.8385 0.9081 0.8148 0.8110 1.4000 0.8580 0.9540 0.8090 1.3305 0.7750 0.9490 0.8180 0.7550 1.2930 0.8900 0.9550 0.9520 0.7675 0.5975 1.0300 1.0975 0.7300 0.7050 0.9870 0.6750 1.0000 0.9775 0.9330 1.0600 0.8267 0.6400 0.7067 0.7200 0.8933 1.1733 0.7200 0.7467 0.8000 0.9067 0.6933 0.7467 1.0400 1.1467 0.8400 101867 0.7467 0.8933 0.8667 0.9600 0.9200 1.4400 1.0800 0.9333 0.9867 1.2533 1.0195 0.8317 0.8058 1.0903 0.6936 1.3239 0.5406 0.5765 0.6125 0.8451 0.5948 0.5012 1.1005 1.1920 0.7747 1.0134 0.5860 0.7386 0.5914 0.6283 0.5338 0.6539 0.9446 0.7925 0.6961 0.9934 1.0000 0.5000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.5000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.5000 0.5000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.7500 0.7500 0.7500 0.7500 0.7500 0.7500 1.0000 0.7500 0.7500 1.0000 0.7500 0.7500 1.0000 0.7500 0.7500 0.7500 1.0000 0.5000 0.7500 1.0000 0.7500 0.7500 0.7500 0.7500 0.7500 0.3333 1.0000 0.3333 0.6667 0.6667 1.0000 1.0000 1.0000 0.6667 0.6667 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.6667 1.0000 0.6667 1.0000 1.0000 1.0000 0.3333 0.5000 1.0000 0.5000 1.0000 1.0000 1.0000 0.5000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.5000 0.5000 0.5000 1.0000 0.5000 0.5000 0.5000 1.0000 1.0000 1.0000 0.5000 1.0000 1.0338 1.0541 1.0946 1.0676 1.0743 1.0676 1.0868 1.0868 1.0473 1.0676 1.0676 1.0608 1.0608 1.0608 1.0676 1.0608 1.0541 1.0811 1.0811 1.0811 1.0811 1.0676 1.0676 1.0676 1.0676 1.0608 0.6667 1.0000 0.6667 0.6667 0.3333 1.0000 1.0000 0.6667 0.6667 0.6667 0.6667 1.0000 1.0000 1.0000 0.3333 1.0000 1.0000 0.6667 0.3333 0.3333 0.6667 0.3333 0.6667 1.0000 1.0000 0.6667

.3求两个层次差

即计算Δi(k)的值，公式为Δi=|X0(k)-Xi(k)|，i=0，1，2，...32，k=1,2,3，...，13。结果列于表3。

表3 各参试品系与理想品种性状的绝对差值

△18△19△20△21△22△23△24△25△26△27△28△29△30△31△32 0.0820 0.1035 0.2535 0.0015 0.1830 0.1750 0.0600 0.1600 0.1875 0.0145 0.9259 0.0165 0.1420 0.1375 0.1100 0.1000 0.1000 0.0080 0.0000 0.0080 0.0000 0.1760 0.0160 0.0080 0.1840 0.0400 0.0240 0.0560 0.0880 0.0800 0.0800 0.0700 0.1875 0.2388 0.2130 0.1501 0.1366 0.2916 0.3823 0.2610 0.2483 0.1438 0.0346 0.2334 0.0484 0.2704 0.1378 0.1607 0.0904 0.0156 0.1689 0.0459 0.1467 0.0541 0.1341 0.4337 0.1022 0.1615 0.0919 0.1852 0.1100 0.0450 0.0480 0.2325 0.4025 0.0300 0.0975 0.2700 0.2950 0.0130 0.3250 0.0000 0.0225 0.0670 0.0600 0.2533 0.0400 0.1467 0.1600 0.1867 0.2533 0.1067 0.1333 0.0400 0.0800 0.4400 0.0800 0.0667 0.0133 0.2533 0.4988 0.1005 0.1920 0.2253 0.0134 0.4140 0.2614 0.4086 0.3717 0.4662 0.3461 0.0554 0.2075 0.3039 0.0066 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.5000 0.5000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.2500 0.2500 0.0000 0.2500 0.2500 0.2500 0.0000 0.5000 0.2500 0.0000 0.2500 0.2500 0.2500 0.2500 0.2500 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.3333 0.0000 0.3333 0.0000 0.0000 0.0000 0.6667 0.0000 0.0000 0.0000 0.5000 0.5000 0.5000 0.0000 0.5000 0.5000 0.5000 0.0000 0.0000 0.0000 0.5000 0.0000 0.0608 0.0608 0.0608 0.0676 0.0608 0.0541 0.0811 0.0811 0.0811 0.0811 0.0676 0.0676 0.0676 0.0608 0.0608 0.0000 0.0000 0.0000 0.6667 0.0000 0.0000 0.3333 0.6667 0.6667 0.3333 0.6667 0.3333 0.0000 0.0000 0.3333

2.4 求比较品种与理想品种的关联系数

最小二级差min|X0(k)-Xi(k)|为0.0000，最大二级差max|X0(k)-Xi(k)|为0.9744，分辨系数取0.5，把然后带入公式带入公式：

式中：￡(k)为X0与Xi在第k个指标的关联系数：|X0(k)-Xi(k)|表示数列与数列在第点的绝对值差，min|X0(k)-Xi(k)|为二级最小差，max|X0(k)-Xi(k)|为二级最大差。p为分辨率。结果列于表4。

表4 各参试品种的关联系数

￡21￡22￡23￡24￡25￡26￡27￡28￡29￡30￡31￡32 0.9969 0.7270 0.7357 0.8904 0.7528 0.7221 0.9711 0.3448 0.9672 0.7743 0.7799 0.8158 1.0000 0.9838 1.0000 0.7346 0.9682 0.9838 0.7259 0.9241 0.9531 0.8969 0.8470 0.8590 0.6711 0.6958 0.7645 0.7810 0.6256 0.5604 0.6512 0.6625 0.7722 0.9336 0.6761 0.9097 0.8435 0.9691 0.7426 0.9139 0.7686 0.9001 0.7842 0.5291 0.8266 0.7511 0.8414 0.7246 0.6770 0.5476 0.9420 0.8333 0.6434 0.6229 0.9740 05999 1.0000 0.9559 0.8791 0.8904 0.7528 0.7230 0.6579 0.8204 0.7851 0.9241 0.8590 0.5255 0.8590 0.8796 0.9734 0.6579 0.6838 0.9733 0.5406 0.6508 0.5439 0.5672 0.5110 0.5847 0.8979 0.7013 0.6158 0.9867 1.0000 1.0000 1.0000 1.0000 0.4935 0.4935 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.6609 0.6609 0.6609 1.0000 0.4935 0.6609 1.0000 0.6609 0.6609 0.6609 0.6609 0.6609 1.0000 1.0000 1.0000 1.0000 1.0000 0.5938 1.0000 0.5938 1.0000 1.0000 1.0000 0.4222 0.4935 0.4935 0.4935 1.0000 0.4935 0.4935 0.4935 1.0000 1.0000 1.0000 0.4935 1.0000 0.8782 0.8890 0.9001 0.8573 0.8573 0.8573 0.8573 0.8782 0.8782 0.8782 0.8890 0.8890 0.2276 0.3304 0.3304 0.2695 0.2276 0.2276 0.2695 0.2276 0.2695 0.3304 0.3304 0.2695

2.5 求关联度及关联度排序结果

式中：ri为比较数列Hi对参考数列H0的关联度，是总体反应H0与Hi数列之间的关联性。

然后计算出各参试品种的一般关联度和地方品种平均关联度，并排出关联序，见表5。

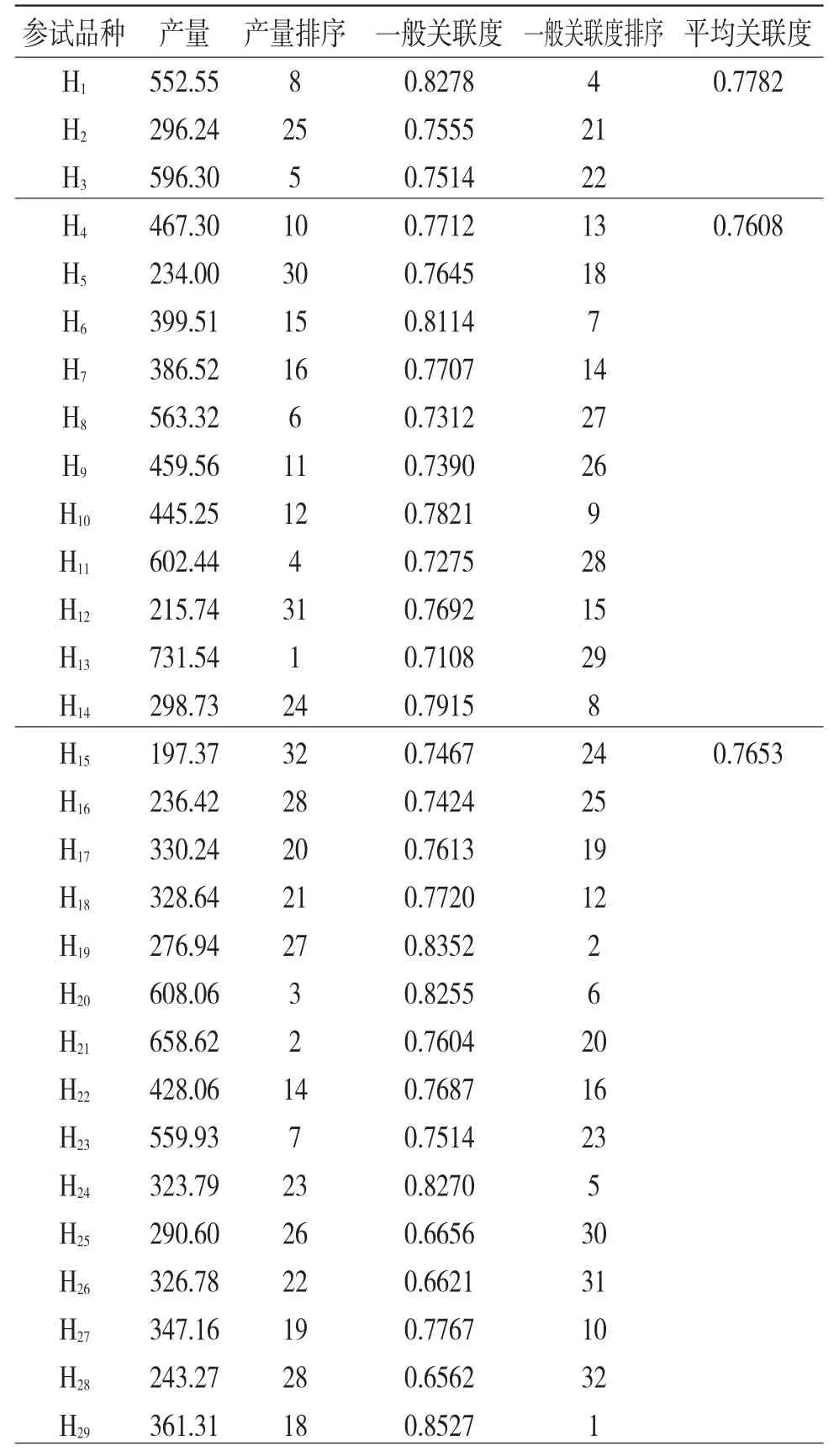
表5 不同品系的关联度及排序

H30 H31 H32 521.94 437.87 384.62 9 3 13 17 0.8279 0.7682 0.7758 17 11

3 结论与讨论

理想品种是我们认为最好的品种，关联度大的数列与理想品种数列最为接近[2]。通过以上分析可知，不同地区间的品种资源性状各有差异，各品种性状优缺点共存，产量性状好的关联度排名落后，而关联度排名靠前的产量又较低。其中日本品种H20（Y5）在一般关联度排序中居第6位产量位列3位，凉山品种H1（B130）关联度第8产量排第4，且综合各田间情况及穗部性状来看，其有效穗、穗实粒数、千粒重、结实率等主要经济性状优良，抗病性强，说明其能较好地适应当地环境种植，可以通过栽培技术的改进来提高产量，也可作为育种的亲本材料。

在本次试验中所试验的不同地区品种在地区品种平均关联度中，凉山品种最接近理想品种，云南的品种与理想品种差距较大，凉山品种与日本品种较接近。从表1中结实率和千粒重这两方面分析来看，可知云南品种的结实率较高，虽然H12（B126）在所有品种中产量排在第一，但是其它云南品种的有效穗比日本和凉山品种都低，最终影响它的地区品种平均关联度，但是可充分利用结实率高和千粒重大的优势用作育种材料。

注释及参考文献：

[1]灰色关联度分析法(好搜百科)[EB/OL]．http://baike．haosou．com/doc/6943274-7165637．html．

[2]戴红燕,殷显春,蔡光泽,等．灰色关联度分析在高原粳稻新品种评价上的应用[J]．西昌学院学报(自然科学版),2009,23(2):8-10．

[3]华劲松,戴红燕,苏解放,等．应用灰色关联度分析法对昭觉县高寒粳稻新品系分析评价[J]．西昌学院学报(自然科学版)，2014,28(1):8-12．

[4]朱鸿,官德义,杨军,等．福建花生种质资源筛选及灰色关联度分析[J]．福建农业学报,2008,23(4):381-386．

[5]戴红燕,蔡光泽,华劲松,等．凉山州地方粳稻品种性状研究[J]．西昌学院学报(自然科学版),2008,22(3):23-27．

[6]赖运平,李俊,张泽全,等．小麦苗期抗旱相关形态指标的灰色关联度分析[J]．麦类作物学报,2009,29(6):1055-1059．

[7]慕平,魏臻武,李发弟．用灰色关联系数法对苜蓿品种生产性能综合评价[J]．草业科学,2004,21(3):26-29．

[8]殷冬梅,李拴柱,崔党群．花生主要农艺性状的相关性及聚类分析[J]．中国油料作物学报,2010,32(2):212-216．

Analysis and Evaluation for Different Regions Agronomic Traits of Japonica Rice Germplasm Resources by Grey Correlation Degree Analysis Method

LUO Ya-lan，DAI Hong-yan，DING Xin，GUO Chang-chun，MA Rui，LI Ji-jin，MAO Ting-de，HUA Jin-song
(Xichang College,Xichang,Sichuan 615013)

In order to understand the difference character of Japonica Rice resources in different regions,and provide the parent materials for the breeding of new varieties,from Yunnan,Sichuan Liangshan Prefecture and Japan some Japonica Rice germplasm resources were compared in the same field.By means of grey correlation analysis, with determination and comparison of multiple trait data,the resource characteristics of each species were comprehensively evaluated.The results show that there were differences in the characteristics of the varieties among different regions,the coexistence of advantages and disadvantages of each variety traits,yield traits were well correlated after ranking,and the correlation degree of the top of the output was low,which Y5 and B130 can increase production through improvement of cultivation technology,but also can be used as parents in breeding materials.

Japonica rice germplasm;agronomic traits;grey relational analysis

S511.2+202.4

A

1673-1891（2015）04-0005-04

2015-08-31

四川省教育厅重点科研项目（15ZA0237）；西昌学院自立项目（15BZ01）：西昌学院大学生课外科研项目“不同地区粳稻种质资源农艺性状差异研究”。

罗雅兰（1993-），四川蒲江人，西昌学院2012级农学专业本科学生，研究方向：稻作资源。**为通讯作者。