同心分层注入水嘴尺寸确定方法
周理志韩国锋王发清刘曰武孟祥娟牛丛丛(.中国石油塔里木油田分公司,新疆库尔勒 84000;.中国科学院力学研究所,北京 0090)
引用格式:周理志,韩国锋,王发清,等.同心分层注入水嘴尺寸确定方法[J].石油钻采工艺,2015,37(5):95-99.
同心分层注入水嘴尺寸确定方法
周理志1韩国锋2王发清1刘曰武2孟祥娟1牛丛丛2
(1.中国石油塔里木油田分公司,新疆库尔勒 841000;2.中国科学院力学研究所,北京 100190)
引用格式:周理志,韩国锋,王发清,等.同心分层注入水嘴尺寸确定方法[J].石油钻采工艺,2015,37(5):95-99.
摘要:塔里木油田分层注水、注气井存在超深、高温、高压的特点,注入流体物性沿井深变化大,为了满足计算精度,必须充分考虑流体物性的变化。常见的注水水嘴计算方法无法达到精度要求,而注气水嘴的计算方法也未见报道。为此提出了满足塔里木油田分注要求的分层配注水嘴尺寸计算方法,由管柱中的流动得到嘴前压力、注入指数曲线得到注入压力,利用嘴前压力和注入压力,通过嘴流方程得到水嘴尺寸。在计算中需要考虑注水和注气在管流和嘴流方面的差别,充分考虑流体物性随温度和压力的变化,沿井深划分小段进行计算。此外,气体嘴流计算中的容积绝热指数需要通过热力学理论计算得到。在塔里木油田的工程实例中,该方法计算出的尺寸与实际尺寸接近,取得了较好的应用效果。
关键词:分层注水;水嘴;分层注气;注入指示曲线;嘴损曲线
塔里木四大主力砂岩油田轮南、东河、塔中、哈得逊等都采用注水开发,牙哈凝析气田采用注气开发,存在油藏层间储量动用程度差异大、注采井网不完善、平面上注采不平衡、注水井无法使各层受效、注水效率低等问题。塔里木油田从2001年开始分注工艺研究,在定向井、水平井和超深井的注水、注气工艺中取得了重大进展,目前亟需研发出满足油田分层注水、注气需求,可以分别计算不同层位注水量、注气量的水嘴尺寸确定方法。
常规分层注入工艺包括桥式偏心、同心集成、测调联动、同心管、恒流量配水等,其中同心集成、桥式偏心等工艺需要进行水嘴的投捞作业[1-2]。传统的“试凑法”成功率较低,需要反复投捞,施工周期长。塔里木油田分注井属于超深井,注入压力和地层温度高,注入流体物性沿井深变化大。相对于较高的注入压力,节流压力损失较小,为了得到满意的结果,节流压力损失的计算结果的相对精度要求比一般油气井高。为了提高计算精度必须充分考虑注入流体物性沿井深的变化,考虑储层注入能力数据的准确性。目前报道的计算方法在这方面考虑不够充分,另外分层注气的计算方法未见报道。以管流、嘴流、渗流理论为基础,根据塔里木油田的实际情况,结合其他油田注水水嘴的计算方法,充分考虑流体物性沿井深的变化及注入井的井身结构,提出了一套适合塔里木油田深层、高温、多井型的同心分层注水、注气配注水嘴尺寸的计算方法,并实现软件化[3-8]。
1 计算原理
水嘴尺寸可以利用流过水嘴的流量和嘴前、嘴后压力,通过嘴流方程确定,其中流量由各层位的配注量确定。对于注气,嘴流方程由水嘴尺寸、配注量、嘴前压力和嘴后压力确定。对于注水,嘴流方程由水嘴尺寸、配注量和水嘴压力损失确定,水嘴压力损失为
Δpch= pie– piw– Δpva(1)
式中,Δpch为水嘴压力损失,MPa;pie为嘴前压力,MPa;Δpiw为该层注入压力,MPa;Δpva为打开水嘴的启动压力,MPa,由配水器的类型确定。
因此,确定水嘴尺寸的关键在于计算嘴前压力和注入压力。嘴前压力由在一定的井口压力下通过流体在管柱中的流动方程确定。注入压力由配注量和地层注入能力确定。塔里木油田油井存在超深、高压、高温的特点,温度和压力沿井深会有较大变化,注入流体物性是压力和温度的函数,沿井深也会发生较大变化。为了计算准确,需要考虑不同井深处注入流体的物性,需要沿井深分成很多小段计算。因此,水嘴尺寸的计算包括管柱中的流动计算、嘴流计算、流体物性计算和地层流动计算。
2 分层注水水嘴尺寸确定方法
2.1 注水管流
对于注水,水的压缩性较小,其嘴前压力为
pie= piwh+ ph– Δpfr(2)
式中,piwh为井口压力,MPa;ph为液柱压力,MPa;Δpfr为沿程压力损失,MPa。
对于每一注水层的水柱压力,可以由该层以上的水柱重力决定
ph= ρgh = ρgLcosα (3)
式中,ρ为水的密度,kg/m³;g为重力加速度,m/s2;h为水柱的垂直高度,m;L为管柱长度,m;α为管柱倾角,°。式(3)考虑了井斜,能够适应不同井身结构的计算。
沿程摩擦压力损失由达西—魏斯巴赫公式确定[9]

式中,λ为沿程阻力系数,无量纲;d为注水管直径,m;L为油管长度,m;V为断面流速,m/s。
沿程阻力系数由雷诺数和注水管的当量粗糙度确定,根据雷诺数和当量粗糙度的不同,阻力系数有不同的计算公式。当雷诺数Re<2 300时,流动属于层流区,沿程阻力系数为

当处于紊流区时,科尔布鲁克拟合尼古拉兹水力光滑区和水力粗糙区公式,得到了适合紊流全区的经验公式为[9]式中,Δ为当量粗糙度,m。
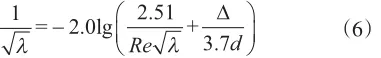
由于公式(6)需要迭代计算,比较麻烦,笔者使用Haaland公式进行拟合[9]

2.2 注水嘴流
水嘴压力损失和流量、水嘴尺寸之间存在函数关系,通过实验拟合和理论推导,水嘴压力损失、配注量及水嘴直径有关系式[10-13]
式中,Δpch为水嘴压力损失,MPa;C为实验确定常数,与其他参数使用的单位相关;n为实验确定常数,一般接近2.0;qiw为该层配注量,m3/d。式(8)中只要确定了压力损失和流量,就可求得水嘴的尺寸。
2.3 地层流动
注入水在地层中的流动情况决定了注入压力的大小,一般通过分层测试获得地层的流动属性。分层测试结果以分层注入指示曲线的形式表现,为了计算方便,编制软件时以数据表的形式存储。获得注入指示曲线后,分层注入压力piw可由相应层的配注量qiw从分层注入指示曲线求取。
分层测试结果一般以井口压力为视注入压力,为了得到相应层位的注入压力,需要校正到相应层位
piw= pie– Δpva–Δpch(9)
当没有进行分层流量测试且地层性质均匀,知道平均地层压力、表皮系数、注水半径等参数时,可计算地层吸水能力为
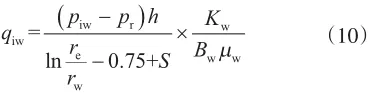
式中, qiw为相应层的配注量,MPa;pr为地层压力,MPa;re为注水半径,m;rw为井眼半径,m;S为表皮因数,无量纲;Kw为地层渗透率,mD;µw为水的黏度,mPa·s;Bw为水的体积系数,无量纲。
在其他文献中常见使用式(10)计算储层注入能力,但在塔里木油田注入井水嘴尺寸计算中,一般不使用这种方法,因为这种方法的精度较低,推荐使用实测的分层注入指示曲线确定注入压力。
2.4 注入水的物性计算
一般的注水计算中,把水的黏度和密度都当作常数。塔里木油田井深、高温、高压,注入压力高,温度和压力沿井深变化大,水的密度和黏度沿井深变化大,因此需要计算每一段水的高压物性。设计的计算软件使用了根据水的矿化度或者标准状态下密度计算水的高压物性的方法[14]。
3 分层注气水嘴尺寸确定方法
3.1 注气管流
注气时的嘴前压力计算需要利用气体在管道中的流动方程,气体在管道中的流动可以看作一维流动,通过质量守恒、动量方程和气体状态方程推导得到气体在管道中的流动方程为[15]
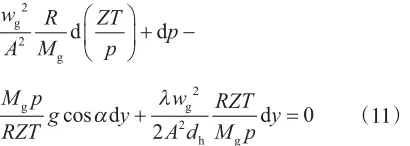
其中
Mg= ∑icimi(12)
dh= 4A/SA(13)式中,wg为质量流量,kg/s;A为油管横截面积,m2;R为普适气体常量,取值8.31 kJ/(kmol·k);Mg为平均分子量,kg/kmol;mi为第i组分的分子量,kg/kmol;ci为第i组分的分子数含量,%;dh为水力直径,m;SA为油管周长,m;Z为气体偏差因子,无量纲;T为温度,K;p为压力,MPa。
方程(11)中的沿程阻力系数与注水时情况相同。由于注水时水是从井口向井底流动,流动方向与生产时不同,因此上面方程符号与文献[14]有差别。方程(11)考虑了井斜的变化,加上分段考虑气体物性参数的变化,能够适应塔里木油田超深、高温、高压的特点和不同井型。
3.2 注气嘴流
气体在嘴孔中的流动包括临界流动和亚临界流动,当气体流速达到声速时为临界流动状态,低于声速时为亚临界流动状态。水嘴尺寸一定的情况下,流量随下游压力与上游压力之比减小而增大;小于临界压力之比以后,流量不变。相同上下游压力之比时,流量随水嘴尺寸的增大而增大。当气体的流动状态满足下面条件时,达到临界状态[16]

式中,k为气体绝热指数,无量纲。
气体在气嘴中的流动可以看作一个绝热等熵过程,可以推导出不同状态下的气体流量公式[16]。当气体流速达到临界状态时,气体的流量与下游压力无关
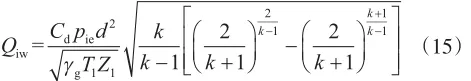
式中,Qiw为标准状态下的流量,104m3;Cd为与雷诺数和气嘴形状有关的系数,与其他参数使用单位相关;γg为气体相对密度,无量纲;Z1为上游气体偏差因子,无量纲;T1为上游气体温度,K。
当气体流量处于亚临界状态时,气体的流量为

通过上面的两个公式,在知道气体物性、温度、注入压力和嘴前压力的情况下,可以求得注气水嘴的尺寸。
3.3 注入气体的物性计算
计算注入气体在管柱中的流动需要使用气体的偏差因子和沿程阻力系数。而沿程阻力系数是由雷诺数和当量粗糙度决定的,因此需要使用气体的黏度。偏差因子和黏度随温度和压力变化。为了计算准确,沿井深的每一计算段都需要计算该段的气体平均黏度和偏差因子。气体高压物性的计算有很多方法,设计软件中提供了多种方法,如Standing、Lee等方法[14]。
气体在水嘴中的流动计算需要知道气体的绝热指数,一般采气工程教科书和文献资料上都把绝热指数当作常数。事实上,绝热指数也是温度和压力的函数,绝热指数分为容积绝热指数和温度绝热指数,嘴流计算中使用的实际上是容积绝热指数。对于理想气体,两个绝热指数相等;对于实际理想气体,两个绝热指数不等,容积绝热指数随温度和压力的变化较大。考虑到塔里木油田井深、高温、高压的特点,计算中不能把绝热指数当作常数,需要计算不同温度和压力下的容积绝热指数。根据热力学理论,可以得到气体容积绝热指数[17]

式中,kV为容积绝热指数,无量纲;cp为定压比热容,kJ/(kmol·k)。
计算容积绝热指数需要计算定压比热容、偏差因子及其对温度、压力的偏导数。偏差因子及其对温度和压力的偏导数可以通过实际气体的状态方程求得,常用的实际气体状态方程有PR、RKS、BWRS等。实际气体定压比热容可以通过单一组分理想气体定压比热容的经验关系、理想气体定压比热容与定容比热容的关系、实际气体定压比热容与理想气体定压比热容的关系、一般气体定压比热容与定容比热容的关系结合实际气体状态方程计算得到,具体公式见热力学相关书籍[17-18]。塔里木油田注气使用干气,属于混合气体,混合气体热力学计算需要使用混合规则,目前有很多混合规则,最简单的是Kay混合规则。在Kay混合规则中,混合气体的物性参数是其摩尔分数的加权平均。
4 计算软件
根据前述的水嘴尺寸确定方法,编制了分层注入计算软件,软件分为基础数据输入、测试数据输入、计算分析和水嘴调配,功能包括最小井口压力计算、水嘴尺寸计算、流体物性计算、沿程阻力系数的计算等,基础数据包括井型、注入流体及参数、水嘴参数、井身结构、分层参数和水嘴位置、温度数据,能够进行注水和注气计算,直井、斜井、水平井等井型的计算。软件界面如图1所示。软件界面分为上部菜单栏和工具栏,下部右侧图形窗口显示和下部左侧标签菜单。点击相应标签能够显示数据输入表和计算功能及结果表。软件能够在界面的右方同时显示不同层位的计算结果。通过设计井的基础参数和设计要求可以计算得到满足注入要求的最小井口压力。在给定井口压力不小于最小井口压力的情况下,可以计算得到不同层位达到注入要求所需的水嘴尺寸。通过不同井口压力条件下的计算结果,优选合适的结果作为设计方案。当输入参数精度低,计算结果与实测结果的差别不满足工程要求时,调配模块按照工程常用调配方法进行调配,减少投捞次数。
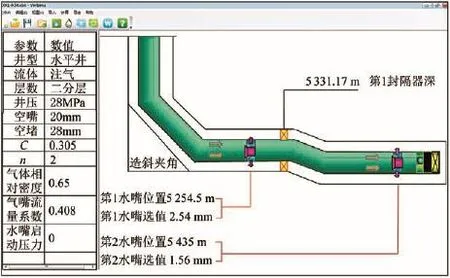
图1 计算软件界面
5 工程实例
利用塔里木油田分层测试数据进行验证。选取了5口井的分层测试资料,每口井都分为两个注入层段,通过分层测试获得了每口井的分层指示曲线和注入时的温度分布。由于没有对水嘴进行实验,所以将相同嘴型的其他多口井的实测数据进行拟合分析,所获得的参数作为目前5口井的嘴流计算参数。采用C取0.138,n取2.0,流体温度数据根据分层测试提供的温度输入,沿深度进行插值。利用获得的测试数据、井及管柱的基础数据、流体标准状况下的物性参数,计算分析了实际井口压力、注入量下的水嘴尺寸,并与实际使用的水嘴尺寸进行了对比,计算结果与实测结果对比见表1。从表1的结果可以看出,大部分情况下,计算的水嘴尺寸与实际尺寸很接近,XX10-2、XX10-4计算的水嘴尺寸偏差略大,但考虑到实际存在的各种误差,结果仍然是可以接受的。因此计算方法在实际应用中有较好的效果,能够满足塔里木油田的工程要求。
6 结论
(1)根据塔里木油田超深、高温高压井的特点,提出了分层注入水嘴尺寸的确定方法:由油管中的流动得到嘴前压力,由地层中的流动得到注入压力,最后通过嘴损曲线得到水嘴尺寸。
(2)分层注气水嘴尺寸的确定方法与分层注水水嘴尺寸的确定方法基本相同。由于气体压缩性较大,在管流方程和嘴流方程方面存在差别,注气和注水时需要使用不同的管流方程和嘴流方程。

表1 水嘴尺寸实际与计算结果对比
(3)注气嘴流方程中的容积绝热指数是温度和压力的函数,针对塔里木油田的注气情况,必须考虑容积绝热指数的变化。容积绝热指数可以通过实际气体状态方程,利用热力学理论计算得到。
(4)水嘴尺寸确定方法充分考虑了流体物性沿井深的变化,计算结果更加准确;考虑了井斜变化,能够适应不同井型的要求。编制了水嘴尺寸计算软件,工程实例计算表明,该软件适用于塔里木油田超深、高温、高压的环境和复杂的井型结构。
参考文献:
[1] 张玉荣,闫建文,杨海英,等.国内分层注水技术新进展及发展趋势[J].石油钻采工艺,2011,33(2):102-107.
[2] 刘合,裴晓含,罗凯,等.中国油气田开发分层注水工艺技术现状与发展趋势[J] .石油勘探与开发,2013,40(6):733-737.
[3] 王海勇,于晓杰.运用计算及编制程序选择注水水嘴[J].吐哈油气,2002,7(4):382-385.
[4] 石建设,陶晓玲,何建民.井下分层流量-压力测试与水嘴调配[J].石油机械,2003,31(1):39-41.
[5] 蒋国栋,李宏魁,王显章,等.非均质油藏分层配注水嘴优选方法研究[J].石油机械,2012,40(1):9-12.
[6] 邹艳华,李远,那贺忠.注水井分层流量调配方法研究[J].油气井测试,2003,12(3):4-6.
[7] 韩承骋,陈雷,孟康,等.桥式偏心分层注水水嘴选配方法研究[J].断块油气田,2013,20(5):659-662.
[8] 吕鹏.油田注水井分层注水中水嘴大小的研究与计算[J].湘潭师范学院学报:自然科学版,2008,30(1):57-58.
[9] 张鸣远. 流体力学[M].北京:高等教育出版社,2010.
[10] 蒋秀芳.用实验的方法求解配水器水嘴嘴损方程[J].江汉石油职工大学学报,2011,24(3):49-52.
[11] 韩洪升,付金辉,王春光,等.分层注水井配水嘴嘴损曲线规律实验研究[J].石油地质与工程,2008,22(2):79-81.
[12] 罗必林,巨亚锋,申晓莉,等.分层注水可调水嘴调节能力仿真计算与分析[J].石油天然气学报,2014,36(9):141-146.
[13] 申晓莉,于九政,王子建.新型小流量水嘴的设计与数值模拟[J].石油钻采工艺,2013,35(1):83-86.
[15] HAGOORT J.气藏工程原理[M].北京:石油工业出版社,1992.
[16] 李士伦.天然气工程[M].北京:石油工业出版社,2008.
[17] 朱明善,刘颖,林兆庄,等.工程热力学[M].北京:清华大学出版社,2011.
[18] 童景山.流体热物性学[M].北京:中国石化出版社,2008.
(修改稿收到日期 2015-07-14)
〔编辑 李春燕〕
Determining method of nozzle size used for concentric layered water injection
ZHOU Lizhi1, HAN Guofeng2, WANG Faqing1, LIU Yuewu2, MENG Xiangjuan1, NIU Congcong2
(1. Tarim Oilfield Company, CNPC, Korla 841000, China;
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China)
Abstract:The layered water and gas injection wells in Tarim Oilfield are characterized by super depth, high temperature and high pressure. The physical properties of injected fluids change greatly along the well depth. In order to ensure calculation accuracy, the changes of physical properties of the fluids must be fully considered. The common calculation methods for water injection nozzles are not adequate, and the calculation method for gas injection nozzle are not reported yet. This paper presents a set of methods for calculation of the sizes of layered water injection nozzles determined as per the requirement for separate layer injection in Tarim Oilfield, then the pre-nozzle pressure can be found by flow in the string and the injection pressure is found by the injection index curve. Then the nozzle sizes can be calculated by nozzle flow equation using the pre-nozzle pressure and injection pressure. The difference of pipe flow and nozzle flow of injected gas and water should be considered during calculation. The changes of physical properties of the fluids with temperature and pressure should also be fully considered. And the calculation should be carried out along the well depth in small sections. The isentropic volume change exponent during gas nozzle flow calculation can be found by thermodynamic theoretical calculation. In the engineering cases of Tarim Oilfield, the sizes calculated with this calculation method are close to the actual sizes, so this method acquires very good applied effect.
Key words:layered water injection; water nozzle; layered gas injection; injection indicator curve; nozzle loss curve
作者简介:周理志,1968年生。1990年毕业于西南石油大学采油工程专业,博士研究生,现主要从事采油、采气工程方面的研究工作,高级工程师。电话:0996-2172185。E-mail:zhoulz-tlm@petrochina.com.cn。
doi:10.13639/j.odpt.2015.05.024
文章编号:1000 – 7393(2015)05 – 0095 – 05
文献标识码:A
中图分类号:TE357
——2014版《陶瓷片密封水嘴》标准解读

