裂缝性碳酸盐岩酸化模拟新方法

罗 源杨乾龙刘平礼赵立强杜 勋徐 彬（.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都 60500；.中国石油长庆油田分公司第十采油厂，甘肃庆阳 74500）

引用格式：罗源，杨乾龙，刘平礼，等.裂缝性碳酸盐岩酸化模拟新方法［J］.石油钻采工艺，2015，37（5）：73-77.

裂缝性碳酸盐岩酸化模拟新方法

罗 源1杨乾龙2刘平礼1赵立强1杜 勋1徐 彬1
（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都 610500；2.中国石油长庆油田分公司第十采油厂，甘肃庆阳 745100）

引用格式：罗源，杨乾龙，刘平礼，等.裂缝性碳酸盐岩酸化模拟新方法［J］.石油钻采工艺，2015，37（5）：73-77.

摘要：在以往裂缝性碳酸盐岩酸化模拟的研究中，一般假设裂缝与基质均匀切割且将求解域离散为规则网格的形式，处理复杂形态的裂缝时会有较大困难。为了更加真实地模拟裂缝性碳酸盐岩的酸液流动过程，采用有限元网格对其求解域进行精细网格划分，使求解域更好地逼近各种复杂的裂缝形态，并且使用有限单元法进行模拟计算，实现对线性流和径向流酸化的模拟仿真，很好地解决了网格取向问题。结果表明，将有限单元法用以酸化模拟是可行的，为多孔介质内的精细酸化模拟提供了新方法。

关键词：裂缝；碳酸盐岩；酸化；有限单元法；模拟计算

对于裂缝性碳酸盐岩酸化，国内外做了大量研究。李勇明［1］、牟建业［2］等人在进行裂缝性碳酸盐岩酸化模拟时，将研究重点放在裂缝中蚓孔的增长和酸液对裂缝壁面的刻蚀。赵立强［3］、柳明［4］等人考虑了酸液在裂缝与地层孔隙介质之间的相互流动。但是大多数文献中所考虑的模型都较为理想化，多是将求解域离散为规则网格的形式，假设裂缝与基质均匀切割，采用有限差分法或有限体积法进行模拟计算。然而，当求解域中存在复杂形态的裂缝，裂缝和基岩之间几何形态和物性参数的巨大差异以及网格取向性问题，使规则网格形式逼近这类裂缝有较大困难。

有限元网格的形状可以是任意的，常应用于力学［5-7］和渗流问题［8-12］，在化学动力学问题上也有少量应用［13-15］，一定程度上说明了该方法在类似领域的可行性。牟行洋［16］通过有限单元法对含反应项的对流扩散方程进行了数值求解，其计算结果与解析结果吻合程度非常高，但其所求解的问题只有数学模型而没有结合具体实例。在前人研究的基础上，使用有限元网格对裂缝性碳酸盐岩区域进行精细网格划分，并使用相应的有限单元法对其中的酸液流动过程进行模拟，进行深入研究。

1　模型建立

1.1 模型假设条件

假设酸液在多孔介质中的渗流为单相流，裂缝和基岩中的流体渗流满足达西定律和质量守恒定律，忽略酸岩放热反应造成的温度变化对反应速度的影响。

1.2 数学模型

多孔介质中酸液浓度的分布受对流扩散作用以及反应过程的共同影响。酸溶蚀岩石后，岩石的孔隙度增大，渗透率和比面等参数也随之变化，这些参数之间的关系往往用经验公式进行表示。Kalia［17］用双重尺度模型来表示这一系列关系。

1.2.1 达西尺度模型 压力场模型即渗流微分方程，其表达式为

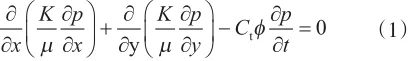
式中，K为渗透率，mD；µ为酸液黏度，mPa·s；p为压力，MPa；Ct为流体和岩石的总压缩系数，MPa-1；为孔隙度，%；t为时间，s。

根据物质平衡原理，某一微元内浓度的变化等于对流扩散产生的浓度变化加上反应过程产生的浓度变化，其表达式为

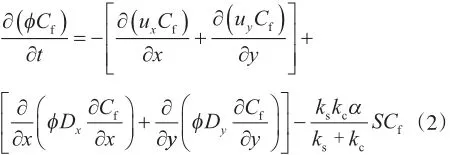
其中

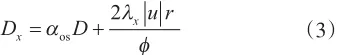
式中，Cf为酸液浓度，mol/L；u、ux、uy分别为流体流速、x方向的流速、y方向的流速，m/s；D、Dx、Dy分别为扩散系数、x方向的扩散系数、y方向的扩散系数，m2/s；ks为表面反应速率常数，m/s；kc为传质系数，m/s；α为酸的溶解能力，g/mol；S为比面，m-1；αos、λx和λy为与岩石结构有关的常数；r为孔隙半径， µm。

流速u由所得到的压力场依据达西定律计算

式中，∇p为压力梯度，MPa/m。

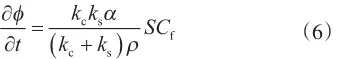
孔隙度变化为

式中，ρ为岩石密度，kg/m3。

1.2.1 孔隙尺度模型 Kalia的孔隙尺度模型反映了渗透率、比面以及孔隙半径等物性参数随孔隙度的变化。渗透率响应为

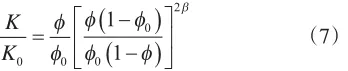
式中，K0为初始渗透率，mD；0为初始孔隙度，%；β为渗透率与孔隙度关系指数，通过实验获得。

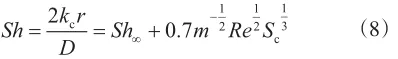
其中

式中，Sh为舍伍德数；Sh∞为渐进舍伍德数；m为孔隙长度与直径比；Re为雷诺数；um为边界流体流速， m/s；r0为初始孔隙半径， µm；ν为运动黏度，cm2/s；Sc为施密特数。

孔隙半径与渗透率和孔隙度之间的关系式为

比面与孔隙度和孔隙半径之间的关系式为式中，S0为初始比面，m-1。

1.3 定解条件

第一类边界条件：流出端为恒定压力边界，流入端为恒定浓度边界（t＞0）。

系统电源电路主要作用是为PS12034功率模块提供 +15 V电源，为延时电路提供+24 V电源，为控制电路提供+5 V电源。选用输入交流AC380 V/50 Hz输出带有+24 V、+15 V和+5 V的开关电源。

第二类边界条件：流入端为恒定流速边界。

初始条件：初始时刻整个区域中的压力为一定值，压力浓度为0。

由于对径向流的模拟采用的仍是以上数学模型，所以这里没有周期边界条件。对于封闭边界，边界流速为0，模型在用有限单元法离散的积分形式中的线积分项也为0，所以也省略了封闭边界条件。

2　模型求解

2.1 裂缝性碳酸盐岩物理模型

2.1.1 线性流模型的网格划分 以酸液在碳酸盐岩中的二维流动为例，假设裂缝形状为交叉裂缝和弧形裂缝，岩心大小为5 cm×2.5 cm，酸液从左端流入，从右端流出，类似于碳酸盐岩岩心的酸液流动实验。通过设置超大孔隙度区域（孔隙度为0.9）来模拟裂缝，设置小孔隙度区域（平均孔隙度为0.12，变化范围为0.02~0.22）来模拟致密区域。

计算区域的网格划分如图1所示，在裂缝附近进行了加密处理。采用三角形单元划分整个求解域，有限元网格可以很好地逼近这类存在复杂裂缝的情况。虽然一般情况下，四边形单元与三角形单元相比有更好的计算精度，但三角形单元能更好地适应各种复杂边界以及其他形状较为曲折或有尖角的曲面，为了使网格较好地逼近各种复杂形态的裂缝，文中均使用三角形单元来进行网格划分。为清楚地看到裂缝附近的网格划分情况，将图1中红色矩形圈出部分放大，得到局部放大图如图2所示。

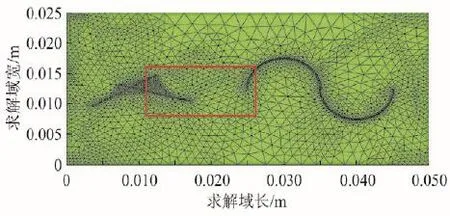
图1　 裂缝性碳酸盐岩网格划分

图2　 裂缝性碳酸盐岩网格划分局部放大

2.1.2 径向流模型的网格划分 酸液由井筒向地层的流动为径向流，由于有限元网格的灵活性，这里研究酸液流动时与Kalia、柳明等人不同，并没有建立极坐标系下的酸液流动反应模型，坐标系仍然采用的是直角坐标系，径向流条件下的网格形式与线性流也没有区别，井眼半径和伤害带半径分别设为0.12 m和1 m，如图3所示。

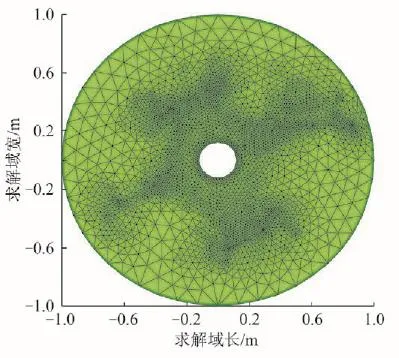
图3　 近井多条裂缝网格划分

2.2 数学模型离散

2.2.1 压力场模型离散 对求解域中的任意一个单元e，首先对式（1）使用加权余量法为

其中

ωl=Nl（14）

p=Nipi+Njpj+Nmpm（15）

l=i,j,m （16）

式中，ωl为权函数；p为该单元内的压力近似插值函数；pi、pj、pm分别为单元节点的假设压力值，MPa；Ni、Nj、Nm为基函数。

将式（13）写成其对应的等效积分弱形式，并代入式（14）、（15）、（16），得到该单元内的半离散格式为式中，Ke、Me和Fe分别为计算得到的单元刚度矩阵、单元温度矩阵和单元载荷向量；Pe为未知的单元压力向量。

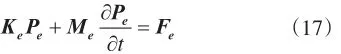
按时间向后差分格式计算为

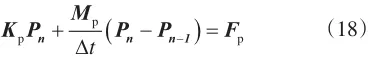
式中，∆t为时间步长，s；Kp、Mp和Fp分别为计算得到的总体刚度矩阵、总体温度矩阵和总体载荷向量；Pn-1和Pn分别为上个时步和该时步的压力场向量，MPa。该时步内Pn-1为已知。

2.2.2 浓度场模型离散 对于浓度分布模型式（2），其中的速度u则通过所得的压力场由式（5）计算，类似压力场模型的离散过程，同样可以得到

式中，Kc、Mc和Fc分别为计算浓度场的总体刚度矩阵、总体温度矩阵和总体载荷向量；Cn-1和Cn分别为上个时步和该时步的浓度场向量。

得到求解域中的浓度分布后，则可按式（6）~（12）计算孔隙度和渗透率等物性参数，并将其代入下个时步继续计算。

3　计算实例

根据上述模型和方法，使用Matlab编制模拟计算程序，利用表1中的数据进行模拟计算。

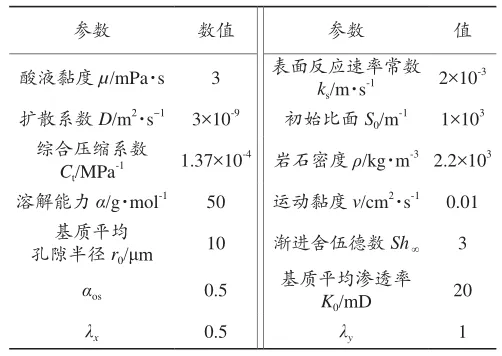
表1　模型参数

3.1 线性流模拟

在相同注酸量的前提下，图1模型分别以1×10-6m/s、1×10-5m/s和1×10-4m/s的注酸速率进行注酸，溶解形态如图4所示。注酸速率较低时（1×10-6m/s），端面溶蚀程度较大，酸液作用距离有限；注酸速率较高时（1×10-4m/s），虽然更多区域被溶蚀，但是无法得到足够大的渗透率；在注酸速率适中时（1×10-5m/s），形成具有相当导流能力的溶蚀通道。

为了评价酸化效果，优选工艺参数，将岩心（或伤害带）突破的标志定义为入口压力降为初始值的1%，将无因次突破体积定义为岩心突破时的酸液注入体积与岩心（或伤害带）孔隙体积之比。如图5所示，随着注酸速率的增加，突破体积呈现先减小后增加的趋势，即注酸速率存在一个最优值，这里为1×10-5m/s。

3.2 径向流模拟

图3模型分别以1×10-5 m/s、5×10-4 m/s和5×10-3 m/s的注酸速率注酸，不同溶解形态如图6所示，可以看出，溶解形态同样形成了面溶蚀、蚓孔和均一溶蚀。低注酸速率（1×10-5m/s）下靠近井筒的裂缝缝宽增大，端面溶蚀程度大，但酸液作用距离有限；高注酸速率（5×10-3m/s）下形成了多分支孔道，连通多条裂缝，但不能得到足够大的渗透率；注酸速率（5×10-4m/s）适中时形成一条高渗通道。如图7所示，得到最优注酸速率为5×10-4 m/s。

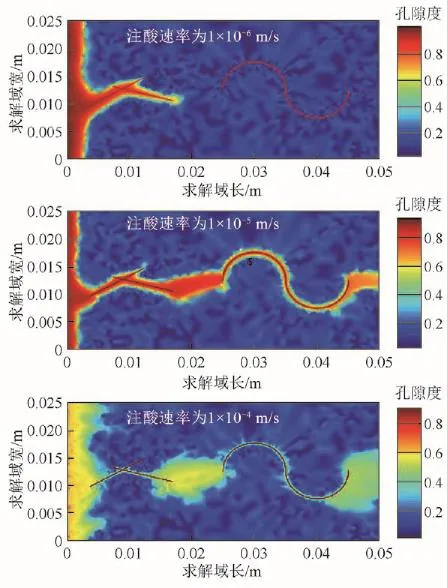
图4　 线性流在不同注酸速率下的溶解形态

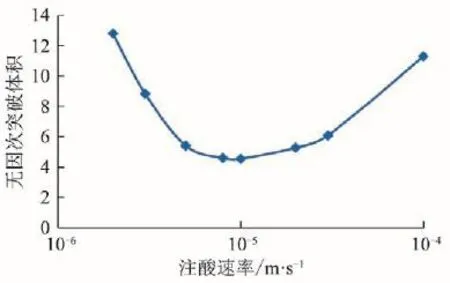
图5　 线性流无因次突破体积与注酸速率曲线

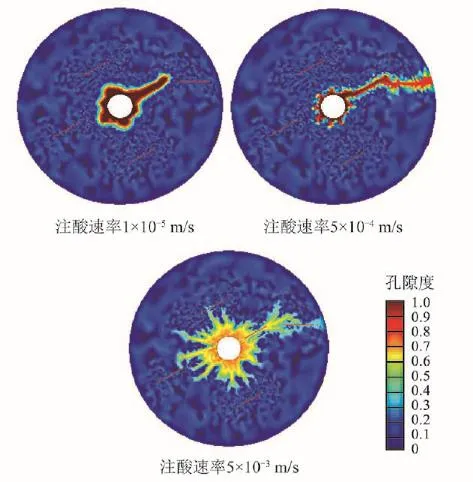
图6　 径向流在不同注酸速率下的溶解形态

图7　 径向流无因次突破体积与注酸速率曲线

4　结论和建议

（1）利用有限单元法建立了与双重尺度模型相对应的数值模型，研究了裂缝性碳酸盐岩储层酸化特点。裂缝性碳酸盐岩储层酸化存在最优注酸速率，该速率下酸液突破岩心或伤害带所需用酸量最少。虽然原始储层中存在的微裂缝几乎不能为地下流体的渗流作贡献，酸化作业可能会使这些裂缝彼此连通从而形成高渗孔道。

（2）有限元网格能较好地逼近各种复杂形态的裂缝，可同时实现对线性流和径向流酸化的模拟，解决了网格取向问题。

（3）暂时没有考虑矿物成分分布的影响，且所研究的仍是二维模型，下一步需要开展考虑了矿物成分的三维模型研究，做到真正意义上的仿真模拟。

参考文献：

［1］ 李勇明，郭建春，赵金洲，等.裂缝性油藏酸液滤失模型研究［J］.西南石油学院学报，2004， 26（2）：50-53.

［2］ 牟建业，张士诚.酸压裂缝导流能力影响因素分析［J］.油气地质与采收率，2011，18（2）：69-71，79.

［3］ 赵立强，刘平礼，刘向东，等.裂缝性碳酸盐岩基质酸化设计计算方法研究［J］.天然气工业，2001，21（4）：69-71.

［4］ 柳明，张士诚，牟建业，等.碳酸盐岩油藏非均质性对蚓孔扩展的影响［J］.特种油气藏，2012，19（5）：146-150.

［5］ 王志坚，邓卫东，林忠超，等.水平井封隔器卡瓦的有限元分析及结构改进［J］.石油钻采工艺，2013，35（4）：78-81.

［6］ 陈占锋，朱卫平，狄勤丰，等.偏磨套管破裂强度三维弹塑性有限元分析［J］.石油钻采工艺，2013，35（6）：1-4.

［7］ 张辉，高德利，段明星，等.欠平衡钻井条件下地层造斜特性研究［J］.石油钻采工艺，2012，34（2）：1-3.

［8］ 赵敏.油藏中人工裂缝渗流规律的有限元法分析［D］.中国科学院研究生院：渗流流体力学研究所，2006.

［10］ 李亚军，姚军，黄朝琴，等.考虑渗透率张量的非均质油藏有限元数值模拟方法［J］.计算物理，2010，27（5）：692-698.

［11］ 姚军，张娜，黄朝琴，等.非均质油藏多尺度混合有限元数值模拟方法［J］.石油学报，2012，33（3）：442-447.

［12］ 许广明，孔祥言，卢德唐.利用非稳定渗流方程研究射孔参数对产能的影响［J］.石油钻采工艺，2000，22（4）：42-45.

［13］ KASHID M N, AGAR D W, TUREK S. CFD modelling of mass transfer with and without chemical reaction in the liquid–liquid slug flow microreactor［J］. Chemical Engineering Science, 2007, 62（18）： 5102-5109.

［14］ SEDDEEK M A. Finite-element method for the effects of chemical reaction, variable viscosity, thermophoresis and heat generation/absorption on a boundary-layer hydromagnetic flow with heat and mass transfer over a heat surface［J］. Acta Mechanica, 2005, 177（1）: 1-18.

［15］ ZHAO C, HOBBS B E, MÜHLHAUS H B, et al. Finite element modelling of dissipative structures for nonequilibrium chemical reactions in fluid-saturated porous media［J］. Computer Methods in Applied Mechanics and Engineering, 2000, 184（1）: 1-14.

［16］ 牟行洋.二维对流扩散方程的有限元求解及其反问题研究［D］.西安：西安理工大学，2009.

［17］ KALIA N, BALAKOTAIAH V. Modeling and analysis of wormhole formation in reactive dissolution of carbonate rocks［J］. Chemical Engineering Science, 2007, 62（4）: 919-928.

（修改稿收到日期 2015-08-02）

〔编辑 李春燕〕

A new simulation method for fractured carbonate acidizing

LUO Yuan1, YANG Qianlong2, LIU Pingli1, ZHAO Liqiang1, DU Xun1, XU Bin1
（1. State Key Laboratory of Oil & Gas Reservoir Geology and Exploitation , Southwest Petroleum University, Chengdu 610500, China;
2. No.10 Oil Production Plant of Changqing Oilfield Company, CNPC, Qingyang 745100, China）

Abstract:In the previous research on simulation of fractured carbonate acidizing, it is generally assumed that the fractures cut the matrix uniformly and that the solution domain is dispersed into regular mesh pattern, which may find it very difficult to process fractures with complex shapes. In order to simulate the acid flow response process of fractured carbonate more realistically, this paper uses finite element mesh to carry out fine mesh division to its solution domain, so that the solution domain can better approach the various complex fracture shapes. In addition, finite element method is used to perform simulation, which realizes analog simulation of linear flow and radial flow acidization, favorably addressing the problem of mesh orientation. The results show that it is workable that finite element method is used for acid simulation, providing a new technique for fine acid simulation inside porous media.

Key words:fracture; carbonate; acidification; finite element method; simulation

作者简介：罗源，1987年生。西南石油大学油气田开发工程专业在读硕士研究生，现主要从事油气藏储层改造方面的研究工作。电话：15928639637。E-mail：lyluoyuan@126.com。

基金项目：国家自然科学基金“复杂非均质碳酸盐岩储层水平井酸化高效布酸基础理论研究”（编号：51474182）。

doi:10.13639/j.odpt.2015.05.018

文章编号：1000 – 7393（2015）05 – 0073 – 05

文献标识码：A

中图分类号：TE357