溶解气驱油藏非完善井流入动态方程
任宗孝吴晓东赵金赢安永生李 准邢 强(.中国石油大学石油工程教育部重点实验室,北京 049;.中国石油华北油田分公司第四采油厂,河北廊坊 065000;.延长油田股份有限公司勘探开发技术研究中心,陕西延安 76000)
引用格式:任宗孝,吴晓东,赵金赢,等.溶解气驱油藏非完善井流入动态方程[J].石油钻采工艺,2015,37(5):68-72.
溶解气驱油藏非完善井流入动态方程
任宗孝1吴晓东1赵金赢2安永生1李 准1邢 强3
(1.中国石油大学石油工程教育部重点实验室,北京 102249;2.中国石油华北油田分公司第四采油厂,河北廊坊 065000;3.延长油田股份有限公司勘探开发技术研究中心,陕西延安 716000)
引用格式:任宗孝,吴晓东,赵金赢,等.溶解气驱油藏非完善井流入动态方程[J].石油钻采工艺,2015,37(5):68-72.
摘要:Standing在Vogel方程的基础上建立了溶解气驱油藏非完善井的IPR方程,但这一方程并未得到国内外学者的一致认可。通过分析Standing产能方程,指出Standing定义的流动效率(油井在同一产量下理想井底压差与实际井底压差之比)是建立在油藏单相渗流理论基础之上,并不适用于油气两相渗流。选用相同压降下实际油井产量与理想油井产量之比定义流动效率,建立了新的非完善井产能预测方程,该方程计算结果的正确性得到了油藏数值模拟结果的验证。
关键词:溶解气驱油藏;非完善井;产能方程;Standing方程;IPR曲线;流动效率
1968年Vogel[1]应用Weller[2]方法通过计算机模拟出了21种典型溶解气驱油藏的无因次IPR曲线,并建立了预测溶解气驱油藏流入动态的Vogel方程。该方程由于运算简便、计算精度高、适用范围广,获得了广大油藏工程师的认可。但Vogel方程没有考虑油藏在钻完井过程中受到的伤害对油井产能的影响。1972年Standing[3]为了预测非完善井的产能,利用流动效率的定义式考虑了油井表皮因数对产能的影响,进而在Vogel方程的基础上建立了非完善油井产能预测方程。该方程扩大了Vogel方程的应用范围,为评估油井在进行增产措施后产能的变化提供了理论依据。Standing方程也迅速引起了国内外油藏工程师的兴趣,相继在Standing方程的基础上做了大量研究工作。国内以陈元千教授为代表,基于文献[1]、 [3]、 [4]提出了既考虑油井不完善程度又考虑不同采出程度影响的无因次IPR方程[5],并在文献[6]中提供了利用不关井两点测试法计算油井流动效率的方法。国外学者Harrision[7]在Standing方程的基础上进一步扩大了该方程的应用范围,但该文献并未公开发表。此外Lekia和Evans[8]在Standing方程的基础上,同样做了扩大该方程的应用工作。Nind[9]在1986年提供了利用两点试井法计算Standing流动效率的方法。
然而Standing建立溶解气驱非完善井产能预测方程后,方程计算结果的正确性也受到了学者的广泛质疑。1983年Whitson[10]指出当流动效率较高时Standing方程计算结果有误。1984年Brown[7]提出当流动效率较高或流压较低时Standing方程计算结果会出现问题。1989年Camacho-V[11]指出Standing方程假设单相渗流中流动效率的定义式同样适用于油气两相渗流是不正确的,并提出了一个新的二项式流动效率计算公式。
Standing为了把Vogel方程的应用范围扩大到非完善井,本质上做的工作就是引入了考虑非完善井表皮因数影响的油井流动效率,认同Standing方程的学者在此基础上做了更进一步的研究。还有一部分学者认为Standing方程中的流动效率定义式有误,他们有的指出了出现错误问题的情况,有的重新建立了油井流动效率定义式。因此,有关Standing方程正确性的问题仍需进一步的探讨。
1 Standing产能方程
Standing在文献[3]中同时给出了2个具有不同物理意义的流动效率定义式。第1个流动效率的定义式为
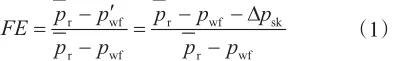
式中,FE为流动效率,实数;pr为地层压力,MPa;p′wf为理想井底流压,MPa;pwf为实际井底流压,MPa;Δpsk为近井地带污染产生的附加压降,MPa。
Standing认为考虑近井地带污染后的实际油井渗流压降与理想油井渗流压降关系如图1所示。可以看出,在流体达到污染半径rs之前,同一产量下实际油井油藏渗流压降曲线和理想油井油藏渗流压降曲线是完全一致的。当油藏流体到达污染半径rs后,实际油井受近井地带污染影响,流体的渗流阻力增大,压降曲线斜率增加,到达井筒时井底流压为pwf;由于理想油井附近无污染表皮因数的影响,压降曲线斜率保持不变,到达井筒时的井底流压为p′wf。通过上述分析可知,式(1)的本质为油井在同一产量下理想井底压差与实际井底压差之比。
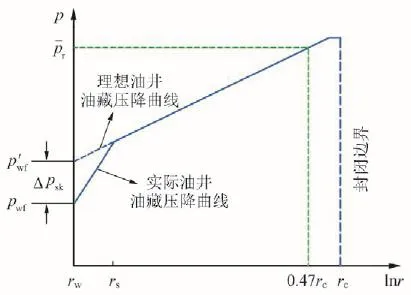
图1 油藏渗流压降简图
依据式(1)的定义,Standing在Vogel方程的基础上建立了溶解气驱油藏非完善井的产能预测方程式中,qo为实际油井产量,m3/d;qomax(FE=1)为理想油井最大产量,m3/d。
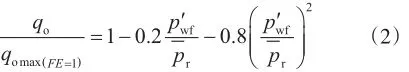
2 新的非完善井流入动态方程
在文献[3]中Standing同时提出了第2个考虑油井污染影响的流动效率定义式,其表达式为式中,Ef为流动效率,实数;re为泄油半径,m;rw为井眼半径,m;S为表皮因数,实数。

式(3)的物理意义为相同压降下实际油井产量与理想油井产量之比,对比2个流动效率的定义,可知Standing同时给出了2个物理意义不同的流动效率定义式。
依据式(3)的物理意义可得

式中,qo′为理想油井产量,m3/d。
由Vogel方程可知溶解气驱油藏完善井的产能预测方程为

由式(4)和式(5)联立可得相同井底流压下实际油井的产能预测方程为

式(6)是从式(3)的物理意义出发,重新建立的溶解气驱油藏非完善井流入动态方程(下文称式(6)为新非完善井产能预测方程)。
3 两种产能预测模型的对比
Standing在建立非完善井产能预测方程时,同时给出了2种不同概念的油井流动效率定义式。下面通过实例分析Standing产能预测方程式(2)和新的非完善井流入动态方程式(6)的区别。
假设圆形封闭油藏中心一口井,在拟稳态条件下生产。地层压力25 MPa,泡点压力30 MPa,油藏半径为300 m,井眼半径为0.16 m。已知油井现在为完善井,当井底流压为10 MPa时油井产量为30 m3/d。用式(2)和式(6)分别计算当流动效率为0.5、0.7、1、1.2、1.5、2时该井的IPR曲线,见图2、图3。
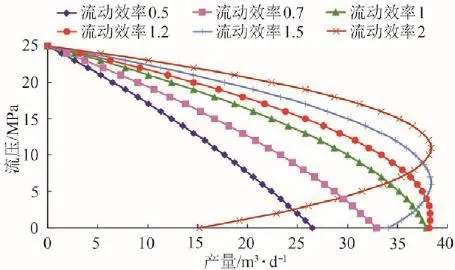
图2 Standing方程流入动态曲线
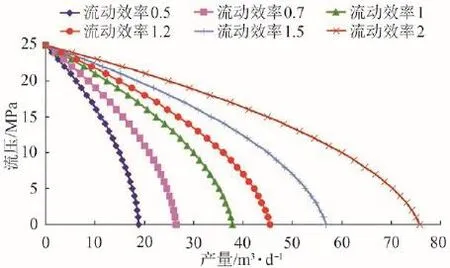
图3 新非完善井产能预测方程流入动态曲线
从图2、3可以清晰地看出,在油藏参数、生产数据完全相同的情况下,由两种产能预测方程计算得出的油井产能曲线有明显的区别。Standing方程的计算结果出现了以下不合理的情况:①在高流动效率及低井底流压的情况下,出现了井底流压越低油井产量越低的现象;②相同生产压差下,高流动效率的油井产量反而比低流动效率的油井产量低。而图3显示油井的产量随井底生产压差的增大而增加,且在相同井底流压下流动效率高的油井比流动效率低的油井产量大,计算结果没有出现明显的不合理情况。
4 Standing产能方程正确性判断
4.1 Standing方程中流动效率定义式的建立
Standing在引用第1个流动效率定义式建立产能预测方程时,并没有给出该定义式的建立过程,下面详细介绍式(1)的建立过程。
1953年Everdingen[13]、1956年Hurst[14]分别提出用表皮因数来考虑油井近井地带污染对井底压力的影响。Everdingen在均质地层单相流微可压缩不稳定渗流模型的基础上,建立了考虑油井表皮因数影响的非完善井单相流体不稳定渗流时井底压力计算公式
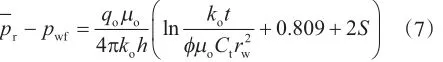
式中,μo为地层油的黏度,Pa·s;ko为原油渗透率,m2;h为油藏有效厚度,m;为地层孔隙度,小数;Ct为地层综合压缩系数,MPa-1。
Brownscombe[ 15]指出在单相渗流情况下,可用单相稳定渗流公式代替单相不稳定渗流公式,计算由油井表皮因数引起的额外压降,其表达式为
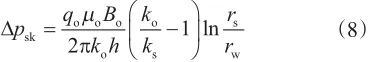
式中,rs为污染半径,m;ks为污染带渗透率,mD。
1956年Hawkins[16]在Everdingen井底压力公式(即式(7))的基础上,给出了油井表皮因数的计算公式
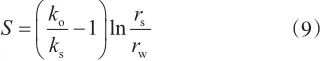
将式(9)代入式(8)可得由于油井污染引起的额外压降计算公式
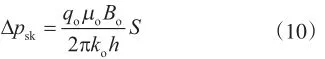
Standing正是在此压降的基础上,提出了理想井底流压的概念,考虑了油井表皮因数的影响,建立了式(1)。通过以上陈述可知,Standing定义的第1个流动效率定义式是建立在油藏单相渗流理论基础上的。Nind[9]证实了在单相渗流情况下,该定义式是正确的。本文从另一个角度,佐证第1个流动效率定义式在油藏单相渗流中的正确性。油藏单相渗流产能计算公式为[17]

式中,J为产液指数(在油藏单相渗流情况下为定值),m3/MPa。
将式(11)代入式(10)得
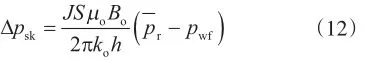
式(12)代入式(1)并化简得
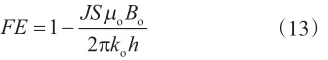
式(13)中等式右边参数对于特定的单相流油藏而言都是常数,所以方程右边为常数,左边也为常数,则式(13)在理论上是成立的。但在油气两相渗流中式(1)是否成立需要做进一步的证明。
4.2 Standing产能方程的错误
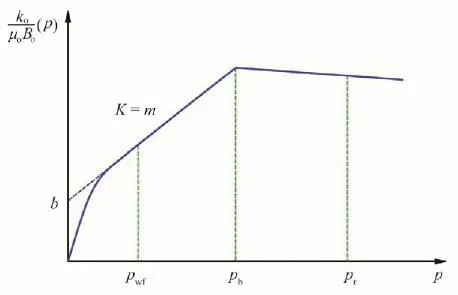
图4 ko ( p)与压力的关系µo Bo
Fetkovich指出当井底流压为0<pwf<pb(泡点压力)时, 与油层压力的关系可以假设为通过原点的线性关系,表达式为
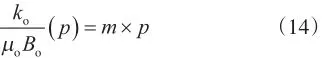
式中,m为直线的斜率,实数;p为不同位置油藏的压力,MPa。
井底流压为pwf时的平均值(为 p)

化简式(15)得

将式(16)代入式(10)化简得

将式(17)、式(5)代入式(1)并化简得

式(18)中右边S、h、m、qomax、 pr对于特定的油藏来说都是常数,唯一变化的量是井底流压pwf,那么方程右边是随井底流压变化的变量,而左边为常数。所以在溶解气驱两相流动中,流动效率的定义式(1)是不成立的,则以此为基础而建立的Standing产能方程也是不成立的。
由以上内容可知,Standing提出的流动效率定义式(1)是建立在油藏单相渗流理论基础上的。在其发表的论文中直接给出了流动效率定义式(1),并依此建立了溶解气驱油藏两相渗流的非完善井产能预测方程。作者基于两相渗流理论中的Vogel产能方程以及Fetkovich提出的原油物性随油藏压力变化的公式,证明了流动效率定义式(1)在油气两相渗流情况下不满足等式关系,并找到了Standing产能方程计算错误的原因。
5 新非完善井产能方程的正确性
1992年Klins[19]在Weller方法的基础上应用Hawkins[16]表皮因数定义式即式(9),对井底受污染的圆形封闭溶解气驱油井产能进行了数值模拟,并对模拟结果进行了非线性回归分析,得到溶解气驱油藏非完善井的产能预测方程

式(19)中的参数M,Klins称之为油井非完善性影响系数,其表达式为
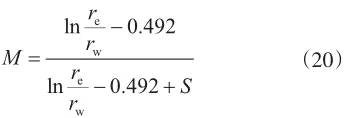
式(19)形式与前面建立的溶解气驱油藏新非完善井产能预测模型完全一致,并且非完善性影响系数M的计算公式与前文的公式(3)唯有一常数值有微小差别。Klins基于油藏数值模拟结果通过非线性回归分析得到的溶解气驱油藏非完善井产能预测方程与本文通过理论研究建立的非完善井产能预测方程几乎一致,证实了本文所建新非完善井产能预测方程的正确性。
6 结论
(1)Standing产能方程中流动效率定义式(即式(1))是在油藏单相渗流的基础上建立的,在溶解气驱两相渗流情况下该流动效率的定义式是不成立的,导致了Standing产能方程计算结果的不合理。
(2)Standing在其文献中给出了2个不同的油井流动效率定义式,且物理意义各不相同。在油气两相渗流情况下油井流动效率的概念应为相同生产压差下实际油井产量与理想油井产量之比,而非相同产量下理想生产压差与实际生产压差之比。
(3)本文依据第2个流动效率定义式,建立了新的溶解气驱油藏非完善井产能预测方程,该方程考虑了近井地带污染对油井产能的影响,扩大了Vogel方程的使用范围,而且其正确性也得到了Klins数值模拟结果的佐证。
参考文献:
[1] VOGEL J V. Inflow performance relation-ship for solution-gas drive wells[J]. Journal of Petroleum Technology,1968,20(1): 83-92.
[2] WELLER W T. Reservoir performance during two-phase flow[J]. Journal of Petroleum Technology,1966,18(2): 240-46.
[3] STANDING M B. Inflow performance relationship for damaged wells producing by solution-gas drive [J]. Journal of Petroleum Technology,1970,22(11): 1399-1400.
[4] RICHARDSON J M, SHAW A H. Two rate IPR testing a practical tool[J]. Petroleum Society of CIM, 1982, 3(5): 81-82.
[5] 陈元千.无因次IPR曲线通式的推导及线性求解方法[J].石油学报,1986,7(2):63-72.
[6] 陈元千.确定油井流动效率的两点法[J].油气井测试,1990(4): 7-11.
[7] BROWN K E. The echnology of artifical lift methods [M]. Vol. 2. PPC Books,1984.
[8] LEKIA S D L,EVANS R D. Generalized inflow performance relationship for stimulated wells [J]. Journal of Canadian Petroleum Technology, 1990, 29(6): 32-37.
[9] NIND T E W. Skin factor and flow efficiency in wells producing under solotion gas drive[J]. Journal of Canadian Petroleum Technology, 1986, 25(4): 31-34.
[10] WHITSON C S. Reservior well performance and predicting deliverability [R]. SPE 12518, 1983.
[11] CAMACHO-V R G, Raghavan R. Inflow performance relationships for solution-gas-drive reservoirs [R]. SPE 16204, 1987.
[12] WIGGINS M L. Generalized inflow performance relationship for three-phase flow[R]. SPE 25458, 1994.
[13] Van EVERDINGEN A F. The skin effect and its influence on the productive capacity of a well [J]. Journal of Petroleum Technology, 1953, 5(6): 171-176.
[14] HURST W. Estabilishment of the skin effect [J]. AIME, 1956, 8(20), 356-357.
[15] BROWNSCOMBE E R, COLLINS F. Pressure distribution in unsaturated oil reservoirs [J]. Journal of Petroleum Technology, 1950, 2(10): 9-10.
[16] HAWKINS Jr M F. A note on the skin effect[J]. Journal of Petroleum Technology, 1956, 8(12): 65-66.
[17] 张琪.采油工程原理与设计[M].山东东营:中国石油大学出版社,2000:4-5.
[18] FETKOVICH M J. The isochronal testing of oil wells [R]. SPE 4529, 1973.
[19] KLINS M A, MAJCHER M W. Inflow performance relationship for damaged or improved wells producing under solution gas drive [J]. Journal of Petroleum Technology, 1992, 44(12): 1357-1363.
(修改稿收到日期 2015-08-22)
〔编辑 朱 伟〕
Inflow performance equation of partially penetrated well in solution gas drive reservoirs
REN Zongxiao1, WU Xiaodong1, ZHAO Jinying2, AN Yongsheng1, LI Zhun1, XING Qiang3
(1. Key Laboratory of Education Ministry for Petroleum Engineering, China University of Petroleum, Beijing 102249, China;
2. No. 4 Oil Production Plant of Huabei Oilfield Company, CNPC, Langfang 065000, China;
3. Research Center of Exploration and Development Technology, Yanchang Oil field Co.Ltd, Yan’an 716000, China)
Abstract:Standing established the IPR curve equation for partially penetrated wells in solution gas drive reservoirs based on Vogel equation. But Standing’s equation is not unanimously accepted by scholars from both home and abroad. The analysis of Standing’s equation on productivity shows that the flow efficiency defined by Standing (the ratio of ideal hole bottom pressure differential with and actual bottom pressure differential under the same production of the oil well) is based on theory of single phase flow in reservoirs and is not applicable to oil/gas double-phase flow. The ratio of actual oil well production with the ideal oil well production under the same pressure drop was used to define the flow efficiency and a new productivity prediction equation of partially penetrated well was established. The calculation result of this equation was verified by the results of reservoir numerical simulation.
Key words:solution gas drive reservoir; partially penetrated well; productivity equation; Standing equation; IPR Curve; flow efficiency
作者简介:任宗孝,1989年出生。2013年硕士毕业于中国石油大学(北京),现为中国石油大学(北京)石油工程学院博士研究生,主要从事采油工程理论与技术方面的研究。E-mail:0789appleren@163.com。
基金项目:北京市自然科学基金青年科学基金“粗糙壁微型水平井筒气液两相流动机理研究”(编号:3154039)。
doi:10.13639/j.odpt.2015.05.017
文章编号:1000 – 7393(2015)05 – 0068 – 05
文献标识码:A
中图分类号:TE341

