新疆库车县城镇地下水资源污染迁移解析模型研究

李白业，李雪妮

(新疆地矿局第一水文工程地质大队，新疆乌鲁木齐830091)

近几年来库车县工业迅速发展，当地经济持续增长，地表水与地下水的需水量大幅度增加，废污水的排放及处理面临巨大的压力。要控制地下水的污染，保护地下水资源，就必须了解地下水现状污染的程度，预测将来可能影响的范围。在现状污染调查与评价基础上对研究区典型地段地下水中的特定污染组分浓度随空间与时间的变化进行计算预测，以掌握地下水污染的空间变化规律及发展趋势，以备及时有效地采取防控措施，有预见地减少污染危害。

1 预测方法的选用

地下水污染物迁移(见图1)模型研究是在现状污染调查与评价基础上对研究区典型地段地下水中的特定污染组分浓度随空间与时间的变化进行计算预测，以掌握地下水污染的空间变化规律及发展趋势，以备及时有效地采取防控措施，有预见地减少污染危害。本次计算典型地段选择新老城区及工业园区两个区段;预测单源污染液连续渗入在饱水带形成的污染晕(也称为弥散带范围)发展趋势及在未来30年对下游地段地下水的影响。

图1 地下水中污染物运移示意图

通常，地下水污染的预报分析可细分为定性分析、半定量分析及定量分析三种类型，以后者的分析精度最高，但分析精度越高对资料序列的要求也相应越高，野外投入也越大。水质污染定量预报模型可分为黑箱模型和灰箱模型。灰箱模型以地下水水动力学方法为主，方法主要包括简单的解析模型、半解析模型、数值模型。其中，数值模型法要求有长序列的特定组分监测资料和足够的野外弥散试验参数值，加上计算工作量繁重，多在环评一级或复杂条件的环评二级中使用。

地下水流态的非均质性，约束了常规解析法的应用范畴，盲目使用会产生很大误差[1]。计算机技术的广泛应用为解析法的改进提供了有力的条件，借鉴地下水水量数值模型中潜水的非线性问题(导水系数T随含水层厚度变化，呈现动态参数特征)的迭代处理办法，在解析计算中增加一个外部迭代过程，采用追赶法计算地下水非均质参数(称动态参数，如渗透系数 k=f[kx，x])，使参数域无限逼近污染晕锋面，这种方法可称为改进的解析模型方法。

综上，本次工作采用:定量分析方法→灰箱模型→地下水水动力学方法→改进解析法→适用于非均质条件的:改进的一维解析模型方法。

2 数学方程

有限宽度、无限长度，存在源汇项及综合作用，无边界的一维均匀稳定流孔隙渗流溶质运移偏微分方程或泛定方程式[2]通常可以表示为:

式中:C为溶质浓度，[ML－3];v为在渗流方向的平均地下水孔隙流速，[LT－1];D为纵向的弥散系数张量，[L2T－1];C'为源汇项中的溶质浓度，[ML－3];W'为源汇项流量，[M3T－1];n为有效孔隙度，[无量纲];K为水力传导系数张量，[无量纲];Rk为离子交换反应、分解反应、化合反应等的溶质生成量，[ML－3];x为笛卡尔坐标中渗流方向，[M];i，m为溶质综合反应的序次及总数。

公式(1)中的第一项代表水动力弥散分量，第二项代表对流分量，第三部分多代表(源)汇项作用分量，第四项代表其它综合物理化学(降解)作用量如:离子交换、分解作用、沉淀作用及放射性衰变等分量。

以上方程中仅考虑污染物直接作用于饱水带的情况，实际上污染物在通过包气带时，由于吸附等温作用影响使溶质的迁移与饱水带水的渗流速度产生差异，出现迟滞现象。根据Grove[1976]的意见，考虑平衡控制的离子交换反应，将上述通用表达式变形后得到考虑吸附等温影响滞后作用，存在其它作用(包括分解，化合及放射性衰变等)但无源汇项时的一维流水质运移偏微方程式为:

其中:R为阻滞系数，[无量纲];μ为综合作用一阶系数，当存在某种作用时反演求得;γ(x)为综合作用零阶系数，与空间坐标有关，亦在反演时求得。

3 建模步骤与解算方法

3.1 建模步骤

建模步骤见右侧的流程框图(见图2)。

图2 解析模型法建模步骤流程框图

3.2 解算方法

本次工作经筛选采用中美环保科技交流推荐的软件包STANMOD 2.1(STudio of ANalytical MODels，1999 年)，这是一个WINDOWS－XP图形界面软件包，整合了包括CXTFIT[Toride et al.，1995]在内不同解法的几个一维流及二维流解算模型，本次计算选用的CXTFIT模型算法[3]是由美国盐渍土实验室研制的，逆计算基于列文伯格－马夸尔特法(Levenberg－Marquardt算法[4]，简称LM算法)对均质一维稳定流动中溶质易混合置换实验所得到的穿透曲线(Breakthrough curve，BTC)进行非线性最小二乘拟合对偏微分方程进行解算的。该算法是高斯－牛顿法和梯度下降法的结合，既有高斯牛顿法的快速、也有梯度下降法的全局搜索特性[5]。

4 模型参数

模型参数包括实测参数和经验参数两部分。主要实测参数包括:污染源下游带水流方向的含水层参数(K－平均渗透系数、n－平均有效孔隙度、I－平均水力坡度)，污染源示踪组分的迁移速率Vc及平均浓度C0;经验参数主要包括:DL－纵向弥散度，R－阻滞系数。

其中，地下水参数宜采用动态平均加权值，权重采用污染晕过境参数区的值径向长度(注:二维流一般采用的是参数分区面积)。参数分区则采用本次水量数值模型分区成果。

地下水动态平均参数计算公式为:

4.1 平均渗透系数(K)

平均渗透系数为动态地下水实测参数，参数分区及参数值采用本次水量数值模型的参数分区成果;权值采用平水位期的地下水等水位线图进行图解量算。根据公式(3)，参数计算结果见表1。

表1 平均渗透系数K(m/d)计算一览表

4.2 平均水力坡度(I)

在地下水等水位线图上，对径向的水力坡度进行分段图量计算，径向水力坡度计算的起点为污染源处，终点为污染晕锋面位置。计算公式为I=△H/L，计算结果见表2。

4.3 有效孔隙度(n)

在没有进行弥散试验时，有效孔隙度主要用来将参与地下水实际流速的计算，由于地下水孔隙度变化多依赖于含水层岩性，变化幅度也较K值小的多，因此，采用在水量数值模型计算中其分区范围与数值。延用动态渗透系数计算办法，根据公式(3)计算的各平均有效孔隙度值见表3。

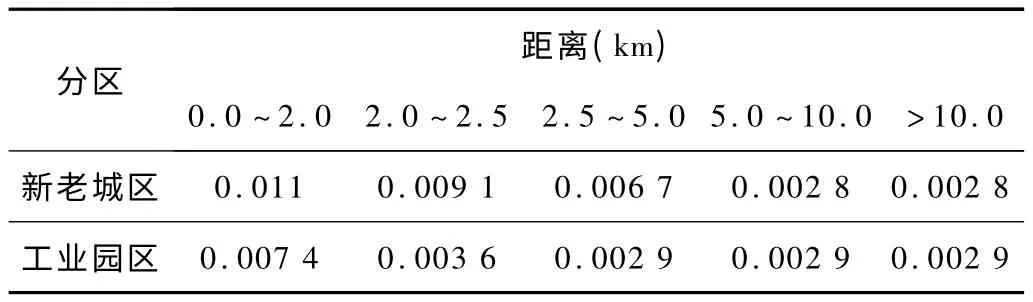
表2 平均水力坡度I计算一览表

表3 平均有效孔隙度n计算一览表

4.4 纵向弥散度(DL)

根据中国地质大学教授马腾等的论著[6]，世界上越来越多的室内外弥散试验不断地证实了空隙介质中水动力弥散具有尺度效应。一些研究者综合世界范围内百余个水质模型中所使用的纵向弥散度与空间尺度的关系，认为水动力弥散的尺度效应具有分形特征，同时，还给出了不同模型纵向弥散度尺度效应的分维数。根据分维数和空间尺度可以按经验公式计算出适合的弥散度参数初值(见表4、表5)。

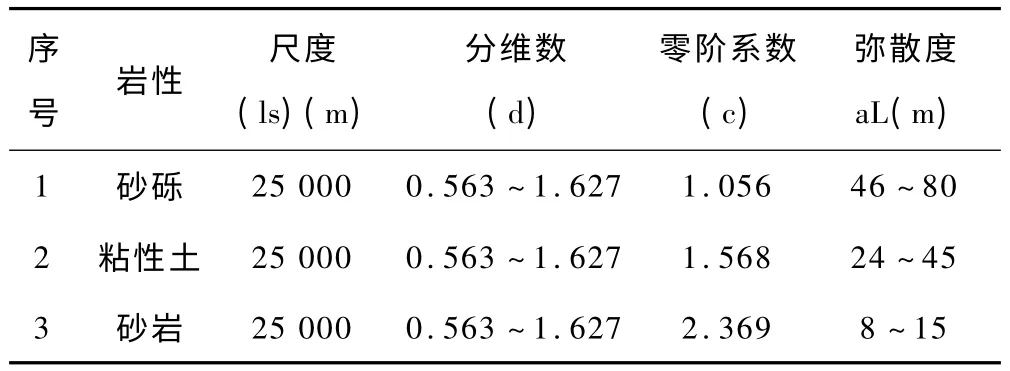
表5 不同岩性条件下的弥散度初值aL计算结果表

4.5 阻滞系数(R)

该参数反映了污染迁移速度与地下水流动速度之间的差异[7][8]，不同污染因子在不同岩性环境条件下的迁移速度有很大的差别，但当污染因子与污染物整体运移差异不大时，这种滞后作用就不明显了。一般试验测定[8]的粘土类的阻滞系数为2，～5砂土类多在1.0～1.2之间，砂砾石类就更小了，因此本次工作采用1.0～1.5的经验值范围作为阻滞系数初值，如有可能就在模型参数识别时根据现状污染趋势进行适当的修正。

5 计算结果

预报的起始位置在依巴格－乌恰镇的铁路沿线附近，这里也是城市污水处理场所在的位置。预报模型的时间以5年为间隔，共预报30年。根据曲线判别出每年污染晕移动的位置。新老城区30年末污染晕峰面到达下游8.0 km外的牛场－喀鲁乌古一带南3km农业区，前峰带宽度近400 m，累计污染物容量为8 026.17 C0×B×M(B为污染带宽度，M为污染含水层厚度)。工业园区污染峰面30年末到达5.7 km的西水东调干渠一线，前峰带宽度近300 m，5 154.84 C0×B×M。

6 结语

本次工作利用国际标准化一维流水质运移软件包，采用改进的解析法对下游地下水污染迁移问题进行研究，在新疆地下水研究中尚属首次。改进的一维流解析法提高了计算精度，完全适用于非均质流条件，选用方法符合环评二级要求。因监测资料缺乏，模型识别略显粗糙，影响污染晕弥散范围的预测精度，但在以对流为主的污染迁移中，对污染晕向下游的运移距离影响误差可以接受。计算结果仅可用于下游污染影响带地下水开采规划决策参考，不能作为污染治理专项设计及水事纠纷处理的法律依据。

[1]薛禹群，谢春红.地下水数值模拟.北京:科学出版社.2007.

[2]I.Javandel，C.Doughty，等著.林学钰，李生彩，等译.地下水运移数学模型手册.长春:吉林科学技术出版社.1985.

[3]N.Toride，F.J.Leij，and.The CXTFIT code for Estimating Transport Parameters from Laboratory or Field Tracer(Version 2.1).U.S.:SALINITY LABORATORY AGRICULTURAL RESEARCH SERVICE AND DEP ARTMENT OF AGRICULTUGE RIVERSIDE CALIFORNIA.1999.

[4]Marquardt，D.W.，An algorithm for least－ squares estimation of nonlinear parameters ，J.soc.ind.appl.Math.，11，431 －441，1963.

[5]袁亚湘，孙文瑜.最优化理论与方法.北京:科学出版社.1997.

[6]马腾，王焰新.“地下水污染与防治”课程建设的思考与实践.大学环境类课程报告论坛论组委会编.大学环境类课程报告论坛论文集(2006).北京:高等教育出版社，163－166.

[7]石振华，李传尧，等.城市地下水工程与管理手册.北京:中国建筑工业出版社.1993.

[8]Bruce E.Rittmann，Perry L.Mccarty，等著.文湘华，王建龙译.环境生物技术原理与应用.北京:清华大学出版社.2004.