新型CPU散热器内空气流动与换热特性的数值研究
伊丽娜,郑文龙,王博杰,王文
(上海交通大学制冷与低温工程研究所,上海 200240)
新型CPU散热器内空气流动与换热特性的数值研究
伊丽娜*,郑文龙,王博杰,王文
(上海交通大学制冷与低温工程研究所,上海 200240)
针对应用于电子芯片的矩形通道翅片散热器换热性能的不足,提出了一种新型打断翻折型翅片散热器,并对两种散热器单通道内的流动换热进行CFD数值模拟。本文综合分析了f、j、无量纲因子(j/f)1/3和δ等参数,证明了打断和翻折翅片可以减薄边界层厚度、促进流体扰动和强化对流换热的效果。根据场协同理论和广义温度梯度均匀化原则,深层挖掘强化换热的内在规律;证明新型结构优于矩形结构,为用散热器冷却电子芯片提供了参考。
CPU芯片;对流换热;数值模拟;场协同理论
0 引言
据调查,CPU芯片的功率每36个月翻一番[1];调查表明,55%的CPU失效都由过热引起[2]。因而电子器件散热与冷却成为国内外学者竞相研究的课题。
一方面,对于矩形结构或平板翅片结构,主要对散热器的结构参数(翅片厚度、间距、布置方式)和材料等进行优化研究。例如:MALHAMMAR A[3-5]研究了芯片表面和环境之间的温度差、翅间距、翅片厚度和空气来流速度等参数对平板翅片散热器的散热量的影响;胡艳等[6]运用CFD软件FLUENT对等截面直肋散热器在侧送风对流换热方式下,不同肋厚、肋高和肋间距的温度场进行数值模拟,得出了一组具有最优参数的散热器;徐博等[7]基于ε-NTU方法,分析了翅片参数对换热性能和成本的影响。另一方面,针对平板翅片式散热器存在的不足,其它翅片结构形式的分析层出不穷。LEE S[8]对39组锯齿型翅片进行了数值模拟,发现摩擦因子f对Pr数不敏感,而传热因子j的值与Pr数相关;陆正裕等[9]研究对整体平直翅片与分段式的平直翅片,在不同加热功率、不同流速下的强迫风冷的传热性能进行了实验研究,实验结果表明分段式翅片散热性能更好,其换热系数随流速的变化可达到整体平直翅片的两倍;余小玲等[10]分析了一种翅片间设有钉柱的翅柱复合型散热器,结果表明,在相同的散热量和风速下,复合型散热器的热阻小于矩形翅片散热器,前者比后者降低10%~20%。另外,向熠等[11]对雷达平板箱型天线阵面的散热器在封闭空间内的结构进行了优化分析,为小空间电子散热的优化设计提供了参考。
场协同理论方面,何雅玲[12]提出场协同原理不仅适用于抛物形流动,同样适用于椭圆形流动;王娴等[13]通过分析场协同数来对比对流换热效果,场协同数越大,说明速度场与温度梯度场的协同性越好;黄维等[14]分析了温度梯度与速度矢量的夹角对矩形翅片椭圆管换热特性的影响。
这些研究主要分析结构对称的散热器,在不同流速下的传热性能,本文提出一种新型非对称打断翻折型散热器,从实际运行特征出发,采用周期性边界条件,风扇入口进行数值模拟分析,研究其与传统矩形结构散热器流动与换热的异同。
1 数值模拟
1.1 物理模型
图1为矩形散热器和新型打断翻折型散热器单通道的结构示意图,图2为新型结构单元体后半部分示意图,几何尺寸如表1所示。

图1 矩形单通道(左)、新型单通道(右)示意图
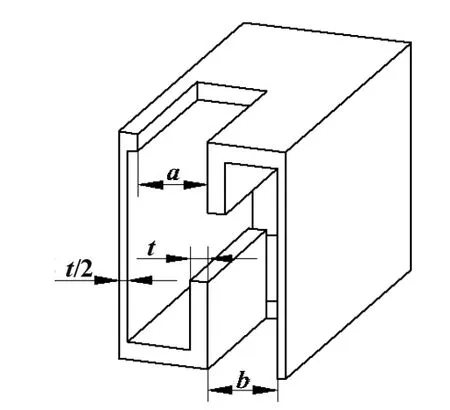
图2 新型结构单元体后半部分示意图
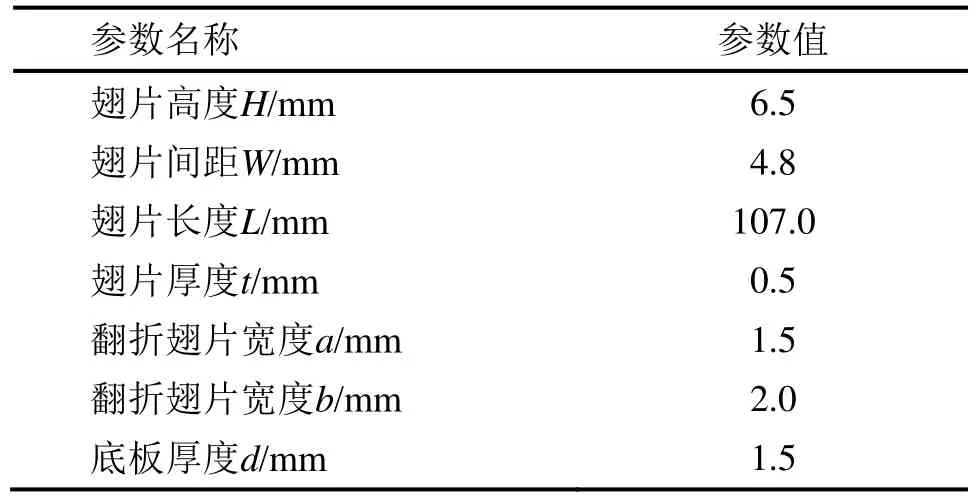
表1 散热器单通道的几何参数
在矩形散热器单通道的基础上,将其沿流道方向打断,段长为19 mm,段间距为3 mm,得到5段单元体。每个单元体上下表面分别在中间位置取长为9 mm、宽分别为a和b的矩形翅片,将其向通道内翻折,得到新型打断翻折型散热器单通道。
本文将对这两种散热器单通道内的流动和换热进行数值计算。
1.2 计算区域及计算方法
由于散热器各个通道内的流动状况基本相同,在两种散热器中各取一个通道为计算区域。将入口边界设置在通道上游距离入口1/5 L(L为翅片长度)的位置,出口边界设置在通道下游距离出口1 L的位置,以满足无回流的边界条件[15]。散热器单通道上方3 mm所在平面为计算区域的上界,底板的下表面所在平面为计算区域的下界。计算区域的两个侧面为翅片的周期对称面。假设通道内的流动为三维、稳态、不可压的层流流动。选用双精度求解器和SIMPLEC算法;动量、能量控制方程均采用Second Order Upwind离散格式;采用结构化网格,模型网格数为120万以上。在求解过程中,当连续性方程、动量方程和能量方程中变量残差均小于1.0×10-6且不发生变化时,认为计算收敛。
1.3 边界条件
进口边界:风扇入口。
出口边界:压力出口。
侧面边界:周期性边界条件。
壁面边界:底板的底面上设定均匀热流密度为6,840 W/m2。
散热器和底板的材料均为铝,进口空气温度为21 ℃,设定材料的特性参数均不随温度变化。
2 计算结果与分析
2.1 整场分析
2.1.1 通道内速度场和温度场分析
图3为矩形结构和新型结构沿流通轴向截面温度云图。此截面切割上部翻折翅片对应的窗口,同时也是下部翻折翅片的对称中心。从图中可见,新型结构整场温度低于矩形结构,是由于翻折翅片有效的将底板的热量传导至肋片上,进而促进与通道内的流体的对流换热,提高换热效率;另外,新型结构的均温性更好,利于对流换热,详细原因见下文2.2.3广义温度梯度均匀化。

图3 两种结构温度云图(单位:K)
图4为矩形结构和新型结构速度矢量图,截面位置与图3一致。对比二者的速度矢量图,可知新型结构打断翻折翅片,使得其扰动明显增加,促进对流换热。
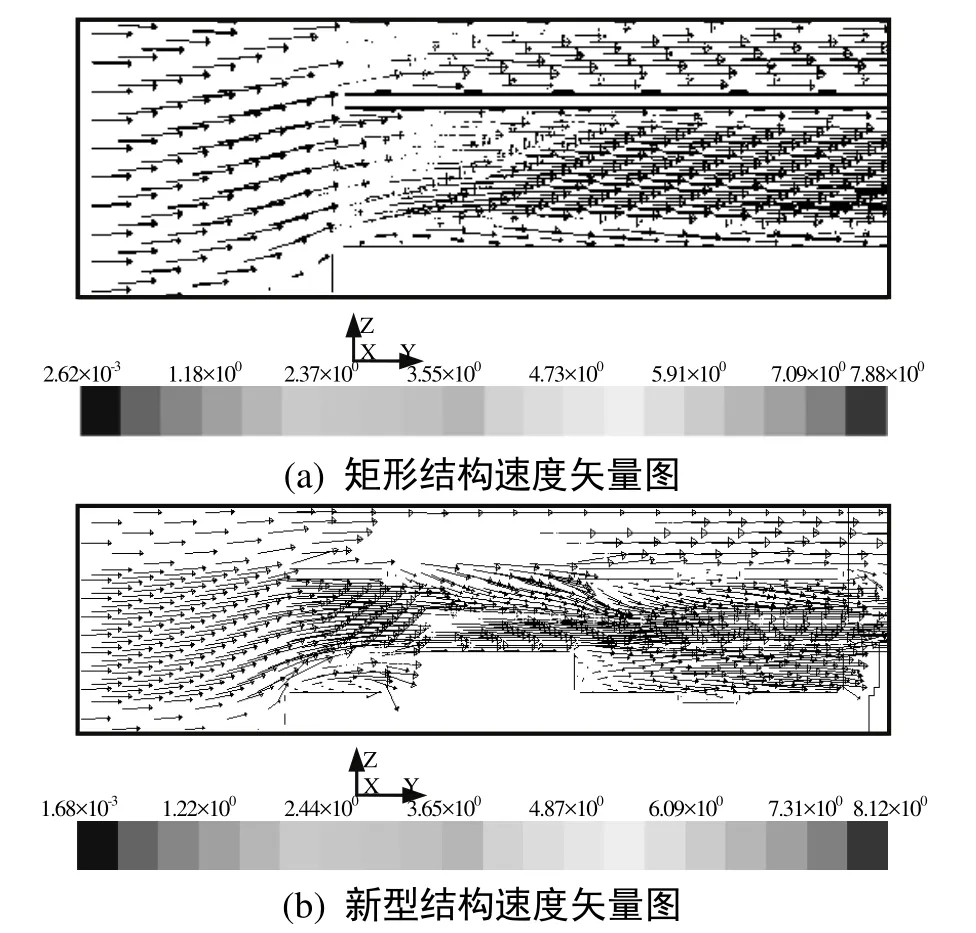
图4 两种结构速度矢量图(单位:m/s)
2.1.2 通道内的流动和换热分析
由数值模拟得到的数据,可以分别通过计算得到翅片的摩擦因子f和传热因子j。
据文献[16],摩擦因子f的定义方程为:

传热因子j的定义方程为:

式中:
L ——通道长度,m;
Dh——水力直径,m;
ΔP——通道压力降,Pa;
ρ——流体密度,kg/m3;
Re ——雷诺数;
Nu——努赛尔数;
Pr——普朗特数。
在相同风扇入口的边界条件下,得到两种结构流动和换热参数对比的结果,如表2所示。底板温度的高低决定了实际散热器所在位置芯片温度的高低,这是电子冷却的核心问题。由表2可知,新型结构和矩形结构底板温度最高值分别为336.5 K和350.7 K,同时,前者j因子高于后者,说明新型结构的换热效果明显优于矩形结构。然而,换热的增强也带来阻力的增大,新型结构的f因子高于矩形结构,因此,应综合考虑流动和换热的效果。二者的无量纲因子(j/f)1/3分别为0.343和0.356,新型结构的(j/f)1/3因子大于矩形结构。综上所述,新型结构的整体换热效果优于矩形结构。

表2 两种结构流动和换热参数对比
2.2 单元体分析
从边界层与场协同理论对两种换热器进行分析。由于新型结构5段单元体的结构相同,换热规律相似,故分析第一段单元体为例,矩形结构取相同位置与之对照。
2.2.1 边界层分析
在散热器的入口,分别取矩形结构通道下表面和新型结构向上翻折肋片的侧面,如图5阴影面所示。对这两个阴影面沿流道方向进行边界层厚度的分析,结果如图6所示。
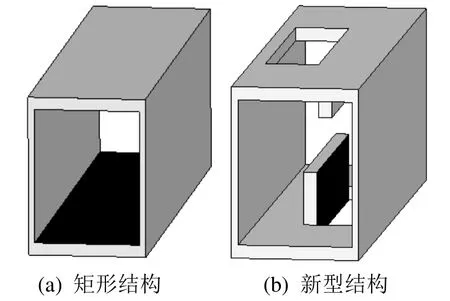
图5 两种散热器单通道入口示意图
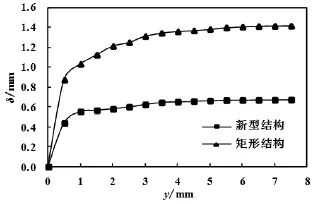
图6 两种结构的边界层厚度
对比矩形结构和新型结构阴影面所在位置的边界层厚度,前者约为后者的二倍,定性地说明了打断翅片有减薄边界层的作用。同时,打断翅片也使得沿着流通方向的边界层重新发展,有利于充分发挥入口效应,强化换热。
2.2.2 场协同分析
对于对流换热过程,过增元[17]提出场协同理论,指出换热强度不仅取决于流体的速度和物性,而且取决于流速与热流矢量的协同,对流换热强化要求速度矢量和热流矢量之间相互协同。基于此理论对两种结构的协同角进行分析,内容如下:
由文献[17]可得公式:
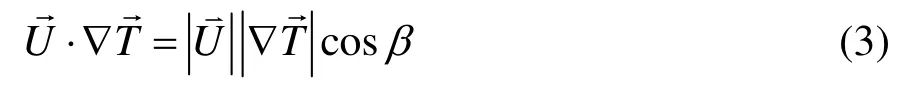
则:
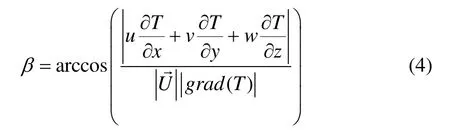
当夹角β小于90°时,β愈小则对流换热系数愈大,达到其最大值。
图7是风扇入口条件下,矩形结构和新型结构单通道内,轴向上的一条直线对应速度与温度协同角的变化。可以看出,第一,在轴向0 mm~5 mm处,矩形结构和新型结构协同角迅速升高,原因在于风扇入口距离通道入口为1/5 L,由于流通面积和通道阻力的影响,空气不是水平,而是斜灌入通道内,因此,通道入口处协同角较小,而进入通道后,受到通道壁面的束缚以及风扇沿着轴向的推动作用,速度更趋于平行于轴向,使得协同角升高。第二,轴向距离大于5 mm时,矩形结构的通道结构不变,其协同角趋于平稳,而新型结构的通道结构沿着轴向不断变化,通道上部空间的空气从通道上表面的翻折处和两个单元体之间的打断处,不断与通道内的空气混合、扰动,使得协同角波动幅度很大。整体来讲,对比矩形结构和新型结构的协同角,二者协同角的均值分别为88.12°、87.76°。新型结构的协同角更小,根据场协同理论,新型结构更有利于换热。
总之,翅片翻折后,空气的扰流作用增强,使得速度与温度的协同角降低,强化了换热。
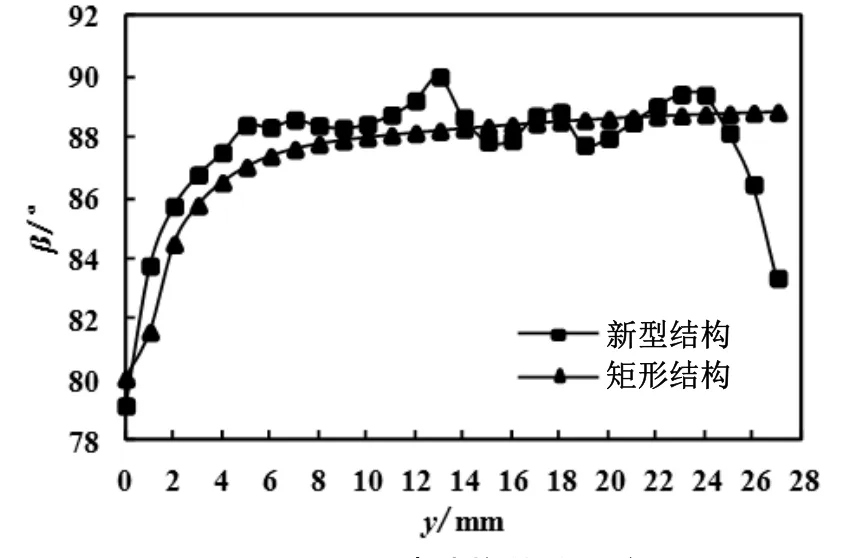
图7 两种结构的协同角
2.2.3 广义温度梯度均匀化分析
基于过增元提出的场协同原理,夏再忠[18]提出换热过程的仿生优化理论,证明了广义温度梯度均匀化原则(即|W|最小原则)是强化对流换热的基本规律。
式中:A为逆温度。
对两种结构沿轴向流通截面的W进行分析,结果如图8所示。由图8可知,新型结构的|W|明显小于矩形结构,说明新型结构轴向流通截面的温度场更均匀。同时,上文图3温度场的云图也揭示了新型结构温度场更趋于均匀这一事实。而此均匀性是翅片翻折带来空气的混合与扰动的必然结果。
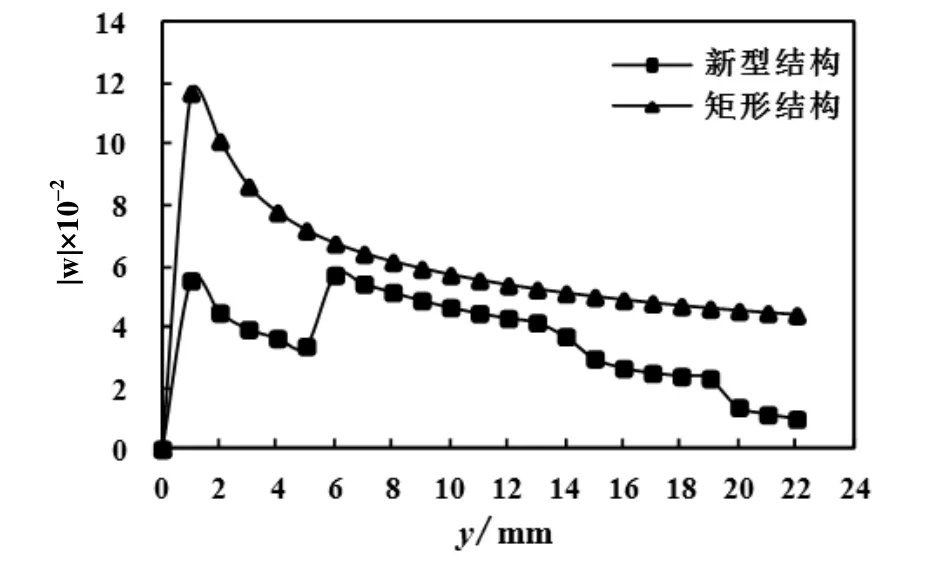
图8 两种结构的|W|
3 结论
通过对矩形结构与新型结构的CFD数值模拟分析,得到以下结论。
1)分析两者数值模拟结果,发现新型结构打断与翻折的设计使得扰动增加,更有利于换热与整场温度的均匀化。
2)综合分析Tmax、f、j和无量纲因子(j/f)1/3等参数。新型结构的底板温度与矩形结构相比低了14.2 ℃(分别为336.5 K和350.7 K),说明新型结构的整场换热效果更加理想。新型结构的f、j因子均大于矩形结构,说明强化换热的同时,阻力也相应增加。二者的无量纲因子(j/f)1/3分别为0.356和0.343,新型结构的(j/f)1/3因子大于矩形结构,因此前者整体散热器性能要优于后者。
3)分析单元体边界层厚度,定性地证明了打断和翻折翅片减薄了边界层,促进边界层重新发展,充分发挥入口效应,强化换热。
4)从场协同原理与广义温度梯度均匀化原则角度出发,分析了新型结构和矩形结构的换热器性能,发现新型结构换热器性能优于矩形结构。
[1] MAHAJAN R, NAIR R, WAKHARKAR V, et al. Emerging directions for packaging technologies [J]. Intel Technology Journal, 2002, 6(2): 62-75.
[2] IWASAKI H, ISHIZUKA M. Forced convection air cooling characteristics of plate fins for notebook personal computers[C]// Thermal and Thermomechanical Phenomena in Electronic Systems, 2000. ITHERM 2000. The Seventh Intersociety Conference on IEEE, 2000: 21-26.
[3] MALHAMMER A. Optimization of heat sinks in non-confined flow[EB/OL]. [2002-12-31]. http://www. coolingzone.com/library.php?read=538.
[4] MALHAMMER A. Optimization of heat sinks in confined flow[EB/OL]. [2005-12-31]. http://www. coolingzone.com/library.php?read=537.
[5] MALHAMMER A. Heat sinks and reynolds analogy[EB/OL]. [2005-12-31]. http://www.coolingzone. com/library.php?read=536.
[6] 胡艳, 郭广思, 尚新泉, 等. CPU散热器数值模拟分析[J]. 低温与超导, 2009, 37(9): 60-65.
[7] 徐博, 祁照岗, 陈江平, 等. 微通道换热器翅片参数研究[J]. 制冷技术, 2011, 31(4): 16-20.
[8] LEE S. Optimum design and selection of heat sinks [J]. IEEE Transactions on Components, Packaging, and Manufacturing Technology: Part A, 1995, 18(4): 812-817.
[9] 陆正裕, 熊建银, 屈治国, 等. CPU散热器换热特性的实验研究[J]. 工程热物理学报, 2004, 25(5): 861-863.
[10] 余小玲, 冯全科, 冯健美, 等. 高效翅柱复合型散热器的流动与散热性能研究[J]. 西安交通大学学报, 2004, 38(11): 1114-1118.
[11] 向熠, 王勇. 平板箱型天线阵面的封闭式风冷散热结构设计[J]. 制冷技术, 2014, 34(4): 63-66.
[12] 何雅玲, 陶文铨. 强化单相对流换热的基本机制[J].机械工程学报, 2009(3): 27-38.
[13] 王娴, 宋富强, 屈治国, 等. 场协同理论在椭圆型流动中的数值验证[J]. 工程热物理学报, 2002(1): 59-62.
[14] 黄维, 赵兰萍, 茅文焯. 矩形翅片椭圆管束性能研究及场协同分析[J]. 制冷技术, 2009, 29(4): 29-32.
[15] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2005.
[16] 钟昌雄, 李蔚, 张文华, 等. 多区域开窗翅片的热力性能实验研究[J]. 机电工程, 2008, 25(7): 11-14.
[17] 过增元. 对流换热的物理机制及其控制:速度场与热流场的协同[J]. 科学通报, 2000, 45(19): 2118-2122.
[18] 夏再忠. 导热和对流换热过程的强化与优化[D]. 北京:清华大学, 2001.
Numerical Study on Flow and Heat Transfer Characteristics of Air in A New CPU Heat Sink
YI Li-na*, ZHENG Wen-long, WANG Bo-jie, WANG Wen
(Institute of Refrigeration and Cryogenics, Shanghai Jiao Tong University, Shanghai 200240, China)
Aiming at the insufficient heat exchange performance of rectangular channel fin heat sink for electronic chips, a new heat sink with interrupted and folded fins was proposed. Numerical simulations on the flow and heat transfer of air in single flow channel for the two kinds of heat sink mentioned above were performed. The parameters of f, j, dimensionless factor (j/f)1/3and δ were comprehensively analyzed, and the results show that interrupted and folded fins can make fluid boundary layer thickness thinner and promote disturbances, thus the convection heat transfer was enhanced. According to field synergy theory and generalized temperature gradient uniformity principle, the inherent laws of heat transfer enhancement was deeply excavated. The new structure is proved to be superior to the rectangular structure. Moreover, the result provides a reference to the design of heat sink for cooling the electronic chips.
CPU chip; Convective heat transfer; Numerical simulation; Field synergy theory
10.3969/j.issn.2095-4468.2015.01.109
*伊丽娜(1987-),女,在读硕士研究生。研究方向:制冷与低温。联系地址:上海市闵行区东川路800号,邮编:200240。联系电话:18818272642。E-mail:janeeyre246@163.com。

