ENSO预测的目标观测敏感区在热带太平洋海温的多模式集合预报中的应用
智协飞 张璟 段晚锁
1 南京信息工程大学气象灾害预报预警与评估协同创新中心/气象灾害省部共建教育部重点实验室,南京210044
2 南京信息工程大学大气科学学院,南京210044
3 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室(LASG),北京100029
1 引言
ENSO是重要的短期气候现象之一,它的发生、发展可引起全球性气候异常,造成众多地区发生严重的旱涝、高温或低温冰雪灾害,导致许多国家的工农业生产和人民生命财产遭受巨大损失(龚道溢和王绍武,1999;Wang et al., 2000;Trenberth et al., 2002;张人禾等,2003;Sakai and Kawamura,2009)。因此,对 ENSO事件乃至整个热带太平洋地区海温的准确预测具有重要意义。
在过去几十年里,关于ENSO的理论和数值模拟研究均取得了很大进展,但其预测结果仍呈现很大的不确定性(翟盘茂等,2003;Luo et al., 2008;Jin et al., 2008)。不同模式间的预测结果存在较大差异,这种差异可能是由模式内部框架和物理过程的处理方法,以及数值模式的初始化方案不同导致的,如模式的水平和垂直分辨率、物理参数化方案、初始场、资料同化技术等。考虑到各个模式预报均存在不确定性,多模式集合预报技术 得到了发展。多模式集合预报是一种能够提高模式预测水平的一种统计后处理方法(杨学胜,2001)。早在上世纪60~70年代,Danard et al.(1968)和 Thompson(1977)研究发现,通过将两个相互独立的预测结果进行特定的线性组合,其预测的均方根误差(RMSE)可以小于单个预测结果的预报误差。在此基础上,Krishnamurti et al.(1999,2000a)提出了超级集合预报方法(Superensemble Prediction,SUP)。该方法是将多个模式的预报结果通过选取适当的权重系数组合在一起,形成最终的预报结果,以此来降低模式的系统偏差对预报结果的影响。研究表明,SUP方法能够有效减小数值模式对天气和气候的预报不确定性(Krishnamurti et al., 2006,2009;智协飞等,2009,2013;Zhi et al.,2012)。
简单集合平均(Ensemble Mean,EMN)、消除偏差集合平均(Bias-removed Ensemble Mean,BREM)、回归改进集合平均(Regression-improved Ensemble Mean)及综合超级集合(Synthetic Superensemble,SSE)等多模式集合预报方法近年来也被广泛用于季节气候预测(Peng et al., 2002;Yun et al., 2005;Kang and Yoo,2006;Ke et al., 2009;Min et al., 2009;Yatagai et al., 2014)和年际气候预测(van Oldenborgh et al., 2012;Johnson et al.,2013),其中SUP和BREM方法为最具代表性的两种方法。针对这两种方法,以往研究结果认为,SUP方法的平均预报技巧高于 BREM(Krishnamurti et al., 2000b,2007),但SUP方法需要逐个格点计算模式权重,相对于简单的等权重BREM方法,计算量较大,尤其体现在高分辨率模式中(Chakraborty and Krishnamurti,2006;Cartwright and Krishnamurti,2007)。
目标观测是近一二十年兴起的一种新的观测策略,它意图在一个小范围的关键区域内增加观测,并将这些额外观测同化到初始场,使其与大范围增加观测对预报技巧有同等或相当的改善程度(Lorenz and Emanuel,1998;Mu,2013;周菲凡和张贺,2014)。这个小范围的关键区域通常称之为目标观测敏感区,识别该关键区域的理论依据是数值模式的预测结果对该区域内的初始误差最敏感。Duan et al.(2009)和 Mu et al.(2007)用中等复杂程度Zebiak-Cane模式(Zebiak and Cane,1987)研究ENSO可预报性的结果表明,热带太平洋海温预测的初值敏感区位于赤道中东太平洋。Zhang et al.(2014)进而用CMIP5模式资料验证了该区域的敏感性。此外,Duan and Zhao(2014)的研究表明热带太平洋海温的预测对于上述区域的模式误差也是最敏感的,即在热带太平洋SST预测中该区域的初始误差和模式误差对于ENSO预测的不确定性均有最大贡献。因此,为了减小热带太平洋海温的预测不确定性,提高预报技巧,应该优先减小目标观测敏感区内的初始误差和模式误差。
多模式集合预报可以有效减小模式不确定性的影响,但集合中的每个模式成员具有不同的初始化方案,因而具有不同的初值。因此,多模式集合预报也能够在一定程度上减小初始误差的影响。试想,如果只在上述目标观测敏感区内使用具有较高预报技巧的集合预报方法(如SUP方法等),而在预报结果对误差相对不敏感的区域使用简单的集合方法(如 EMN、BREM 方法等)来减小模式误差和初始误差的影响,可能与大范围使用计算量大的高技巧方法(如 SUP方法)对预报的改进效果相当,但前者可以大大减少计算成本。为检验上述推理,本文将ENSO预测的目标观测敏感区与多模式集合预报方法相结合,针对热带太平洋SST进行预测研究,从而尝试提供一种能够有效提高预报技巧且又具有较小计算成本的多模式集合预报方法。
2 超级集合预报方法和消除偏差集合平均方法
SUP与BREM方法均是对多个模式的模拟结果进行后处理以获得最佳预报效果的统计方法。SUP方法将时间序列分为两部分,包括训练期和预报期。在训练期对各模式模拟资料和观测资料(或再分析资料)进行训练建模,确定参与集合的各模式预报结果的权重系数,根据该权重系数,在预报期对集合成员进行不等权集合平均,得到集合预报结果。具体预报模型由(1)式构建,在一个给定的格点上,对于某一气象要素有

其中,St为第t时刻超级集合预测值,为训练期观测值的平均,Fi,t为第i个模式第t时刻的预报值,为第i个模式在训练期的模拟值平均,ai为回归系数(权重),t为预报时刻,n为参与集合的模式总数。回归系数ai由下式中的误差项G最小化计算而得:

其中,’为第t时刻观测值的距平,St’为第t时刻SUP集合值的距平,Ntr为训练期长度。应用最小二乘法原理使训练期中误差G最小,以此来确定参与集合的各模式权重ai。最后将各个模式相应的权重代回(1)式,来进行模式不等权集合预报。此外,(1)式中可以看到,SUP方法中引入观测场气候态O来代替预报气候态,同时各个模式的加权是叠加在模式预报异常场上,因此能够最大程度减小模式气候漂移及模式偏差。
BREM方法计算过程与SUP基本类似,但其不需要逐点确定模式权重系数,只需取为1/n(n为参与集合的模式总数)即可,因此为等权集合方法,计算量较小。具体算法由下式定义:
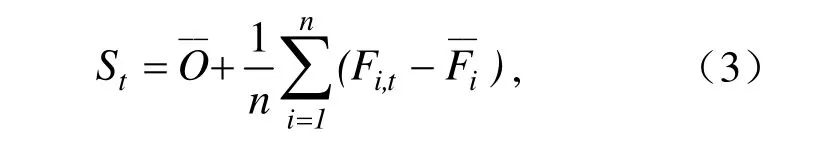
式中其余变量定义与(1)式相同。
关于SUP和BREM方法集合效果的比较,大部分研究认为不等权 SUP方法的预报技巧整体上高于等权重BREM方法。我们针对热带太平洋地区SST的多模式集合预报的试验中,也得到了类似的结果。但是 SUP方法需要逐个点计算各模式权重,计算过程相对复杂,耗时。尤其是当模式分辨率较高或是预报更大范围更长时间尺度时,计算成本将远远大于 BREM 方法,这在前人的研究中也多次提到(Chakraborty and Krishnamurti,2006;Cartwright and Krishnamurti,2007)。鉴于两者各自的优点(表1),我们试图发展一种新的集合预报方法,从而将两种集合方法的优点结合,即提出一种能够有效提高预报技巧且又具有较小计算成本的多模式集合预报方法。

表1 超级集合预报方法(SUP)和消除偏差集合平均方法(BREM)比较Table 1 Comparison of the superensemble prediction (SUP) and bias-removed ensemble mean (BREM) methods
3 目标观测敏感区与多模式集合预报方法的结合
如引言所述,只在ENSO预测的目标观测敏感区内使用计算量大的高预报技巧的集合方法,而在预报结果对初始误差和模式误差不敏感的区域使用较为简单的集合方法,其预报技巧可能与整个区域使用高技巧集合方法的预报效果相当,然而前者可以大大减少计算成本。针对热带太平洋 SST预报,本文将利用上述思路将ENSO预测的目标观测敏感区和多模式集合预报相结合,形成一种新的“目标观测敏感区—多模式集合预报方法”。如图1所示,将热带太平洋地区(15°S~15°N,150°E~90°W)等分为6个子区域,其中第4子区域为Duan and Wei(2013)和Mu et al.(2013)研究表明的热带太平洋SST预报的目标观测敏感区。对于“目标观测敏感区—多模式集合预报方法”,我们是在第 4区域使用具有较高预报技巧但比较费时的 SUP方法,而在其他不敏感区域使用相对简便快捷却预报技巧较低的BREM方法。为方便,将该预测方案用记号“SUP(4)+BREM(1-3,5-6)”表示。本文将通过对比以下预测方案来阐明“SUP(4)+BREM(1-3, 5-6)”预测方案在预报理想的热带太平洋SST长期演变中的有效性。具体预测方案如下:
(a)热带太平洋(15°S~15°N,150°E~90°W)统一采用多模式超级集合预报方法(SUP);
(b)热带太平洋(15°S~15°N,150°E~90°W)统一采用消除偏差集合平均方法(BREM);

图1 热带太平洋区域划分为6个区域(其中第4子区域为ENSO预测的目标观测敏感区)Fig. 1 Six regions in the tropical Pacific Ocean, in which the 4th region is the sensitive area of target observation for ENSO forecast
(c)采用“SUP(k)+BREM(除k以外的其他区域)”方法(在区域k使用SUP方法,而在其他区域使用BREM方法)。
对于集合预报效果的检验,选取常用的距平相关系数(Anomaly Correlation Coefficient,ACC)和均方根误差(Root Mean Square Error,RMSE)指标。具体做法是:首先计算预报期内每个预报时刻的预报场与观测场的ACC和RMSE值,再将整个预报期内的每个预报时刻的结果进行平均,整体评估各种集合预报方法的表现。理论上,(a)方案应该具有最高的预报技巧,但计算量巨大;(b)方案简便快捷,但预报技巧较低。本文目的是重点考察结合了目标观测敏感区的“SUP(4)+BREM(1-3,5-6)”方案是否可以大大降低计算量,且具有与(a)方案相当的预报技巧。
4 结果
本文所用数据来自CMIP5中15个气候系统模式的工业革命前参照(pi-Control)试验结果(表2),利用热带太平洋SST的150年逐月资料,研究范围为 15°S~15°N,150°E~90°W。 由于每个模式的水平分辨率各不相同,采用气象中常用的双线性插值方法将 15个模式资料统一插值到相同水平分辨率的网格上(2.5°×2.5°)。为了考察“目标观测敏感区—多模式集合预报方法”的有效性,本文将上述15个模式中的任一模式的pi-Control试验结果作为理想“观测”资料,而其他模式的试验结果作为针对该“观测”的“预报”结果进行了多组多模式集合预报试验,得到了类似的结论。为简便起见,本文以FGOALS-g2模式结果作为“观测资料”,而其他 14个模式结果作为“预报资料”来对热带太平洋SST进行多模式集合“预报”试验为例,重点介绍针对新方法有效性检验的试验结果。
首先针对预报期长度为 1年的情形进行了试验。结果表明,新的集合预报方法“SUP(4)+BREM(1-3,5-6)”具有与SUP相当的预报技巧,同时计算量远低于SUP。进而,本文对于预报期长度为5年、10年和20年的情形也进行了试验。我们发现,新集合预报方法同样具有较高的预报技巧,而且在此情形下,尤其体现了新方法较小的计算代价。
需要指出的是,多模式集合预报方法是一项对资料的统计后处理技术。其中,参与集合的模式个数和训练期样本的长度均会影响预报效果(Kharinand Zwiers, 2002;智协飞等, 2010;Krishnamurti and Kumar, 2012)。因此,在利用多模式结果进行集合预报之前,需要确定最优模式个数和最优训练期长度,以保证集合效果最优。下面将给出 SUP和BREM方法的优化试验结果。

表2 15个CMIP5模式概况Table 2 Brief description of the 15 CMIP5 models used in this study
4.1 最优模式个数试验
首先,以预报期长度 20年为例,介绍最优模式个数试验。第一步,评估了 14个气候系统模式在训练期内对热带太平洋(15°S~15°N,130°E~90°W)SST的模拟效果。具体以ACC和RMSE为度量,各模式的模拟效果由好到差排序依次为:BCC-CSM1.1、IPSL-CM5B-LR、CNRM-CM5、HadGEM2-ES、GISS-E2-H、BNU-ESM、CanESM2、NorESM1-ME、MRI-CGCM3、MPI-ESM-P、INMCM4、CCSM4、CESM1(FASTCHEM)、GFDLESM2G。需要说明的是,因为理想试验中是将FGOALS-g2模式的模拟结果作为“观测”,因此与该模式模拟结果最接近的模式为最优。接下来,按照单个模式的模拟效果优劣,从好到差依次加入模式进行集合。图2中分别给出了预报期为20年时,SUP和BREM 方法的预报技巧随模式个数的变化。可以看出,SUP与BREM方法的预报技巧均随着 模式个数的增加而逐渐提高。一定模式个数后,技巧提高变缓并逐渐接近最优水平。这是由于试验中是按照单个模式模拟技巧的好坏来依次加入模式的,开始时,多个模式的平均作用消除了部分随机误差,使预报技巧得到提高;当模式个数增加到一定程度时,预报效果达到最高水平。但当多模式集合预报技巧达到最优后,随着模式个数的增加又会逐渐降低,这可能是由于后加入的模式本身 技巧偏低,继续加入反而会使得整体预报效果下降。基于此,我们将SUP方法的最优模式个数确 定为12个,即剔除上述14个模式中的CESM1(FASTCHEM)和GFDL-ESM2G模式。BREM 方法的最优模式个数为 11个,即剔除CCSM4、CESM1(FASTCHEM)和GFDL-ESM2G模式。接下来,在预报期长度为 20年的热带太平洋SST的多模式集合预报中,SUP和BREM方法将分别使用前12个和11个模式参与集合,以此来保证两种方法的集合效果。
对于其他预报期长度的最优模式个数试验,由于过程类似,本文由表3直接给出试验结果。可以看到,当预报期长度为1~20年时,两种方法所需的模式个数对预报时长没有明显的依赖性,最优模式个数大致为8~12个之间。
4.2 最优训练期长度试验
本节介绍最优训练期长度试验,我们也以预报期长度 20年为例。具体做法是将预报期固定后,训练期长度逐年增加,通过相应的预报技巧变化来确定训练期与预报期的关系。合适的训练期长度在保证集合预报效果的同时也避免了训练期样本过长所带来的不必要的计算量。图3给出了预报期长度为20年时,SUP和BREM方法的预报技巧随训练期长度的演变。可以看出,开始时SUP与BREM的预报技巧均随着训练期长度的增加而迅速提高,当训练期长度大于 20年左右之后,集合效果基本保持稳定。因此,我们认为SUP和BREM方法中,当预报期长度为20年时,训练期长度选取20~30年较为理想。

表3 不同预报期长度,SUP和BREM方法所需要的最优模式个数Table 3 The optimal model numbers of SUP and BREM methods for different forecast period
对于其他预报期长度的最优训练期长度试验,这里仅给出SUP方法所得到的结果,为便于计算,BREM方法的训练期长度与其保持一致。图4中可以看到,当预报期长度为1年、5年、10年和20年时,SUP方法所需要的最优训练期长度大约为3年、10年、10年和20年。也就是说,随着预报时效的延长,所需的最优训练期长度也相应增加。
4.3 “目标观测敏感区—多模式集合预报方法”的有效性检验
本节中我们将考察 SUP方法、BREM 方法以及6组“SUP(k)+BREM(除k以外的其他区域)”方法对热带太平洋SST的预报效果。通过不同集合方法的比较,重点对“SUP(4)+BREM(1-3,5-6)”方案的预报有效性进行检验。具体做法是通过计算预报期内每个预报时刻“预报场”与“观测场”的ACC和RMSE值,再将整个预报期内的各个预报时刻的集合结果进行平均,来整体评估不同集合方法的表现。图5中给出了预报期长度为1年、5年、10年和20年时不同集合预报方案的预报技巧。可以看到,SUP方法的集合效果明显好于BREM方法。此外,6组不等权与等权相结合的集合预报方案中,“SUP(4)+BREM(1-3,5-6)”方案对预报结果的改进最为明显。事实上,由于预报结果对目标观测敏感区内初始误差和模式误差最敏感,因此只对该敏感区(即试验4区)采用预报技巧更高的SUP方法来减小该区域的模式误差,而其他不敏感区域采用简便快捷的BREM方法,理论上能够有效提高预报技巧且与整个区域使用 SUP方法的预报技巧相当。从上述结果可以看出,本文的数值试验结果验证了这一推理,即6组不等权与等权相结合的集合预报方案中,“SUP(4)+BREM(1-3,5-6)”方案对预报结果的改进最为明显。
上述研究中我们得到,在考察的预报期长度内(即 1~20年),“SUP(4)+BREM(1-3,5-6)”方案平均预报技巧好于BREM方法,并且在几组不等权与等权相结合的方案中预报技巧最高,且与预报技巧最高的 SUP方法的预报效果最为接近。此外,“SUP(4)+BREM(1-3,5-6)”方法运算时间仅为SUP的1/4。也就是说,在敏感区采用不等权的SUP方法,而在预报结果对误差不太敏感的区域采用相对简便的等权BREM方法,可以在有效提高预报技巧的同时大大减少计算成本。
5 总结与讨论
本文尝试利用目标观测中“敏感区”思想作为理论指导,将SUP与BREM这两种多模式集合预报方法进行结合,以期在保证预报技巧的同时减少计算成本。通过不同预报期长度下SUP和BREM方法的前期优化试验以及对各种集合方案对热带太平洋SST的预报效果进行比较,得到了以下几点结论:
(1)在所考察的预报期长度内(即1~20年),SUP和BREM方法所需的最优模式个数大致为8~12个之间不等,其对预报时长没有明显的依赖性。
(2)随着预报时效的延长,SUP方法所需的最优训练期样本长度也相应增加。当预报期长度为 1年、5年、10年和20年时,相应的最优训练期长度依次为3年、10年、10年和20年。
(3)在所考察的预报期长度内(即1~20年),6组不等权与等权相结合的多模式集合预报方案中,“SUP(4)+BREM(1-3,5-6)”方案,即目标观测敏感区采用不等权SUP方法,而其余对初始误差和模式误差不敏感的区域采用相对简便的等权BREM方法对预报结果的改进最为明显,且与SUP的预报技巧最为接近,同时大大减少了计算成本。
综上所述,本文提出了目标观测敏感区与多模式集合预报相结合的预报方法,即在目标观测敏感区内采用高技巧但计算耗时的模式不等权 SUP方法,而在其他区域采用相对简单的等权的BREM 方法。结果表明,新方法与预报技巧最高的SUP方法的预报效果最为接近,但计算成本仅为SUP的1/4。该结果强调了热带太平洋SST预测不仅对ENSO目标观测敏感区内的初始误差最敏感,而且对该区域的模式误差也是极端敏感的。然而,这些结果均是理想预报试验结果,并未在实际预报至少在回报试验中进行验证。另外,新方法涉及的目标观测敏感区对于本文所选取的模式是有效的,那么对于其它模式是否有效,即是说,该方法的有效性是否具有模式依赖性。因此,接下来的工作中我们将针对实际观测资料的回报试验来进一步验证新方法的有效性。同时,我们还尝试将这一思路运用到业务预报所关心的风、降水等气象要素的预报中去,以期为业务预报提供新的有用的预报思路。

图2 预报期为20年时, 两种集合方法预报的热带太平洋SST的距平相关系数(ACC; 黑色线)和均方根误差(RMSE; 蓝色线):(a)SUP方法;(b)BREM方法。横轴为参与集合的模式个数Fig. 2 The Anomaly Correlation Coefficient (ACC) (black line) and RMSE (blue line) of SST forecasts over the tropical Pacific Ocean from two multi-model ensemble forecast methods as a function of the number of ensemble models: (a) Superensemble prediction (SUP); (b) bias-removed ensemble mean (BREM).The forecast period is 20 a

图3 预报期为20年时, 两种集合方法预报的热带太平洋SST的距平相关系数(黑色线)和均方根误差(红色线):(a)SUP方法;(b)BREM方法。横轴为训练期长度(单位:a)Fig. 3 The ACC (black line) and RMSE (red line) of SST forecasts over the tropical Pacific Ocean from two multi-model ensemble forecast methods as a function of the length of the training period: (a) SUP; (b) BREM. The forecast period is 20 a

图4 不同预报期长度,SUP方法所需要的最优训练期长度。横轴为预报期长度(单位:a)Fig. 4 The optimal length of the training period of SUP method for different forecast periods (the horizontal axis denotes the length of forecast period, units: a)

图5 预报期为1年、5年、10年和20年时,SUP、BREM方法以及二者相结合的6组多模式集合预报方案预报的热带太平洋SST的(a1-a4)距平相关系数和(b1-b4)均方根误差(横轴为不同的集合预报方法)Fig. 5 The SST forecast skills from SUP, BREM, and 6 sets of multi-model ensemble methods over the tropical Pacific Ocean: (a1-a4) ACC; (b1-b4) RMSE.The forecast periods are 1 a, 5 a, 10 a, and 20 a. The horizontal axis denotes different multi-model ensemble methods
(References)
Cartwright T J, Krishnamurti T N. 2007. Warm season mesoscale superensemble precipitation forecasts in the southeastern United States[J]. Wea. Forecasting, 22 (4): 873–886.
Chakraborty A, Krishnamurti T N. 2006. Improved seasonal climate forecasts of the south Asian summer monsoon using a suite of 13 coupled ocean–atmosphere models [J]. Mon. Wea. Rev., 134 (6): 1697–1721.
Danard M B, Holl M M, Clark J R. 1968. Fields by correlation assembly—A numerical analysis technique [J]. Mon. Wea. Rev., 96 (3): 141–149.
Duan W S, Liu X C, Zhu K Y, et al. 2009. Exploring the initial errors that cause a significant “spring predictability barrier” for El Niño events [J]. J.Geophys. Res., 114( C4), doi:10.1029/2008JC004925.
Duan W S, Wei C. 2013. The ‘spring predictability barrier’ for ENSO predictions and its possible mechanism: Results from a fully coupled model [J]. Int. J. Climatol., 33 (5): 1280–1292, doi:10.1002/joc.3513.
Duan W S, Zhao P. 2014. Nonlinear forcing singular vector-type tendency errors of the Zebiak-Cane model and its effect on ENSO predictability [J].Climate Dyn. doi: 10.1007/s00382-014-2369-0.
龚道溢, 王绍武. 1999. 近百年ENSO对全球陆地及中国降水的影响 [J].科学通报, 44 (3): 315–320. Gong D Y, Wang S W. 1999. ENSO influence on global land and precipitation in China over the past century[J]. Chinese Science Bulletin (in Chinese), 44 (3): 315–320.
Jin E K, Kinter III J L, Wang B, et al. 2008. Current status of ENSO prediction skill in coupled ocean–atmosphere models [J]. Climate Dyn.,31 (6): 647–664.
Johnson B, Kumar V, Krishnamurti T N. 2013. Rainfall anomaly prediction using statistical downscaling in a multimodel superensemble over tropical South America [J]. Climate Dyn., 43 (7–8): 1731–1752, doi:10.1007/s00382-013-2001-8.
Kang I S, Yoo J H. 2006. Examination of multi-model ensemble seasonal prediction methods using a simple climate system [J]. Climate Dyn., 26(2–3): 285–294.
Ke Z J, Zhang P Q, Dong W J, et al. 2009. A new way to improve seasonal prediction by diagnosing and correcting the intermodel systematic errors[J]. Mon. Wea. Rev., 137 (6): 1898–1907.
Kharin V V, Zwiers F W. 2002. Climate predictions with multimodel ensembles [J]. J. Climate, 15 (7): 793–799.
Krishnamurti T N, Kishtawal C M, Timothy E L, et al. 1999. Improved weather and seasonal climate forecasts from multimodel superensemble[J]. Science, 285 (5433): 1548–1550.
Krishnamurti T N, Kishtawal C M, Shin D W, et al. 2000a. Improving tropical precipitation forecasts from a multianalysis superensemble [J]. J.Climate, 13 (23): 4217–4227.
Krishnamurti T N, Kishtawal C M, Zhang Z. 2000b. Multimodel ensemble forecasts for weather and seasonal climate [J]. J. Climate, 13 (23):4197–4216.
Krishnamurti T N, Chakraborty A, Krishnamurti R, et al. 2006. Seasonal prediction of sea surface temperature anomalies using a suite of 13 coupled atmosphere–ocean models [J]. J. Climate, 19 (23): 6069–6088.
Krishnamurti T N, Gnanaseelan C, Chakraborty A. 2007. Prediction of the diurnal change using a multimodel superensemble. Part I: Precipitation[J]. Mon. Wea. Rev., 135 (10): 3613–3632.
Krishnamurti T N, Mishra A K, Chakraborty A. 2009. Improving global model precipitation forecasts over India using downscaling and the FSU superensemble. Part I: 1–5 day forecasts [J]. Mon. Wea. Rev., 137 (9):2713–2735.
Krishnamurti T N, Kumar V. 2012. Improved seasonal precipitation forecasts for the Asian monsoon using 16 atmosphere–ocean coupled models. Part II: Anomaly [J]. J. Climate, 25 (1): 65–88.
Lorenz E N, Emanuel K A. 1998. Optimal sites for supplementary weather observations: Simulation with a small model [J]. J. Atmos. Sci., 55 (3):399–414.
Luo J J, Masson S, Behera S K, et al. 2008. Extended ENSO predictions using a fully coupled ocean–atmosphere model [J]. J. Climate, 21 (1):84–93.
Min Y M, Kryjov V N, Park C K. 2009. A Probabilistic multimodel ensemble approach to seasonal prediction [J]. Wea. Forecasting, 24 (3):812–828.
Mu M, Xu H, Duan W S. 2007. A kind of initial errors related to “spring predictability barrier” for El Niño events in Zebiak-Cane model [J].Geophys. Res. Lett., 34 (3), doi:10.1029/2006GL027412.
Mu M. 2013. Methods, current status, and prospect of targeted observation[J]. Science China Earth Sciences, 56 (12): 1997–2005.
Mu M, Yu Y S, Xu H, et al. 2013. Similarities between optimal precursors for ENSO events and optimally growing initial errors in El Niño predictions [J]. Theor. Appl. Climatol., 115 (3–4): 461–469, doi:10.1007/s00704-013-0909-x.
Peng P T, Kumar A, van den Dool H, et al. 2002. An analysis of multimodel ensemble predictions for seasonal climate anomalies [J]. J. Geophys. Res.,107 (D23): ACL 18-1–ACL 18-12, doi:10.1029/2002JD002712.
Sakai K, Kawamura R. 2009. Remote response of the East Asian winter monsoon to tropical forcing related to El Niño–Southern Oscillation [J]. J.Geophys Res., 114 (D6), doi:10.1029/2008JD010824.
Thompson P D. 1977. How to improve accuracy by combining independent forecasts [J]. Mon. Wea. Rev., 105 (2): 228–229.
Trenberth K E, Caron J M, Stepaniak D P, et al. 2002. Evolution of El Niño–Southern Oscillation and global atmospheric surface temperatures[J]. J. Geophys. Res., 107 (D8): AAC 5-1–AAC 5–17,doi:10.1029/2000JD000298.
van Oldenborgh G J, Doblas-Reyes F J, Wouters B, et al. 2012. Decadal prediction skill in a multi-model ensemble [J]. Climate Dyn., 38(7–8):1263–1280.
Wang B, Wu R G, Fu X H. 2000. Pacific–East Asian teleconnection: How does ENSO affect East Asian climate? [J]. J. Climate, 13 (9): 1517–1536.
杨学胜. 2001. 业务集合预报系统的现状及展望 [J]. 气象, 27 (6): 3–9.Yang X S. 2001. The new development and the outlook of the operational ensemble prediction system [J]. Meteorological Monthly (in Chinese), 27(6): 3–9.
Yatagai A, Krishnamurti T N, Kumar V, et al. 2014. Use of APHRODITE rain Gauge-Based precipitation and TRMM 3B43 products for improving Asian monsoon seasonal precipitation forecasts by the superensemble method [J]. J. Climate, 27 (3): 1062–1069.
Yun W T, Stefanova L, Mitra A K, et al. 2005. A multi-model superensemble algorithm for seasonal climate prediction using DEMETER forecasts [J].Tellus A, 57 (3): 280–289.
Zebiak S E, Cane M A. 1987. A model El Niño–Southern oscillation [J].Mon. Wea. Rev., 115: 2262–2278.
翟盘茂, 李晓燕, 任福民. 2003. 全球变化热门话题丛书——厄尔尼诺[M]. 北京: 气象出版社. Zhai P M, Li X Y, Ren F M. 2003. Global Change—El Niño (in Chinese) [M]. Beijing: China Meteorological Press.
Zhang J, Duan W S, Zhi X F. 2014. Investigation of the initial errors that cause the “spring predictability barrier” for El Niño events by using CMIP5 model outputs [J]. Sci. China Earth Sci., doi: 10.1007/s11430-014-4994-1.
张人禾, 周广庆, 巢纪平. 2003. ENSO动力学与预测 [J]. 大气科学, 27(4): 674–688. Zhang R H, Zhou G Q, Chao J P. 2003. On ENSO dynamics and its prediction [J]. Chinese Journal of Atmospheric Sciences(in Chinese), 27 (4): 674–688.
智协飞, 林春泽, 白永清, 等. 2009. 北半球中纬度地区地面气温的超级集合预报 [J]. 气象科学, 29 (5): 569–574. Zhi X F, Lin C Z, Bai Y Q,et al. 2009. Superensemble forecasts of the surface temperature in Northern Hemisphere middle latitudes [J]. Scientia Meteorologica Sinica(in Chinese), 29 (5): 569–574.
智协飞, 伍清, 白永清, 等. 2010. 基于IPCC-AR4模式资料的地面气温超级集合预测 [J]. 气象科学, 30 (5): 708–714. Zhi X F, Wu Q, Bai Y Q, et al. 2010. The multimodel superensemble prediction of the surface temperature using the IPCC AR4 scenario runs [J]. Scientia Meteorologica Sinica (in Chinese), 30 (5): 708–714.
Zhi X F, Qi H X, Bai Y Q, et al. 2012. A comparison of three kinds of multimodel ensemble forecast techniques based on the TIGGE data [J].Acta Meteor. Sinica, 26 (1): 41–51.
智协飞, 季晓东, 张璟, 等. 2013. 基于 TIGGE资料的地面气温和降水的多模式集成预报 [J]. 大气科学学报, 36 (3): 257–266. Zhi X F, Ji X D, Zhang J, et al. 2013. Multimodel ensemble forecasts of surface air temperature and precipitation using TIGGE datasets [J]. Trans. Atmos.Sci. (in Chinese), 36 (3): 257–266.
周菲凡, 张贺. 2014. 基于 CNOP方法的台风目标观测中三种敏感区确定方案的比较研究 [J]. 大气科学, 38 (2): 261–272, doi:10.3878/j.issn.1006-9895.2013.13129. Zhou F F, Zhang H. 2014. Study of the schemes based on CNOP method to identify sensitive areas for typhoon targeted observations [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 38 (2): 261–272, doi:10.3878/j.issn.1006-9895.2013.13129.
——以赣州市龙南县为例

