冬季北太平洋海气环流年代际异常的统计动力诊断
张东凌 吕庆平 张立凤
1 中国科学院大气物理研究所国际气候与环境科学中心, 北京100029
2 海军东海舰队司令部海洋水文气象中心,宁波315122
3 解放军理工大学气象海洋学院大气环流与短期气候预测实验室,南京211101
1 引言
随着海洋观测资料的长时间积累和数据同化产品的不断推出,20世纪90年代后,十年及以上年代际尺度的海洋气候变化已成为国际气候学研究中的热点问题。太平洋年代际振荡(Pacific Decadal Oscillation,PDO)是近年来揭示的北太平洋海表面温度(Sea Suface Temperature,SST)年代际时间尺度上的气候变率强信号(Mantua et al.,1997),对其基本特征国内外已有了许多研究(杨修群等,2004;吴德星等,2006;Alexander,2010;Liu,2012),其可直接造成太平洋及其周边地区大气环流的年代际变化(刘秦玉等,2010)。尽管如此,PDO仍不能完全解释东北太平洋中盐度、营养物、叶绿素及鱼储量等的年代际变化。为此 2008年Di Lorenzo(2008)对东北太平洋海域的海表面高度(Sea Surface Height,SSH)定义了一个新的气候模态——北太平洋环流振荡(North Pacific Gyre Oscillation,NPGO),它不仅能很好地反映风应力和海表面盐度距平的变化,而且与东北太平洋中生物变量的变化趋势有很好的相关性。因SST和SSH的变化趋势相关较高(Cummins et al., 2005),故在SST的年代际变化上也有NPGO模态。PDO和NPGO作为北太平洋SST异常(SSTA)的主要气候模态,已越来越受到人们的重视。
PDO和NPGO模态既是海气相互作用产生的自然现象,又受全球变暖的影响,同时也会显著地改变北太平洋各海洋要素的分布形态,并影响着大气环流形势和全球变暖趋势。研究认为北太平洋PDO 模态与大气中的阿留申低压(AL)(Trenberth and Hurrell, 1995)异常强迫有关(Chhak et al.,2009),而北太平洋NPGO模态则与大气中的北太平洋涛动(NPO)有关(Ceballos et al., 2009)。PDO模态和NPGO模态以及其相应的大气异常强迫,不但能从长时间序列的卫星观测资料中获得,而且可在海洋模式回报试验中得到证实(Qiu and Chen,2010),并能在IPCC AR4海气耦合模式中得到验证(Furtado et al., 2011)。
中纬度西风带急流和风暴轴的重要性是众所周知的 (Li et al., 2009)。西风急流造成的相应近地面的西风应力,其强迫会使海洋上层流动做出响应,并通过海气相互作用引起气候变化。虽然观测表明中纬度的海气相互作用较热带要小,对气候的影响也没有热带那样显著,但是有关这方面的工作依然引起气象和海洋学者的关注(朱艳锋等,2002;谭桂容等,2009)。风应力驱动上层海洋的理论早在上世纪 50年代就已提出,然而直到目前海洋对风应力响应的研究仍受到广泛的重视(Cabanes et al., 2006; Qiu and Chen, 2006; 张永垂和张立凤,2009;Zhang et al., 2010, 2011; 吕庆平等, 2013a)。
大洋流场与其他物理量,如海温等,受同一大洋运动方程组约束,故而流场与海温场之间有着紧密的联系,这样 SSTA的主要气候模态 PDO和NPGO必然会在大洋流场上有所反映,尽管目前尚未见到这方面的工作。上层大洋流场是受大气底层的风应力驱动的。这就表明上述SSTA的主要气候模态PDO和NPGO应与风应力关系密切,且风生流为海气相互作用的重要一环。为了揭示冬季北太平洋海气相互作用中大气与大洋环流年代际异常的机制,将大气风场和大洋流场看作一个整体进行统计动力诊断,即对其进行联合EOF分析是十分必要的。PDO和NPGO本来就是通过对SSTA的EOF分析来得到和定义的,其分别是该 EOF分析的第一、二模态。然而因大气风场和大洋流场都是向量,要其整体进行EOF分析则必须采用复EOF分析(张东凌等,2005;张东凌和何卷雄,2005;张东凌和曾庆存,2007)。
因复EOF分析编程有一定难度,故除我们先前所做的一些工作外(张东凌等,2005;张东凌和何卷雄,2005;张东凌和曾庆存,2007;卢姁和张东凌,2009a,2009b,2010),当前复EOF分析的有关工作尚很难见到,而对赤道外北太平洋大气风场和大洋流场进行联合复 EOF分析的有关工作也至今仍未发现。
本文将冬季赤道外北太平洋的大气与大洋环流异常看作一个整体,做了联合复EOF分析,对主要模态的时间系数做了小波分析;得到了其年代际变化的规律,并讨论了该联合复EOF分析的主要模态与SSTA的PDO、NPGO模态之间的关系;给出了气压场异常的AL、NPO模态在大气风场上的表现,以及SSTA的PDO、NPGO模态在大洋流场上的表现,并揭示了大气风场与大洋流场的耦合形式和各模态中海气相互作用的某些机理。
2 资料和方法
大气资料为 NCAR/NCEP提供的各年 2月份(以2月份作为冬季代表)1000、850、700、500、300、200、50 hPa 7个标准等压面上的月平均风场和气温场,资料年份取1950年到2001年,共计52年,网格距为2.5°×2.5°。
大洋资料为各年2月份(这里也以2月份为冬季代表)的Carton海洋上层洋流资料。该资料长度也从1950年到2001年,共计52年;其提供深度为 112.5、97.5、82.5、67.5、52.5、37.5、22.5、7.5 m共8层上的逐月平均洋流,该资料为高斯网格,在本文研究范围内的分辨率约为1°×1°;而该研究范围为(30°N~60°N,120°E~110°W),包括赤道外北太平洋海域和其周边的陆地。
将大气资料插值到海洋资料(约1°×1°)的网格点上;而在上述研究范围的陆地部分,设海洋的流动为0。这样处理后各年2月份大气月平均风场和大洋月平均流场两者在垂直方向上总共有 15层(大洋8层,大气7层)。因洋流速度与大气风速相差2个量级,故必须对上述月平均风场和流场做如下处理:
将各层月平均风场和流场的速度乘以相应层次月平均密度的开方;这样就使两者的量级接近。为方便,以下仍分别称之为月平均风场和流场,但这里该风场或流场的内积是单位体积的动能。各层大气的月平均密度可通过状态方程由月平均温度来求得(该温度也来自 NCAR/NCEP资料),而大洋密度则取水的标准密度(因海水密度变化很小)。
对以上处理过的各年2月份各层的月平均风场和流场分别求 52年平均的气候场,并将该月平均风场和流场分别减去此气候场,便可分别得到相应的风场异常和流场异常,而这两者均是一个二维向量。本文将该风场异常和流场异常看作一个整体,在上述 15层上来做联合复经验正交函数(为行文方便,以下简称为CEOF)分析。
对二维向量场进行经验正交函数分解,则必须要用复EOF分析,这是因为一个二维向量的两个分量不是真正意义上的标量,而用一个复数则可以表示一个二维向量。在采用复EOF分析时,其时间系数是复数,仅当其辐角大致分布在两个状态附近时,因这两个状态可用“+”、“-”两个符号来表示,此时才能将该二维向量的两个分量看作两个标量来进行实 EOF分析。实际操作表明,通常复EOF得到的第一模态辐角均分布在两个状态附近,而第二、三及以后模态则有可能辐角分布在更多状态,且模态越高这种可能性就越大;对于后者的情况就只能用复EOF分析而不能用实EOF分析了,若用实 EOF分析则会得到错误的结果。在能用实EOF分析的情况下(如第一模态),由于变量数增加了一倍(由一个向量变成两个标量),其模态的方差贡献就较小,也不易通过检验。实EOF分析虽然编程比复EOF分析方便(前者有现成程序可用),但后者一旦编好程序,运算起来也很方便;故一般对二维向量(如大气风场等),必须采用复EOF分析,特别在不知其模态辐角分布的情况下。
该CEOF分析的第一、二模态的方差贡献分别为28.2%和13.6%,并通过了North检验。受篇幅限制,本文主要讨论大洋中深度为7.5、22.5、112.5 m和大气中850、500、200 hPa这6层的特征,它们可作为大洋表层、近表层、次表层和大气对流层低、中、高层的代表。下面对该CEOF第一、二模态的空间场和时间系数进行讨论。
3 CEOF的第一模态
3.1 空间场
图1a–c给出了200、500、和850 hPa 大气环流异常CEOF分析的第一模态的空间场。由图可见:各层在北太平洋中部,均存在一个气旋性环流异常中心,气旋环流几乎控制了整个北太平洋,其属大气的行星尺度系统;在30°N~35°N的北太平洋中部,均有明显的偏西风异常,而高纬则均有偏东风异常;考虑到行星尺度风场与气压场之间应满足准地转关系后,则该第一模态类似于AL模态正位相的空间结构,不妨称其为 AL模态的风场模。AL是深厚的系统,从850 hPa直到200 hPa其风场均表现为气旋环流;在此第一模态的偏差流场分布从对流层低层到高层也大体相似;但注意到各层该模态的气旋性环流异常中心的位置则并不重合,其从低层到高层有明显的向西偏斜(参见图1),而这正反映了大气的斜压性。
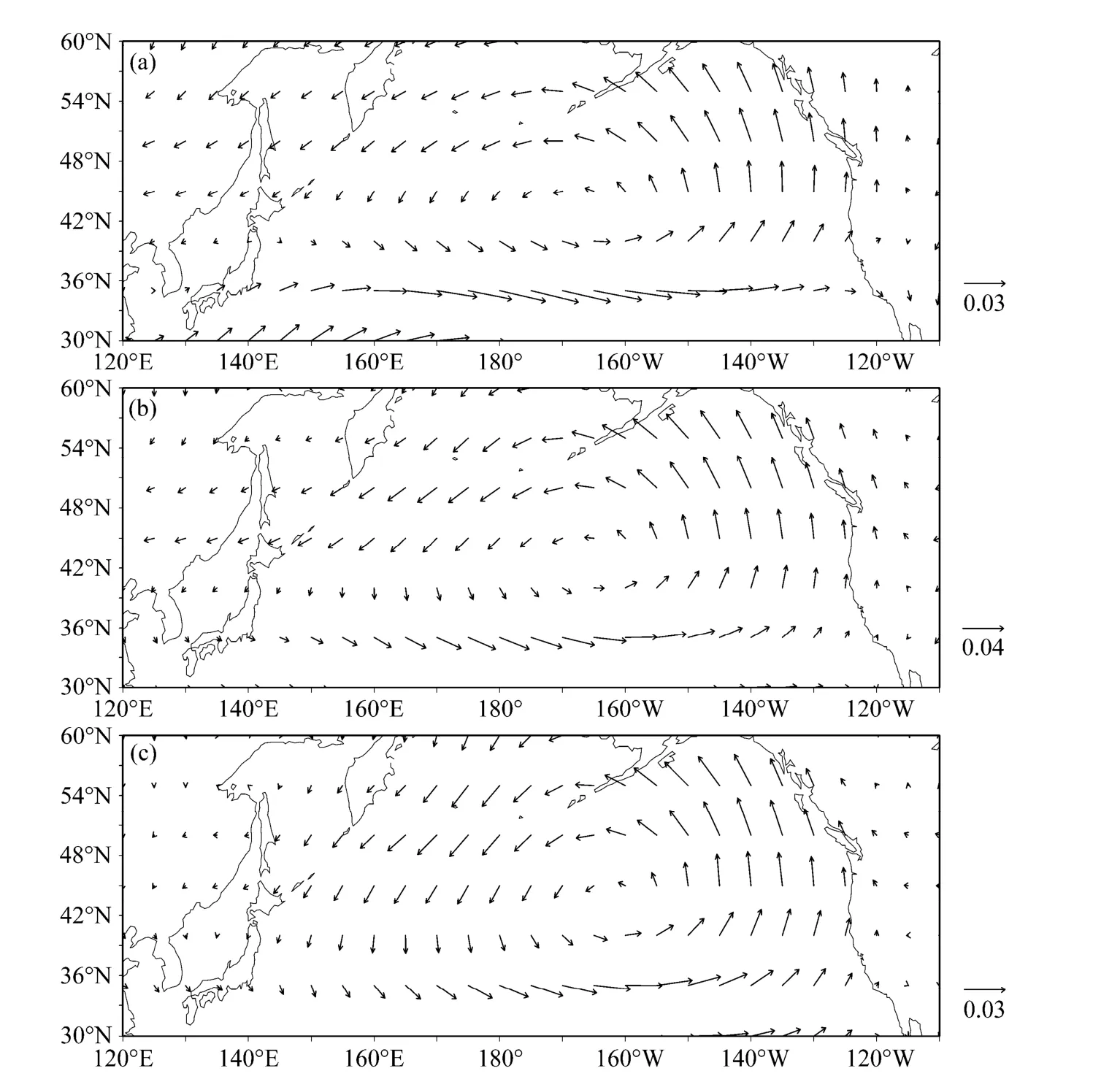
图1 大气环流异常复经验正交函数(CEOF)分析的第一模态的空间场:(a)200 hPa;(b)500 hPa;(c)850 hPaFig. 1 Atmospheric circulation anomalies of the first Complex Empirical Orthogonal Function (CEOF) mode: (a) 200 hPa; (b) 500 hPa; (c) 850 hPa
图2a–c给出了7.5、22.5、112.5 m大洋环流异常CEOF分析的第一模态的空间场。由图可见:在7.5 m层上,大洋环流异常在北太平洋中东部表现为辐散场,并略带气旋式旋转;在接近大洋西海岸的日本本州岛以东、以南海域则有较强的流场异常。在22.5、112.5 m,北太平洋中东部的辐散场大体消失,变为一个北太平洋海盆尺度气旋式旋转的大洋环流,尤其在112.5 m这表现得更为明显;而在日本本州岛以东、以南海域的流场异常则较强,其表现为一个长轴呈北东北—南西南向的椭圆形气旋涡旋,中心位于(34°N,143°E)。在22.5 m以下至 112.5 m,大洋环流异常的差异较小,这表明该范围的海洋具有正压性。
3.2 时间系数
因这里将大气环流异常和上层大洋环流异常看作一个整体进行CEOF分析,故各层大气环流异常和大洋环流异常具有相同的时间系数,这就有利于讨论两者的耦合关系。因这里进行的是CEOF分析,故时间系数由一个复数来表示。
从时间系数的辐角分布可见(图3a):其辐角分别集中于0°或±180°附近,这表示耦合的风和流的异常只有两个状态 A、B,其对应的流型分别与该CEOF第一模态空间场相似或相反。
从第一模态时间系数的模(图3b)可见,其值每年各不相同,为此可求其 52年平均值。各年以该平均值为界,可将其划分为两个态:大于等于该平均值的称为强模态,用S表示;小于该平均值的则称为弱模态,用 W 表示;而各年模的数值则决定了其异常的强弱程度,数值越大则其异常越强。
经以上处理后则能得到 4种配置组合:AS、BS、AW、BW;其中AS和BS是两个强异常的状态。对AS态,大气和大洋环流异常流型分布分别表现为与CEOF第一模态空间结构相同的态势,而对BS态,大气和大洋环流异常流型分布则与CEOF第一模态空间结构相反,对这两者异常的强度则均较强。

图2 大洋环流异常CEOF分析的第一模态的空间场:(a)7.5 m;(b)22.5 m;(c)112.5 mFig. 2 Oceanic circulation anomalies of the first CEOF mode at the depths of (a) 7.5 m, (b) 22.5 m, and (c) 112.5 m
因辐角值集中在0°和±180°附近,可对时间系数的辐角和模作如下处理:将各年辐角的余弦乘以相应的模则可得一新值,而这些新值可重新构成一个实时间系数序列。因实时间系数操作简单,且其分析结果与复时间系数一致,故以下对该实时间系数序列进行讨论。
因本文主要关心北太平洋年代际异常中大气和大洋环流的耦合和相互作用问题,为了排除年际变化(主要是ENSO)的干扰,在此对CEOF第一模态的实时间系数做了4年高斯滤波,滤波后的实时间系数序列如图4a所示。由该图可见,该序列仍存在年际变化以及明显的年代际变化。为揭示其变化规律,在此作了小波分析。图5a给出了该序列的小波全谱。由该图可见,在年际变化上,即使经过了4年的高斯滤波,3~8年的周期仍明显,这应该反映了ENSO的影响,并表明该影响对第一模态是显著的;在年代际变化上,则以21~22年的周期最显著。从该序列的小波功率谱可见(图略),明显的21~22年的年代际变化贯穿了整个52年的始终。
该序列的小波全谱与冬季北太平洋SSTA EOF分析第一模态(PDO模态)时间系数的小波全谱(路凯程等,2011),均具有准22年的年代际变化。本文还计算了该序列与 PDO指数序列的相关系数,其值为0.57,两者具有正相关性。
4 CEOF的第二模态
4.1 空间场
图6a–c给出了200、500和850 hPa 大气环流异常CEOF分析的第二模态的空间场。由该图可见,各层大气环流异常的分布态势也相近,考虑到风场与气压场的准地转关系后,该分布类似于 NPO模态的负位相;即在北太平洋高纬的170°E附近,其环流异常为反气旋曲率,在(35°N,155°W)附近,环流异常则表现为气旋性曲率,而在 40°N的东太平洋和在40°N~50°N的北太平洋中西部,则有偏东风异常。这里不妨将其称为NPO模态的风场模。注意到在30°N至55°N从850 hPa至200 hPa的北太平洋均为西风带,故该风场模反映了上述西风带的异常。与第一模态类似,在此第二模态流场偏差中,各层的反气旋性环流中心和气旋性曲率从低层到高层都有明显的向西偏斜,这也体现了大气的斜压性。

图3 环流异常CEOF分析第一模态时间系数的(a)辐角和(b)模Fig. 3 The (a) argument and (b) modulus of the first time series of circulation anomalies of CEOF
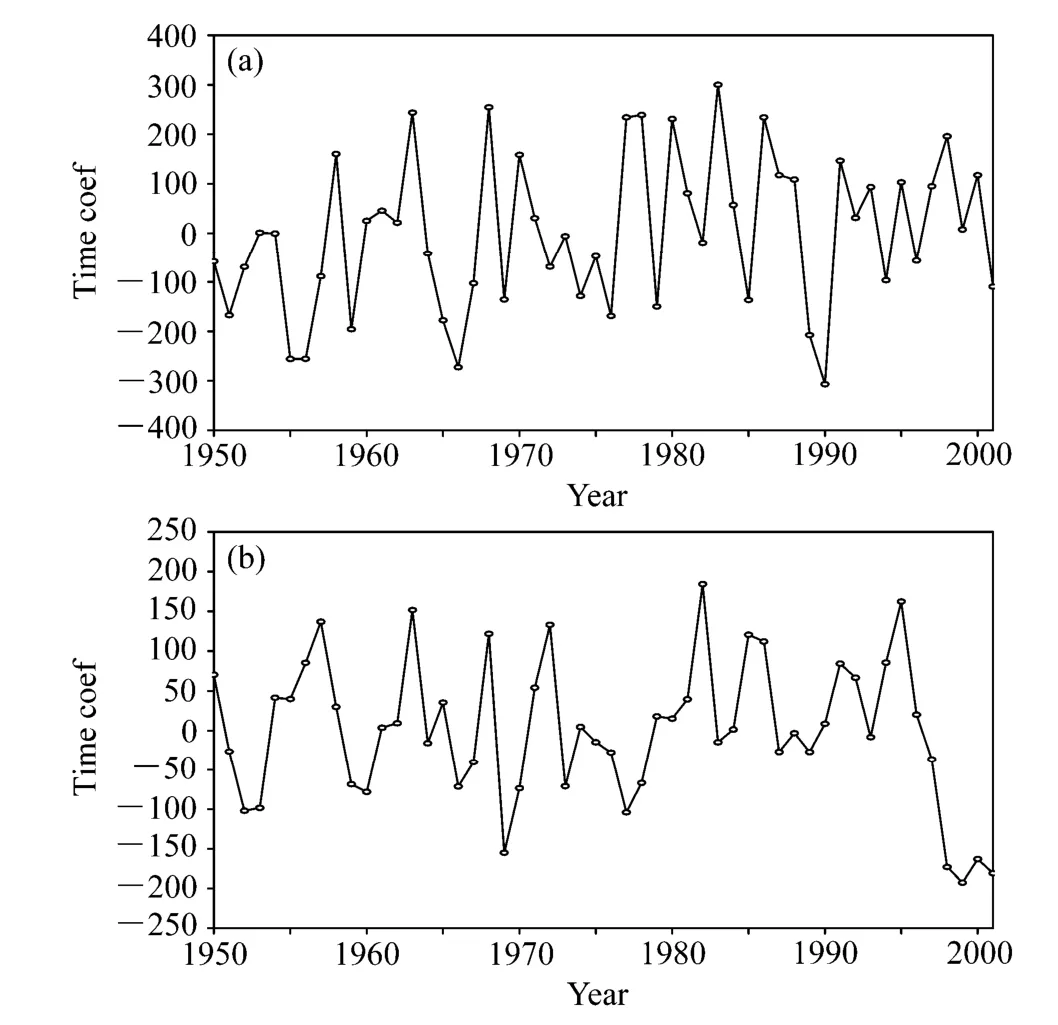
图4 环流异常CEOF分析(a)第一、(b)二模态滤波后实时间系数的折线图Fig. 4 The filtered (a) first and (b) second time series of circulation anomalies of CEOF
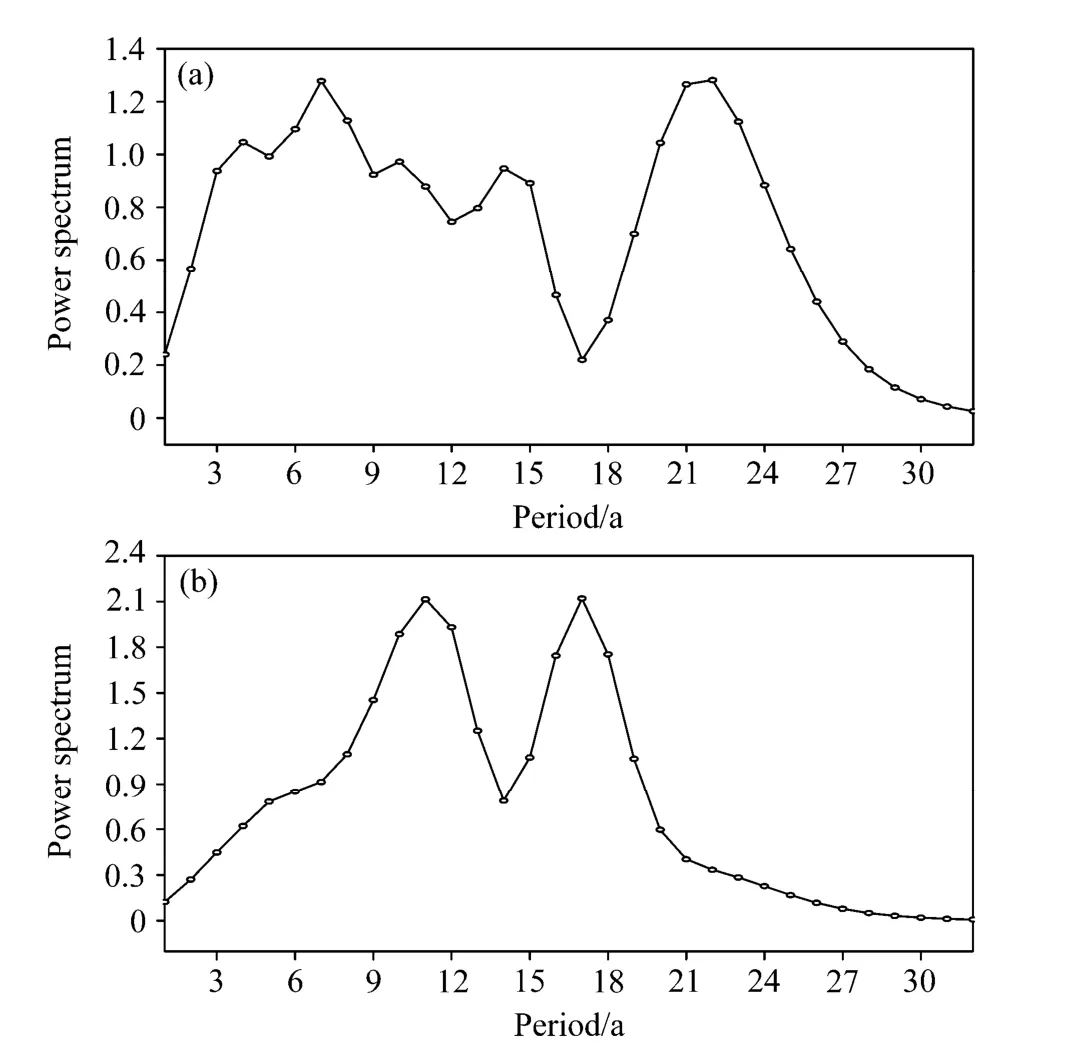
图5 环流异常CEOF分析(a)第一、(b)二模态滤波后实时间系数的小波全谱Fig. 5 The wavelet spectrum of the filtered (a) first and (b) second time series of circulation anomalies of CEOF
图7 a–c给出了7.5、22.5、112.5 m大洋环流异常CEOF分析的第二模态的空间场。由该图可见,在7.5 m层大洋环流异常在中高纬度为反气旋性环流,中心在(57°N,170°W)附近;中纬度为气旋性环流,中心在(35°N,155°W)附近;两者交界的 40°N附近的北太平洋中部则为西向流;以上系统均具有北太平洋海盆尺度;在日本本州岛以东海域则有范围不大的气旋性曲率流动。在包括22.5 m层至112.5 m的海洋上层,大洋环流异常的差异也不大,在此上述的北太平洋海盆尺度大洋环流系统的强度明显减弱;西海岸附近的流场异常相对突出。日本本州岛以东气旋性曲率流动则已成为气旋涡旋,中心位于(37°N,150°E)附近;在堪察加半岛东南方海域则有反气旋涡旋,中心位于(48°N,162°E)附近;这两个涡旋的中心连线呈东北—西南走向,且两个涡旋分别位于CEOF分析第二模态的西太平洋强东风异常(参见图7b,c)的两侧,构成一对涡旋偶。
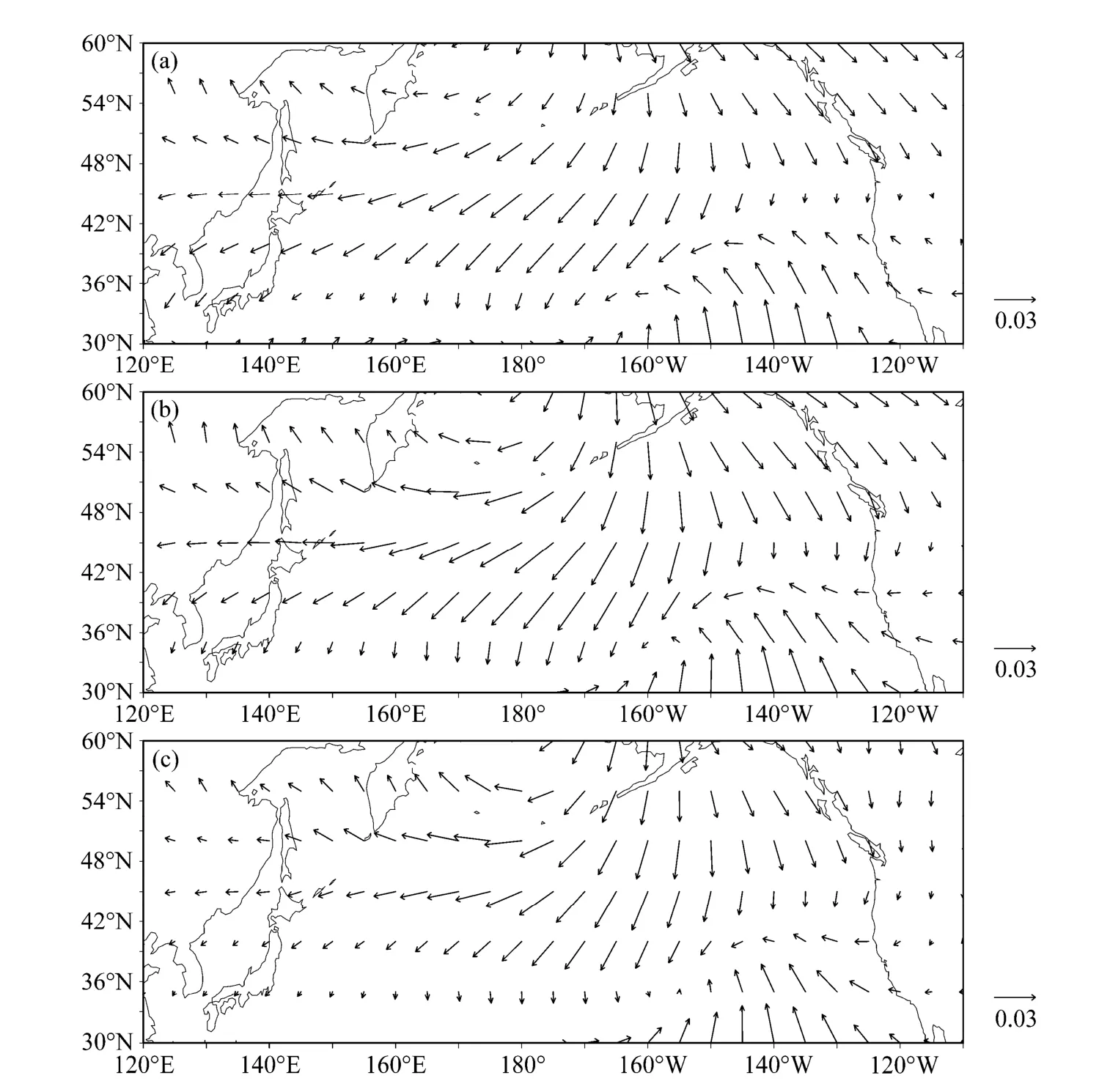
图6 大气环流异常复经验正交函数(CEOF)分析的第二模态的空间场: (a) 200 hPa; (b) 500 hPa; (c) 850 hPaFig. 6 Atmospheric circulation anomalies of the second CEOF mode: (a) 200 hPa; (b) 500 hPa; (c) 850 hPa
4.2 时间系数
第二模态时间系数的辐角也分别集中于 0°或±180°附近(图8a),这表示耦合的风和流的异常也只有两个状态 A、B,不过此时辐角在这两个状态的离散度要较第一模态大。图8b给出了时间系数的模。仿照第一模态的做法,对此模也能划分为强模态S和弱模态W。这样也能得到4种配置态:AS、BS、AW、BW;AS、BS态的意义与 CEOF第一模态的相同,不再赘述。
仿照第一模态的做法,对第二模态,亦可得到综合反映辐角和模随时间演变的实时间系数序列。在此也对该实时间系数做了 4年高斯滤波。图4b给出了滤波后第二模态实时间系数序列的折线图。由该图可见,CEOF第二模态该序列也具有年际变化和明显的年代际变化。
为揭示该序列的变化规律,这里做了小波分析。图5b给出了该序列的小波全谱。由该图可见,该序列具有十分明显的11~12年和准17年的年代际变化,两者呈并列的双峰分布,而从年际变化看,ENSO的影响则较第一模态要小。本文还计算了该序列的小波功率谱(图略)。该功率谱图上有明显 11~12年的年代际变化,主要出现在1976/1977年气候突变后,并在1988/1989年气候突变后变得更加明显。从第二模态时间系数模的序列可见(参见图8b),在 1976/1977年气候突变后其变化态势与之前有明显不同,在该突变前其模值呈振荡减小趋势;在该突变后至1988/1989年气候突变前,其模值振幅加大;而在1988/1989年气候突变后,其模值则呈振荡增大趋势;这与NPGO指数的标准化时间序列的变化相一致(该序列的下载地址为:http://www.ocean3d.org/npgo)。在该小波功率谱图上,还可见 17年的年代际变化基本上表现在整个52年中,并在1976/1977年的气候突变后有所加强。
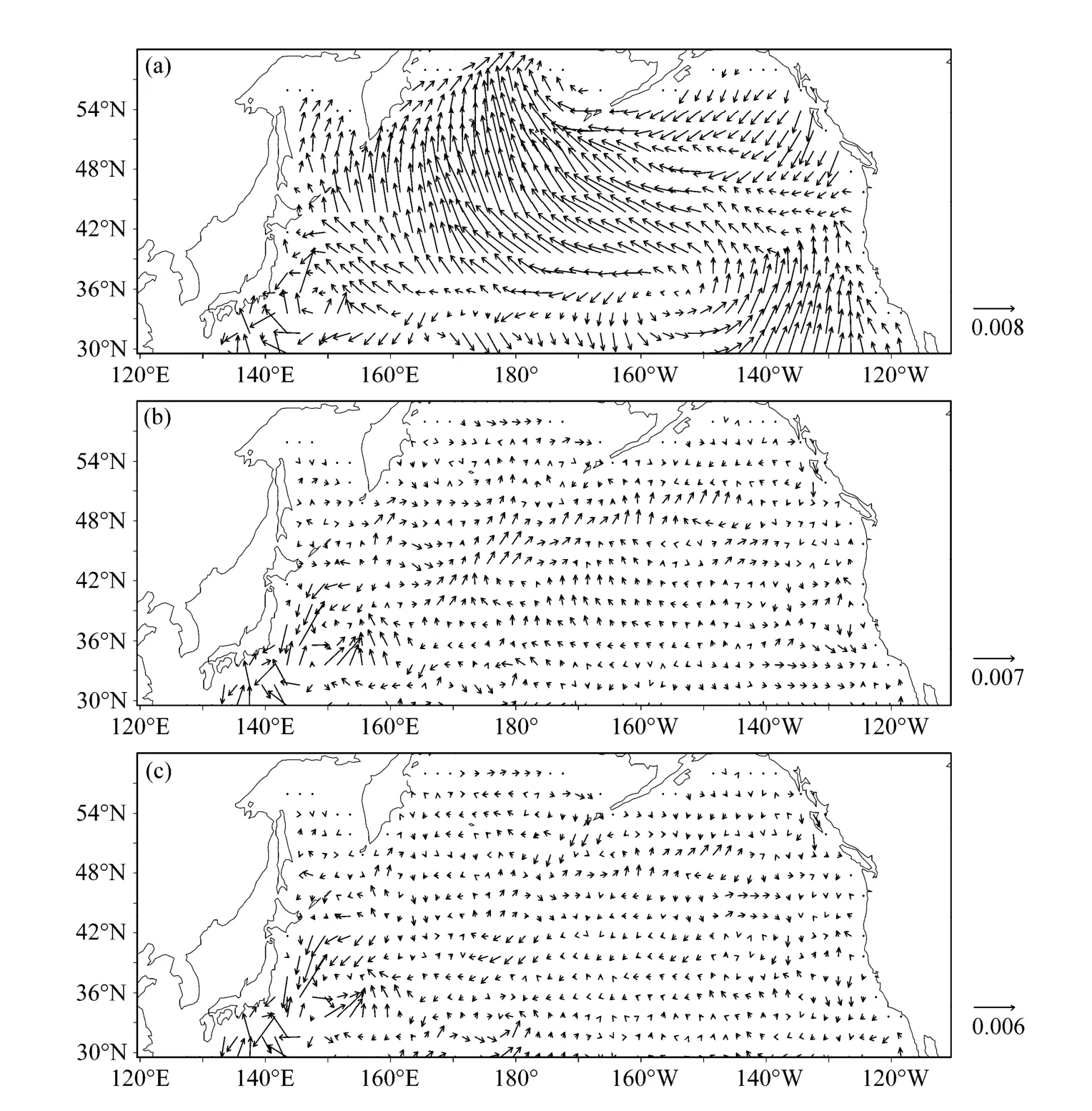
图7 大洋环流异常CEOF分析的第二模态的空间场: (a) 7.5 m; (b) 22.5 m; (c) 112.5 mFig. 7 Oceanic circulation anomalies of the second CEOF mode at the depths of (a) 7.5 m, (b) 22.5 m, and (c) 112.5 m
CEOF第二模态11~12年的年代际变化周期与冬季北太平洋SSTA EOF分析第二模态(NPGO模态)12~13年的周期相同,请参见张立凤和吕庆平①张立凤, 吕庆平. 2011. 冬季北太平洋NPGO模态与大气NPO模态的关系. 第二十八届中国气象学会年会中的图3,只是前者还存在较明显的准17年周期;在该文献图3上,还给出了冬季海平面气压异常(SLPA)EOF第二模态时间序列的小波全谱,并可见其除有与上相同的最显著的 13~14年的周期外,还有明显的 17~18年的周期。由此可知本文CEOF第二模态准17年的周期应来源于SLPA的影响。本文还计算了该序列与NPGO指数序列的相关系数,其值为-0.59,这表明两者具有负相关性。
5 有关海气耦合环流异常的讨论
5.1 海气耦合环流异常与SSTA的关系
为了揭示以上CEOF分析第一、二模态,即海气耦合环流异常第一、二模态与SSTA的第一模态(经典PDO模态)和第二模态(经典NPGO模态)的关系,利用SSTA 与CEOF第一、二模态未作滤波的实时间系数求回归,回归系数场见图9。这里为了与经典PDO模态和NPGO模态的空间结构作对比分析,则取研究范围为(24°N~62°N,110°E~110°W)。
根据PDO和NPGO不同的空间结构,可区分为冷、暖位相,或称为冷、暖“事件”。经典 PDO暖位相时,北太平洋中部为冷异常,沿北美西岸为暖异常,相应的 PDO指数则为正值;反之,则为经典PDO 冷位相,该指数则为负值。经典NPGO暖位相时,北太平洋南部为暖异常,北部为冷异常,南北向偶极子温度异常呈北冷南暖态势。相应的NPGO指数为正值;反之则为经典NPGO冷位相,则该指数为负值。
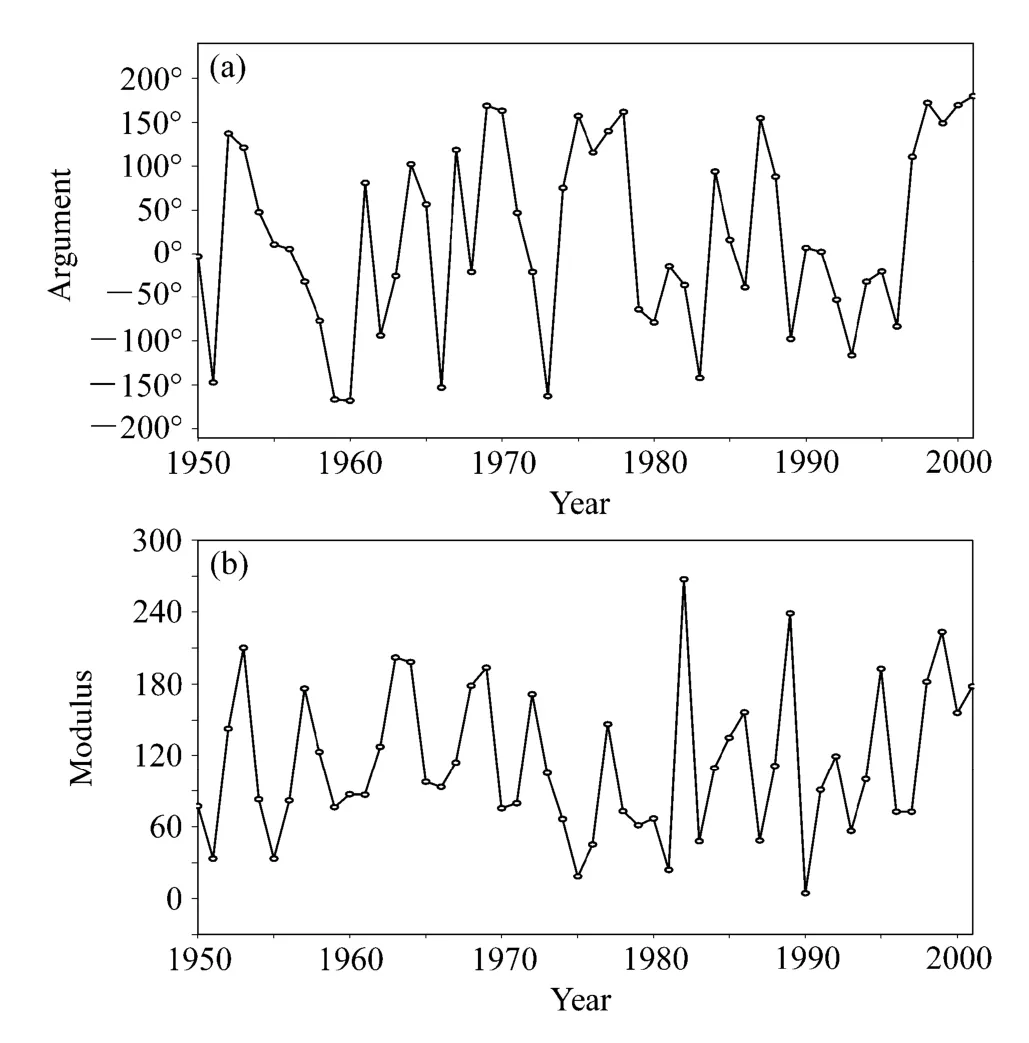
图8 环流异常CEOF分析第二模态时间系数的(a)辐角和(b)模Fig. 8 The (a) argument and (b) modulus of the second time series of circulation anomalies of CEOF
由图9a可见,由第一模态得到的回归场分布:在北太平洋中部存在一个椭圆形的负值区,负值中心位于(35°N,158°W)附近,北美西岸为正值区。这样的空间分布类似于经典 PDO模态的暖位相。由图9b可见,由第二模态得到的回归场分布:在北太平洋中高纬,从 150°E附近向东一直延伸至130°W则为正值带,其上有正大值中心;在其以南的副热带海域,从 140°E附近向东一直延伸至150°W附近均为负值带,其上则有负大值中心;两者构成北正南负的双带系统,其上的大值中心则呈偶极子分布,而两者的零线则交汇在35°N 附近。这样的空间分布类似于经典NPGO模态的冷位相。
为了更客观地表现这种相似性,分别计算了经典PDO、NPGO模态的空间场与以上第一、二模态回归场之间的场相关系数,其值分别高达 0.86和-0.88。由此可见,北太平洋大气大洋耦合环流CEOF第一、二模态实时间系数的回归场,其与经典SSTA的PDO和NPGO模态的空间分布非常相似。从该CEOF分析的第一、二模态的时间系数序列的年代际变化看,其最显著的年代际变化周期分别为准22年和11~12年,这与PDO模态和NPGO模态的年代际变化相同。以上表明,北太平洋大气大洋耦合环流的第一、二模态分别与 PDO模态和NPGO模态相对应,也即其是PDO模态和NPGO模态在该耦合环流上的反映。
5.2 影响PDO及NPGO的途径
海洋近表层的垂直运动异常与海温动力异常有密切关系,当该层某处垂直运动为正,即有上升流时,则会造成该处的动力降温;反之亦然。由本文CEOF分析得到的模态流场异常可直接计算其各层的散度场异常,对该散度场异常在垂直方向积分则可算得相应的垂直速度异常;在此取海气界面处的海洋垂直运动w≈0;这样w>0(w<0)则对应于上升(下沉)运动异常(张东凌和何卷雄,2005);而由近表层的垂直速度异常则可方便地决定 SSTA的动力变化。
图10a给出了由CEOF分析的第一模态22.5 m层上流场异常计算得到的垂直运动场异常。由该图可见,除高纬度的北太平洋西北部和东北部外,几乎整个北太平洋海盆均为上升运动区,其中北太平洋中部上升运动最强,这样会造成此处有明显的动力降温;这种降温会造成该处上层海温异常呈现偏低态势,形成低海温中心。而经典 PDO模态的空间结构则与该第一模态近表层垂直运动异常的态势相类似。这里海温动力变化的空间尺度为北太平洋海盆尺度,这说明由第一模态流场异常得到的海盆尺度垂直运动异常,其所造成海盆尺度海温异常的动力变化是产生PDO模态的重要原因。
图10b给出了由CEOF分析的第二模态近表层流场异常计算得到的垂直运动异常。由该图可见,在155°E至160°W以东的北太平洋22.5 m层上,约以 45°N为界,其北部为下沉运动,南部为上升运动,并也构成双带系统,且其上的下沉、上升大值中心在中太平洋也大体呈现偶极子形态。这样的海盆尺度垂直运动在海盆尺度海温动力变化上相应造成北高南低的双带系统及其上的偶极子(这是第二模态实时间系数大于0的情况,当小于0时,则垂直运动反向)。吕庆平等(2013b)给出了海洋上层海温联合EOF分析的结果,从其第二模态空间
场上从近表层到次表层海盆尺度的海温异常分布可见,在北太平洋都表现为北低南高的双带系统并有偶极子存在。因近表层到次表层离海面有一定距离,故可认为辐射对该处的海温异常影响不太大,故此海温异常基本代表了海温的动力异常。本文22.5 m层上垂直运动异常引起的海温动力异常的空间分布则与该文献的结果相似,只是两者位相配置相反(注意,因两者时间系数的符号也大致相反,故本质相同)。这也表明,由第二模态流场异常得到的海盆尺度垂直运动异常,其所造成海盆尺度海温异常的动力变化是产生NPGO模态的重要原因。
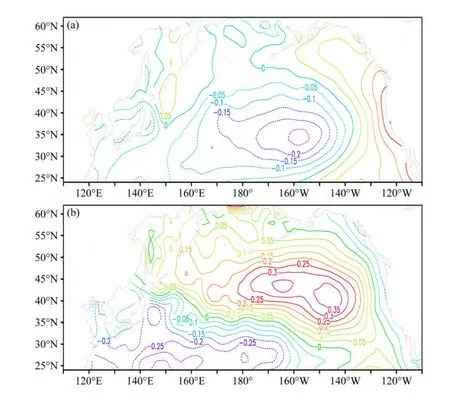
图9 SSTA与CEOF(a)第一、(b)第二模态实时间系数的回归系数场Fig. 9 Regression coefficients of SST anomalies and the (a) first and (b) second real time series of CEOF
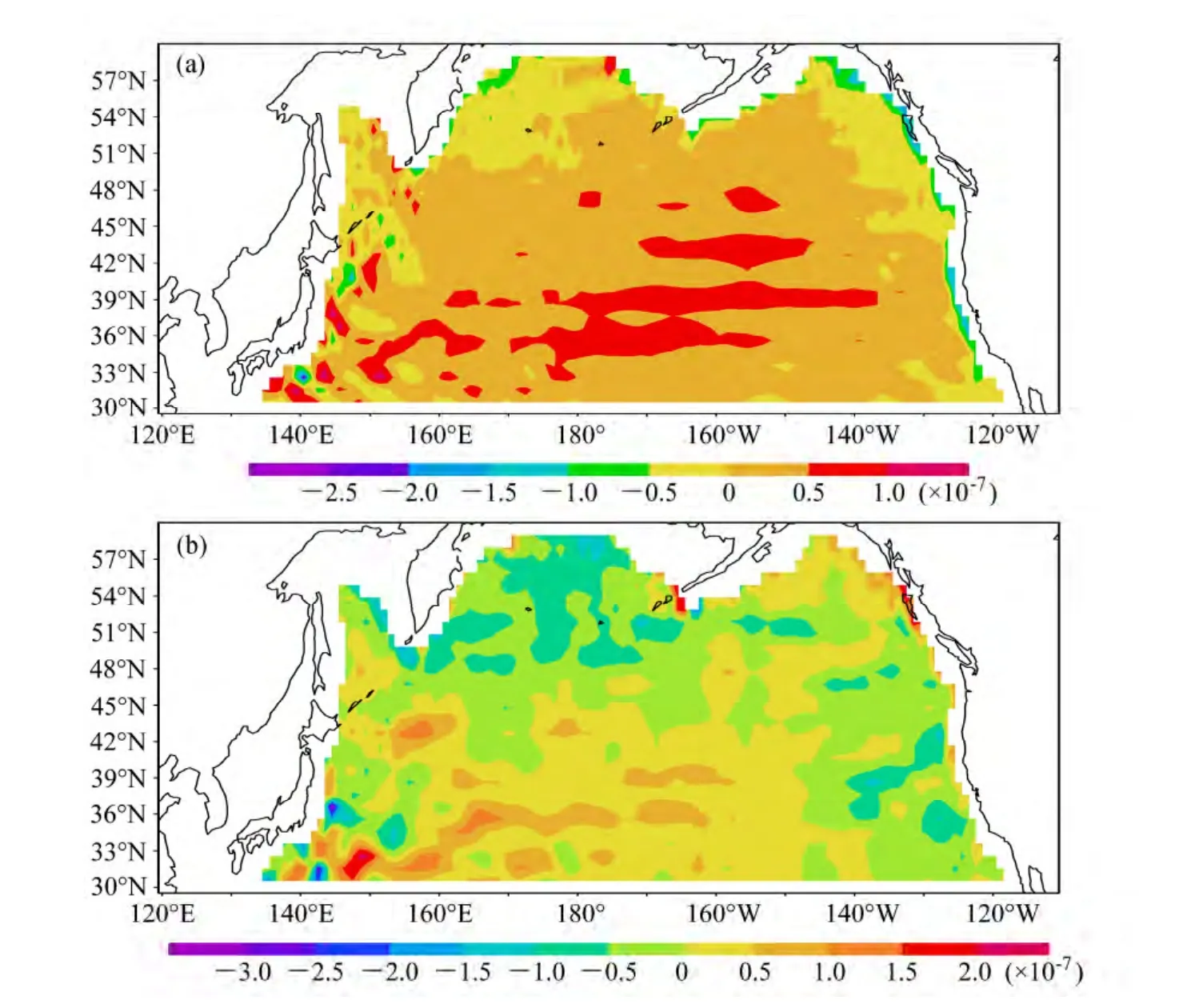
图10 CEOF(a)第一、(b)第二模态22.5 m层的垂直运动场 (单位:×10-7 m)Fig. 10 The (a) first and (b) second CEOF modes for vertical velocity at the depth of 22.5 m (units: ×10-7 m)
张铭等①张铭, 吕庆平, 路凯程. 2013. PDO流场模的解析求解I——经向风强迫的情况. 第三十届中国气象学会年会(Section 6)、吕庆平等②吕庆平, 路凯程, 张铭. 2013. PDO流场模的解析求解II——纬向风强迫和经纬向风共同强迫的情况. 第三十届中国气象学会年会(Section 6)和吕庆平和张铭(2012)利用一个西海岸线呈南北向、在中纬度β通道中的正压准平衡线性化半无界理想海洋模型,在分别考虑了类似本文第一、二模态风场异常的强迫后,求得了此理想海洋流场异常的解析解。发现这些解都有类似本文第一、二模态流场的海盆尺度的大洋环流异常。这就进一步表明,本文第一、二模态的流场异常确实是因本文第一、二模态风场异常强迫所致。
以上结果说明,在冬季北太平洋大气大洋耦合环流异常的第一、二模态中,大气风场与大洋流场的耦合情况在这两模态中是各不相同的,从而造成了流场异常及海温动力变化的不同,产生了 PDO和NPGO模态;而大气环流异常、大洋环流异常和上层海温的动力异常三者具有紧密的联系,并与SSTA的PDO模态和NPGO模态关系密切;这里大洋环流异常起着关键的中介作用。因海洋上层的流动为风生流,大气的风场(风应力)异常造成了大洋上层海盆尺度的流场异常,后者又造成了海洋海盆尺度垂直运动的异常,而这又会造成上层海温海盆尺度的动力变化,从而造成了海盆尺度的海温异常,而该海温异常则与PDO模态与NPGO模态相一致;这样本文就给出了风应力异常导致海温PDO与NPGO模态的中间环节和机制。为此不妨分别称CEOF中第一、二模态的大洋环流异常为 PDO和NPGO模态的流场模。
5.3 强异常区风场与流场耦合情况解释
日本本州岛以南的黑潮和黑潮延伸体的所在是北太平洋流场异常十分明显的海域,以下简称该海域为强异常区,其大致位于(30°~43°N,134.5°~154.5°E)范围内(路凯程等,2011)。从本文CEOF分析结果看,在强异常区的近表层至次表层(22.5~112.5 m)中,第一、二模态的流场异常也十分明显(参见图2和图7)。在该区及其附近,第一、二模态风场与流场的耦合情况是各不相同的,下面对此进行说明。
对第一模态而言,在强异常区及其附近,即在大洋的西海岸线附近,大气强迫风场异常大致与西海岸线平行;而在此处近表层至次表层的大洋环流异常则表现为一个长轴平行于此西海岸线的椭圆形环流。在张铭等①和吕庆平等②求得的上小节中所述的理想海洋对风场异常响应的解析解上,发现在纬向风和经向风异常的共同强迫下,在该海洋西边界外的海域,流场异常有气旋性涡旋出现;这与本文第一模态流场异常空间场在此处的分布相一致。
对第二模态而言,在强异常区及其附近,大气强迫风场大致为平行于纬圈的西风急流异常;而在该处的近表层至次表层,大洋环流异常则表现为:在该急流异常的南北两侧分别有气旋和反气旋涡旋,前者中心在(37°N,150°E)而后者中心在(48°N,162°E),两者构成了涡旋偶。在吕庆平和张铭(2012)中求得了上述理想海洋对西风急流强迫响应的解析解,并可知在理想海洋西海岸线外的海域,流场异常对风场异常的响应表现为涡旋偶的形态,这与本文第二模态流场异常空间场在此处的分布相一致。
上面已指出,本文CEOF分析得到的第一、二模态最明显的流场异常均出现在上述强异常区中,其表现为涡旋形式,且该异常在近表层至次表层大体不变。由图9a、b中可见,在该涡旋处,存在小范围的强垂直运动中心,这会造成该处海温的强动力异常。路凯程等(2011)、吕庆平等(2013b)分别给出了上层海温异常EOF分析第一、二模态的空间场,发现该处在近表层至次表层确实有很强的海温异常,这就证实了本小节的结果。
6 结语
本文对冬季北太平洋大气和大洋环流做了联合复EOF分析和小波分析,并分别讨论了第一、二模态的年代际变化及其与 PDO、NPGO模态的关系,得到了以下主要结论:
(1)对联合复EOF第一(二)模态实时间系数的分析发现,其与PDO(NPGO)指数有明显相关,其相关系数达0.57(-0.59);小波分析表明,第一(二)模态有显著的21~22(11~12)年的年代际变化,这与SSTA的PDO(NPGO)模态的年代际变化相同。
(2)联合复EOF第一(二)模态实时间系数与北太平洋SSTA空间场的回归分析表明,回归系数场的空间分布与经典PDO(NPGO)的空间场十分接近,两者的场相关系数高达0.86(-0.88)。
(3)在联合复EOF第一(二)模态的空间结构中,大气环流异常分别类似于地面气压场异常的AL(NPO)模态,可称其为AL(NPO)模态的风场模;而大洋环流异常则分别相应于SSTA的PDO(NPGO)模态,可称其为 PDO(NPGO)模态的流场模。
(4)从联合复EOF第一(二)模态近表层流场异常得到的海盆尺度垂直运动异常的空间分布与PDO(NPGO)的相似;这表明大气风场异常强迫出了海洋上层海盆尺度的大洋环流异常,后者造成的垂直运动导致了海盆尺度海温的动力变化,而该变化则是形成PDO(NPGO)的重要原因,在此该大洋环流异常扮演了中介角色。
最后要说明的是,本文的工作是诊断分析,故对海气相互作用年代际变化的具体机理揭示得尚不够充分,特别是在海洋对大气的影响方面。这方面的工作有待利用分析大洋模式和海气耦合模式的数值实验结果来解决,这也是我们下一步的研究方向。
(References)
Alexander M. 2010. Extratropical air–sea interaction, SST variability and the Pacific decadal oscillation [M]// Sun D, Bryan F, Eds. Climate Dynamics: Why Does Climate Vary?. Washington D C: Am. Geophys.Uninon, 123–148.
Cabanes C, Huck T, de Verdière A C. 2006. Contributions of wind forcing and surface heating to interannual sea level variations in the Atlantic Ocean [J]. J. Phys. Oceanogr., 36: 1739–1750.
Ceballos L I, Di Lorenzo E, Hoyos C D. 2009. North Pacific Gyre Oscillation synchronizes climate fluctuations in the eastern and western boundary systems [J]. J. Climate, 22 (19): 5163–5174.
Chhak K C, Di Lorenzo E, Schneider N, et al. 2009. Forcing of low-frequency ocean variability in the Northeast Pacific [J]. J. Climate,22 (5): 1255–1276.
Cummins P F, Lagerloef G S E, Mitchum G. 2005. A regional index of northeast Pacific variability based on satellite altimeter data [J]. Geophys.Res. Lett., 32: L17607, doi:10.1029/2005GL023642.
Di Lorenzo E, Schneider N, Cobb K M, et al. 2008. North Pacific Gyre Oscillation links ocean climate and ecosystem change [J]. Geophys. Res.Lett., 35: L08607, doi:10.1029/2007GL032838.
Furtado J C, Di Lorenzo E, Schneider N, et al. 2011. North Pacific decadal variability and climate change in the IPCC AR4 models [J]. J. Climate, 24(12): 3049–3067.
Li Chunhui, Wan Qilin, Lin Ailan, et al. 2009. Interdecadal variations of precipitation and temperature in China around the abrupt change of atmospheric circulation in 1976 [J]. Acta Meteorologica Sinica, 23 (3):315–326.
刘秦玉, 李春, 胡瑞金. 2010. 北太平洋的年代际振荡与全球变暖 [J].气候与环境研究, 15 (2): 217–224. Liu Qinyu, Li Chun, Hu Ruijin.2010. Interdecadal oscillations in the North Pacific and the global warming [J]. Climatic and Environmental Research (in Chinese), 15 (2):217–224.
Liu Z Y. 2012. Dynamics of interdecadal climate variability: A historical perspective [J]. J. Climate, 25: 1963–1995.
卢姁, 张东凌. 2009a. 热带太平洋10月份海气联合复EOF分析 [J]. 海洋通报, 28 (5): 54–63. Lu Xu, Zhang Dongling. 2009a. CEOF analysis for coupled circulation of atmosphere and ocean of tropical Pacific Ocean in October [J]. Mar. Sci. Bull. (in Chinese), 28 (5): 54–63.
卢姁, 张东凌. 2009b. 热带太平洋5月份上层洋流的动力统计诊断 [J].热带海洋学报, 28 (2): 22–30. Lu Xu, Zhang Dongling. 2009b. A statistical diagnosis of upper-ocean currents in tropical Pacific Ocean in May [J]. J. Trop. Oceanogr. (in Chinese), 28 (2): 22–30.
卢姁, 张东凌. 2010. 10月份热带印度洋海气耦合的统计动力诊断 [J].大气科学, 34 (2): 351–360. Lu Xu, Zhang Dongling. 2010. Dynamic statistic analysis of coupled circulation of atmosphere and ocean in the tropical Indian Ocean in October [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 34 (2): 351–360.
路凯程, 廖前锋, 张铭. 2011. 赤道外北太平洋冬夏海温场的 EOF分析[J]. 海洋预报, 28 (5): 50–60. Lu Kaicheng, Liao Qianfeng, Zhang Ming. 2011. EOF analysis on sea temperature field in the extratropical North Pacific [J]. Marine Forecasts (in Chinese), 28 (5): 50–60.
吕庆平, 张铭. 2012. 正压海洋对中纬西风响应的解析解及讨论 [J]. 解放军理工大学学报(自然科学版), 13 (5): 583–588. Lü Qingping,Zhang Ming. 2012. Barotropic ocean model forced by mid-latitude time-varying wind [J]. Journal of PLA University of Science and Technology (Natural Science Edition) (in Chinese), 13 (5): 583–588.
吕庆平, 张维锋, 张铭. 2013a. 两层海洋对风场气候异常响应的解析解及其讨论 [J]. 气候与环境研究, 18 (1): 124–134. Lü Qingping, Zhang Weifeng, Zhang Ming. 2013a. Study of two-layer ocean model forced by climate wind anomalies [J]. Climatic and Environmental Research (in Chinese), 18 (1): 124–134.
吕庆平, 路凯程, 张铭. 2013b. 北太平洋冬季上层海温异常的NPGO模态 [J]. 气候与环境研究, 18 (2): 210–220. Lü Qingping, Lu Kaicheng,Zhang Ming. 2013b. NPGO mode of the upper sea temperature anomalies in the North Pacific during winter [J]. Climatic and EnvironmentalResearch (in Chinese), 18 (2): 210–220.
Mantua N J, Hare S R, Zhang Y, et al. 1997. A Pacific interdecadal climate oscillation with impacts on salmon production [J]. Bull. Amer. Meteor.Soc., 78 (6): 1069–1079.
Qiu B, Chen S M. 2006. Decadal variability in the large-scale sea surface height field of the South Pacific Ocean: Observations and causes [J]. J.Phys. Oceanogr., 36: 1751–1762.
Qiu B, Chen S M. 2010. Eddy-mean flow interaction in the decadally modulating Kuroshio Extension system [J]. Deep-Sea Res. Pt. Ⅱ, 57(13–14): 1098–1110.
谭桂容, 孙照渤, 闵锦忠, 等. 2009. 北太平洋海温异常的空间模态及其与东亚环流异常的关系 [J]. 大气科学, 33 (5): 1038–1046. Tan Guirong, Sun Zhaobo, Min Jinzhong, et al. 2009. Spatial modes of summer SST anomaly in North Pacific and its relationship with the circulation anomaly over East Asia [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 33 (5): 1038–1046.
Trenberth K E, Hurrell J W. 1995. Decadal Climate Variations in the Pacific,National Research Council, Natural Climate Variability on Decade-to-Century Time Scales [M]. Washington D C: National Academy Press, 472–481.
吴德星, 林霄沛, 万修全, 等. 2006. 太平洋年代际变化研究进展浅析[J]. 海洋学报, 28 (1): 1–8. Wu Dexing, Lin Xiaopei, Wan Xiuquan, et al. 2006. Progress and perspective in study on interdecadal variability of the Pacific Ocean [J]. Acta Oceanologica Sinica (in Chinese), 28 (1):1–8.
杨修群, 朱益民, 谢倩, 等. 2004. 太平洋年代际振荡的研究进展 [J].大气科学, 28 (6): 979–992. Yang Xiuqun, Zhu Yimin, Xie Qian, et al.2004. Advances in studies of Pacific decadal oscillation [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 28 (6): 979–992.
朱艳峰,丁裕国,何金海. 2002. 中低纬海气相互作用的耦合型态及其年代际振荡特征研究 [J]. 热带气象学报,18 (2): 139–147. Zhu Yanfeng, Ding Yuguo, He Jinhai, 2002. Study the coupled pattern of middle–low air/sea interaction and its decadal varivation [J]. Journal of Tropical Meteorology (in Chinese), 18 (2):139–147.
张东凌, 何卷雄. 2005. 热带印度洋上层洋流的动力统计诊断 [J]. 气候与环境研究, 10 (3): 387–400. Zhang Dongling, He Juanxiong, 2005.Dynamic statistic diagnosis of upper current in tropical Indian Ocean [J].Climatic and Environmental Research (in Chinese), 10 (3): 387–400.
张东凌, 曾庆存. 2007. 5月热带印度洋大气大洋耦合环流的统计动力分析 [J]. 中国科学D辑, 37 (12): 1693–1699. Zhang Dongling, Zeng Qingcun. 2007. Dynamic statistic analysis of coupled ocean–atmosphere circulation of tropical Indian Ocean in May [J]. Science in China (Series D) (in Chinese), 37 (12): 1693–1699.
张东凌, 何卷雄, 曾庆存. 2005. 南海季风爆发的统计动力分析 [J]. 气候与环境研究, 10 (3): 377–386. Zhang Dongling, He Juanxiong, Zeng Qingcun. 2005. Statistic dynamic analysis on the South China Sea monsoon onset [J]. Climatic Environmental Research (in Chinese), 10 (3):377–386.
张永垂, 张立凤. 2009. 北太平洋Rossby波研究进展 [J]. 地球科学进展,24 (11): 1219–1228. Zhang Yongchui, Zhang Lifeng. 2009. Rossby waves in the North Pacific Ocean: A review [J]. Advance in Earth Science(in Chinese), 24 (11): 1219–1228.
Zhang Y C, Zhang L F, Luo Y. 2010. The coupled mode between the Kuroshio region marine heating anomaly and the North Pacific atmospheric circulation in wintertime [J]. J. Trop. Meteor., 16 (1): 51–58.
Zhang Y C, Zhang L F, Lü Q P. 2011. Dynamic mechanism of interannual sea surface height variability in the North Pacific subtropical gyre [J].Adv. Atmos. Sci., 28 (1): 158–168.

