基于理论地震图方法的波导结构对地下核爆炸Lg波传播特性研究

何永锋 李 锴 刘炳灿 姚国政赵克常 张献兵 曾乐贵

1）中国北京100072装甲兵工程学院

2）中国北京100871北京大学地球与空间科学学院

引言

高质量的数字地震记录波形数据，增强了人们对地壳结构以及震源过程对地震波信号影响机制的认识.地震学家们致力于建立一维和三维的精细地球介质模型.该精细介质模型对地震定位及解释地壳物理结构的变化具有重要意义，如IASP91模型就是其中一个典型代表（Kennett，Engdahl，1991）.

由于地球结构具有非均匀性以及球体和分层的特性，所以对不同区域的地震波进行研究时，区域性的地球结构是不可忽略的重要因素.科研人员也建立了许多区域性的模型来解释由传播所造成的波形复杂性，尤其是短周期成分的复杂性（Dreger，Helmberger，1991；Vogfjord，Langston，1991；Zhao，Helmberger，1991；Saikia et al，1992，1994；何永锋等，2010）.Saikia和Burdick（1991）的研究结果表明，利用层结构间射线干涉和叠加理论可以很好地解释Pnl震相中的短周期成分.

图1 前苏联东哈萨克斯坦地区地下核试验在乌鲁木齐台站记录的地震波形图Fig.1 Seismograms of underground nuclear explosions at a former Soviet test site located at eastern Kazakhstan recorded by the WMQ station

区域台网的地震记录波形信号中，Lg波是常见的震相.图1所示是震中距为950km的乌鲁木齐台站记录的前苏联东哈萨克斯坦的3次地下核试验地震波的垂向分量的波形图，震级分别为mb＝5.82，5.90，6.10.可以看出，尽管震中位置（见图1所示的震中坐标）和震源强度不同，但Lg波的波列分布特征相似，波列持续时间相近.这说明，该地下核试验场区域沿乌鲁木齐台站路径的波导结构是相似的.

Lg波是与地壳浅层结构有密切关系的面波或导波.对于Lg波的成因，目前还存在争论，主要有两种观点：一种观点认为Lg波是高阶面波频散曲线的叠加；另一种观点则认为它是地壳低速层中的导波，由于其能量被限制在地壳低速层中，振幅随传播距离衰减得较慢，故称之为导波（刘斌，2009）.Lg波是大陆型地壳结构中所特有的地震波，当地震波的传播路径包含海洋性地壳或山脉型地壳时，地震波的能量会发生强烈的衰减，因此在稳定的大陆地区（如前苏联的东哈萨克斯坦核试验场），Lg波相对稳定，并且振幅较大，是用来研究震源特性及传播效应的重要震相.本文利用基于广义反射和透射系数的频率－波数域算法来研究地壳波导结构对区域震相高频成分的影响，进而分析区域震相Lg波的演化机理，为深入理解Lg波提供一种途径.

数值方法模拟计算不同模型下的理论地震波形图，是分析地下核爆炸的区域震相特征及震源机制的有力手段.为了模拟高频地震波信号，利用频率－波数域（f-k）积分方法（Fuchs，Müller，1971；Kind，1979；Kennett，1980；Bouchon，1981；Yao，Harkrider，1983；Chen，1993）对傅里叶－贝塞尔变换进行积分.该算法的最大优点是能够模拟出全波场震相，其中包括复杂分层速度结构中的导波.

理论地震图方法是加深理解Lg波的激发机制和传播规律的一个重要途径，其中以Olsen等（1983）、Campillo等（1984）及Kim（1987）的工作为典型代表.实际地表可能存在侵入式的不连续速度变化结构或速度梯度结构，这都可能成为激发Lg波的波导.Campillo和Paul（1992）的研究结果表明，浅地表速度随深度扰动分布的薄层叠加结构，对Lg波的激发具有很大的影响.作者曾对壳幔过渡带速度梯度结构对首波的影响进行了研究（何永锋等，2010），结果表明速度梯度对首波幅度随震中距的变化具有明显的影响.实际地壳分层并非平坦，接收台站处的地壳也并非具备各向同性的分层结构.基于三维模型的数值分析表明，Lg波波尾的形成或许与接收点处的壳层结构随机分布有关（Frankel，Clayton，1984；Wu，1985），或者与接收点处地壳分层非一致性有关（Barker et al，1981；Kawase，Aki，1989）.基于散射近似理论（Tolstoy，Clay，1966），Aki和Chouet（1975）认为由速度结构的随机分布而导致的逆向散射地震波是形成Lg波波尾的主要因素.介质的不均匀性导致的散射效应QS是地震波能量随距离衰减的主要因素，同时介质本身固有的衰减效应QI也是不可忽略的因素.本文利用基于一维模型的频率－波数域算法，对速度梯度结构、速度扰动分布的薄叠加层结构及Q值变化等对前苏联东哈萨克斯坦地下核爆炸激发的Lg波的传播特征进行了理论分析，以期对深入理解及利用Lg波提供参考.

1 速度梯度的影响

图2给出了前苏联东哈萨克斯坦地区地下核试验场至我国乌鲁木齐台站间的地球介质速度模型.其中模型1为Steven模型，是对实际条件下东欧地区地壳的速度取平均，其是以速度的突然变化来达到分层的目的，但实际情况显然不是这样，如可能存在的速度梯度结构.Saikia（1994）对美国内华达地下核爆炸的区域震相的研究结果表明，速度梯度对Lg波具有削弱作用.采用类似方法，将模型1进行修改，在地表10km以内加入速度梯度结构，P波和S波的速度梯度分别为

含有速度梯度和速度扰动分布的模型结构分别如图2b和图2c所示.

从震源的角度来说，激发地下核爆炸Lg波的主要因素是伴随地下核爆炸层裂过程特有的辅助源——线性矢量偶极源（compensate linear vector dipole，简写为CLVD）（Patton，1991；何永锋等，2005，2012）.图3为基于东哈萨克斯坦地壳速度模型（模型1）（McLaughlin et al，1988）下CLVD源激发的理论地震波形图（0—3Hz），震源深度分别为300，600，900m，震中距为950km.图3为不同埋藏深度下CLVD源激发的理论地震波形图，可以看出，Lg波十分发育.从能量角度来看，CLVD源适合作为激发地下核爆炸低频Lg波的主要源，其空间分布特征有利于S波的形成，即对角分量的偏差直接激发了S波.与实际波形图比较，可以看出基于模型1的数值模拟结果中Lg波能量偏大，与实际情况不符.

图2 （a）Steven模型；（b）速度梯度分布模型；（c）速度扰动分布模型Fig.2 （a）Steven model；（b）Velocity gradient model；（c）Velocity perturbation model

图3 基于模型1（a）和模型2（b）介质速度模型的理论地震波形图Fig.3 Theoretical seismograms based on the velocity of Steven model（a）and velocity gradient model（b）

基于模型2的理论地震波形图如图3b所示.可以看出，速度梯度波导结构对Lg波具有明显的削弱作用.与图1相比较，其数值模拟结果与实际波形图更相符，对Rg波的削弱作用不明显，这与Rg波形成机制相符.该结果可以从理论上说明，前苏联东哈萨克斯坦地下核试验场至我国新疆乌鲁木齐台站间的传播路径中的速度梯度结构可能是影响区域震相的一个重要因素.

2 速度扰动分布的薄叠加层结构的影响

模型1中层间速度突变与实际情况不符，实际地壳中可能存在由侵入体造成的速度扰动分布的波导结构，此结构可以利用速度随深度扰动分布的薄叠加层结构来表示.该方法最早由Richards和Menke（1983）提出，用来研究散射效应.如图2中模型3所示，在地表及壳幔过渡带中引入速度随机分布的薄层结构.基于模型3的理论地震波形模拟结果如图4b所示，该结构对Lg波同样具有削弱作用.与模型1结果不同的是，该结构还可以使Lg波波列变宽，可以模拟出Lg波的波尾，这与实际波形更加相符.这说明速度扰动分布的波导结构符合前苏联东哈萨克斯坦地下核试验场至我国新疆乌鲁木齐台站间的传播路径，速度扰动分布可能是影响区域震相的重要因素之一.

图4 基于模型1（a）和模型3（b）介质速度模型的理论地震波形图Fig.4 Theoretical seismograms based on the velocity of Steven model（a）and velocity perturbation model（b）

3 Q值的影响

基于东欧地区给出的模型1中的Q值比较高，如表1所示，数值模拟结果中的Lg波能量偏大，与实际情况不符.由速度变化引起的散射效应会对区域震相Lg波产生影响，由于实际地球的地壳乃至地幔上部的横向变化较大，因而地球浅层的Q值会因地区而异.对区域的地震波衰减问题，需要引用对特定区域Q值的专门研究结果（樊计昌等，2001；徐彦等，2005）.基于此，对模型1中的QS值进行修正，结果列于表1.

基于QS修正模型的理论地震波形如图5b所示.可以看出：修正后的QS对Lg波具有明显的削弱作用，与实际观测数据相符；同时还可以看出，QS值对Lg波的影响要远远大于对Pg波的影响.据此可以推断，Lg波的衰减特性反映了地球介质的固有衰减机制，可以利用此方法对地球介质中某区域的Lg波衰减值进行测量，得到介质本身固有的衰减效应QI.

表1 东哈萨克斯坦地区地下核试验场区速度模型Table 1 Seismic velocity model of underground nuclear test site at eastern Kazakhstan region

图5 基于模型1（a）和修正QS（b）的介质速度模型的理论地震波形图Fig.5 Theoretical seismograms based on the Steven model（a）and revised Steven model with modified QSvalue（b）

为考察速度扰动分布和Q值变化对区域震相Lg波的综合影响，对模型3中的QS值进行了如表1所示的修正，数值计算了CLVD源在该模型下的理论地震图，其结果如图6所示（震源深度分别为300，600，900m）.可以看出，综合效应不仅削弱了Lg波，使Lg波列进一步展宽，而且该综合效应有利于Rg波的激发.

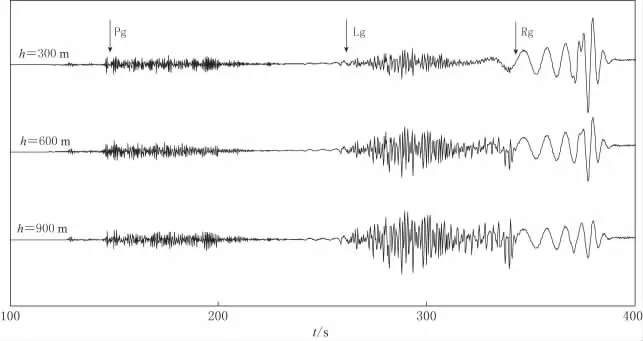
图6 基于模型3的Q值修正介质速度模型的理论地震波形图Fig.6 Theoretical seismograms based on the perturbation model with modified Qvalue

4 讨论与结论

区域震相Lg波在稳定的大陆地区十分发育且很稳定，通常是区域地震图上幅值最大的震相，在地下核爆炸地震学中越来越被人们所重视，如在识别和当量估计等方面，其效果要比体波稳定.实际记录波形资料表明，我国乌鲁木齐台站对前苏联东哈萨克斯坦地下核试验场所实施的地下核爆炸实验具有很好的检测能力，区域震相Lg波明显，为利用Lg波进一步分析地下核爆炸地震波形特征奠定了基础.基于东欧地区的模型1（Steven模型），能够数值模拟出能量很高的Lg波，这与实际观测结果不符，说明该模型过于简单.为此本文首先引入速度梯度结构，数值模拟结果表明速度梯度对Lg波具有削弱作用；然后在地表和壳幔过渡带引入速度扰动分布的薄叠加层结构，基于该结构的理论地震波形图结果表明，该结构不仅可以削弱Lg波，还可以作为Lg波波尾的一种成因；接着文章进一步分析了Q值对Lg波的影响，结果表明，Q值的变化对Lg波的影响要远大于对体波的影响；最后对速度扰动及Q值变化的综合影响进行分析，综合效应显示，Lg波不仅被削弱，且使波列进一步加宽.

本文在前苏联东哈萨克斯坦地下核试验场至我国新疆乌鲁木齐台站间的地球介质模型中引入速度梯度结构、速度扰动分布的薄叠加层结构、降低Q值结构以及速度扰动与Q值变化综合结构，在震源模型固定的前提下，分别数值模拟出与实际情况相符的理论地下核爆炸地震波形，结果表明不同的波导结构对区域震相Lg波的传播具有重要影响.实际的路径效应应该为各种因素的综合效果.速度扰动分布与Q值变化综合效应分析结果表明，综合效果与实际观测结果更加符和.

樊计昌，李松林，赖晓玲，邓宏钊.2001.新疆伽师地震区三维Q值结构［J］.地震学报，23（6）：573－－581.

Fan J C，Li S L，Lai X L，Deng H Z.2001.Three-dimensional Qstructure in Jiashi earthquake region of Xinjiang region［J］.Acta Seismologica Sinica，23（6）：573－－581（in Chinese）.

何永锋，陈晓非，张海明.2005.地下核爆炸Lg波的激发机制［J］.地球物理学报，48（2）：367－－372.

He Y F，Chen X F，Zhang H M.2005.The excitation of Lg wave by underground nuclear explosions［J］.Chinese Journal of Geophysics，48（2）：367－－372（in Chinese）.

何永锋，赵克常，张献兵.2010.地下核爆炸的主要非爆炸源机制［J］.地球物理学进展，25（3）：789－－794.

He Y F，Zhao K C，Zhang X B.2010.Primary non-explosive source mechanisms for underground nuclear explosions［J］.Progress in Geophysics，25（3）：789－－794（in Chinese）.

何永锋，赵克常，张献兵，马裕然，王洋.2012.地下核爆炸地震波二次源特征［J］.地球物理学报，55（5）：1742－－1748.

He Y F，Zhao K C，Zhang X B，Ma Y R，Wang Y.2012.The characteristic of the waveform from the second source induced by underground explosion［J］.Chinese Journal of Geophysics，55（5）：1742－－1748（in Chinese）.

刘斌.2009.地震学原理与应用［M］.合肥：中国科学技术大学出版社：72－－74.

Liu B.2009.Principles and Applications of Seismology［M］.Hefei：Press of University of Science and Technology of China：72－－74（in Chinese）.

徐彦，毛燕，胡家富，苏有锦，丛连理.2005.新疆及周边地区Lg尾波的Q值分布［J］.地震学报，27（2）：155－－162.

Xu Y，Mao Y，Hu J F，Su Y J，Cong L L.2005.Distribution of Lg coda Qvalue in Xinjiang and its adjacent regions［J］.Acta Seismologica Sinica，27（2）：155－－162（in Chinese）.

Aki K，Chouet B.1975.Origin of coda waves：Source，attenutation，and scattering effects［J］.J Geophys Res，80（23）：3322－－3342.

Barker B W，Der Z A，Mrazek C F.1981.The effect of crustal structure on the regional phases Pg and Lg at the Nevada test site［J］.J Geophys Res，86（B3）：1686－－1700.

Bouchon M.1981.A simple method to calculate Green’s functions for elastic layered media［J］.Bull Seismol Soc Am，71（4）：959－－971.

Campillo M，Bouchon M，Massinon B.1984.Theoretical study of the excitation，spectral characteristics，and geometrical attenuation of regional seismic phases［J］.Bull Seismol Soc Am，74（1）：79－－90.

Campillo M，Paul A.1992.Influence of the lower crustal structure on the early coda of regional seismograms［J］.J Geophys Res，97（B3）：3405－－3416.

Chen X F.1993.A systematic and efficient method of computing normal modes for multilayered half-space［J］.Geophys J Int，115（2）：391－－409.

Dreger D S，Helmberger D V.1991.Complex faulting deduced from broadband modeling of the 28February 1990Upland earthquake（ML＝5.2）［J］.Bull Seismol Soc Am，81（4）：1129－－1144.

Frankel A，Clayton R W.1984.A finite-difference simulation of wave propagation in two-dimensional random media［J］.Bull Seismol Soc Am，74（6）：2167－－2186.

Fuchs K，Müller G.1971.Computation of synthetic seismograms with the reflectivity method and comparison with observations［J］.Geophys J Int，23（4）：417－－433.

Kawase H，Aki K.1989.A study on the response of a soft basin for incident S，P，and Rayleigh waves with special reference to the long duration observed in Mexico city［J］.Bull Seismol Soc Am，79（5）：1361－－1382.

Kennett B L N.1980.Seismic waves in a stratified half space：Ⅱ.Theoretical seismograms［J］.Geophys J Int，61（1）：1－－10.

Kennett B L N，Engdahl E R.1991.Traveltimes for global earthquake location and phase identification［J］.Geophys J Int，105（2）：429－－465.

Kim W Y.1987.Modelling short-period crustal phases at regional distances for the seismic source parameter inversion［J］.Phys Earth Planet Inter，47：159－－178.

Kind R.1979.Extensions of the reflectivity method［J］.J Geophys Res，45：373－－380.

McLaughlin K L，Barker T G，Day S M，Shkoller B，Stevens J L.1988.Effects of Depth of Burial on Explosion and Earthquake Regional Seismograms：Regional Discrimination and Yield Estimation［R］.S-CUBED report No.SSSR-88-9844，Jolla，California.

Olsen K H，Braile L W，Stewart J N.1983.Modeling short-period crustal phases（P，Lg）for long-range refraction profiles［J］.Phys Earth Planet Inter，31（4）：334－－347.

Patton H J.1991.Seismic moment estimation and the scaling of the long－period explosion source spectrum［G］∥AGU Geophysical Monograph 65：Explosion Source Phenomenology：239－－252.

Richards P G，Menke W.1983.The apparent attenuation of a scattering medium［J］.Bull Seismol Soc Am，73（4）：1005－－1021.

Saikia C K，Burdick L J.1991.Fine structure of Pnlwaves from explosions［J］.J Geophys Res，96（B9）：14383－－14401.

Saikia C K，Helmberger D V，Burdick L J.1992.Regional wave propagation and high-frequency／low-frequency energy level discriminant［C］∥Proceedings of14th Annual PL／DARPA Seismol Res Symp.16—18September，Tucson，Arizona：351－－360.

Saikia C K.1994.Modified frequency-wavenumber algorithm for regional seismograms using Filon’s quadrature：Modelling of Lg waves in eastern North America［J］.Geophys J Int，118（1）：142－－158.

Saikia C K，Dreger D G，Helmberger D V.1994.Modeling of energy amplification recorded within Greater Los Angeles using irregular structure［J］.Bull Seismol Soc Am，84（1）：47－－61.

Tolstoy I，Clay C S.1966.Ocean Acoustics Theory and Experiment in Underwater Sound［M］.New York：McGraw-Hill.

Vogfjord K S，Langston C A.1991.Analysis of regional events recorded at NORESS［J］.Bull Seismol Soc Am，80（6B）：2016－－2031.

Wu R S.1985.Multiple scattering and energy transfer of seismic waves-separation of scattering effect from intrinsic attenuation：Ⅰ.Theoretical modeling［J］.Geophys J Int，82（1）：57－－80.

Yao Z X，Harkrider D G.1983.A generalized reflection-transmission coefficient matrix and discrete wavenumber method for synthetic seismograms［J］.Bull Seismol Soc Am，73（6A）：1685－－1699.

Zhao L S，Helmberger D V.1991.Broadband modelling along a regional shield path，Harvard recording of the Saguenay earthquake［J］.Geophys J Int，105（2）：301－－312.