Solution of Fully Fuzzy System of Linear Equations by Linear Programming Approach

Diptiranjan Behera,Hong-Zhong Huangand S.Chakraverty

Solution of Fully Fuzzy System of Linear Equations by Linear Programming Approach

Diptiranjan Behera1,2,Hong-Zhong Huang1and S.Chakraverty3

Fuzzy systems of linear equations play a vital role in various applications of engineering,science and finance problems.This paper proposes a new method for solving Fully Fuzzy System of Linear Equations(FFSLE)using the linear programming problem approach.There is no restriction on the elements of coefficient matrix.The proposed method is able to solve the system,when the elements of the fuzzy unknown vector are both non-negative and non-positive.Triangular convex normalized fuzzy sets are considered for the present analysis.Known example problems are solved and compared with the results of existing methods to illustrate the efficacy and reliability of the proposed method.

Linear programming,Triangular fuzzy number,Fully fuzzy system of linear equations

1 Introduction

System of linear equations has great applications in various areas such as operational research,physics,statistics,engineering and social sciences.Equations of this type are necessary to solve for the involved parameters.A general real system of linear equations may be written asAX=b,where,Aandbare crisp real matrix andXis unknown real vector.It is simple and straight forward when the variables involving the system of equations are crisp numbers.But in actual case the parameters may be uncertain or a vague estimation about the variables are known as those are found in general by some observation,experiment or experience.So,to overcome the uncertainty and vagueness,one may use the fuzzy numbers in place of the crisp numbers.Thus the crisp system of linear equations becomes a Fuzzy System of Linear Equations(FSLE)or Fully Fuzzy System of Linear Equations(FFSLE).There is a difference between fuzzy linear system and fully fuzzy linear system.The coefficient matrix is treated as crisp in the fuzzy linear system,but in the fully fuzzy linear system all the parameters and variables are considered to be fuzzy numbers.It is an important issue to develop mathematical models and numerical techniques that would appropriately treat the general fuzzy or fully fuzzy linear systems because subtraction and division of fuzzy numbers are not the inverse operations to addition and multiplication respectively.So,this is an important area of research in the recent years.As such in the following paragraph few related literatures are reviewed for the sake of completeness of the problem.

The concept of fuzzy set and fuzzy number were first introduced by Zadeh(1965).Related to fuzzy sets several excellent books have also been written by different authors[Hanss(2005);Zimmermann(2001);Ross(2004);Kaufmann and Gupta(1985);Dubois and Prade(1980)].We know that fuzzy number arithmetic is widely applied in computation of linear system of equations,whose parameters are represented by fuzzy numbers,has a great importance.Solution of a generalised FSLE was first proposed by Friedman,Ming,and Kandel(1998),whose coefficient matrix and right-hand side column vector are defined as crisp and fuzzy respectively.Moreover some methods for solving this type of system can be found in[Chakraverty and Behera(2013);Behera and Chakraverty(2012a);Behera and Chakraverty(2013c);Abbasbandy and Jafarian(2006);Abbasbandy,Jafarian,and Ezzati(2005);Allahviranloo(2004,2005);Sun and Guo(2009);Yin and Wang(2009);Gong and Guo(2011)].Also these types of system are applied to find the static responses of structures using fuzzy finite element method[Behera and Chakraverty(2013b)].

However FFSLE, was also studied by few authors. As such Behera and Chakraverty (2015); Das and Chakraverty (2012) have studied the solution procedure for fullyfuzzy system of linear equations, where the authors have considered all the involved parameters as positive.A numerical approach based on Cholesky decomposition is described by Senthilkumar and Rajendran(2011)to find the positive solution of a symmetric fully fuzzy linear system.Recently,Babbar,Kumar,and Bansal(2013)proposed a new method to find the non-negative solution of a fully fuzzy linear system,where the elements of the coefficient matrix are defined as arbitrary triangular fuzzy numbers of the form(m,α,β).Dehghan and Hashemi(2006);Dehghan,Hashemi,and Ghatee(2007)have proposed the adomian decomposition method,iterative methods and some computational methods such as Cramer’s rule,Gauss elimination method,LU decomposition method and linear programming approach for finding the solutions of fully fuzzy system of linear equations.Muzzioli and Reynaerts(2007)investigated the non-negative solution procedure of fuzzy system by non-linear programming approach.Otadi and Mosleh(2012)applied a linear programming approach to find the non-negative solution of a fully fuzzy matrix equation whose elements of the coefficient matrix are considered as arbitrary triangular fuzzy numbers.There are no restrictions about the elements of the coefficient matrix of the corresponding system.Allahviranloo and Mikaeilvand(2011)discussed fully fuzzy system of linear equations by using the embedding approach.Allahviranloo,Salahshour,and Khezerloo(2011)proposed the maximal and minimal symmetric solutions of fully fuzzy linear systems.Recently Allahviranloo,Hosseinzadeh,Ghanbari,Haghi,and Nuraei(2013)also studied a new approach for fuzzy trapezoidal solution,namely “suitable solution”,for a fully fuzzy linear system(FFLS)based on solving two fully interval linear systems(FILSs)that are 1-cut and 0-cut of the related fuzzy interval systems.Moreover an approximate solution of dual fuzzy matrix equations has been analyzed by Gong,Guo,and Liu(2014)recently.Also Behera and Chakraverty(2013a)have applied FFSLE for the uncertain static responses of structures using fuzzy finite element method.However Yang,Li,and Cai(2013)have considered both random and fuzzy variables for the structural reliability.

In the following sections first basic preliminaries are given.Then a new method is proposed to solve fully fuzzy system of linear equations using the linear programming approach.Next,numerical examples are solved using the proposed method.Lastly conclusions are drawn.

2 Preliminaries

In this section,some notations,definitions and preliminaries related to the present work are given[Kaufmann and Gupta(1985);Zimmermann(2001);Ross(2004);Behera and Chakraverty(2012a,2014);Otadi and Mosleh(2012);Fatullayev and Koroglu(2012)].

Definition 2.1(Fuzzy number).Fuzzy numberis a convex normalized fuzzy setof the real lineRsuch thatwhere,is called the membership function of the fuzzy set and it is piecewise continuous.

Definition 2.2(Triangular fuzzy number).Triangular fuzzy number˜uis a convex normalized fuzzy set˜uof the real lineRsuch that

Let us consider an arbitrary triangular fuzzy number=(a,b,c).The membership functionofwill be define as follows

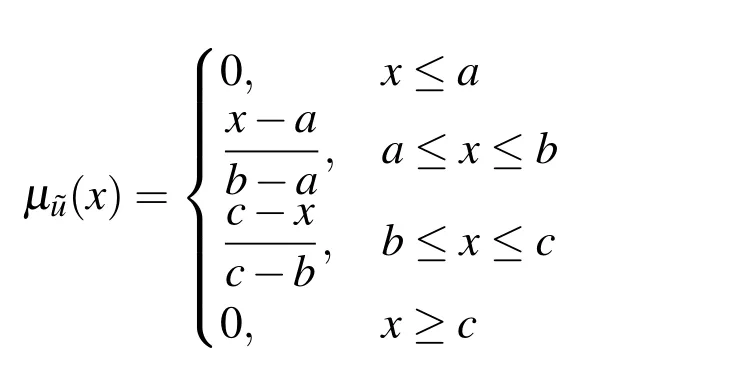
Definition 2.3.Non-negative(Non-positive)triangular fuzzy number A triangular fuzzy number=(a,b,c)is said to be non-negative(non-positive)ifa≥0(c≤0).

Definition 2.4.Fuzzy arithmetic Let=(a,b,c)and=(e,f,g)be two triangular fuzzy numbers.Then fuzzy arithmetic is defined as below

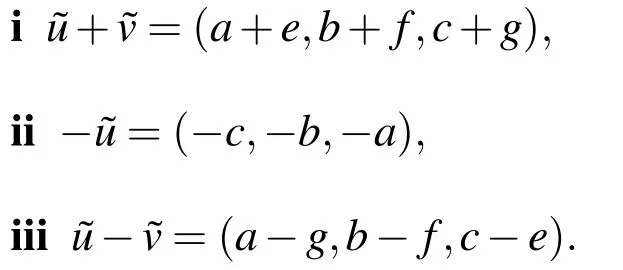
Multiplication of two arbitrary fuzzy numbers is denoted as[Otadi and Mosleh(2012)]

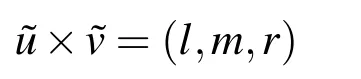
where,l=min(ae,ag,ce,cg),m=bfandr=max(ae,ag,ce,cg).

Two triangular fuzzy numbers=(a,b,c)and=(e,f,g)are said to be equal if and only ifa=e,b=fandc=g.

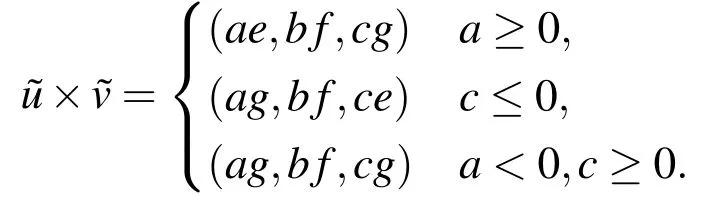
3 Fully fuzzy system of linear equations and the proposed method

Then×nfully fuzzy system of linear equations may be written as

In matrix notation above system may be written as

where,the coefficient matrixnis a fuzzyn×nmatrix of triangular fuzzy numbers,is a column vector of triangular fuzzy number andnis the vector of fuzzy unknown,where

Let us now denote the triangular fuzzy number matrix elements such asand

So Eq.(3)may be written as

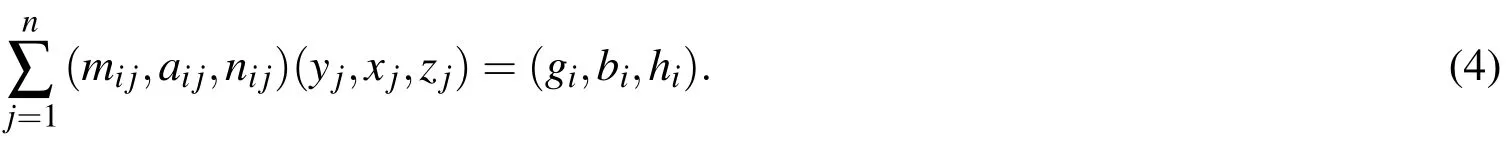
If in then×nfully fuzzy system of linear equations(2),each element ofandis a non-negative fuzzy number,then we call the system(2)a non-negative FFSLE.

Definition 3.1.Consider a non-negative FFSLE as defined in Eq.(3).We say thatis a non-negative fuzzy solution vector if

Moreover ifyj≥0,xj-yj≥0 andzj-xj≥0 then we say thatis a consistent solution of the FFSLE.

Letmij=M,aij=A,nij=N,gi=g,bi=b,hi=h,yj=Y,xj=Xandzj=Z.

Hence system(5)can be written in matrix form as

From this one may get the solution as

ifM,A,andNare nonsingular.

Next a theorem is stated and proved as follows for the existence of solution.This is the special case of the theorem proved by Otadi and Mosleh(2012).

Theorem 3.2.Let=(M,A,N)≥0,=(g,b,h)≥0,and each of the matrices M,A,N be a product of a permutation matrix by a diagonal one.Also let M-1g≤A-1b≤N-1h.Then the non-negative FFSLE(2)has exist anon-negative consistent fuzzy solution.

Proof.Hypothesis imply thatM-1,A-1,N-1exists as non-negative matrices(De-Marr 1972).So we haveY=M-1g≥0,X=A-1b≥0,Z=N-1h≥0 withM-1g≤A-1b≤N-1h.Hence from this one may conclude that˜Xis a non-negative solution of the required system.

Next we will proceed for the proposed method where the components of the elements of the coefficient matrix has no restrictions on their sign.Before this first we will discuss some limitations of the existing methods to have a better idea about the present analysis.

3.1 Limitations of the existing methods

Following are short comings of the existing methods for solving fuzzy and fully fuzzy system of linear equations.

1.There exist different solution procedures[Chakraverty and Behera(2013);Behera and Chakraverty(2012a);Behera and Chakraverty(2013a);Abbasbandy and Jafarian(2006);Abbasbandy,Jafarian,and Ezzati(2005);Allahviranloo(2004,2005);Sun and Guo(2009);Yin and Wang(2009);Friedman,Ming,and Kandel(1998)]for fuzzy system of linear equations where the coefficient matrices are considered as crisp real matrix.It may be noted that these methods are not applicable when system is fully fuzzy.

2.Various methodologies[Das and Chakraverty(2012);Senthilkumar and Rajendran(2011);Dehghan and Hashemi(2006);Dehghan,Hashemi,and Ghatee(2007);Muzzioli and Reynaerts(2007);Otadi and Mosleh(2012);Allahviranloo and Mikaeilvand(2011)]have been proposed to solve FFSLE of the form where all the elements of fuzzymatrices are considered as non-negative.These methods are not able to solve the problem as define in Example 1.

3.Recently Otadi and Mosleh(2012);Babbar,Kumar,and Bansal(2013)proposed solution technique for FFSLE.The components of the elements of the coefficient matrix has no restrictions on their sign.But the methods can only give the non-negative solution.These methods are not applicable when the unknown solution vector consists of only non-positive elements or both non-negative and non-positive elements as considered in Examples 2 and 3.

To overcome the above limitations a new method has been proposed in the following section based on linear programming problem approach.

3.2 Proposed method for solving FFSLE using linear programming

Let us first consider the α-cut representation of the FFSLE(3),

Before proceeding to solve the above system we will first determine the sign of the elements of the solution vector of the main system(1).For this first,we have to find the core of the solution vector.That means we have to solve Eq.(8)for α=1.Hence corresponding system(8)converts to a crisp system of linear equations as

Equivalently the above system can be written as

From Eq. (10) one can get the core solution and may predict the sign of the elements of solution vector by the following proposition.

Proposition 3.3.

Iffor1≤i≤n where,0/∈,then sign of theelements of the fuzzy solution vector can be predicted from the core solution of thecorresponding system by solvingwhereand

Proof.The core solutionxjcan be obtained by solving the crisp system=bi.From this we may get the sign of the elements present in core solution.Also we know that 0/∈and core is the inner point of the fuzzy solution.Hence one may predict the sign of the elements of fuzzy solution vector accordingly.

Next the following propositions are to be used to find whether the sign of the elements of the fuzzy solution vector are non-negative,non-positive or both nonnegative and non-positive.

Proposition 3.4.If the elements of core solution viz.xjfor1≤j≤n,are nonnegative(non-positive)then the elements of fuzzy solution vectorarenon-negative(non-positive).

Proof.The proof of the proposition is straight forward.

Proposition 3.5.If the core solution contains both non-negative and non-positive elements,i.e.xjfor{j∈N|1≤j≤k}are non-negative and for{j∈N|k+1≤j≤n}are non-positive for all i,where1≤i≤n and N is the natural number,then the fuzzy solution vectorfor{j∈N|1≤j≤k}are non-negative and for{j∈N|k+1≤j≤n}are non-positive for all i.

Proof.The proof of the proposition is straight forward.

In general the obtained sign of the elements may be one of the following cases:

We discuss below the solution procedure for all the above cases.

Case 1:In this case we have considered allare non-negative.So,Eq.(4)for this case may be converted to

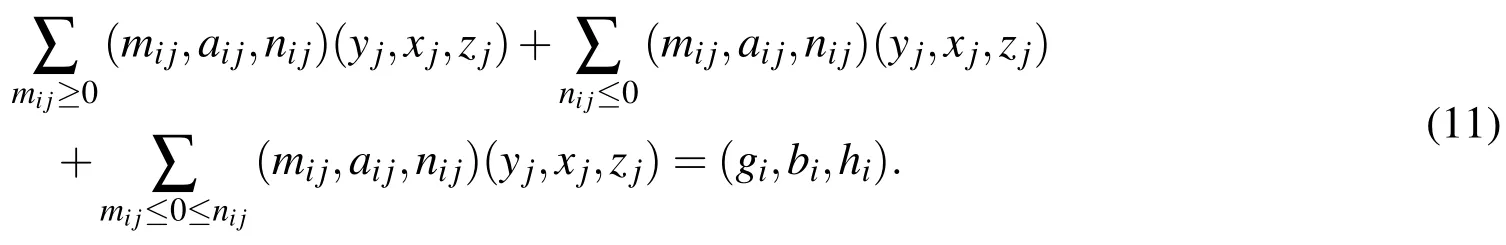
Eq.(11)is now expressed by applying the general rule of fuzzy multiplication as

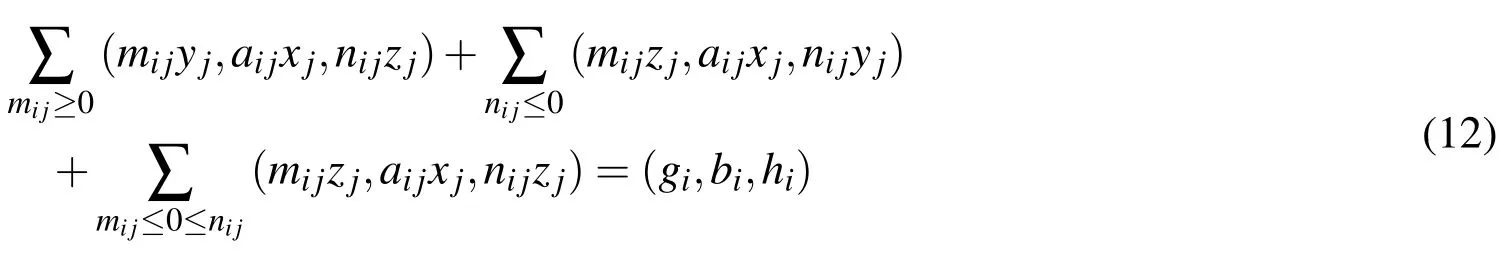
Above equation can be written equivalently

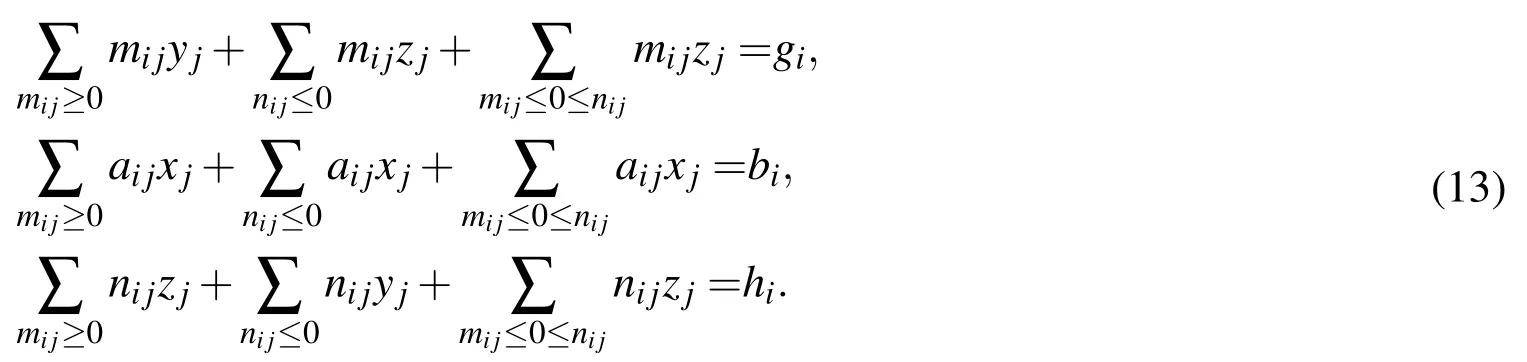
Let us denote the above system as

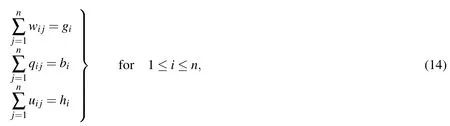
where,

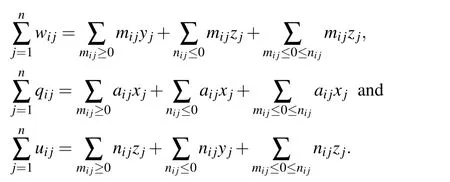
Next one may solve the crisp system(13)directly or may convert Eq.(14)into the following Linear Programming Problem(LPP)to have the solution.For LPP,the artificial variablesrsfors=1,2,···,n,n+1,···3nare introduced.Hence the corresponding LPP can be defined as

Minimize:r1+r2+···+r3n

With the non-negative restrictions,yj,xj,zjandrsfors=1,2,···,n,n+1,···,3n≥0.Standard method may be applied to get the final solution of the fully fuzzy system.

Case 2:Next in this case let us consider allare non-positive.For this case Eq.(4)can similarly be written as

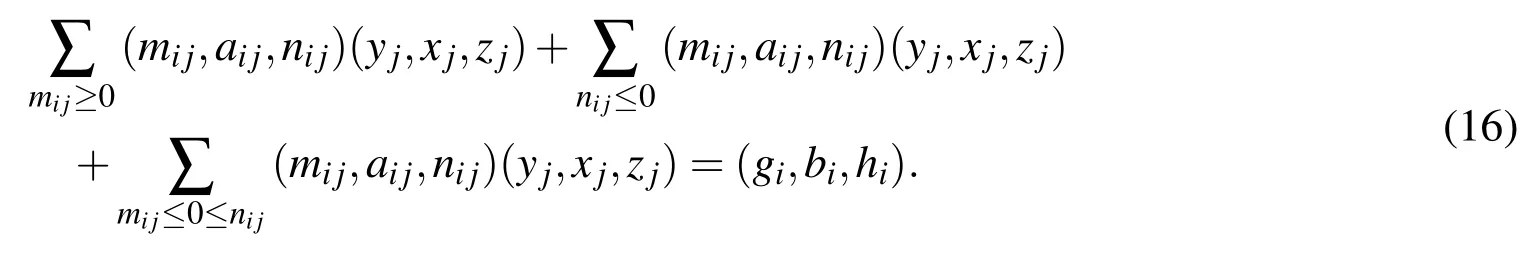
The above equation is now expressed,by changing all non-positive variables to non-negative variables as

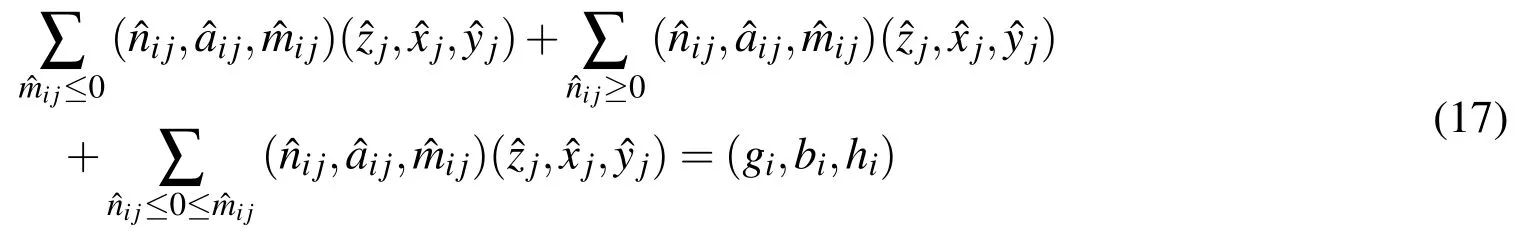
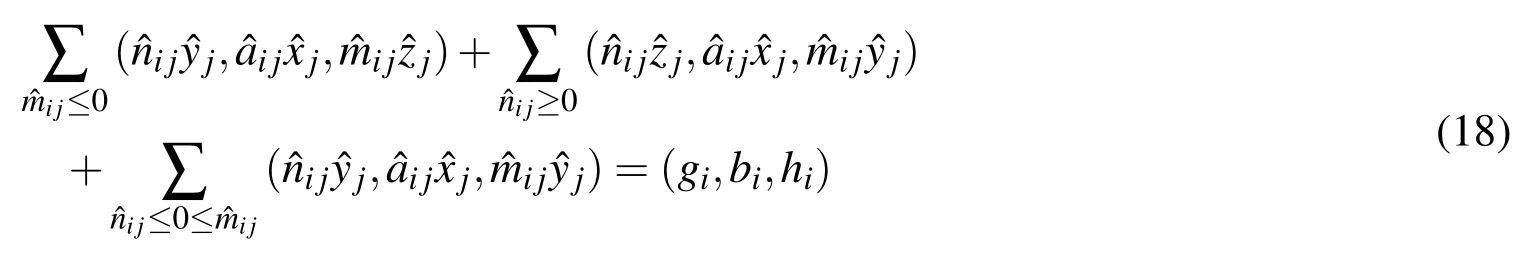
Next we may represent the above system as

where,

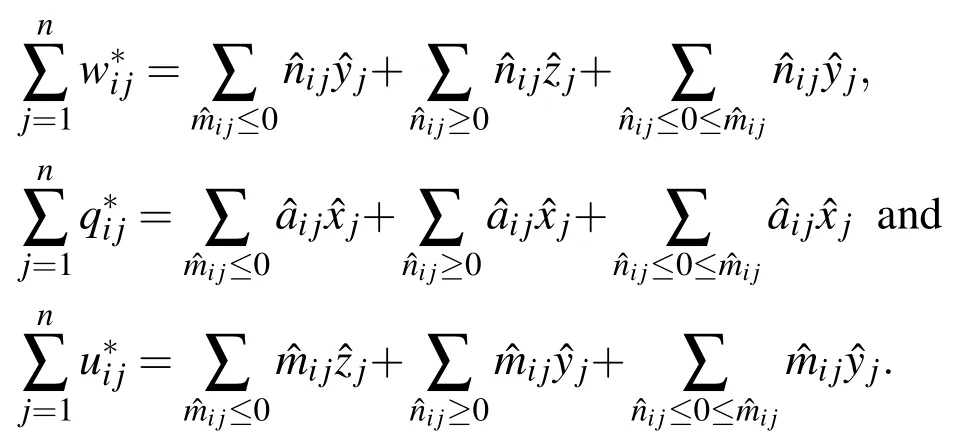
Similarly for the Case 1 one can convert the above system to the following LPP to find the optimum solution

Minimize:r1+r2+···+r3n

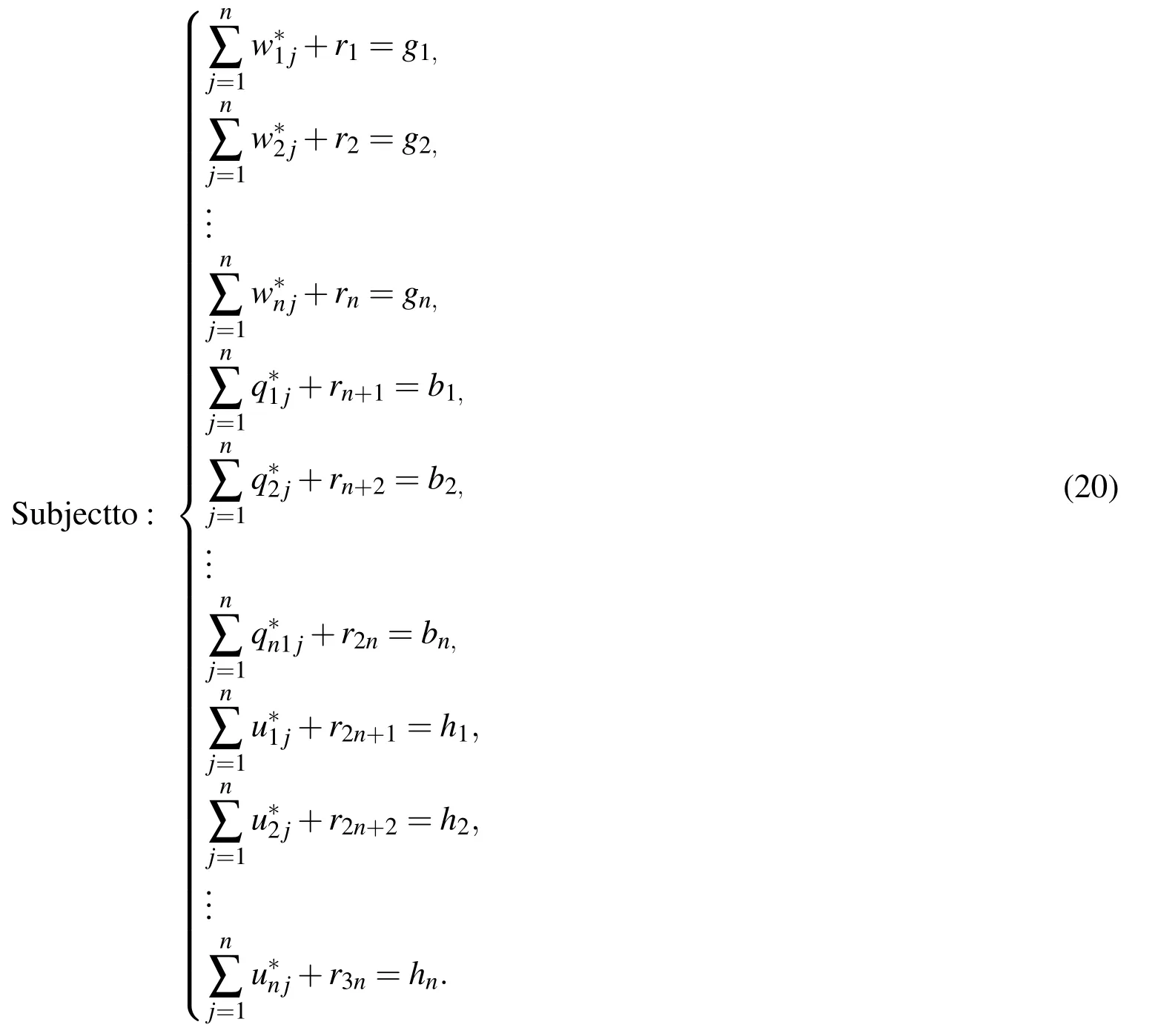
With the non-negative restrictionsandrsfors=1,2,···,n,n+1,···,3n≥0.Now solving the above LPP by any standard method one may have the optimum solution.From which we may obtain the solution of the FFSLE.

Case 3:Finally for this case let us assume the solution vectorcontains both non-negative and non-positive fuzzy numbers.Hence let us consider thatfor{j∈N|1≤j≤k}are non-negative and for{j∈N|k+1≤j≤n}are non-positive for alli,where 1≤i≤nandNis the natural number.Keeping this in mind one may now convert Eq.(4)as

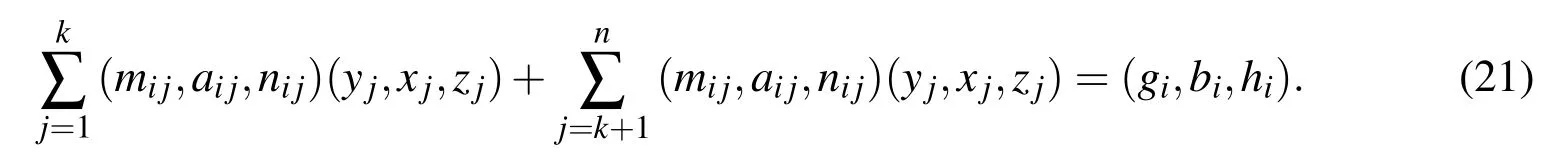
From the discussion of previous two cases,it is possible to write the above expression as follows

Hence corresponding LPP for the above system(23)can be expressed as

Minimize:r1+r2+···+r3n

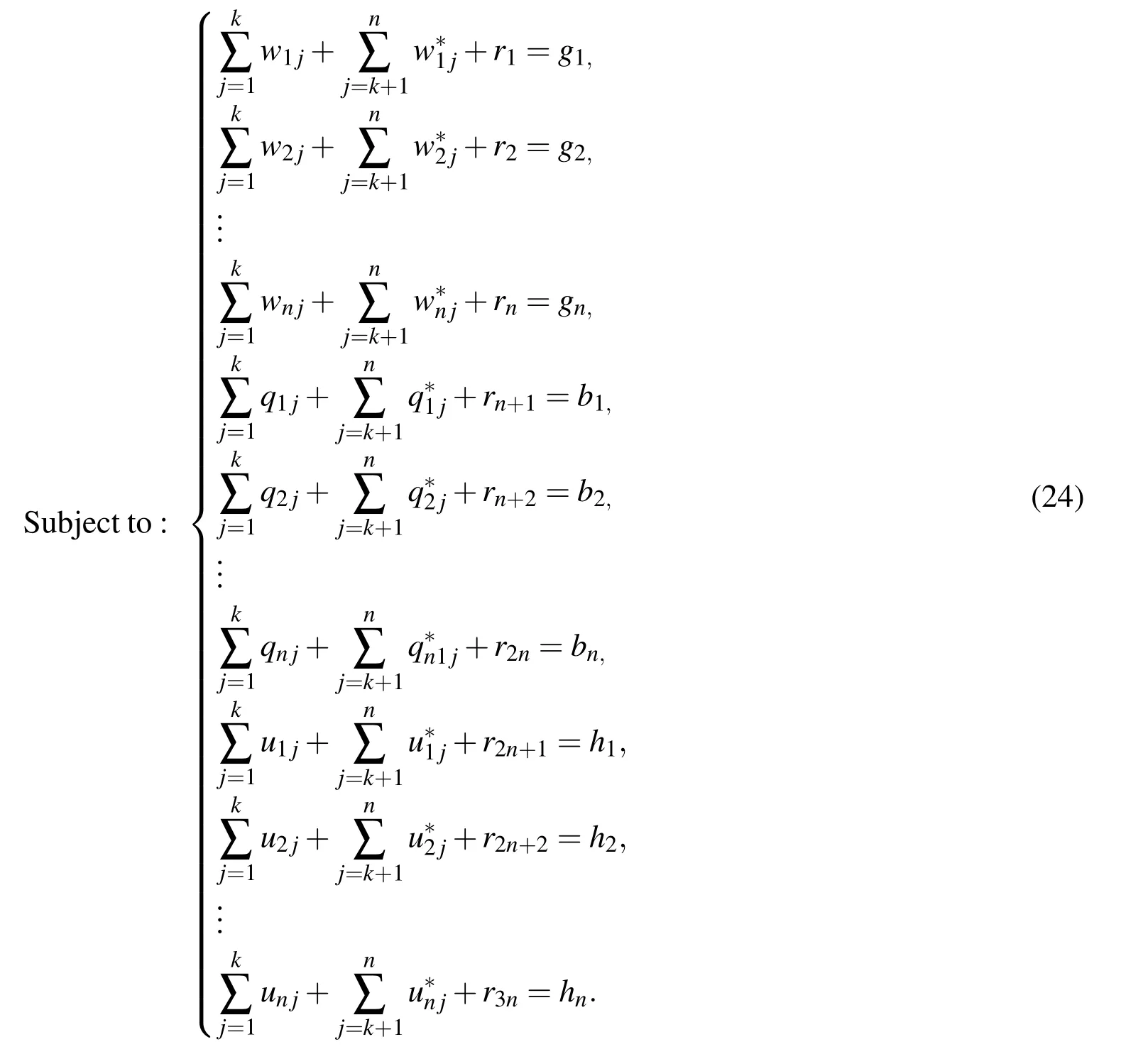
With the non-negative restrictionsandrsfors=1,2,···,n,n+1,···3n≥ 0.Now solving the corresponding LPP(24)one may get the solution accordingly.To illustrate the applicability of the proposed method example problems are solved in the following section.

4 Numerical examples and discussions

Example 1Let us consider a 2×2 fully fuzzy system of linear equations(Otadi and Mosleh 2012)

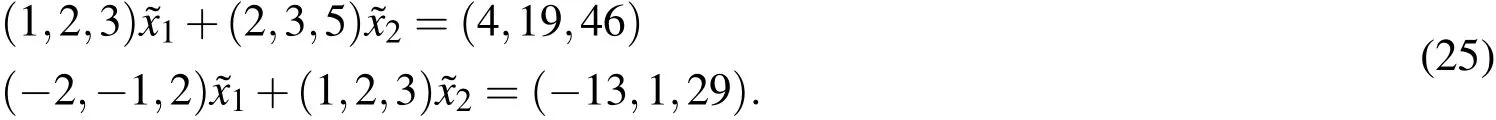
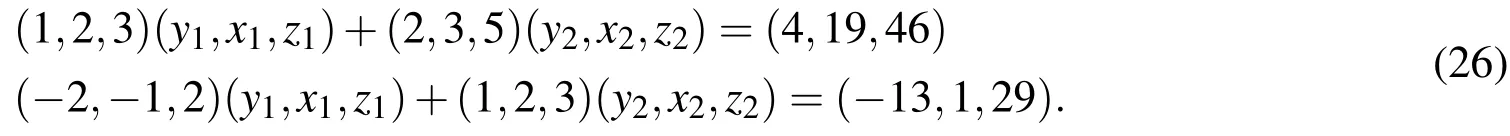
To find the core solution of the above system we have

Solving Eq.(27)we havex1=5 andx2=3.This means all the elements of the solution vector are non-negative.Hence as per the discussion of Case 1,one may have the following system

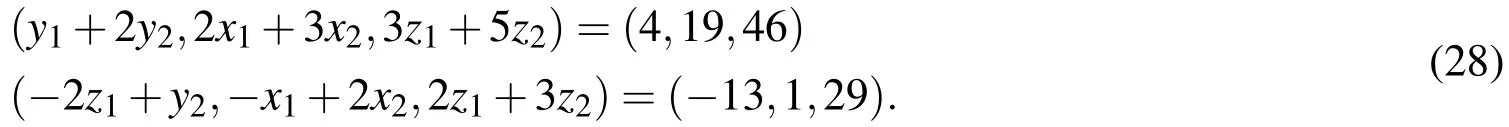
Eq.(28)is equivalently written as

As such,the corresponding linear programming of the above system can be expressed as

Minimize:r1+r2+r3+r4+r5+r6

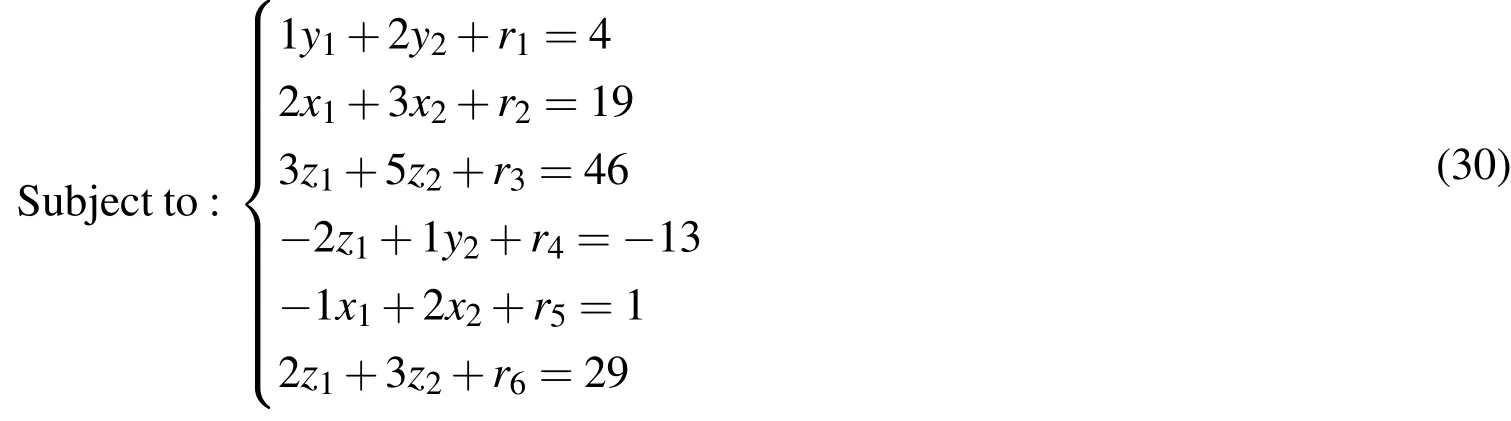
wherer1,r2,···r3n,y1,x1,z1,y2,x2,z2≥ 0.Solving the LPP(30)the optimal solution may be obtained asy1=2,x1=5,z1=7,y2=1,x2=3 andz2=5.Therefore the required fuzzy solution is=(2,5,7)and=(1,3,5).Obtained results are compared with the solution of Otadi and Mosleh(2012)and found that the results are exactly same.

Example 2Next consider a 2×2 fully fuzzy system of linear equations

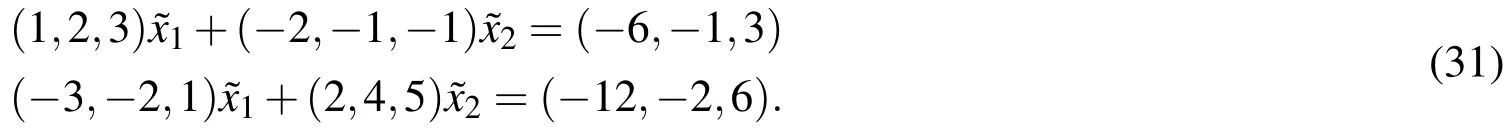
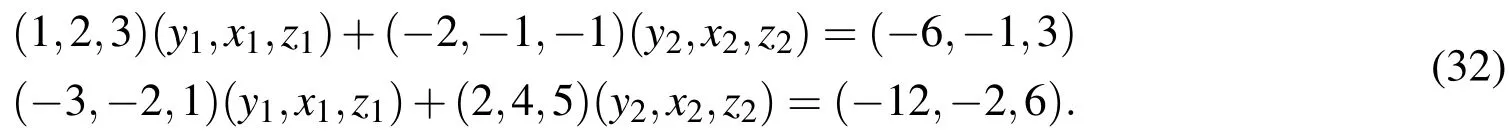
The core solution of the above system can be obtained asx1=-1 andx2=-1.From this we may conclude that the elements of the fuzzy solution vector are non positive.As per the discussion of Case 2 the above system is now expressed by converting the non-positive elements to non-negative elements of the solution as

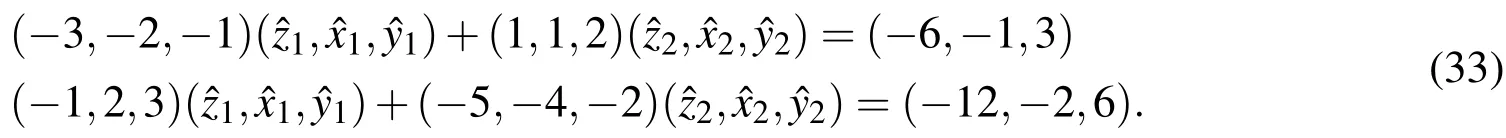
So Eq.(33)may be written as

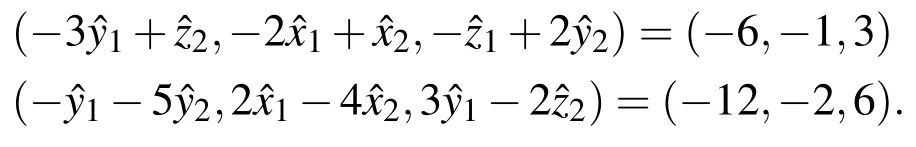
This is equivalent to

Corresponding linear programming of the above system can be expressed as

Minimizer1+r2+r3+r4+r5+r6

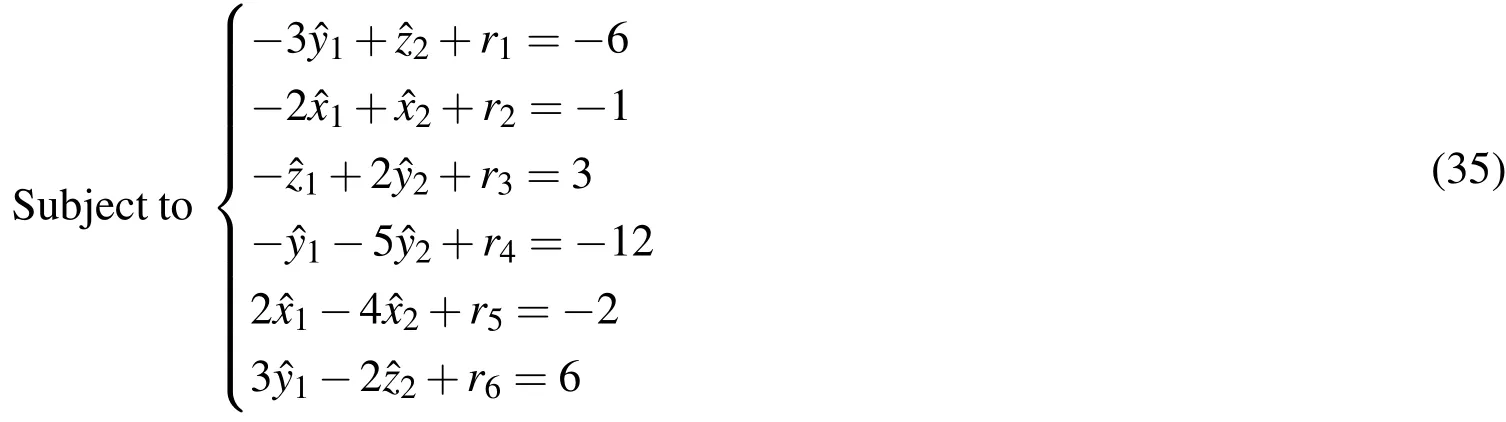
Therefore the required fuzzy solution

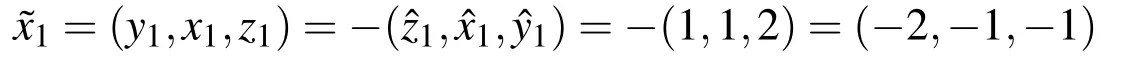
and

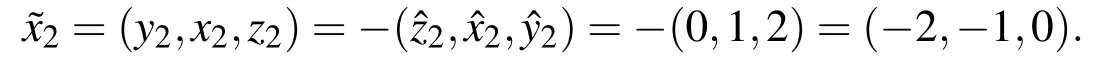
Example 3In this example again let us consider a 2×2 fully fuzzy system of linear equations

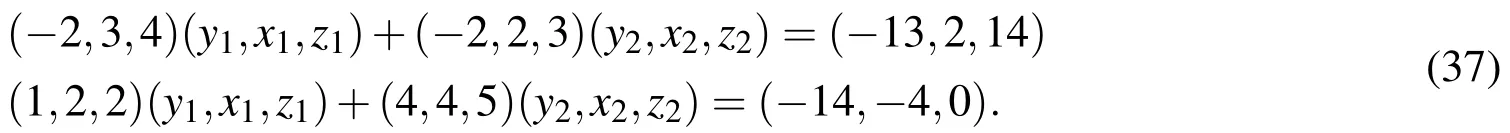
Similarly for the above cases we have the core solution for the above system isx1=2 andx2=-2.So from this we may get that the first and second elements of the fuzzy solution vector are non-negative and non-positive respectively.As per the discussion of Case 3 the above system is now expressed by converting the non-positive element to non-negative as

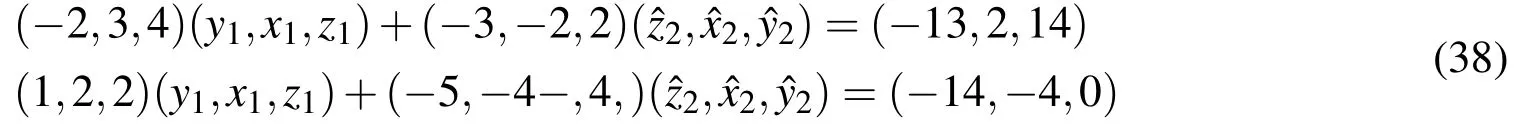
Applying the general rule of fuzzy multiplication and addition we have

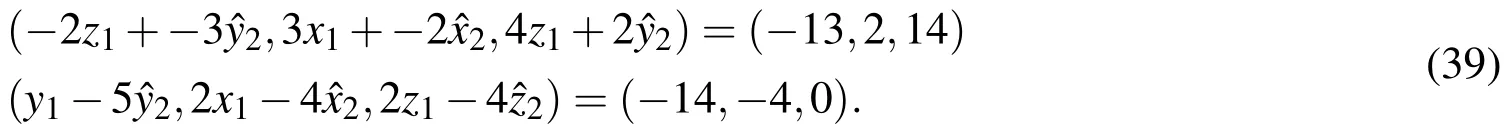
This is equivalent to

The corresponding linear programming of the above system can be expressed as

Minimizer1+r2+r3+r4+r5+r6

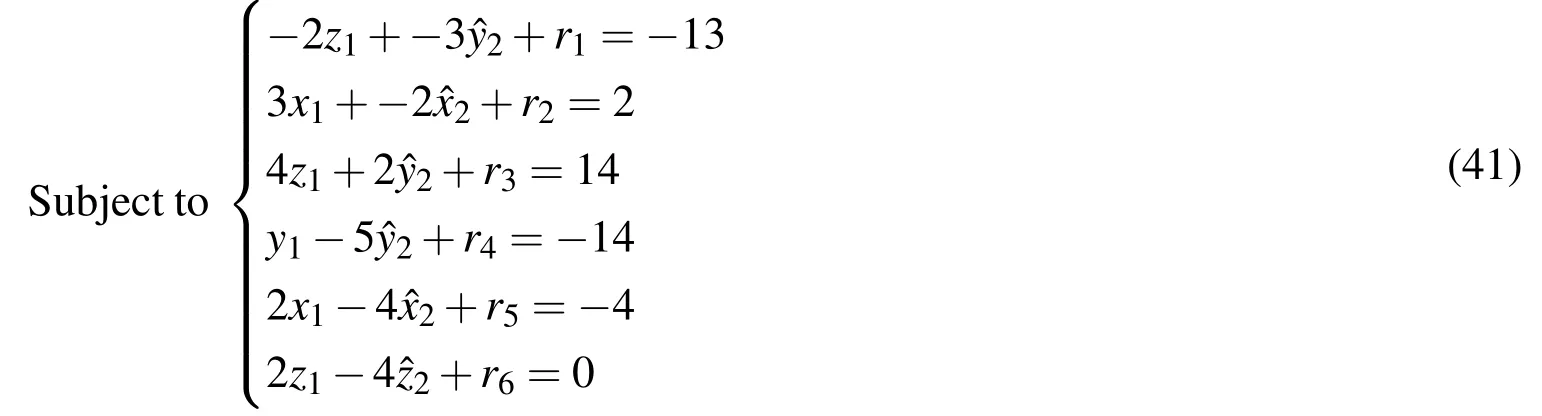
Therefore the required fuzzy solution

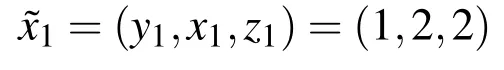
and

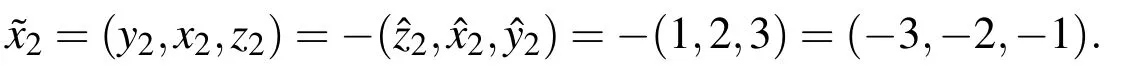
5 Conclusions

This paper uses arithmetic operations on fuzzy numbers and the concept of linear programming for the solution of fully fuzzy system of linear equations.There is no restriction on the coefficient matrix of the corresponding system. The method found efficient when the elements of the fuzzy solution vector are only non-negative,nonpositive or both.Suitable numerical examples are solved to show the efficiency of the proposed method.Results obtained by the proposed method are also compared with the results obtained by the existing methods and found in good agreement.

Abbasbandy,S.;Jafarian,A.;Ezzati,R.(2005):Conjugate gradient method for fuzzy symmetric positive-definite system of linear equations.Applied Mathematics and Computation,vol.171,pp.1184–1191.

Abbasbandy,S.;Jafarian,A.(2006):Steepest descent method for system of fuzzy linear equations.Applied Mathematics and Computation,vol.175,pp.823–833.

Allahviranloo,T.;Hosseinzadeh,A.A.;Ghanbari,M.;Haghi,E.;Nuraei,R.(2014):On the new solutions for a fully fuzzy linear system.Soft Computing,vol.18,pp.95–107.

Allahviranloo,T.;Mikaeilvand,N.(2011):Non-zero solutions of the fully fuzzy linear systems.Applied and Computational Mathematics,vol.10,pp.271–282.

Allahviranloo,T.;Salahshour,S.;Khezerloo,M.(2011):Maximal and minimal symmetric solutions of fully fuzzy linear systems.Journal of Computational and Applied Mathematics,vol.235,pp.4652–4662.

Allahviranloo,T.(2004):Successive overrelaxation iterative method for fuzzy system of linear equations.Applied Mathematics and Computation,vol.162,pp.189–196.

Allahviranloo,T.(2005):The adomian decomposition method for fuzzy system of linear equations.Applied Mathematics and Computation,vol.163,pp.553–563.

Babbar,N.;Kumar,A.;Bansal,A.(2013):Solving fully fuzzy linear system with arbitrary triangular fuzzy numbers.Soft Computing,vol.17,pp.691–702.

Behera,D.;Chakraverty,S.(2012a):A new method for solving real and complex fuzzy system of linear equations.Computational Mathematics and Modeling,vol.23,pp.507–518.

Behera,D.;Chakraverty,S.(2013a):Fuzzy analysis of structures with imprecisely defined properties.Computer Modeling in Engineering and Sciences,vol.96,pp.317–337.

Behera,D.;Chakraverty,S.(2013b):Fuzzy finite element analysis of imprecisely defined structures.Engineering Applications of artificial Intelligence,vol.26,pp.2458–2466.

Behera,D.;Chakraverty,S.(2015):New approach to solve fully fuzzy system of linear equations using single and double parametric form of fuzzy numbers.Sadhana,vol.40,pp.35–49.

Behera,D.;Chakraverty,S.(2013c):Solution method for fuzzy system of linear equations with crisp coefficients.Fuzzy Information and Engineering,vol.5,pp.205–219.

Behera,D.;Chakraverty,S.(2012b):Solution of fuzzy system of linear equations with polynomial parametric form.Application and Applied Mathematics:An International Journal(AAM),vol.7,pp.648–657.

Behera,D.;Chakraverty,S.(2014):Solving fuzzy complex system of linear equations.Information Sciences,vol.277,pp.154–162.

Chakraverty,S.;Behera,D.(2013):Fuzzy system of linear equations with crisp coefficients.Journal of Intelligent and Fuzzy Systems,vol.25,pp.201–207.

Das,S.;Chakraverty,S.(2012):Numerical solution of interval and fuzzy system of linear equations.Application and Applied Mathematics:An International Journal(AAM),vol.7,pp.334–356.

Dehghan,M.;and Hashemi,B.(2006):Solution of the fully fuzzy linear systems using the decomposition procedure.Applied Mathematics and Computation,vol.182,pp.1568–1580.

Dehghan,M.;Hashemi,B.;Ghatee,M.(2007):Solution of the fully fuzzy linear systems using iterative techniques.Chaos,Solitons and Fractals,vol.34,pp.316–336.

DeMarr,R.(1972):Nonnegative matrices with nonnegative inverses.Proceeding of the American Mathematical Society,vol.35,pp.307–308.

Dubois,D.;Prade,H.(1980):Fuzzy sets and systems:Theory and applications.New York,Academic Press.

Fatullayev,A.G.;Koroglu,C.(2012):Numerical solving of a boundary value problem for fuzzy differential equations.Computer Modeling in Engineering and Sciences,vol.86,pp.39–52.

Friedman,M.;Ming,M.;Kandel,A.(1998):Fuzzy linear systems,Fuzzy Sets and Systems,vol.96,pp.201–209.

Gong,Z.;Guo,X.(2011):Inconsistent fuzzy matrix equations and its fuzzy least squares solutions,vol.35,pp.1456–1469.

Gong,Z.;Guo,X.;Liu,K.(2014):Approximate solution of dual fuzzy matrix equations.Information Sciences,vol.266,pp.112–133.

Hanss,M.(2005):Applied Fuzzy Arithmetic:An Introduction with Engineering Applications.Berlin,Springer-Verlag.

Kaufmann,A.;Gupta,M.M.(1985):Introduction to Fuzzy Arithmetic:Theory and Applications.New York,Van Nostrand Reinhold Company.

Muzzioli,S.;Reynaerts,H.(2007):The solution of fuzzy linear systems by nonlinear programming:a financial application.European Journal of Operational Research,vol.177,pp.1218–1231.

Otadi,M.;Mosleh,M.(2012):Solving fully fuzzy matrix equations.Applied Mathematical Modelling,vol.36,pp.6114–6121.

Ross,T.J.(2004):Fuzzy Logic with Engineering Applications.New York,John Wiley and Sons.

Senthilkumar,P.;Rajendran,G.(2011):New approach to solve symmetric fully fuzzy linear systems.Sadhana,vol.36,pp.933–940.

Sun,X.;Guo,S.(2009):Solution to general fuzzy linear system and its necessary and sufficient condition.Fuzzy Information and Engineering,vol.3,pp.317–327.

Yang,Z.;Li,K.;Cai,Q.(2013):Universal reliability method for structural models with both random and fuzzy variables.Computer Modeling in Engineering and Sciences,vol.95,pp.143–171.

Yin,J.F.;Wang,K.(2009):Splitting iterative methods for fuzzy system of linear equations.Computational Mathematics and Modeling,vol.20,pp.326–335.

Zadeh,L.A.(1965):Fuzzy sets.Information Control,vol.8,pp.338–353.

Zimmermann,H.J.(2001):Fuzzy set theory and its application.Boston/Dordrecht/London,Kluwer Academic Publishers.

1Institute of Reliability Engineering,School of Mechatronics Engineering,University of Electronic Science and Technology of China,No.2006,Xiyuan Avenue,West Hi-Tech Zone,Chengdu,Sichuan 611731,P.R.China

2Corresponding author.E-mail:diptiranjanb@gmail.com,diptiranjanb@uestc.edu.cn

3Department of Mathematics,National Institute of Technology Rourkela,Odisha-769008,India