基于迭代散射算法的柱体阵列散射场分析

刘起坤 周东方 邢 锋 雷 雪 余道杰

柱状物体是空间电磁环境中最常见的障碍物，如微波器件内的金属支节、天线支撑架、金属网架天线罩或微波辐照物等，故柱体散射问题一直是国内外的热门研究课题。现有研究柱体散射的方法有很多[15]-，目的是希望获得柱状物体散射场的精确快速分析。其中，迭代算法因为能够对物体之间的多次散射进行精确近似，受到越来越多的关注。现有电磁分析中的迭代算法一般可以分为两类，第 1类是基于传输线理论中的网络思想，建立表征入射波与散射波关系的广义T矩阵，并对T矩阵进行递推实现问题求解[611]-，该类方法一般称为递推T矩阵法；第2类是将原始问题等效为多次散射的叠加，

2015-01-29收到，2015-05-06改回，2015-06-26网络优先出版

国家自然科学基金（62101056）和国家863计划项目（2014AA01A707）资助课题

*通信作者：刘起坤 ed-liuqikun@163.com建立迭代前后散射场之间的关系式，叠加每次迭代时的散射场，得到散射问题的解[12,13]，此种方法一般称为迭代散射法（ISP）。迭代散射法能够快速分析柱体阵列的散射特性，已经应用到腔体内金属枝节或开放空间柱体散射[1416]-等。但是现有文献中ISP算法的物理迭代过程缺乏细致的描述，缺少迭代次数、适用条件等算法的收敛性分析，并且没有给出迭代过程的物理意义。本文对自由空间中细长金属柱体的电磁散射问题进行分析，将初始的场关系展开为Bessel函数或Hankel函数关系式，详细阐述了柱体阵列散射场的迭代过程；根据迭代后散射场的衰减规律，得到ISP算法的最优迭代次数，最后叠加得到柱体阵列的散射场。

2 初始平面波入射

2.1 柱体散射场分析

图1 无限长柱体在坐标系中的位置

如图1建立无限长金属柱体的柱坐标系，柱体i（i表示柱体编号）位于全局坐标系的（dio,φio）位置，观察点P1相对于柱体i局部坐标系的位置为（ρi, φi） ，平面波从-x方向水平入射到柱体i，电场方向与+z方向平行。

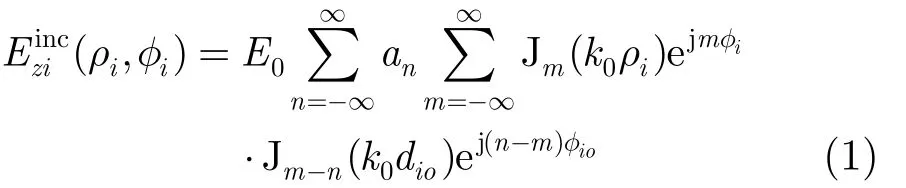
柱体上产生的散射场为向外传播的柱面波，考虑到远场区域散射场为有限值，故散射场可以展开为第2类Hankel函数形式：

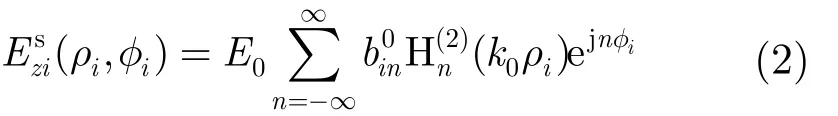
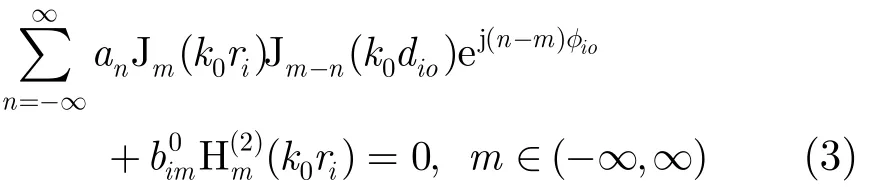
令m取最大值M, n取最大值N，可以推出未迭代时散射场系数 bi0m：

2.2 散射矩阵推导

其中，各矩阵意义如下： [bi0m]表示未迭代时散射场系数矩阵，[Gmi]表示边界条件矩阵，[Tmion]表示柱体i从全局坐标系到局部坐标系的转换关系矩阵，[an]

表示入射场系数矩阵。

3 迭代散射理论

迭代散射的原理是将其余柱体的第 1n- 次迭代后产生的散射场，作为某柱体第n次迭代时的入射场。所以迭代散射的过程，即是分析柱体间相互作用的过程。柱体阵列的间距通常不能满足远场条件，对于长度远大于波长的柱体，散射场可以展开为若干柱面波之和。下面对迭代过程进行详细阐述。

3.1 第1次迭代过程

柱体阵列的模型如图2所示，假设柱体总数为I，取（除去第 i个柱体外的）其余柱体的散射场作为第i个柱体的入射场。

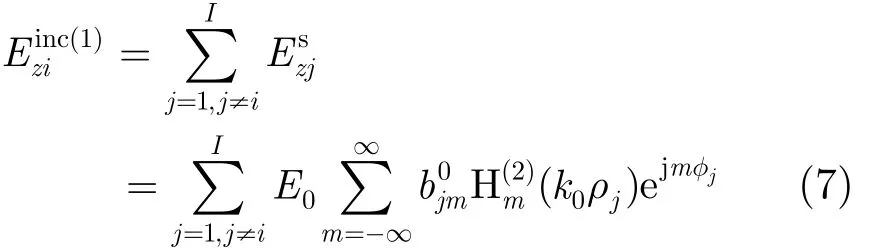
图2 柱体阵列分布模型

第1次迭代时，柱体j（）ji≠局部坐标系下入射场表示为为了计算方便，将各柱体的入射场转换到柱体 i所在局部坐标系下，即

第1次迭代后，柱体i的散射场：

根据理想导体表面边界条件，最终确定第1次迭代后的散射场系数1ipb：

3.2 多次迭代过程

迭代过程同上，可以得出迭代v次后的散射场系数vipb ：

通过多次迭代散射，可以建立散射场系数与入射场系数的相对关系： bV= T （ T （ … T （ a0））） 。

将迭代V次后散射场变换到全局坐标系：

4 迭代散射结果分析

4.1 算法收敛性分析

迭代散射算法基于柱面波函数展开进行分析，限于Bessel函数及Hankel函数的性质，迭代散射算法需要满足一定的近似条件。柱体表面的入射电场近似展开为Bessel函数形式，要求入射电场展开前后的计算误差满足

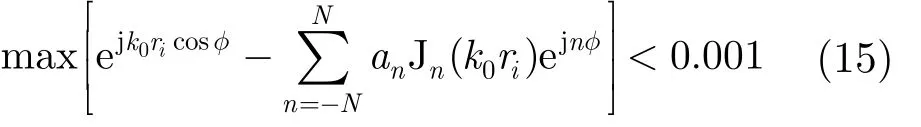
同时，柱体阵列间距有限，迭代的散射场按照Hankel函数展开为若干柱面波之和。由于 Hankel函数在零点位置的数值为奇异点，当柱体间距很小时，迭代的散射场会出现不可预期的畸变。

为了保证算法的有效性，迭代散射算法需要满足以下近似：柱体半径需要满足 ri≤0.5λ，柱体间距dij≥λ，柱面波函数的展开级数N≥ 1 00。

4.2 迭代次数分析

迭代散射的过程可以认为是柱体间相互作用的过程。从理论上说，迭代次数应该无穷多，这显然是不能够实现的。本文对柱体阵列的散射场迭代次数进行分析，确定最优的迭代次数。为了体现计算方法的通用性，选取不同半径、空间位置分布的 4个理想金属柱体C1～C4，如图3所示。仿真频率设为1 GHz，柱体长度为20倍波长，迭代次数为3，柱体半径及相对位置关系见表1。

图3 柱体阵列模型示意图

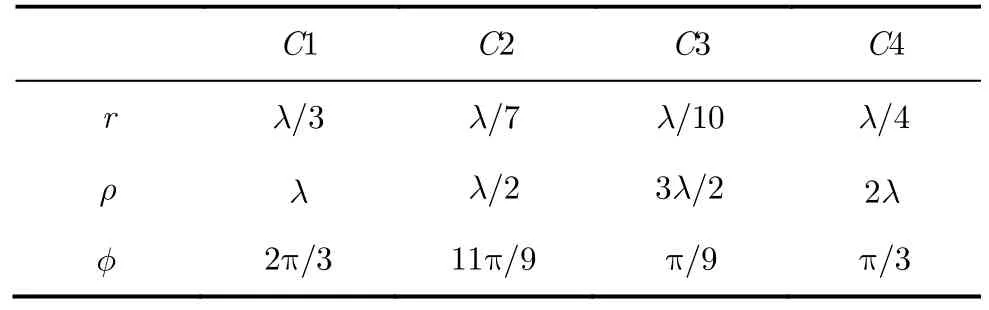
表1 柱体阵列的半径及相对位置数据

为了兼顾计算精度与计算速度，需要确定 ISP算法的迭代次数。本文分别选取图3所示的两个柱体C1和C2, 4个柱体C1～C4，采用迭代散射法对这两组柱体阵列的散射场进行分析，结果如图 4，图5所示。

图4为仅存在柱体C1, C2时，不同迭代次数下柱体C1产生的归一化散射场方向图。从图4中可以看出，未迭代时（图4中迭代0次曲线）柱体在180°方向产生前向主辐射场，这是由于初始入射场从0°方向入射，在180°方向产生较强的前向辐射场。同时，从图中可以看出，迭代次数增加1次，散射场幅度衰减约-15 dB，第3次迭代产生的散射场相对于初始散射场衰减约-50 dB，所以迭代次数取3次即可保证ISP算法的计算精度。

图4 柱体C1局部散射场的迭代分析（柱体C1,C2）

图5 为4个柱体C1～C4的散射场迭代曲线。从迭代曲线来看，未迭代时散射场最大，随着迭代次数增加，散射场的幅值逐渐减小，说明多次迭代后柱体间影响逐渐减小。对比图4，图5可以看出，随着柱体数目的增加，柱体之间的相对关系较为复杂，迭代后散射场不均匀。整体上看，迭代次数增加1次，散射场衰减幅度约-10 dB，第3次迭代产生的散射场比初始散射场衰减约-45 dB，迭代次数取3次即可保证ISP算法的计算精度。

综合来看，迭代次数取3次时，ISP算法分析柱体阵列的散射场可以保证良好的计算精度。

4.3 算法准确度验证

平面波从-x方向照射到柱体阵列上，电场极化方向为+z方向。为了验证ISP算法的准确度，采用电磁仿真软件FEKO Suite 5.5中的矩量法（MoM）模块，对图3所示柱体阵列模型进行对比计算。ISP算法迭代次数为3，仿真频率设为1 GHz，柱体长度为20倍波长，M=100；矩量法模块中设置三角形边长λ/6、线段长度λ/15、线段半径λ/100，两种算法的计算结果如图6所示。

图6为柱体C1产生的总辐射场方向图，以及采用ISP和MoM两种方法计算柱体阵列辐射场的对比曲线，其中图 6（a）为 2个柱体（C1,C2）在 xoy平面的电场方向图，图 6 （b）为 4 个柱体（C1～C4）在xoy平面的电场方向图。从图中可以看出，单个柱体C1在入射波方向（角度0°）产生最大散射；柱体数目增加到2个时，主辐射方向（角度180°）总散射场增加约0.7 dB, 4个柱体时主辐射方向总散射场增加约1 dB。随着柱体数量的增加，散射场的不均匀性逐渐出现，旁瓣电平逐渐增大。对比 MoM 与 ISP的曲线来看，两条曲线的计算结果有着很好的一致性。而计算速度方面，计算4个柱体时MoM计算时间需要3384 s（不含搭建模型时间），而ISP算法计算时间仅需440 s。

5 结论

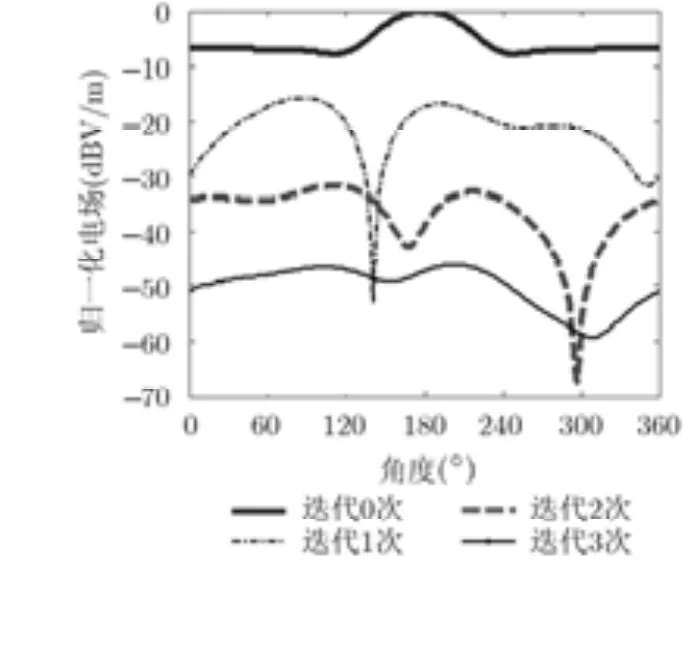
图5 柱体C1的散射场迭代分析（柱体C1～C4）

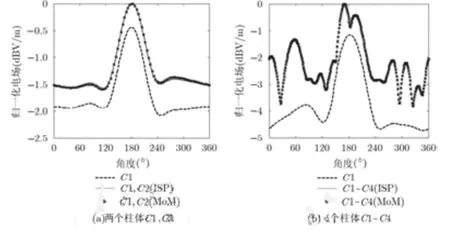
图6 柱体阵列的总场分析

本文采用了迭代散射法分析了阵列的散射场。通过对单个柱体的散射场进行柱面波函数展开，推导出散射场与入射场系数之间的迭代关系。在此基础上，通过分析不同迭代次数下柱体的散射场，在保证计算精度与速度条件下，确定ISP算法的最优迭代次数。在算法精度方面，ISP算法与MoM计算结果吻合良好；在算法速度方面，ISP算法因为无需对柱体进行剖分，计算速度明显优于MoM。本算法不限于柱体阵列散射计算，同样适用于其它柱状物体的散射问题。

[1] 程志华, 谢拥军, 樊君. 复杂目标的太赫兹波近场 RCS快速计算[J]. 电子与信息学报, 2014, 36（8）: 1999-2004.Cheng Zhi-hua, Xie Yong-jun, and Fan Jun. Fast computation of near field RCS of complex objects in terahertz band[J]. Journal of Electronics & Information Technology, 2014, 36（8）: 1999-2004.

[2] 李晓峰, 谢拥军, 杨锐. 半空间电大导体目标散射的高频分析方法[J]. 电子与信息学报, 2009, 31（5）: 1268-1270.Li Xiao-feng, Xie Yong-jun, and Yang Rui. High-frequency analysis on scattering from conductive targets with electrically large size in half space[J]. Journal of Electronics &Information Technology, 2009, 31（5）: 1268-1270.

[3] Nasr M A, Eshrah I A, and Hashish E A. Electromagnetic scattering from a buried cylinder using a multiple reflection approach: TM case[J]. IEEE Transactions on Antennas and Propagation, 2014, 62（5）: 2702-2707.

[4] Wu Xiao-po, Shi Jia-ming, and Wang Jia-chun. Multiple scattering by parallel plasma cylinders[J]. IEEE Transactions on Plasma Science, 2014, 42（1）: 13-19.

[5] 张会云, 刘蒙, 尹贻恒, 等. 基于格林函数法研究金属线栅在太赫兹波段的散射特性[J]. 物理学报, 2013, 62（19）: 240-245.Zhang Hui-yun, Liu Meng, Yin Yi-heng, et al.. Study on scattering properties of the metal wire gating in a THz band based on ‘Green function method’[J]. Acta Phasica Sinica,2013, 62（19）: 240-245.

[6] Kim K T and Kramer B A. Direct determination of the T-matrix from a mom impedance matrix computed using the Rao-Wilton-Glisson basis function[J]. IEEE Transactions on Antennas and Propagation, 2013, 61（10）: 5324-5327.

[7] Behnam Ghassemiparvin and Ayhan Altintas. Scattering from an impedance object at the edge of a perfectly conducting wedge[J]. IEEE Transactions on Antennas and Propagation, 2014, 62（2）: 852-861.

[8] Ye Xiu-zhu, Chen Xu-dong, Yu Zhong, et al.. Simultaneous reconstruction of dielectric and perfectly conducting stutterers via T-matrix method[J]. IEEE Transactions on Antennas and Propagation, 2013, 61（7）: 3774-3781.

[9] Cao Lei, Li Wei, and Hu Jun. A new T-matrix formulation for electromagnetic scattering by a radially multilayered gyroelectric sphere[J]. IEEE Transactions on Antennas and Propagation, 2013, 61（2）: 836-842.

[10] Zhuromskyy O and Peschel U. T-matrix analysis of dipole waves on chains of dielectric particles[C]. 7th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics-Metamaterials, Bordeaux, France,2013: 268-270.

[11] Tsang Leung and Chang Xin. Modeling of vias sharing the same antipad in planar waveguide with boundary integral equation and group T-matrix method[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology,2013, 3（2）: 315-327.

[12] Ozdemir N A, Ovejero D G, and Craeye C. On the relationship between multiple-scattering macro basis functions and Krylov subspace iterative methods[J]. IEEE Transactions on Antennas and Propagation, 2013, 61（4）:2088-2098.

[13] Desmal A and Ba c H. Shrinkage-thresholding enhanced born iterative method for solving 2D inverse electromagnetic scattering problem[J]. IEEE Transactions on Antennas and Propagation, 2014, 62（7）: 3878-3884.

[14] Polewski M, Lech R, and Mazur J. Rigorous modal analysis of structures containing inhomogeneous dielectric cylinders[J].IEEE Transactions on Microwave Theory and Techniques,2004, 52（5）: 1508-1516.

[15] Kusiek A, Kowalczyk P, and Mazur J. Analysis of scattering from arbitrary conflguration of elliptical obstacles using T-matrix representation[J]. IET Microwaves, Antennas &Propagation, 2008, 2（5）: 434-441.

[16] Adam Kusiek, Rafal Lech, and Jerzy Mazur. A new hybrid method for analysis of scattering from arbitrary conguration of cylindrical objects[J]. IEEE Transactions on Antennas and Propagation, 2008, 56（6）: 1725-1733.