Molecular Dynamics Analysis of High-temperature Molten-salt Electrolytes in Thermal Batteries

C.F.Chen,H.Y.Liand C.W.Hong,2

Molecular Dynamics Analysis of High-temperature Molten-salt Electrolytes in Thermal Batteries

C.F.Chen1,H.Y.Li1and C.W.Hong1,2

The purpose of this research is to improve the discharge rate and to predict the melting point of high-temperature molten-salt electrolytes in thermal batteries.Using molecular dynamics(MD)simulation techniques,we tried to develop some novel ternary and quaternary molten electrolytes to replace conventional binary LiCl–KCl ones.The simulation results with greater ionic conductivity and lower melting point are consistent with experimental results reported by previous literatures.The MD results have found that the lithium ion mole fraction in the molten-salt electrolytes affects the ionic conductivity significantly.This paper demonstrates that MD simulation techniques are a useful tool to screen various design ideas on the multi-component electrolytes in a more efficient way.The molecular composition of each component of the molten-salt electrolytes can be optimized using this atomistic analysis instead of trial-and-error experiments.

Molecular dynamics(MD),Thermal battery,Molten-salt electrolyte,Ionic conductivity,Melting point.

1 Introduction

High-temperature molten-salt batteries(or thermal batteries)are excellent power sources for military applications,and potentially for electric vehicles as well as grid energy storage.They are rugged,robust,reliable with excellent power density,and can be stored without degradation for more than 20 years[Guidotti and Masset(2006);Masset and Guidotti(2007);Masset and Guidotti(2007)].They feature high output power and superior stability in long-time storage,which are especially suitable to emergency applications.Thermal batteries consist of two functional parts:a heat generation system that generates heat and maintains the molten salt in the molten state,and an electrochemical cell system which generates electricpower.Thermal batteries are mainly used as electrical power generators in military equipment,including missiles,guided bombs,shells,decoys,torpedoes,and aircraft security systems[Masset P.(2006);Masset,Schoeffert,Poinso,and Poignet(2005); Ratnakumar,Smart,Kindler,Frank,Ewell,and Surampudi(2003)].Thermal batteries are also applied in civil high-technology appliances,such as satellites,rocket launchers,and specific applications such as geothermal generators[Dagarin,Taenaka,and Stofel(1996);Guidotti,Reinhardt,and Odinek(2004)].

Improving the overall performance of thermal batteries for growing electronic demand is always a target for battery developers.Various methods for increasing the ionic conductivity and lowering the melting point,such as using new electrolytes of ternary and quaternary molten-salt systems,have been proposed to increase the power output.Recently,Fujiwara et al.[Fujiwara,Kato,Watanabe,Inaba,and Tasaka(2009);Fujiwara,Inaba,and Tasaka(2010);Fujiwara,Inaba,and Tasaka(2011);Fujiwara(2012)]developed a new simulation technique using the CALPHAD(Calculation of Phase Diagram and Thermodynamics)method to predict the ionic conductivity and the melting point.They proposed that the target of the ionic conductivity should be over 2.0 Scm−1or higher and the melting point should between a temperature range of 623-703K(350-430˚).Due to the fact that experimental trial-and-errors on high-temperature molten-salt batteries are tedious to conduct,and most experiments cannot observe the detailed process inside the batteries,we need to develop a more efficient simulation technique,in which the chemical and physical properties can be predicted and the ion interactions inside the electrolyte can also be observed.Although Galamba et al.[Galamba,Nieto de Castro,and Ely(2004);Galamba,Nieto de Castro,and Ely(2007)],Ohtori et al.[Ohtori,Oono,and Takase(2009);Ohtori,Salanne,and Madden(2009)],and Salanne et al.[Salanne,Marrocchelli,Merlet,Ohtori,and Madden(2011)]have recently developed the equilibrium and non-equilibrium molecular dynamics techniques for molten salts and have achieved some results,they are limited in simple molten-salt compositions.

This research mainly develops the molecular dynamics technique to simulate the ternary and quaternary electrolytes to replace the conventional binary ones.These molten-salt electrolytes contain neither environmentally unstable anions,such as iodides,nor expensive cations,such as rubidium and cesium.Ionic conductivities and melting temperatures are the two major parameters that influence the performance of these thermal batteries.We use simulation techniques to tune the lithium ion mole fraction(from 0.05 to 0.95)to achieve the greatest ionic conductivity with melting temperature as lower as possible.The following sections will describe the simulation model and those computational results.

2 Simulation model and conditions

This research mainly studies five types of eutectic salts,as displayed in Table 1,used as the electrolytes for the thermal batteries.Their molecular structures are set up in a unit cell with the volume around 50 Å×50 Å×50 Å.The total number of atoms is approximately 8000,comprising 4000 cations(Li+,Na+,and K+)and 4000 anions(Cl−and Br−).Figure 1 shows the molecular structures of the binary LiCl–KCl,ternary LiCl–LiBr–NaCl and LiCl–LiBr–NaBr,as well as quaternary LiCl–LiBr–NaCl–KCl and LiCl–LiBr–NaBr–KBr electrolytes.Their molecular structures were evaluated from their minimized total energies and softsphere models[Haile(1997);Cheng Lee,and Hong(2007)]were adopted.Details of their compositions and simulation conditions are listed in Table 1 and Table 2

Table 1:Various molten-salt electrolytes.

Table 2:Summary of simulation conditions.

This simulation was carried out on a Material Studio 5.5platform,which was developed by Accelrys Corporation to analyze the nanostructure and to predict properties of various materials.A potential function called COMPASS(condensed-phase optimized molecular potential for atomistic simulation study)[Duan,Li,and Zhu(2011);Sun(1998)]was employed to evaluate the potential energy of organic and inorganic materials.Its ab initio force field also enables accurate and simultaneous predictions of the condensed-phase properties(equation of state,cohesive energies,etc.)of a broad range of atoms,molecules,and polymers.The potential equation is expressed as

This force field was parameterized to predict various properties of molecules in an isolated system and in a condensed phase state.Molecular properties include molecular structures,vibrational frequencies,conformation energies,dipole moments,liquid structures,crystal structures,and cohesive energy densities.The parameterization procedure is divided into two phases:ab initio parameterization and semi-empirical optimization.In the first phase,partial charges and valence parameters are derived to fit to the ab initio potential energy surfaces.In the second phase,the force field is semi-empirically fitted to ensure strong agreement with the experimental data.

The simulation procedure can be divided into two stages:equilibration and production.In this study,the simulation was carried out using a fixed number of atoms,fixed volume,and fixed temperature(NVT)ensemble[Darden York,and Pedersen(1993)].The Ewald summation technique[Hoover(1985);Nose(1984)]for evaluating the long-range electrostatic interactions in the Columbic term was employed.Detailed description of this molecular modeling technique has been explained in the textbook[Allen and Tildesley(1987)]and also in our previous papers[Cheng,Chen,and Hong(2008);Lee and Hong(2010);Lee and Hong(2009);San,Chiu and Hong(2011);San and Hong(2011);San and Hong(2012)].

3 Results and discussion

3.1 Diffusion coefficient and ionic conductivity analysis

The mobility of lithium ions can be determined based on a quantitative mean square displacement(MSD),which is defined as

where N is the number of total atoms,rn(t)represents the position vector of atom n at time t,t0is the initial time step,and the brackets hi indicate time averaging.The diffusion coefficient,D,can be evaluated from the slope of the MSD curves versus elapsed time and B is a constant.Figure 2 shows the MSD tendency of the molten salt ions at a fixed temperature.The fixed temperature of LiCl–KCl was set at 723 K,and that of the remaining electrolytes was set at 773 K for experimental verification.All MSD curves exhibited an approximately linear proportion to the elapsed time,indicating that the ions behaved like transport fluids during the simulation and con firming that all salts reached the molten(or liquid)state.This figure also shows that the slope of the LiCl–LiBr–NaBr–KBr(quaternary-2)is the greatest,the LiCl–KCl(binary)is the lowest,which means that quaternary may have higher ionic conductivity than the others.

The ionic conductivity can be determined from the Nernst–Einstein relation,which is expressed by

Figure 2:Mean square displacement(MSD)versus elapsed for different materials of molten-salt electrolytes.

where σ the ionic conductivity,N is the number of lithium ions,e is the charge of mobile ions,Dselfis the self diffusion coefficient of lithium ions,V is the volume of the simulation system,KBis the Boltzmann constant,and T is the operation temperature of the simulation system.Figure 3 shows a comparison of the simulation and experimental ionic conductivities in different molten-salt electrolytes.The simulation results are lower than the experimental data slightly,but the trend is exctly predicted.

Figure 4 shows the ionic conductivities at different operating temperatures for all electrolytes.The ionic conductivity predictions of the binary electrolytes are also compared with experimental results.The simulation and experimental results for LiCl-KCl are highly consistent and the deviations are within 5%–7%.Temperature was found to be the key factor and is directly proportional to the ionic transport.Teneray-2(LiCl–LiBr–NaBr)exhibits the highest ionic conductivity,while quaternary-2(LiCl-LiBr-NaBr-KBr)comes to the second,when the operating temperatures are over 723K.

Figure 3:Simulation and experimental ionic conductivities in different molten-salt electrolytes.Experimental results are from references Masset and Guidotti(2007);Ratnakumar,Smart,Kindler, Frank,Ewell,and Surampudi(2003);Dagarin,Taenaka,and Stofel(1996).

The above results can be converted to the Arrhenius plots as shown in Figure 5.It is for judgement of the dependence of ionic conductivity on the temperature.The chemical activation energy can also be calculated from the log form of the Arrhenius law as below

where σ is the ionic conductivity,T is the opearting temperature,A is the preexponential factor,kBis the Boltzmann constant,and Eais the activation energy.In this study,the operation temperature ranged between 673 K and 873 K.The relationship between log(σ ·T)and the reciprocal temperature(1/T)can be fitted to straight lines in the plots.The value of the extrapolated intercept at y axis is ln(A),and the slope of the straight line equals(-Ea/kB).The activation energy of each electrolyte calculated from the above diagram is shown in Table 3,which indicates that the Tenary-1 has the lowest activation barrier.Figure 5(a)also shows that the linear fit of the simulation results is consistent with the experimental results

Figure 4:Ionic conductivities at different operating temperatures(673,723,773,823,and 873 K)for all five kinds of molten salt electrolytes.*references[Masset and Guidotti(2007)]

Table 3:Activation energies evaluated from simulation conditions.

3.2 Radial distribution function and molecular structure analysis

The radial distribution function(RDF),denoted as g(r),is a parameter for investigating the molecular structure by counting the local number density divided by the total system density.It is employed to predict the conjugation probability between two molecules.The equation for defining the radial distribution function g(r)is

Figure 5:Arrhenius plots of the ionic conductivity versus the reciprocal temperature for(a)Binary,(b)Ternary-1,(c)Ternary-2,(d)Quaternary-1,and(e)Quaternary-2 electrolytes.*references[Masset and Guidotti(2007)]

where hi indicates the time average,N(r,∆r)is the number of atoms within a spherical shell of r+∆r,N is the total number of atoms in the systems,ρ is the system number density,andV(r,∆r)is volume of the shell.

Figure 6 shows the radial distribution function g(r)diagram for lithium-ions,revealing that all electrolytes reached the molten state when the operation temperature is high enough.According to the height of the first peak,the electrolytes are ranked in the following order:Binary LiCl–KCl(g(r)is around 2.022)is much greater than the others,such as Quaternary-1 LiCl–LiBr–NaCl–KCl(g(r)is around 1.715),Tenary-2 LiCl–LiBr–NaBr(g(r)is around 1.701),Tenary-2 LiCl–LiBr–NaCl(g(r)is around 1.699),and Quaternary-2 LiCl–LiBr–NaBr–KBr(g(r)is around 1.692).This trend implies that the lithium-ion pairs of the binary electrolyte aggregate around are stronger than the ternary and quaternary ones.It indicates that the g(r)values increase as the moveability of the lithium ions decreased corresponding to their molecular weights.

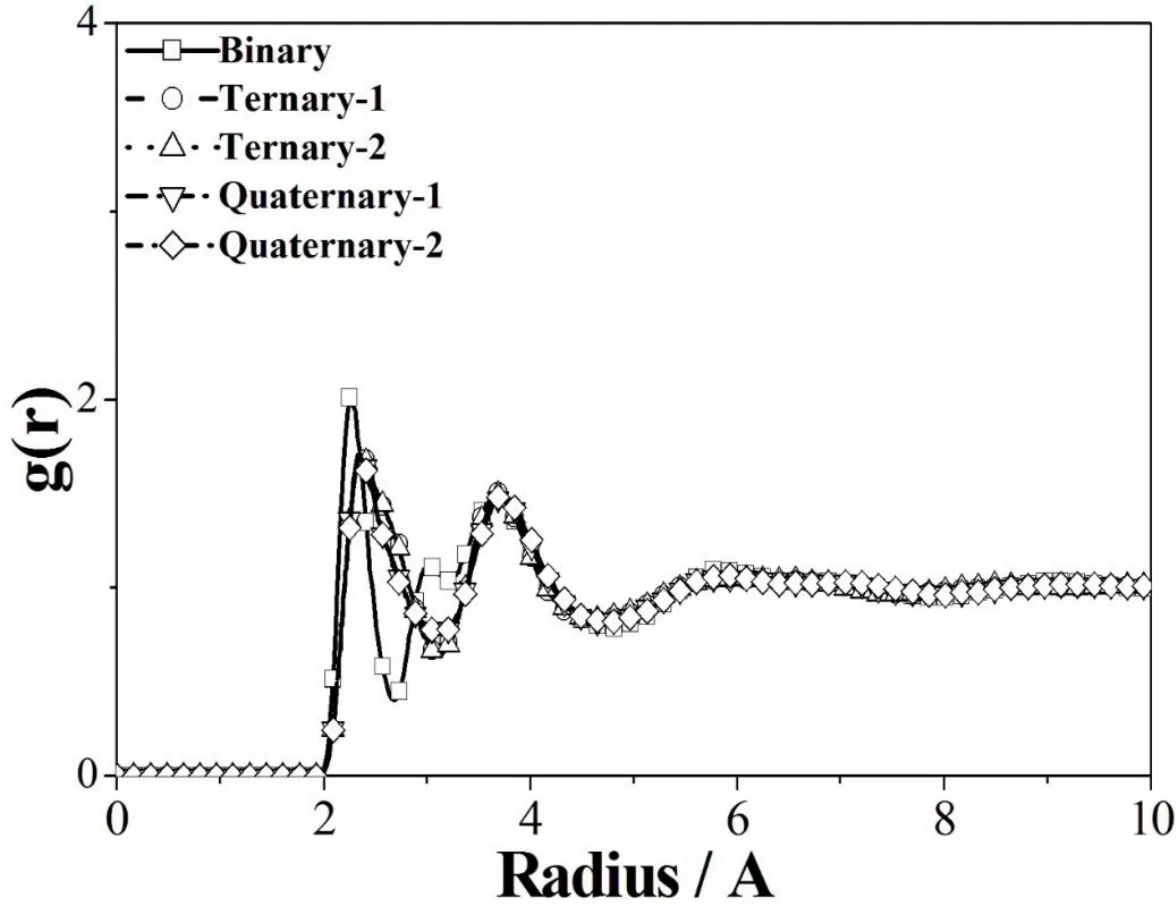
Figure 6:Radial distribution function g(r)of the Li+pair in different molten-salt electrolytes.

3.3 Mole fraction of lithium ions

Effects of the mole fraction of lithium ions in the composition of various electrolytes on the ionic conductivity are worth studying.Figure 7(a)shows the simulation results for the five types of electrolytes when the lithium ion mole fraction varies from 0.05 to 0.95.Comparing with the experimental results reported by Fujiwara et al.,our simulation results are slightly lower than the experimental data as shown in Figure 7(b)for Ternary-1 and Ternary-2 electrolytes.The Quaternary-1 and Quaternary-2 electrolyte results are shown in Figure 7(c)and indicate that approximately 0.6 of lithium ion mole fraction exhibites the maximal ionic conductivity.The overall results of this study suggested that,to obtain the optimal ionic conductivity,the lithium ion mole fraction should be approximately 0.7 for ternary ones and 0.6 for quaternary electrolytes.

3.4 Prediction of the melting point

Melting point plays an important role in thermal batteries as the indication of phase change of the electrolyte from solid to molten state.Using this MD simulation technique,we reversed the process from melting to cooling by setting the operating temperature from 900 K to 300 K,step by step.The phase change from the molten state to the solid state can be identified by an energy jump occurs in the total energy versus temperature diagram as shown in Figure 8.The melting point(energy jump temperature)of the Binary LiCl–KCl is around 615K,Ternary-1(LiCl–LiBr-NaCl)is around 718 K,Ternary-2(LiCl–LiBr–NaBr)is about 739 K,Quaternary-1(LiCl-LiBr–NaCl–KCl)is 688 K,and Quaternary-2(LiCl–LiBr–NaBr–KBr)is at 68 K.They are displayed in Table 4 and show acceptable accuracy by comparison with experimental results.Figure 9 shows that our predictions of Ternary-1 and Ternary-2 are over the experimental results and all the other three electrolytes are below the experimental ones but within the error bars.Although the melting temperatures are not so accurately predicted,the trend of the variation is exactly predicted.The simulated results show that the rank of the melting points:ternary electrolytes are greater than quaternary ones;and quaternary electrolytes are greater than binary ones.

3.5 Target operation region

The target region for tuning the properties of the electrolytes is to achieve that the ionic conductivity over 2.2 Scm−1and the melting point is less than 693 K,which locates in the Zone B in Figure 10.We use letters a,b,c,d,e to represent binary,ternary–1,ternary–2,quaternary–1,and quaternary–2 electrolytes,respectively.Only querternary ones(d and e)are in the target region,hence we can suggest that the Quaternary-1(LiCl-LiBr-NaCl-KCl)and Quaternary-2(LiCl-LiBr-NaBr-KBr)are the best choice.The former has greater ionic conductivity and higher melting point;the latter has slightly lower ionic conductivity but the melting temperature is also lower.All the detailed data are displayed in Table 4.

Figure 7:Ionic conductivities in molten-salt electrolytes versus Li-ions mole fraction for(a)all electrolytes;(b)simulation and experimental results of Ternary-1 and Ternary-2 electrolytes;and(c)simulation and experimental results of Quternary-1 and Quternary-2 electrolytes.

Figure 8:Variation of total energy versus operating temperature for(a)Binary,(b)Ternary-1,(c)Ternary-2,(d)Quaternary-1,and(e)Quaternary-2 electrolytes.The location of the energy jump indicates the phase change.

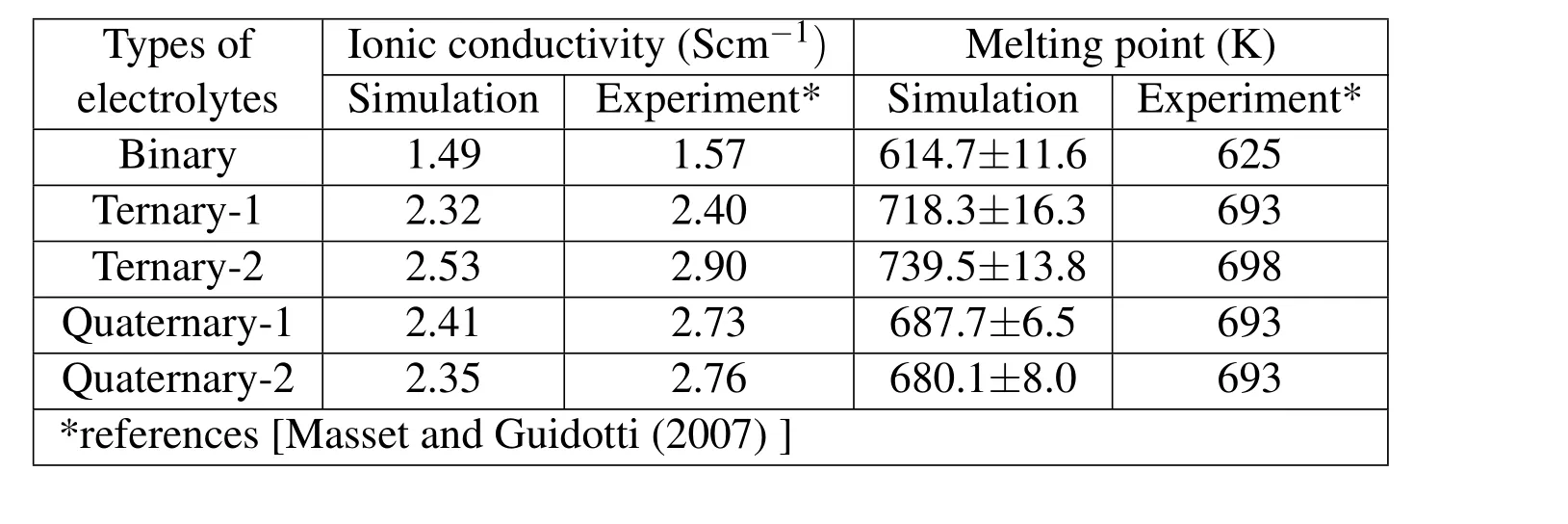
Table 4:Comparison of simulation and experimental results of ionic conductivities and melting points of various electrolytes.

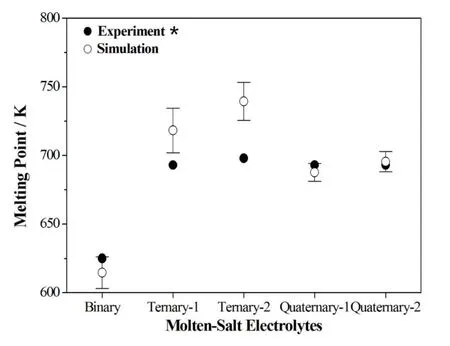
Figure 9:Comparison of simulation and experimental melting points in different molten-salt electrolytes.*references[Masset and Guidotti(2007)Masset,Schoeffert, Poinso,and Poignet(2005);Dagarin,Taenaka,and Stofel(1996)]

Figure 10:The target operating region of the molten electrolytes is at Zone B,where a(Binary)is in Zone C;b(Ternary-1)and c(Ternary-2)are in Zone A;Only d(Quaternary-1)and e(Quaternary-2)electrolytes are qualified.

4 Conclusion

To reduce the tedious work to promote the ionic conductivity and to lower the melting point in the same time for high-temperature molten-salt electrolyte thermal batteries,this research employs the molecular simulation technique to study some novel electrolytes.Our simulation results are within the acceptable accuracy comparing with the results of previous experimental studies regarding the LiCl-LiBr-based ternary(LiCl–LiBr–NaCl&LiCl–LiBr–NaBr)and quaternary(LiCl–LiBr–NaCl–KCl&LiCl–LiBr–NaBr–KBr)electrolytes.The detailed inside results suggested that the lithium ion mole fraction significantly affects the ionic conductivity.It was concluded that the use of novel LiCl–LiBr-based ternary and quaternary molten-salt electrolytes can improve the discharge rate in future thermal batteries because of their greater ionic conductivities and lower melting points than the conventional LiCl–KCl binary one.The quaternary ones can further reduce their melting temperatures for future development.

This molecular simulation technique is a useful tool for evaluating ionic conductivity,predicting melting point,and to understand the interactions between each ions.This paper demonstrates that MD simulation techniques are a useful tool to screen various design ideas on the multi-component electrolytes in a more efficient way.The molecular composition of each component of the molten-salt electrolytes can be optimized using this simulation technique instead of trial-and-error experiments.Our academic future work is to develop the first-principles molecular dynamics technique to replace the current semi-empirical potential functions.

Acknowledgement:We thank the National Science Council of Taiwan and the National Chung-Shan Institute of Science and Technology for their support under the grant numbers NSC 102-2623-E-007-002-D.We are also grateful to the National Center for High-Performance Computing for the facilities made available to us.

Allen,M.P.;Tildesley,D.J.(1987):Computer Simulation of Liquids.Oxford University Press,New York.

Cheng,C.H.;Chen,P.Y.;Hong,C.W.(2008):Atomistic analysis of hydration and thermal effects on proton dynamics in the Nafion membrane.J.Electrochem.Soc.,vol.155,pp.435-442.

Cheng,C.H.;Lee,S.F.;Hong,C.W(2007):Ionic Dynamics of an Intermediate-Temperature Yttria-Doped-Ceria Electrolyte.J.Electrochem.Soc.,vol.154,pp.158-163.

Dagarin,B.P.;Taenaka,R.K.;Stofel,E.J.(1996):Galileo Probe Battery System.IEEE Aerosp.Electron.Syst.Mag.,vol.11,pp.6-13.

Darden,T.;York,D.;Pedersen,L.(1993):Particle mesh Ewald an N·log(N)method for Ewald sums in large systems.J.Chem.Phys.,vol.98,pp.89-92.

Duan,X.H.;Li,J.F.;Zhu,W.J.(2011):Molecular Dynamics Simulation of Ionic Transport on Molten Li–KCl Interface.Inter.J.Quan.Chem.,vol.111,pp.3873-3880.

Fujiwara,S.;Kato,F.;Watanabe,S.;Inaba,M.;Tasaka,A.(2009):New iodide-based molten salt systems for high temperature molten salt batteries.J.Power Sources,vol.194,pp.1180-1183.

Fujiwara,S.;Inaba,M.;Tasaka,A.(2010):New molten salt systems for hightemperature molten salt batteries:LiF–LiCl–LiBr-based quaternary systems.J.Power Sources,vol.195,pp.7691-7700.

Fujiwara,S.;Inaba,M.;Tasaka,A.(2011):New molten salt systems for high temperature molten salt batteries: Ternary and quaternary molten salt systems based on LiF–LiCl,LiF–LiBr,and LiCl–LiBr.J.Power Sources,vol.196,pp.4012-4018.

Fujiwara,S.(2012):Molten salt and thermal battery.U.S.Patent,US008221912B2.

Galamba,N.;Nieto de Castro,C.A.;Ely,J.F.(2004):Thermal conductivity of molten alkali halides from equilibrium molecular dynamics simulations.J.Chem.Phys.,vol.120,pp.8676-8682.

Galamba,N.;Nieto de Castro,C.A.;Ely,J.F.(2007):Equilibrium and nonequilibrium molecular dynamics simulations of the thermal conductivity of molten alkali halides.J.Chem.Phys.,vol.126,pp.204511.

Guidotti,R.A.;Reinhardt,F.W.;Odinek,J.(2004):Overview of high-temperature batteries for geothermal and oil/gas borehole power sources.J.Power Sources,vol.136,pp.257-262.

Guidotti,R.A.;Masset,P.(2006):Thermally activated(thermal)battery technology Part I.An overview.J.Power Sources,vol.161,pp.1443-1449.

Haile,J.M.(1997):Molecular Dynamics Simulation:Elementary Methods,John Wiley&Sons,New York.

Hoover,W.G.(1985):Canonical dynamics Equilibrium phase-space distributions.Phys.Rev.A,vol.31,pp.1695-1697.

Lee,S.F.;Hong,C.W.(2010):Multi-scale design simulation of a novel intermediate temperature micro solid oxide fuel cell stack system.Int.J.of Hydrogen Energy,vol 35,pp.1330-1338.

Lee,S.F.;Hong,C.W.(2009):Computer modeling of ionic conductivity in low temperature doped ceria solid electrolytes.CMC-Computers,Materials&Continua,vol.12,no.3,pp.223235.

Masset,P.;Guidotti,R.A.(2007):Thermally activated(thermal)battery technology Part II.Molten salt electrolyte.J.Power Sources,vol.164,pp.397-414.

Masset,P.;Henry,A.;Poinso,J.-Y.;Poignet,J.-C.(2006):Ionic conductivity measurements of molten iodide-based electrolytes.J.Power Sources,vol.160,pp.752-757.

Masset,P.(2006):Iodide-based electrolytes:A promising alternative for thermal batteries.J.Power Sources,vol.160,pp.688-697.

Masset,P.;Schoeffert,S.;Poinso,J.-Y.;Poignet,J.-C.(2005):LiF-LiCl-LiI vs.LiF-LiBr-KBr as Molten Salt Electrolyte in Thermal Batteries.J.Electrochem.Soc.,vol.152,pp.A405-A410.

Nose,S.(1984):A unified formulation of the constant temperature molecular dynamics methods.J.Chem.Phys.,vol.81,pp.511-.519.

Ohtori,N.;Oono,T.;Takase,K.(2009):Thermal conductivity of molten alkali halides:Temperature and density dependence.J.Chem.Phys.,vol.130,pp.44505.

Ohtori,N.;Salanne,M.;Madden,P.A.(2009):Calculations of the thermal conductivities of ionic materials by simulation with polarizable interaction potentials.J.Chem.Phys.,vol.130,pp.104507.

Ratnakumar,B.V.;Smart,M.C.;Kindler,A.;Frank,H.;Ewell,R.;Surampudi S.(2003):Lithium batteries for aerospace applications:2003 Mars Exploration Rover.J.Power Sources,vol.119,pp.906-910.

Salanne,M.;Marrocchelli,D.;Merlet,C.;Ohtori,N.;Madden,P.A.(2011):Thermal conductivity of ionic systems from equilibrium molecular dynamics.J Phys.Condensed Matter,vol.23,pp.102101.

San,C.H.;Chiu,C.P.;Hong,C.W.(2011):First principles computations of the oxygen reduction reaction on solid metal clusters.CMC-Computers,Materials&Continua,vol.26,no.3,pp.167-186.

San,C.H.;Hong,C.W.(2011):Molecular design of the solid copolymer electrolytepoly(styrene-b-ethylene oxide)for lithium ion batteries.CMC-Computers,Materials&Continua,vol.23,no.2,pp.101-117.

San,C.H.;Hong,C.W.(2012):Quantum analysis on the platinum/nitrogen doped carbon nanotubes for the oxygen reduction reaction at the air cathode of lithium-air batteries and fuel cells.J.Electrochem.Soc.,vol.159,pp.116121.

Sun,H.(1998):COMPASS:An ab Initio Force-Field Optimized for Condensed-Phase Applications-Overview with Details on Alkane and Benzene Compounds.J.Phys.Chem.B,vol.102,pp.7338-7364.

Sun,H.;Ren,P.;Fried,J.R.(1998):The COMPASS force field parameterization and validation for phosphazenes.Comput.Theor.Polym.Sci.,vol.8,pp.229-246.

1Department of Power Mechanical Engineering,National Tsing Hua University,Hsinchu 30013,Taiwan.

2Corresponding author.E-mail:cwhong@pme.nthu.edu.tw