基于双孔隙和三孔隙模型的缝洞型储层导电理论研究

高建申，王殿生，刘金玉，隋宏光

（中国石油大学（华东）地球科学与技术学院，山东 青岛266580）

0 引 言

关于孔隙介质岩石电学性质的研究可以追溯到20世纪30、40年代［1－5］。Archie［6］首次建立了地层电阻率因素与孔隙度的实验关系式，奠定了电阻率测井定量评价的理论基础，但是Archie公式不适用于孔隙结构复杂的缝洞型储层。因此，探索缝洞型储层岩石电学性质的新理论和新方法已经成为研究热点。

有学者在Archie公式基础上引入裂缝孔隙度，建立基质－裂缝双孔隙储层的导电模型［7－12］并分析裂缝对储层导电的影响［13－15］；引入了非连通孔洞孔隙度，建立含基质和非连通孔洞的储层导电模型［16－18］，着重分析非连通孔洞对储层导电的影响。还有学者建立裂缝－孔洞双孔隙介质的导电理论［19］；将基质孔隙、裂缝孔隙和孔洞孔隙综合在一起，建立三孔隙储层导电模型，并主要分析裂缝和非连通孔洞在储层导电过程中的不同作用［20－22］。还有学者从理论或实验分析储层电阻率与孔隙度的关系［23－24］，利用计算机模拟方法研究不同孔隙介质模型的电传输特性［25］，利用原生孔隙和次生孔隙研究碳酸盐岩储层中双孔隙结构对电阻率及胶结指数的影响［26］并对储层导电模型进行总结与评价［27－29］。

本文将具有复杂孔隙结构的缝洞型储层分为基质孔隙、裂缝孔隙和孔洞孔隙不同组合的概念模型，在Warren－Root电导模型的基础上，采用新的方法推导了基质、裂缝、孔洞不同组合的双孔隙和三孔隙储层电阻率模型的理论公式，并与其他理论和实验结果进行了对比分析。

1 双孔隙储层的电阻率理论模型

1．1 Warren－Root导电模型［7］

如图1所示，Warren和Root将非均质裂缝性储层等效为由小立方体组成的立方体阵；每一块小立方体代表岩石基质，内部含有基质孔隙或孔洞孔隙；小立方体之间的等间距空间代表裂缝，而且同方向的所有裂缝都是平行的。每一个裂缝与2个小立方体相邻，因此每一个小立方体单元由岩石基质部分（小立方体）和6个一半裂缝组成。Warren－Root等效模型在空间上具有周期性，所以一个小立方体单元的导电性质可以代表整个立方体阵的导电性质。

1．2 基质－裂缝型双孔隙储层的电阻率理论模型

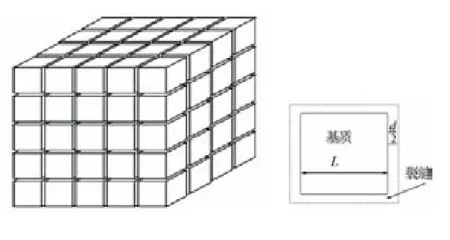
图1 Warren－Root等效模型及小立方体单元截面

在Warren－Root模型中取一个小立方体单元截面，岩石基质长度为L，裂缝宽度为d，裂缝边界用虚线表示（见图1）。如果不考虑基质岩石的导电性，基质孔隙可等效为n条横截面积相等的长度为L的毛细管，则基质孔隙度φb可表示为

式中，An表示n条毛细管的总横截面积；A表示岩石基质的横截面积。

裂缝孔隙度φf可表示为

含有基质孔隙和裂缝孔隙的双孔隙储层的电阻可以采用并联电阻网络结构等效。当100%饱和水时，双孔隙储层电阻R与基质电阻Rb和裂缝电阻Rf的关系为

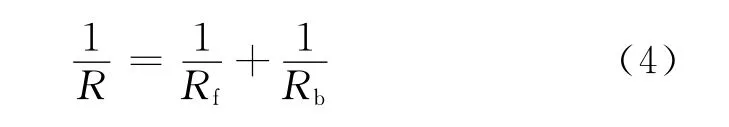
根据欧姆定律和地层因素定义，假设小立方体中与电流方向垂直的裂缝不参与导电，并考虑基质导电性，得出基质－裂缝型双孔隙储层地层因素为

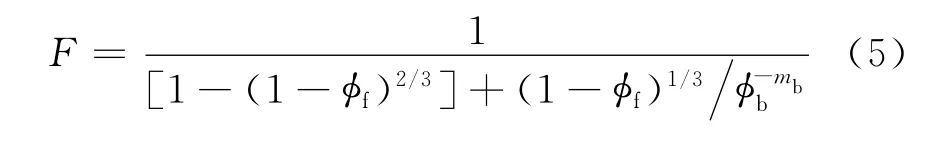
式中，mb为基质胶结指数，其值变化范围在1．6～2．4［8］。在实际应用中，仿照文献［10］将指数1／3、2／3分别改为0．39～0．45、0．78～0．90。

1．3 基质非连通孔洞型双孔隙储层电阻率理论模型

当储层中只含有基质孔隙和非连通同孔隙或裂缝孔隙不发育时，需要从宏观角度建立基质－非连通孔洞型双孔隙储层的电阻率模型（见图2），在小立方体单元中将空间上处于同一剖面上的非连通孔洞水平地放置在一端，整体上等效为长方体，采用基质－非连通孔洞串联模型计算整个系统的电阻。

设基质部分宽为h，则非连通孔洞部分宽为（L－h），非连通孔洞孔隙度为

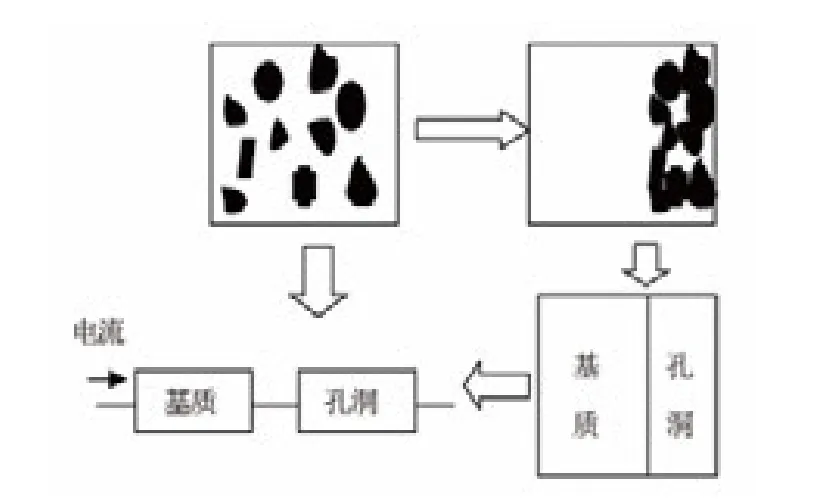
图2 基质－非连通孔洞等效模型

100%饱和水时基质－非连通孔洞型双孔隙储层的电阻为

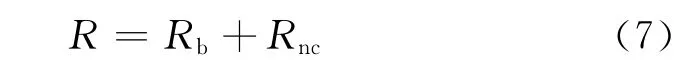
式中，Rnc为非连通孔洞的电阻，根据欧姆定律及地层因素定义得出基质－非连通孔洞型双孔隙储层的地层电阻率因素

式（8）与 Aguilera［11］得出的结果完全相同，但是后者没有提出怎样将该复杂的导电系统等效为串联电阻模型。

1．4 裂缝－非连通孔洞型双孔隙储层电阻率理论模型

对于裂缝－非连通孔洞型双孔隙储层的电阻，可采用裂缝与非连通孔洞的串联电阻模型计算。在不考虑基质孔隙度和基质岩石导电性且100%饱和水时，将裂缝和非连通孔洞串联得出裂缝－非连通孔洞型双孔隙储层的地层因素为

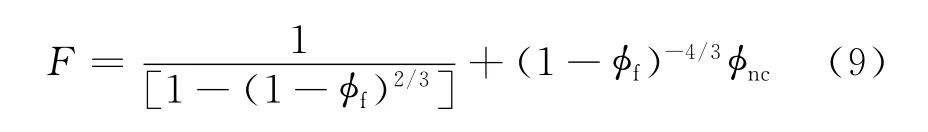
若考虑基质岩石的导电性，式（9）需要修正。

1．5 连通孔洞型双孔隙储层的电阻率理论模型

对于含有连通孔洞的双孔隙储层，连通孔洞的导电性可以等效为裂缝的导电性［11］，所以含有连通孔洞的储层可等效为含有裂缝的储层。因此式（5）和式（9）可改写为一般化形式，即

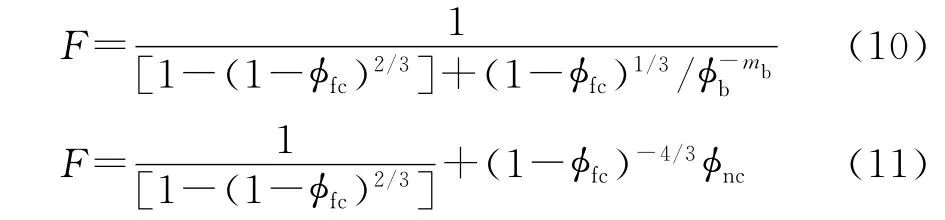
其中

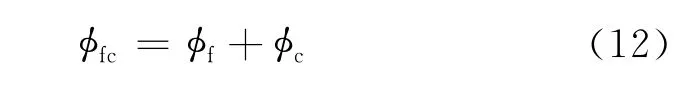
式中，φc为连通孔洞孔隙度；φfc为裂缝孔隙度和连通孔洞孔隙度之和。

2 三孔隙储层的电阻率理论模型

三孔隙储层是由基质孔隙、裂缝孔隙和孔洞孔隙组成的更为复杂的复合孔隙储层。在双孔隙储层电阻率理论模型基础上，采用基质与裂缝（连通孔洞）并联再与非连通孔洞串联的电阻模型建立三孔隙储层电阻率理论模型（见图3）。

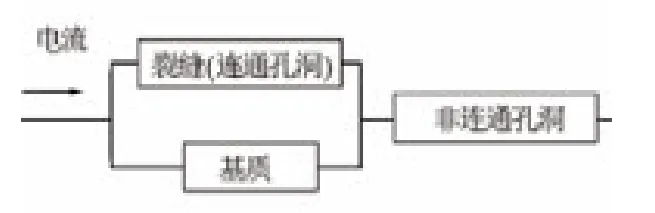
图3 三孔隙储层电阻率等效模型

三孔隙储层系统的电阻为

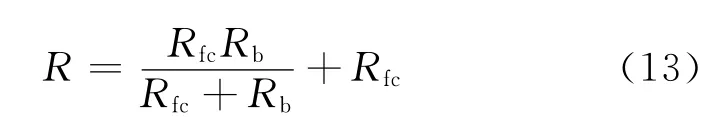
根据地层因素定义，参照前面各部分电阻的处理，得出基质－裂缝－孔洞复合孔隙储层的地层因素，即

式（14）与前面推导的双孔隙储层地层电阻率模型具有很好的兼容性，可简化为相应的双孔隙模型。

3 验证和分析

3．1 与相关理论结果的对比分析

Pérez－Rosales等［10］在 Warren－Root模型的基础上和忽略基质岩石导电性的前提下，建立了纯裂缝介质的导电理论模型，与前文推导的基质裂缝型双孔隙储层在只有裂缝时的情形一致，即

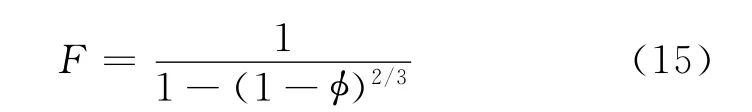
图4 纯裂缝储层F—φ曲线

图4给出了裂缝孔隙度范围为0．05～0．35时地层因素变化曲线。地层电阻率因素随着裂缝孔隙度的增加而降低，在孔隙度较低的范围内变化较显著；在孔隙度较高的范围内变化不明显。φ从0．05变化到0．15时，F从29．74变化到9．74，减小了20．00；φf从0．25变化到0．35时；F从5．73变化到4．00，仅减小了1．73。F与φ的关系用乘幂函数拟合为

图5给出了总孔隙度从0．05变化到0．20时F—φf曲线，并与 Aguilera［11］的结果比较，两者计算结果相差很小且曲线趋势规律一致。F与φf的关系也可以用乘幂函数拟合为

系数A和指数B随着总孔隙度的变化而改变（见图6）。系数A在总孔隙度为0．15时，达到最大值，指数B则随总孔隙度增大一直减小。

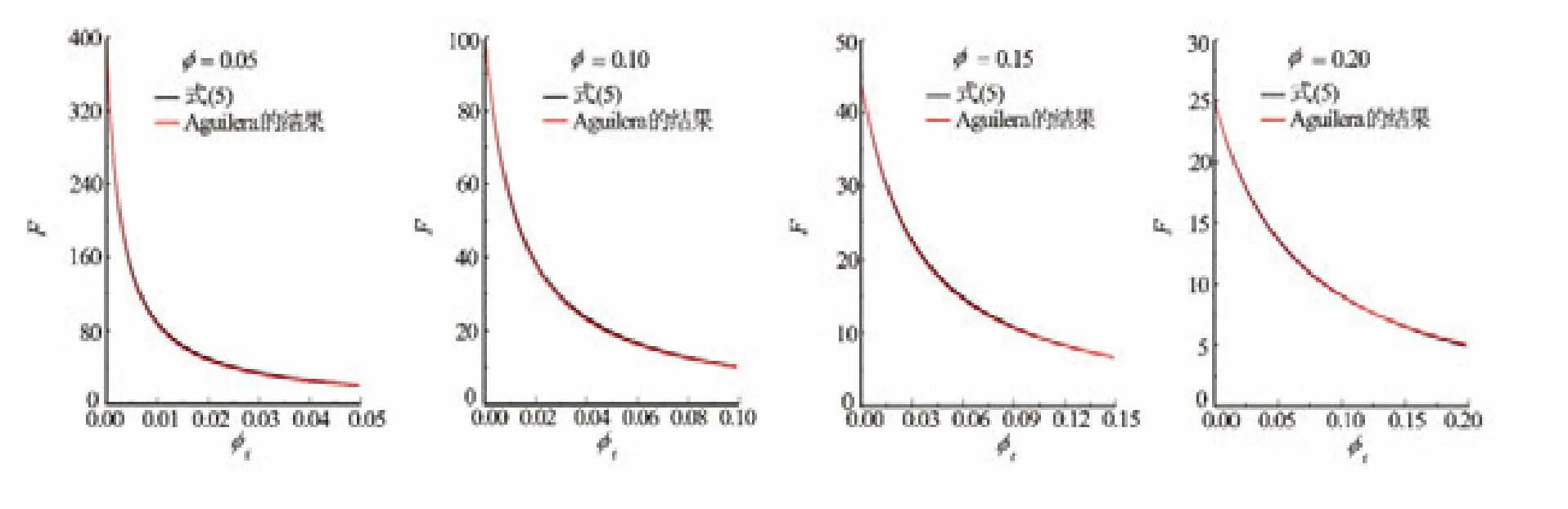
图5 与Aguilera双孔隙储层电阻率模型对比的F—φf曲线

图6 拟合乘幂函数系数A和指数B与总孔隙度的关系

从图5可见，在裂缝孔隙度很小时，F变化非常明显；当裂缝孔隙度大于总孔隙度的1／4以后，F值变化非常缓慢，说明了裂缝在储层导电过程中起主要作用，微小裂缝的出现使得岩石导电从以基质路径为主变化为以裂缝路径为主，发生质的变化。总孔隙度很低时对应的地层电阻率因素值很高，随着总孔隙度的增加，地层电阻率因素降低。

图7给出了总孔隙度从0．05变化到0．20，基质孔隙度占总孔隙度的一半，三孔隙储层电阻率模型的F—φf曲线，并与 Aguilera［20］结果对比，两者计算结果吻合得很好；裂缝在三孔隙储层导电过程中同样起主要作用。由于非连通孔洞的存在，三孔隙储层的F值大于基质－裂缝型双孔隙储层的F值。

图8给出总孔隙度从0．05变化到0．20，裂缝孔隙度占总孔隙度的比例为10%的三孔隙储层电阻率模型F—φnc曲线。从图8中可以看出，F随着φnc的增加而变大，但是变化不超过10%，说明裂缝存在时，非连通孔洞对储层导电性影响较小。

图7 与Aguilera三孔隙储层电阻率模型对比的F—φf曲线

图8 与Aguilera三孔隙储层电阻率模型对比的F—φnc曲线

3．2 与实验结果对比分析

图9给出了式（5）与 Pérez－Rosales等［10］实验结果的对比曲线，理论计算与实验结果变化趋势相同，数据点吻合。

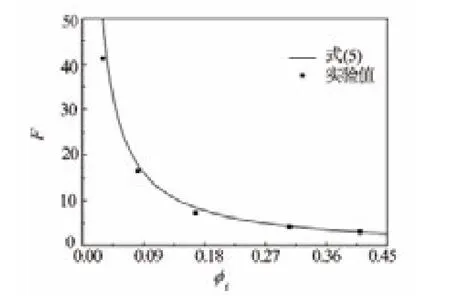
图9 纯裂缝储层电阻率理论与实验结果的比较

根据式（8）作出非连通孔洞孔隙度占总孔隙度的比值与胶结指数的关系曲线（见图10）。图10显示的胶结指数与非连通孔洞孔隙度占总孔隙度比值的关系与Luica［16］给出的实验测量结果（见图11）趋势符合得很好。当总孔隙度一定时，非连通孔洞孔隙度占总孔隙度比值越大对应的胶结指数越大，说明储层电阻率值越高。非连通孔隙度为0时，图10中所有曲线对应的胶结指数都为2．0，即为基质胶结指数。当非连通孔洞孔隙度占总孔隙度的比值一定时，总孔隙度越大对应的胶结指数越大，这是由非连通孔洞在储层导电过程中的阻碍作用导致的。在选定的总孔隙度为0．05～0．20范围内，胶结指数变化范围为2．0～4．5。

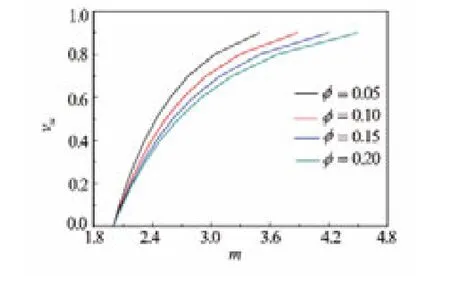
图10 非连通孔洞孔隙度占总孔隙度比值与胶结指数关系

图11 非连通孔洞占总孔隙度的比例与m关系［16］

表1给出了根据所建立的各类储层导电模型计算出的胶结指数和涂立新等［22］测量出的塔河油田碳酸盐岩不同孔隙类型储层的胶结指数。由表1可知，除了总孔隙度非常小的基质－裂缝（连通孔洞）储层的胶结指数计算值与实测值有一定的偏差之外，其余的都很一致。这是因为，在总孔隙度非常小（小于1%）时，裂缝张开度很小，有的地方甚至被全部压实，流体在裂缝中流动受阻，流通路径更加曲折，此时仍然用 Warren－Root模型等效储层会存在较大偏差。

表1 储层电阻率模型计算的胶结指数与实测值比较

4 结 论

（1）基于Warren－Root模型采用电阻网络串并联方法建立了双孔隙／三孔隙储层的电阻率理论模型。通过与相关理论模型和实验结果对比验证表明，所建立的理论模型能够很好地计算100%饱和水的缝洞型储层的电阻率，但是其应用于孔隙度值非常低（低于1%）的储层时存在较大偏差。

（2）储层电阻率理论模型可计算胶结指数。对于基质－非连通孔洞储层，当总孔隙度为0．05～0．20时，胶结指数随着非连通孔洞占总孔隙度比例的增大而增加，变化范围为2．0～4．5。

（3）裂缝对缝洞型储层的电阻率起主要作用，地层中微小裂缝的存在可以大大提升地层的导电能力。地层电阻率因素与裂缝孔隙度之间可以用乘幂函数拟合，拟合公式的系数和指数与总孔隙度有关。

（4）非连通孔隙的存在可增大缝洞型储层的电阻率，但增大作用较小；裂缝孔隙度大于10%的条件下地层电阻率因素的增加量小于10%。

（5）双孔隙／三孔隙储层电阻率理论模型可更细致地分析不同类型孔隙在缝洞型储层导电中所起到的作用，对于定性或定量认识复杂孔隙结构储层导电过程具有指导性作用。

［1］Wyckoff R D，Botset H G．The Flow of Gas－liquid Mixtures Through Unconsolidated Sands［J］．Physics，1936，7（9）：325－345．

［2］Jakosky J J，Hopper R H．The Effect of Moisture on the Direct Current Resistivities of Oil Sands and Rocks［J］．Geophysics，1937，2：33－55．

［3］Martin M，Murray G H，Gilngham W J．Determination of the Potential Productivity of Oil－bearing Formations by Resistivity Measurements［J］．Geophysics，1938，3：258－272．

［4］Leverett M C．Flow of Oil－water Mixture Through Unconsolidated Sands［C］∥ Trans AIME，1939，132：149－171．

［5］Guyod H．Fundamental Data for the Interpretation of Electric Logs［J］．The Oil Weekly，1944，115（38）：21－27．

［6］Archie G E．The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics［C］∥Trans AIME，1942，146：54－62．

［7］Warren J E，Root P J．The Behavior of Naturally Fractured Reservoirs［J］．SPE Journal，1963，3（3）：245－255．

［8］Aguilera R．Analysis of Naturally Fractured Reservoirs from Conventional Well Logs［J］．Journal of Petroleum Technology，1976，28（7）：764－772．

［9］Prison S J．Log Interpretation in Rocks with Multiple Porosity Types－water or Oil Wet［J］．World Oil，1957，6：196－198．

［10］Perz R，Mercado D，CruzHernan D，et al．New Formulation for Formation Resistivity Factors of Fractured Porous Media［C］∥SPE International Petroleum Conference and Exhibition，SPE Paper 58991，February 2000．

［11］Aguilera M S，Aguilera R．Improved Models for Petrophysical Analysis of Dual Porosity Reservoirs［J］．Petrophysics，2003，44（1）：21－35．

［12］Aguilera R．Effect of the Fracture Porosity Exponent（mf）on the Petrophysical Analysis of Naturally Fractured Reservoirs［Z］．Servipetrol Ltd，2006．

［13］Rasmus J C．A Variable Cementation Exponentmof Carbonate Pore Systems［J］．The Log Analyst，1983，24（6）：13－23．

［14］Stesky R M．Electrical Conductivity of Brine－saturated Fractured Rock［J］．Geophysics，1986，51（8）：1585－1593．

［15］Rasmus J C．A Summary of the Effects of Various Pore Geometries and Their Wettabilities on Measured and In－situ Values of Cementation and Saturation Exponents［J］．The Log Analyst，1987，28（2）：152－164．

［16］Luica F J．Petrophysical Parameters Estimated from Visual Descriptions of Carbonate Rocks：A Field Classification of Carbonate Pore Space［J］．Journal of Petroleum Technology，1983，35（3）：629－637．

［17］Towle G．An Analysis of the Formation Resistivity Factor－porosity Relationship of Some Assumed Pore Geometries［C］∥ SPWLA Logging Symposium，Trans，1962．

［18］Focke J W，Munn D．Cementation Exponents in Middle Eastern Carbonate Reservoirs［J］．SPE Formation Evaluation，1987，2（2）：155－167．

［19］Perz R，Mercado D，CruzHernan D，et al．Electric Resistivity of Vuggy Fractured Media［C］∥SPE International Petroleum Conference and Exhibition，SPE Paper 74340，February 2002．

［20］Aguilera R F，Aguilera R．A Triple Porosity Model for Petrophysical Analysis of Naturally Reservoirs［J］．Petrophysics，2004，45（2）：157－166．

［21］王青，李国平，赵新民．复杂储集空间储集层测井解释方法研究［J］．测井技术，2003，27（5）：389－393

［22］涂立新，樊政军，李宗杰，等．塔河油田碳酸盐岩储层三孔隙度测井模型的建立及其应用［J］．石油物探，2010，49（5）：489－494．

［23］李宁．电阻率—孔隙度、电阻率—含油（气）饱和度关系的一般形式及其最佳逼近函数类型的确定（I）［J］．地球物理学报，1989，32（5）：580－591．

［24］毛志强，谭廷栋，林纯增，等．完全含水多孔岩石电学性质及其孔隙结构实验研究［J］．石油学报，1997，18（3）：51－55．

［25］岳正文，陶果，朱克勤．饱和多相流体岩石电性的格子气模拟［J］．地球物理学报，2004，47（5）：905－910．

［26］徐朝晖，焦翠华，王绪松，等．碳酸盐岩地层中双孔隙结构对电阻率及胶结指数的影响［J］．测井技术，2005，29（2）：115－117．

［27］潘宝芝，张丽华，单刚义，等．裂缝和孔洞型储层孔隙模型的理论进展［J］．地球物理学报，2006，21（4）：1232－1237．

［28］王敏，张丽艳，孙建孟，等．碳酸盐岩储层孔隙模型及孔隙结构指数研究进展［J］．西安石油大学学报：自然科学版，2010，25（3）：1－7．

［29］张丽华，潘保芝，单刚义．孔隙度指数m确定方法研究进展［J］．地球物理学进展，2010，25（3）：975－981．