An Evaluation of Multigrid Acceleration for the Simulation of an Edge FLame in a Mixing Layer

M.Wasserman,Y.Mor-Yossefand J.B.Greenberg

1 Introduction

In a recent PhD thesis Wasserman(2014)presented a comprehensive multi-grid based numerical strategy for RANS(Reynolds-averaged Navier-Stokes simulations)of steady state turbulent reacting flows.The study was motivated by the constantly growing complexity of turbulent combustion CFD simulations,imposing severe demands on computational resources.Such demands often render the simulation of practical,supersonic reacting flows over complex geometries unaf-fordable.As standard numerical methods are inefficient in solving the highly stiff,reacting(RANS)equations which govern turbulent combustion,there exists a need for methods that accelerate the iterative convergence to a steady-state.

Perhaps the foremost problem associated with numerical solution of the equations governing reacting flow is the strong numerical stiffness.A given set of differential equations is considered numerically stiff when the physical processes described by it(e.g.,convection,diffusion and chemical reaction)develop on very different time scales,or equivalently,when the corresponding eigenvalues of the discretized,algebraic equation set vary greatly[Gear(1971)].Numerical stiffness may significantly limit convergence rates of standard iterative methods,and results in lack of robustness of numerical simulations,unless properly treated[Lomax,Pulliam and Zingg(2001].The numerical stiffness of the reacting RANS equation set may be attributed to several factors.In high Reynolds number applications prominent in aeronautical engineering,extremely dense meshing is employed near solid walls to accurately resolve boundary layers,leading to highly stretched cells.As a result,the characteristic time scales of convection and diffusion processes may differ considerably,and the resulting eigenvalues of the system may be spread over a wide range of values.This effect may be noted even in some non-reacting,laminar simulations.Moreover,finite-rate chemistry and turbulence modeling introduce severe numerical stiffness owing to the nature of source terms appearing in both models.The source terms which represent the production and dissipation of turbulence,and the transformation of species due to chemical reactions,are often strongly nonlinear and contain time scales that greatly differ from those of the convective and diffusive terms.The turbulence dissipation time scale may vary by many orders of magnitude across a turbulent boundary layer,and can be vastly different from the other time scales(e.g.molecular diffusion and wave propagation).In addition,chemical kinetics,especially for combustion,is characterized by widely disparate time scales related to formation and depletion of different species.In high-speed combustion of hydrogen with air,for instance,the characteristic time scales of hydroxyl(OH)formation are extremely short(10−8sec.),while the characteristic time scales of water vapor formation are relatively long(10−2sec.)[Bussing(1985)].It is this time-scale disparity that leads to numerical stiffness.Any numerical approach aimed at solving the RANS equations coupled with turbulence and/or chemistry model equations should be able to reflect all the different time scales present in the flow to ensure stability and accuracy.To comply with this requirement,the allowed time-step is limited by the rate of the fastest chemical reaction.

Geometric multigrid(MG)methods are amongst the fastest numerical acceleration techniques known today.Basically,MG methods accelerate convergence rates of numerical schemes by using a hierarchy of grids,based on the notion that some nu-merical error modes are more efficiently treated on a coarse grid than on a fine grid.However,a coarse grid may only be used in conjunction with a finer one,requiring proper data transfer between consecutive grids.MG methods rely on two basic principles:Smoothing and Coarse Grid Correction(CGC).First,standard iterative methods(e.g.,Gauss-Seidel)with good smoothing(that is,elimination of high spatial frequency modes)properties are used to treat non-smooth errors in the solution.Pre-smoothing is required because only a smooth error is represented well on both fine and coarse grids,while non-smooth errors exhibit aliasing on coarse grids,significantly reducing the efficiency of coarse grid corrections[Yavneh(2006)].After a smooth error is obtained on the finest grid where a solution is sought,relaxation continues on coarser grids which are achieved by eliminating every other grid line in each coordinate direction(on structured grids).A coarse grid relaxation is substantially cheaper(up to four times in 2D)than its fine grid counterpart,and is also more efficient in eliminating errors which are relatively smooth on a finer grid.Thus,efficiency can be increased by transferring(restricting)some of the fine grid iterations required for convergence,to a coarser grid,and interpolating(prolongating)the results,that is,applying a coarse grid correction,to advance the solution on the finest grid.MG methods are widely popular,and well defined in a mathematical sense[Briggs and McCormick(2000),Trottenberg,Oosterlee,and Schuller(2001)].Beginning with the pioneering work of Brandt(1977),who first presented an unprecedented efficiency of MG methods for elliptic boundary-value problems,and the Full Approximation Storage(FAS)MG method for nonlinear equations,many researchers have been using this class of methods in a wide variety of fields such as CFD,image processing and medical science.

However,while for simple model problems based on elliptic PDEs,optimal textbook multigrid efficiency(TME)[Trottenberg,Oosterlee,and Schuller(2001)]was demonstrated more than three decades ago[Brandt(1977)],modern MG methods for mixed-nature,non-linear equations such as the RANS equations are still far from optimal[Brandt(1998)].For instance,MG methods for the Navier-Stokes equations are known to suffer from convergence difficulties in high Reynolds viscous flows.The successful incorporation of turbulence and species mass transport equations in the multigrid framework still remains a major barrier to demonstrating an optimally efficient MG method for the reactive RANS equations[[Brandt(1998)]].Indeed,finite-rate chemistry currently poses a significant challenge for standard multigrid methods.In the case of a full coarsening multigrid strategy,coarse grid variables are linearly calculated from corresponding fine grid values.Recalculation of strongly non-linear chemical kinetics source terms on coarse grids based on linearly averaged variables may cause large differences compared to finegrid values.In most cases,the consequence is divergence of classic multigrid schemes[Gerlinger,Mobus and Bruggemann(2001)].Moreover,since chemical reaction zones are usually very small,coarse grid level solutions may not sufficiently resemble those obtained on the fine grid levels[Edwards and Royt(1998)].For example,if fuel and oxidizer are separated on a grid with fine resolution,this is not necessarily the case in an equivalent coarse grid level where mixing(combustion)may occur due to insufficient spatial resolution.To overcome these difficulties,extensive stabilization is employed by the few researchers who published results of attempts at applying multigrid to chemically reacting flows.

Sheffer,Jameson and Martinelli(1998)only managed to achieve convergence using a two-level,explicit multigrid simulation of detonation waves.Slomski,Anderson and Gorski(1990)simulated reacting flows using standard multigrid procedures,but demonstrated acceleration only for low supersonic flows with reduced chemical kinetics models.Edwards(1996)applied multigrid to hypersonic chemically reacting flows and hydrogen combustion[Edwards and Royt(1998)],but had to employ global damping of the restricted residuals and lowered CFL numbers on coarse grids to stabilize the solution.To avoid global damping,a local damping of the restricted residual in regions of high chemical activity was suggested by Gerlinger,Mobus and Bruggemann[(2001)]and Gerlinger(2005),allowing for harvesting the full potential of multigrid in regions without combustion.Kim,Kim and Rho(2001)employed a damped prolongation procedure based on the ratio of local pressure values from the coarse and fine grids to damp coarse-grid corrections in the vicinity of shock-waves.Bellucci and Bruno(2001)were able to devise a four-level multigrid method for three-dimensional incompressible flows with combustion.However,they applied Laplacian smoothing of coarse-grid corrections and presented convergence rates only for non-reacting cases.Another drawback of all approaches mentioned is the dependence on user-supplied parameters which significantly lowers the robustness of multigrid reacting flow simulations[Gerlinger(2005)].

To overcome the aforementioned difficulties Wasserman(2014)proposed using the unconditionally positive-convergent(UPC)time integration implicit scheme[Mor-Yossef and Levy(2006,2007,2009)and Wasserman,Mor-Yossef,Yavneh and Greenberg(2010)]originally developed for turbulence model equations,and successfully extended its use with chemical kinetics models,in a fully-coupled multigrid(FC-MG)framework.

To tackle the degraded performance of multigrid methods for chemically reacting flows,two major modifications were introduced with respect to the basic Full Approximation Storage(FAS)multigrid method.First,a novel prolongation operator based on logarithmic variables was proposed to avoid loss of positivity due to coarse grid corrections.The use of a positivity-preserving prolongation operator,together with the extended UPC implicit scheme,ensure unconditional positivity of turbulence quantities and species mass fractions throughout the multigrid simulation.Secondly,in order to improve the coarse grid correction obtained in localized regions of high chemical activity,a modified defect correction procedure was devised,and successfully applied for the first time to solve turbulent,combusting flows.The proposed modifications to the standard multigrid algorithm created a well-rounded robust numerical method that provides accelerated convergence with respect to an equivalent single-grid-based method,and unconditionally preserves the positivity of model equation variables.The resulting MG method is suitable for robust simulations of a wide range of flows thanks to being nearly completely free of artificial stabilization techniques.

Numerical simulation of various turbulent and reacting flows showed that the proposed MG method increases the efficiency by a factor of up to eight(8!)times with respect to an equivalent single-grid method,and by two times with respect to an artificially-stabilized MG method.Moreover,the method has proven to be more stable than an equivalent SG-based method,allowing the use of higher CFL numbers,and rapid convergence in cases where the SG-based method failed to converge.

The majority of examples of reacting flow to which MG was applied involved premixed reacting flows and employed various degrees of chemical complexity in terms of the actual details of the participating elementary chemical reactions.It is well-known that the nature of non-premixed combustion is rather different[Williams(1985)and Law(2006)]and little attention has been paid to acceleration of numerical schemes for dealing with non-premixed reacting flows.

In the present paper we present a first evaluation study of the application of multigrid acceleration for the simulation of an edge flame in a laminar mixing layer.The main purpose of the investigation is to provide initial insight into the relevance and/or scope of multigrid acceleration in this context without the additional complexities of turbulence.

2 Mathematical Model and Assumptions

We consider two parallel streams of equal(constant)laminar velocity,one of gaseous fuel and the other of oxygen.The two streams are separated upstream by a semiinfinite flat plate(see Figure 1).The temperature of the plate is assumed constant and equal to the upstream temperature of the two streams.Downstream of the plate,under appropriate operating conditions,chemical reaction occurs.It will be taken to be represented by a single global reaction step of the form:

Fuel+ ν Oxidizer→ (1+ν)Products+thermal energy,where ν is the stoichiomet-ric coefficient.

Figure 1:Configuration for study of an edge flame:the broken line.

Downstream of the tip of the plate diffusive mixing of the fuel and oxygen occurs and a mixing layer is formed.What is known as an edge flame arises,located somewhere downstream of the plate’s tip.We refer to this edge flame as the root of the diffusion flame that is attached to and trails downstream from it.When there is only moderate premixing of reactants the edge flame is characterized by a reaction kernel with a volumetric reaction rate much greater than that of the trailing diffusion flame.In Fig.1 typical reaction rate contours are shown.Because of the premixing zone before the onset of reaction the entire structure of the flame is that of a partially premixed flame(at the root)followed by a trailing downstream diffusion flame.This configuration was examined numerically by Kurdyumov and Matalon(2004)with particular emphasis on the dynamics of such flames.In the current work we concentrate on obtaining steady state solutions using multigrid acceleration.

Further reasonable assumptions which are adopted are that the density of the gas mixture,ρ,the thermal diffusivity,Dth,the specific heat capacity at constant pressure,Cp,and the molecular diffusion coefficients of fuel and oxidant,DF,DO,respectively,are constant.Under these and the aforementioned assumptions we obtain the following non-dimensional thermal-diffusional formulation of the governing equations:

In these equationsYFandYOare the mass fractions of the fuel and oxidant,respectively,normalized relative to their far-upstream values,YF0,YO0,θ=(T−T0)/(Ta−T0)is the normalized temperature withTathe adiabatic temperature andT0the temperature of the fuel and oxidant streams upstream as well as the fixed temperature of the splitter plate and φ = νYF0/YO0the mixture strength.his the volumetric heat loss term given byh=(1+γθ)4−1 andbis its coefficient,with the heat release parameter γ=(Ta−T0)/T0.LeF,LeOare the Lewis numbers of the fuel and oxygen,respectively,taken here as unity for the sake of simplicity.Finally,the non-dimensional chemical reaction rate term is

where

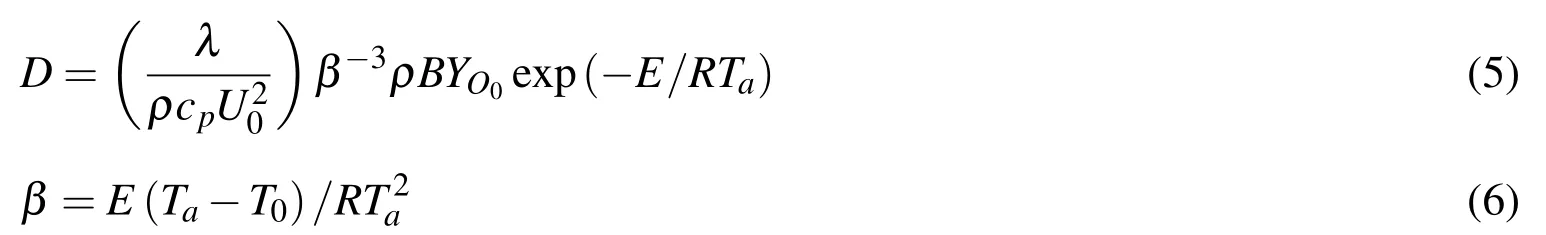
In Eqs.(5)and(6)Dis the Damkohler number,U0is the constant velocity of the mixture,λ its thermal conductivity,Bthe pre-exponential coefficient,Ethe activation energy andRthe universal gas constant.The Damkohler number is a ratio of typical flow to chemical reaction times and essentially plays the dominant role in determining the downstream location of the flame relative to the splitter plate.

For the ensuing numerical formulation we write the governing equations in vector form:

in which

and

Finally,to close the problem mathematically we specify the boundary conditions:

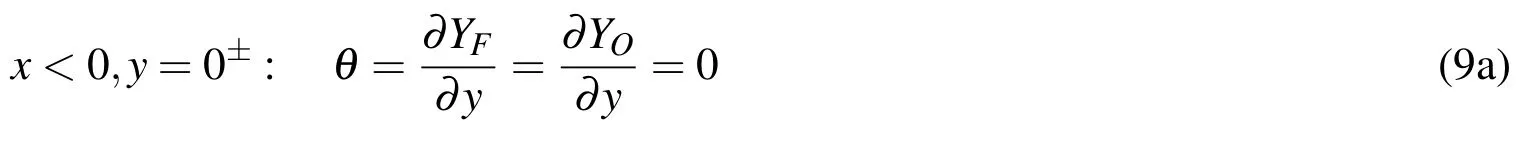
The first boundary conditions represent conditions on the splitter plate which is at fixed normalized temperature(i.e.zero)and is impervious to mass transfer.The second conditions relate to conditions far upstream above the splitter plate as well as at the upper boundary of the domain.Similarly,the third conditions give conditions far upstream below the plate as well as at the lower boundary of the domain.Finally,the last conditions state that far downstream no changes occur in the mass fractions and the temperature.

The finite solution domain and the aforementioned boundary conditions are shown schematically in Fig.2.

Figure 2:Schematic of solution domain and boundary conditions.

3 The Numerical Approach

Finite differences are utilized for discretization of the governing equations and the relevant boundary conditions.Using subscriptsi,j,for thexandydirections,respectively and Δx,Δyfor increments in those directions we have:

where we takex1=−5,xN=15,y1=−15,yM=15 so that conditions at the far boundaries are well represented.NandMwere chosen to ensure that the tip of the splitter plate,(x,y)=(0,0),is a mesh point.In this work thexandyincrements were both taken equal toh.

The governing equations were discretized using central differences for the spatial derivatives so that for non-boundary points

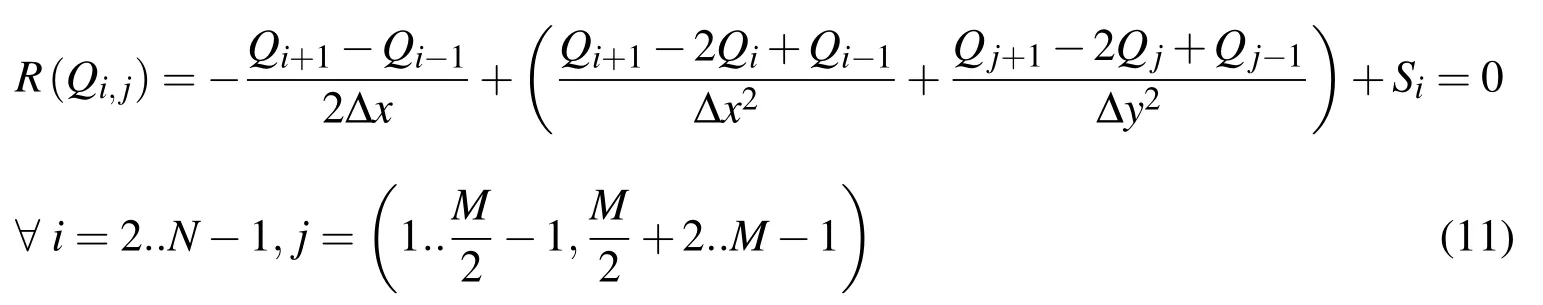
The boundary conditions become:

At the upper and lower boundaries:

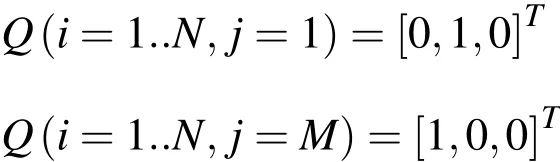
On the lower and upper sides of the splitter plate second order backward and forward differences are used,respectively,for the mass fraction derivatives:

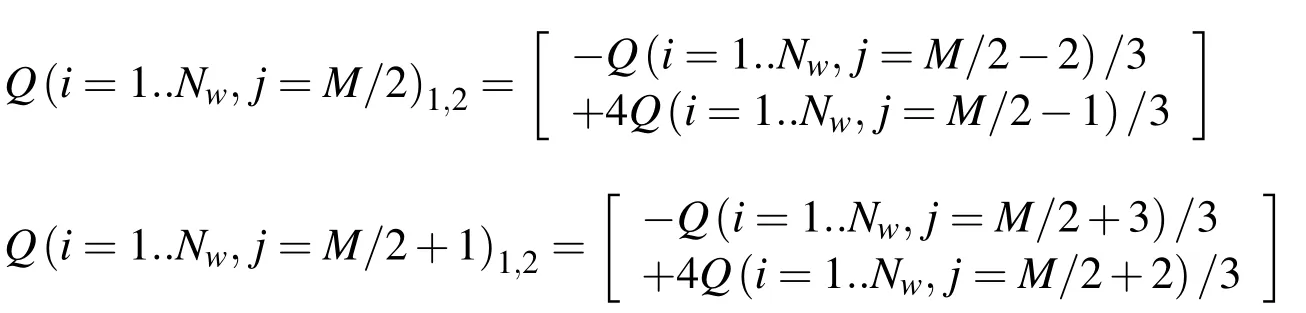
where the subscripts"1,2"relate to the fuel and oxidant mass fractions,respectively,and"w"to the value on the wall(plate).

For the temperature along the plate:

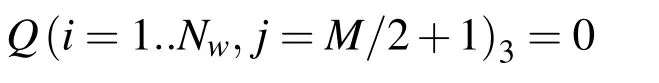
In the far field:

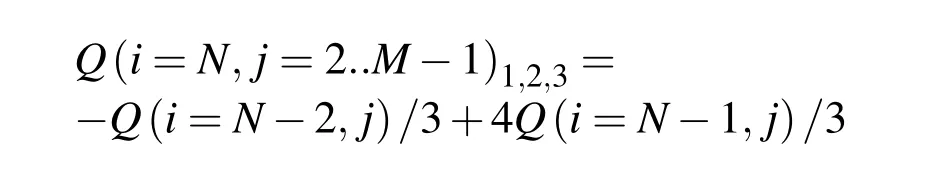
The subscript"3"refers to the normalized temperature which is the third component of the vectorQ.

At the left hand(entrance)boundary below the splitter plate

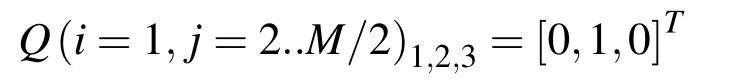
whereas above it

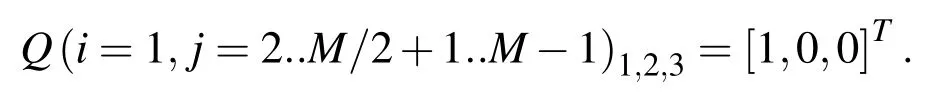
4 The Numerical Solution

4.1 Basic solution method

The point Jacobi method is employed for solving the set of nonlinear algebraic equations that replace the original governing equations.The advantages of this method lie in its ability to be readily parallelized for large problems and its efficient error smoothing property which is essential for effective application of the multigrid method.The point Jacobi scheme relevant to the current problem at any point in the solution domain and for iteration numbernis

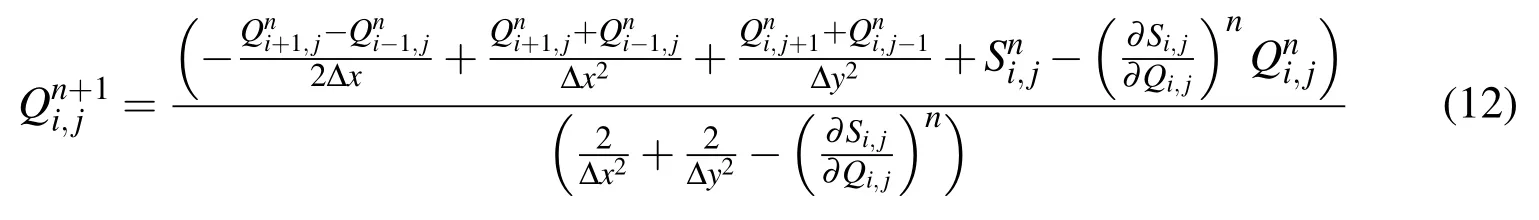
Note that the source term has been linearized about the previous iteration.

The analytical Jacobian is given by

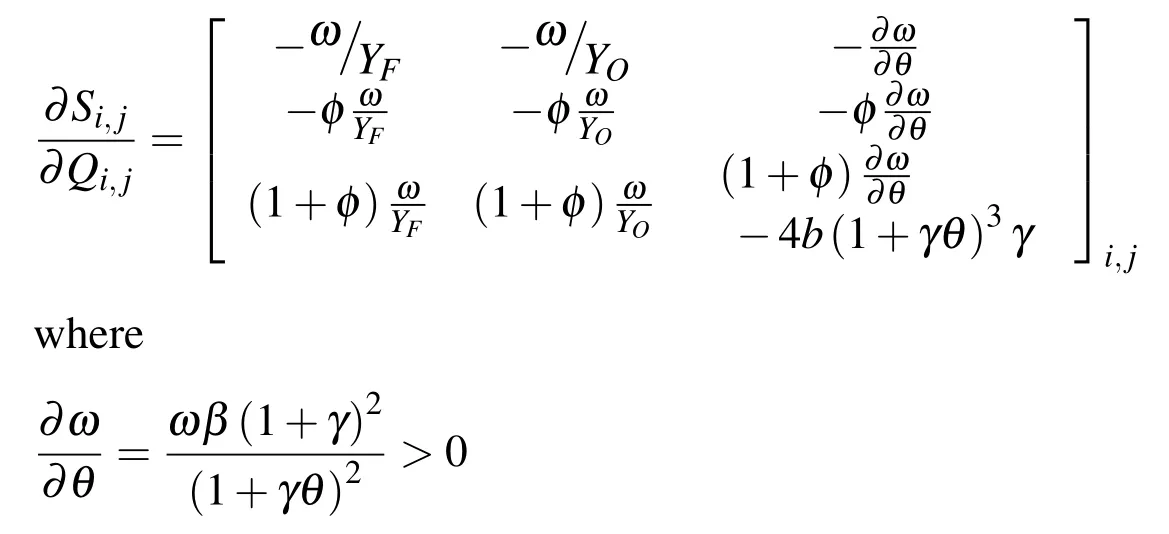
To allow for larger time-steps,an implicit solution is sought,requiring that all eigenvalues,λiof the Jacobian,∂Si,j/∂Qi,j,satisfyRe(λi)＜ 0.

For this purpose,use is made of an approximate source term Jacobian of the form

For convenience the actual Jacobian was diagonalized since when convergence to a steady state is attained this term becomes irrelevant.Diagonalization contributes to computational efficiency as it preserves a scalar partitioning at each iteration In addition,the positive term(stemming from the temperature Jacobian terms)was omitted because of stability considerations.

For the purpose of stability and error smoothing under-relaxation was also utilized:

with a value of 0.9 assigned to the relaxation parameterw,providing optimal performance for most of the cases studied here.

The initial guess was based on an analytical solution of the problem which can be deduced when the Damkohler number tends to infinity.For further details the interested reader is referred to Kurdyumov and Matalon(2004)

The convergence of the iterative procedure was checked using the following criterion

4.2 Multigrid application

Because of the strongly nonlinear nature of the problem FAS multigrid was applied.With this method the discrete problem is solved on a hierarchy of meshes of different levels of refinement obtained by deleting every second point in each direction of the basic mesh(h)as sketched in Fig.3.

In order to obtain significant iterative convergence it was necessary to employ at least three levels of mesh refinement.

The stages of application of the multigrid method are enumerated here:

(1)Fine-grid pre-relaxation:Rh（Qh）=dh.

A number of point-Jacobi iterations with under-relaxation are performed in order to smooth the error(dh).

(2)Restriction to a coarser grid:in whichis the coarsening operator andQ¯his the approximation toQh.In order to obtain a significant contribution to the solution from the finer grid the error from the finer grid is transferred to the coarser grid using a coarse grid operator

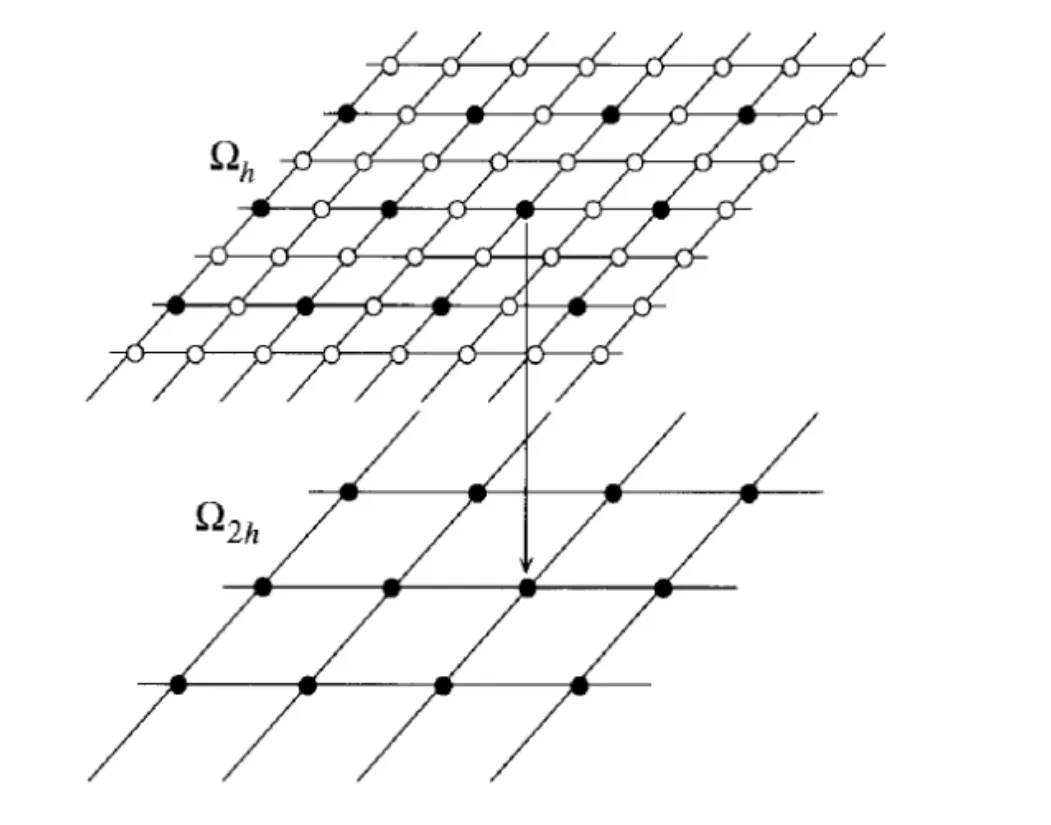
Figure 3:A coarse mesh obtained by deleting every second point of the basic mesh.

comprised of weighted neighboring values from the fine grid as per the following:

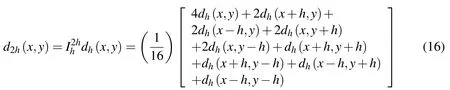
The error that is transferred acts as a source term that“drives”the solution on the coarser grid thereby contributing to decreasing the error on the finer grid.

In some cases,specifically at the early stages of the numerical simulation,the finegrid residual is very large,and not necessarily smooth,so that when it is transferred to the coarse-grid,it may result in divergence due to aliasing and due to the highly non-linear nature of chemical source terms.To avoid this,a damped restriction operator is introduced,as follows:

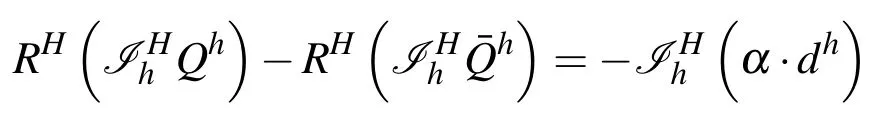
where α is a positive damping factor,taken to be smaller than one.In this work two possible methods of damping the error transferred to the coarse grid,dh,were considered:

(a)local damping of the transferred error only in regions where significant chemical reaction occurred,via the following formula[Gerlinger,Mobus and Bruggemann(2001)]:

and(b)fixed global reduction of the transferred error.

The different strategies for determining α are compared in section 5.

A number of iterations of the point Jacobi method with under-relaxation are carried out to obtain a better approximation,,which satisfies the equation that includes the error term from the fine grid on the coarse grid.After carrying out these iterations one can return to the finer grid or apply the algorithm recursively(i.e.to transfer to an even coarser grid in order to obtain an even better solution to the equation on the coarser grid).

The correction from the coarser grid is transferred to the finer grid where it is used to update the current approximation to the solution.The interpolation operator,,used to transfer the correction to the finer grid(prolongation)is bi-linear interpolation,as illustrated in Fig.4.

The afore-described multigrid stages were applied cyclically,in a V-cycle,as sketched in Fig.5.Since cycling replaces single grid iteration additional computation is required.In order to be able to correctly compare between achievement of convergence using multigrid and via a single grid we will use work units(WU).Each work unit is equivalent to the computer time necessary to carry out a single iteration on the finest grid in the hierarchy.

Key to interpolation

Figure 4:The bi-linear interpolation operator.

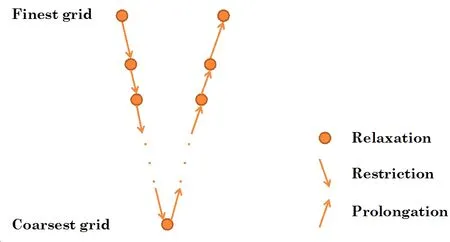
Figure 5:The structure of the V-cycle for the multigrid method.

5 Numerical Results

5.1 Introductory comments

In this section numerical results obtained using the afore-described numerical method are discussed.Ideally,a test problem for which an analytical solution exists would be appropriate to choose for comparative and validation purposes.However,it is well known that for diffusion flames no such solution exists unless an infinite chemical Damkohler number limit is taken,in which case the flame front region simply collapses to a surface(a curve in 2D)across which matching conditions are applied.This negates the purpose for which the current multigrid study is conducted,viz.to evaluate the method’s robustness under circumstances in which a thin,yet finite,reaction zone exists.Thus,the problem under consideration does not admit an analytical solution so that comparison with the computed results from Kurdyumov and Matalon(2004)was used as an index of the veracity of the results produced by the current approach.Furthermore,a grid convergence study was conducted to determine the optimal mesh size.Table 1 shows the key,most sensitive characteristics of the problem,the predicted location(xw,yw)and value(ωmax)of the maximum chemical reaction rate obtained for the standard set of parameters employed in this work(φ=5,D=12,b=2e-4).

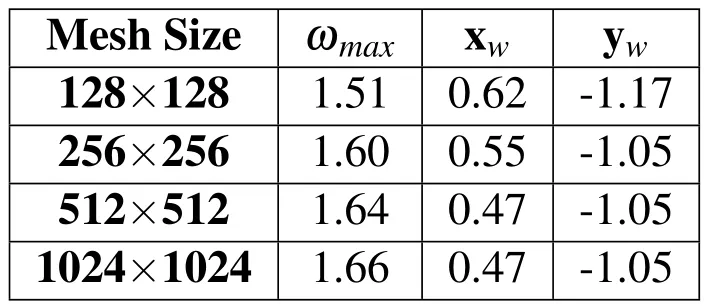
Table 1:Grid convergence study(φ=5,D=12,b=2e-4).

The predictions obtained with the 512×512 and 1024×1024 mesh sizes are virtually identical,demonstrating grid convergence.Therefore,a 512×512 mesh was employed throughout this work.

Figure 6 illustrates the ability of the current approach to reproduce the solution for the edge flame(the colored part shows the reaction rate and the continuous lines temperature contours).This figure should be compared to Figure 2 of Kurydumov and Matalon(2004)in which the reaction rate contours are shown as solid lines and the temperature contours as broken lines.Although the scaling is different and the values of the contours in that reference are not stated the general agreement is very good.Indeed,good agreement was obtained for other comparisons like this,thereby providing good validation for the current approach.

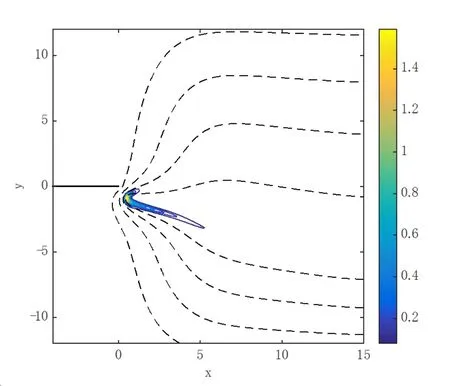
Figure 6:Flame structure results for comparison with results of Kurydumov and Matalon(2004);data as in tex.

5.2 Multigrid performance

As mentioned in section 4.2,the sharp nonlinearity and the very local nature of the chemically related source terms tend to render achieving a converged solution using multigrid almost impossible.The difficulty stems from the inability to correctly represent the chemical source term on coarse grid levels.In addition,all multigrid methods are predicated on smoothness of the error transferred to the coarse grid.With chemical activity present the source term does not permit such smoothness.To overcome the problem two methods were implemented(local(Eq.(17)and global damping).In Figure 7 a comparison between the applications of these two forms of damping is shown.It can be seen that local damping enables slightly faster convergence than global damping but at a price of the extra work involved in computing how much damping should be applied at each point(i.e.,computing α(ω)at each grid point).

In view of this comparison global damping seems to be preferable and thus α=0.8 was chosen for all further results that will be presented for whichD＜1000.In order to enable convergence for larger Damkohler numbers(D≥1000),greater damping(0.4＜α＜0.6)was required.This is understandable since the rate of chemical reaction depends on the Damkohler number which,in turn,controls the stiffness of the problem.

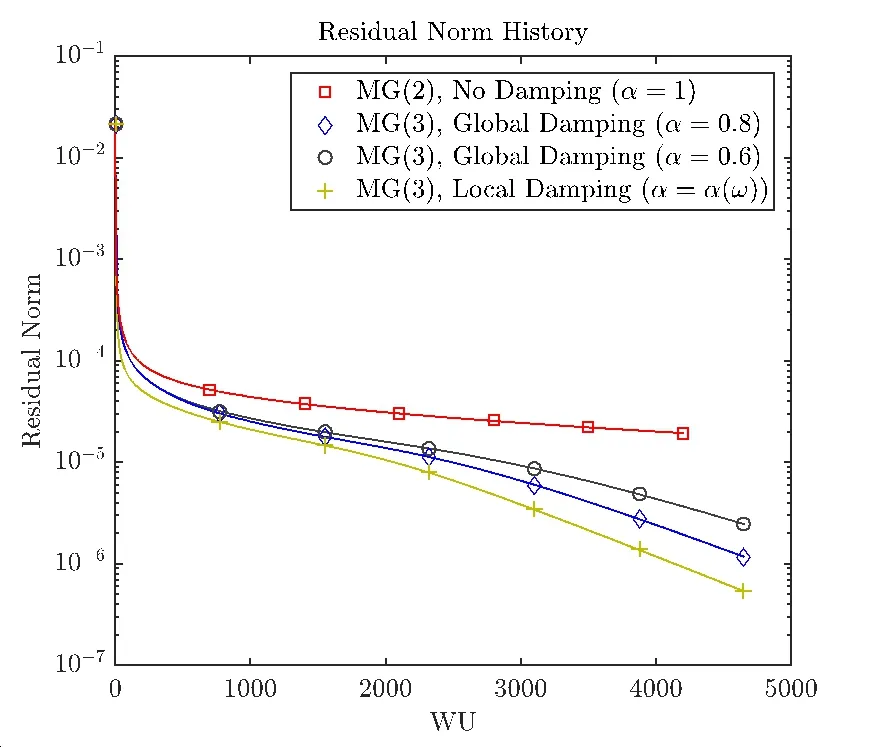
Figure 7:Comparison between the convergence histories using multigrid with different error damping methods;Data as in text but D=100.

Figure 8:Comparison between convergence histories for different values of the under-relaxation parameter;data as in text.

In Figure 8 the effect of the under-relaxation parameter,w(see Eq.(14)),on evolution of convergence is drawn.For this problem the optimal value was found to be 0.9,both for multigrid and for a single grid computation.The discrepancy between this value and that commonly used for the Jacobi method with multigrid in linear problems(w=2/3)is presumably due to the strong influence of the nonlinear chemical source terms.We have already mentioned the influence of the number of degrees of grid coarsening on convergence.In Figure 9 this theme is developed in further detail.It can be observed that additional levels of coarsening are extremely effective in accelerating the reduction rate of errors,as demonstrated in the improved iterative convergence rates of three-level multigrid(MG(3))over that of two-level multigrid(MG(2))and single-grid methods.The advantage in employing a multigrid method is clearly seen for this set of parameters.While the MG(3)method yields a reduction of 10 orders of magnitude of the discrete residual in roughly 4500 WU,the single-grid method is only able to reduce the residual by two orders of magnitude in an equivalent computational effort(similar number of WU).Furthermore,an acceleration of roughly six(6!)times is obtained in the computational time required to obtain the same level of convergence(residual norm of 10−4)by using the MG(3)method,with respect to the single-grid method.

Figure 9:Comparison between convergence histories for single and multigrid solution;data as in text.

However,numerical instabilities and degraded performance are likely to appear on coarse grid levels when the non-linear chemical source terms are dominant,due to the inability to properly represent non-smooth functions with rapid spatial variance on coarse meshes.

In Fig.10 the iterative convergence history is drawn for different Damkohler numbers for use of a single grid and multigrid with two grid levels.It is evident that the rate of convergence is hardly influenced by the Damkohler number.However,Fig.11 demonstrates that when more than two levels are utilized for the multigrid solution sensitivity to the Damkohler number does exhibit itself.

Figure 10:Comparison between convergence histories for single and multigrid(two level)solution for various Damkohler numbers;data as in text.

In Fig.11 it can be seen that for values of the Damkohler number exceeding 1000,monotonic convergence is slowed down when three grid levels are used,and the solution stalls.Since the value of the Damkohler number directly controls the chemical production source term it thereby controls the non-linearity of the problem and the error smoothness which deteriorates when the local chemical reaction becomes dominant.In order to handle this strong non-linearity an extremely significant reduction(α≈0.4)of the error transferred to the third mesh in the hierarchy is required so that no significant contribution to acceleration is achieved by including this mesh in the multigrid hierarchy.Consequently,two-level multigrid(MG(2))and three-level multigrid(MG(3))cycles yield similar convergence rates for D＞1000.

Figure 11:Comparison between convergence histories of multigrid(three level)solution for various Damkohler numbers;data as in text.

5.3 Results

In view of the aforementioned findings all results to be shown henceforth were obtained using a two-level MG.In addition,two pre-smoothing(before grid coarsening)and one post-smoothing point Jacobi iterations were employed on all multigrid levels,except for the coarsest level where 2 iterations were performed.As mentioned in section 4.1 convergence was measured using Eq.(15)and a criterion of 10−6The value of the relaxation parameter for Jacobi iterations was 0.9 and the global damping parameter for MG was 0.8 forD＜1000 and 0.4 forD≥1000(It should be noted that the above parameters were also utilized when producing Fig.6).

In Figure 12 a typical flame structure is illustrated forD=80.The colors relate to the reaction rate whereas the contours are those of the temperature.The mixture fraction is unity so that the flame is symmetric about the x-axis.The most intensive reaction rate is found in the partially premixed root of the flame structure and the characteristic trailing diffusion flame between the fuel and oxidant streams is clear.In Figures 13 and 14 the chemical Damkohler number is 450 and 1000,respectively.The flame structures are qualitatively similar to that of Figure 12 as the mixture strength is unity,but the intensity of the premixed reaction zone increases quite dramatically withD,as can be seen by comparing the different color scaling in these three figures.It is this increased intensity that necessitates a stronger global damping parameter,although there does not,at present,seem to be a simple analytical way to automate the choice of α in view of the problems’nonlinearity.The influence of the mixture strength on the edge flame structure is clearly captured in Figures 15 and 16.A value of φ less than unity is indicative of a fuel lean situation whereas a value greater than one relates to a fuel rich case.In Figure 15 the former case is considered for φ=0.1.The entire reaction zone(both the partially premixed and diffusion flame sections)is displaced into the region above the liney=0 due to the excess of oxidant.Conversely,for φ=5 the fuel is in excess and the flame region is stabilized belowy=0 in the lean oxidant stream(Figure16).It is interesting to note that for both these non-symmetric flames a section of the flame is established above/below the splitter plate itself.

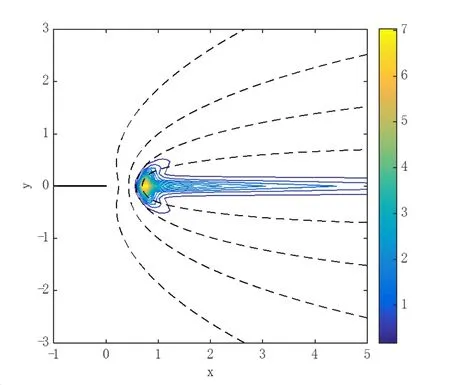
Figure 12:Typical flame structure illustrated by reaction rate(colors)and temperature contours;Data:φ =1;D=80;b=10−4.

6 Conclusions

Figure 13:Typical flame structure illustrated by reaction rate(colors)and temperature contours;Data:φ =1;D=450;b=10−4.

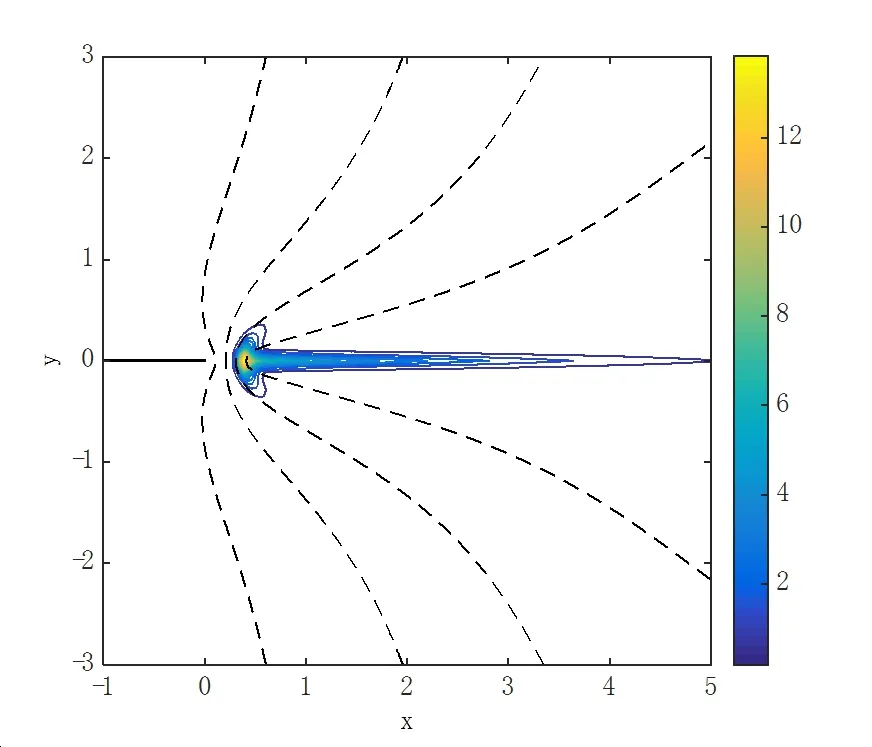
Figure 14:Typical flame structure illustrated by reaction rate(colors)and temperature contours;Data:φ =1;D=1000;b=10−4.

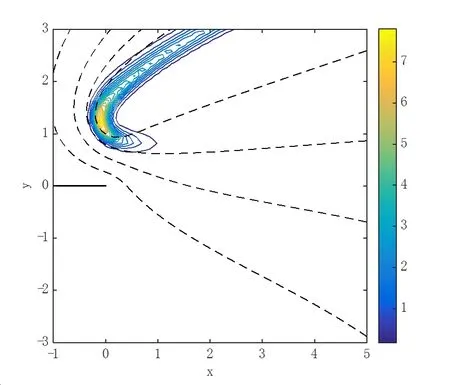
Figure 15:Typical flame structure illustrated by reaction rate(colors)and temperature contours;Data:φ =0.1;D=100;b=10−4.

Figure 16:Typical flame structure illustrated by reaction rate(colors)and temperature contours;Data:φ =5;D=100;b=10−4.

Application of multigrid acceleration to the solution of the equations describing the laminar edge flame formed in the mixing layer of two initially separated streams of fuel and oxidant has been described.The aim was to evaluate the performance of the method in the context of the iterative solution of the central difference finite difference scheme approximating the governing energy and species mass fraction conservation equations the latter being divorced from variable flow field and turbulence effects.The multigrid method was found to be extremely efficient and significantly improved the iterative convergence relative to that of a single grid method.For low to moderate chemical Damkohler numbers,acceleration factors of up to six(6!)times were recorded in the computational time required to obtain iterative convergence with the multigrid method,over that required with the single-grid method to obtain the same level of convergence.Moreover,monotonic convergence was obtained with the multigrid method in cases where the convergence of the single-grid method stalled.However,for large chemical Damkohler numbers of more than a thousand(i.e.very small characteristic chemical reaction times)and three levels of grid refinement the advantage of application of the multigrid method was seriously degraded due to the necessity to dampen errors stemming from the highly nonlinear chemical source terms on coarse grid levels of the multigrid hierarchy.This reduced performance may be attributed to the following.In the context of a global chemical kinetic scheme large Damkohler numbers can be viewed as expressing the flame surface as being an infinitesimally thin interface between fuel and oxidant with its attendant numerical difficulties.Use of a more detailed realistic chemical kinetic scheme may enable flame"thickening"(as found equivalently for lower Damkohler numbers)and thereby alleviate the aforementioned problem.The conclusions of the current study serve to highlight the tremendous potential of the multigrid method as well as its deficiencies.The critical dependence of the error damping parameter on the Damkohler number remains a moot point that warrants further investigation.The preliminary experience obtained through the study described here points to the need to conduct further research into creating a more robust,and,if possible,stabilization parameter-free,multigrid technique for dealing with the special numerical challenges that partial and non-premixed combustion present.

Acknowledgement:JBG thanks the Lady Davis Chair in Aerospace Engineering for partial support of this work.

Bellucci,V.;Bruno,C.(2001):Incompressible Flows with Combustion Simulated by a Preconditioning Method Using Multigrid Acceleration and MUSCL Reconstruction.International Journal for Numerical Methods in Fluids,vol.36,no.6,pp.619–637.

Brandt,A.(1977):Multi-level Adaptive Solutions to Boundary-Value Problems.Mathematics of Computation,vol.31,no.138,pp.333–390.

Brandt,A.(1998):Barriers to Achieving Textbook Multigrid Efficiency(TME)in CFD,Tech.Rep.ICASE Interim Report No.32,Institute for Computer Applications in Science and Engineering,NASA Langley Research Center.

Briggs,W.L.;McCormick,S.F.(2000):A Multigrid Tutorial,Society for Industrial Mathematics.

Bussing,T.R.A.(1985):A Finite Volume Method for the Navier-Stokes Equations with Finite Rate Chemistry,PhD thesis,Massachusetts Institute of Technology,USA.

Edwards,J.R.(1996):An Implicit Multigrid Algorithm for Computing Hypersonic,Chemically Reacting Viscous Flows..Journal of Computational Physics,vol.123,no.1,pp.84–95.

Edwards,J.;Royt,C.(1998):Preconditioned Multigrid Methods for Two-Dimensional Combustion Calculations at all Speeds.AIAA Journal,vol.36,no.2,pp.185-192.

Gear,C.W.(1971):Numerical Initial Value Problems in Ordinary Differential Equations,Prentice Hall PTR,Upper Saddle River,NJ,USA.

Gerlinger,P.;Mobus,H.;Bruggemann,D.(2001):AnImplicit Multigrid Method for Turbulent Combustion.Journal of Computational Physics,vol.167,no.2,pp.247–276.

Gerlinger,P.(2005):An Evaluation of Multigrid Methods for the Simulation of Turbulent Combustion.AIAA Paper 2005-4869,17th AIAA Computational Fluid Dynamics Conference,Toronto,Ontario,Canada.

Kim,S.;Kim,C.;Rho,O.(2001):Multigrid Algorithm for Computing Hypersonic,Chemically Reacting Flows.Journal of Spacecraft and Rockets,vol.38,pp.865–874.

Kurdyumov,V.N.;Matalon,M.(2004):Dynamics of an Edge Flame in a Mixing Layer.Combustion and Flame,vol.139,pp.329-339.

Law,C.K.(2006):Combustion Physics,Cambridge University Press,New York,NY,USA.

Lomax,H.;Pulliam,T.H.;Zingg,D.W.(2001):Fundamentals of Computational Fluid Dynamics,Springer Berlin,2001.

Mor-Yossef,Y.;Levy,Y.(2006):Unconditionally Positive Implicit Procedure for Two Equation Turbulence Models:Application to k–ω Turbulence Models.Journal of Computational Physics,vol.220,no.1,pp.88–108.

Mor-Yossef,Y.;Levy,Y.(2007):Designing a Positive Second-Order Implicit Time Integration Procedure for Unsteady Turbulent Flows.Computer Methods in Applied Mechanics and Engineering,vol.196,no.41-44,pp.4196–4206.

Mor-Yossef,Y.;Levy,Y.(2009):The Unconditionally Positive-Convergent Implicit Time Integration Scheme for Two-Equation Turbulence Models:Revisited.Computers&Fluids,vol.38,no.10,pp.1984–1994.

Sheffer,S.G.;Jameson,A.;Martinelli,L.(1998):An Efficient Multigrid Algorithm for Compressible Reactive Flows.Journal of Computational Physics,vol.144,pp.484–516.

Slomski,J.;Anderson,J.;Gorski,J.(1990):Effectiveness of Multigrid in Accelerating Convergence of Multidimensional Flows in Chemical Nonequilibrium.AIAA Paper 90-1575,AIAA 21stFluid Dynamics,Plasma Dynamics and Lasers Conference,Seattle,Wa.,USA.

Trottenberg,U.;Oosterlee,C.W.;Schuller,A.(2001):Multigrid Methods,San Diego:Academic Press.

Wasserman,M.;Mor-Yossef,Y.;Yavneh,I.;Greenberg,J.B.(2010):A Robust Implicit Multigrid Method for RANS Equations with Two-Equation Turbulence Models.Journal of Computational Physics,vol.229,pp.5820-5842.

Wasserman,M.(2014):Multigrid Acceleration of Turbulent Reacting Flow Simulations,PhD Thesis,Faculty of Aerospace Engineering,Technion–Institute of Technology,Haifa,Israel.

Williams,F.A.(1985):Combustion Theory,The Benjamin/Cummings Publishing Co.,Inc.Menlo Park,CA,USA.

Yavneh,I.(2006):Why multigrid methods are so efficient.Computing in Science and Engineering,vol.8,no.6,pp.12–22.