Efficient Load-balancing Scheme for Multi-agent Simulation Systems

K.Kuramoto,M.Furuichiand K.Kakuda

1 Introduction and related work

Recently,computer simulation has become an indispensable technology in various fields such as engineering,medical science[Caudill and Lawson(2013)],car traffic analysis[Yoshimura(2006);Fujii,Yoshimura and Seki(2010)],analyzing evacuation from a building[Kuramoto and Furuichi(2012)],and defense training[Wittman and Harrison(2001)].As the scale of simulation becomes large,computing efficiency becomes important.

A load-balancing method is an important issue in high performance computing.Studies on them can be classified as shown in Fig.1.

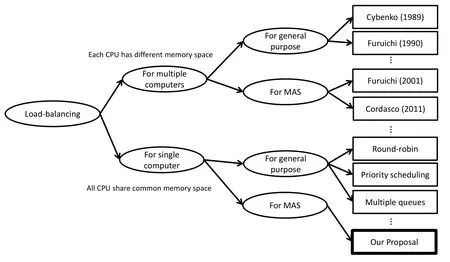
Figure 1:Taxonomy of load-balancing schemes.

In the field of operating systems,efficient methods for scheduling jobs on a CPU to derive the best performance have been studied and used for years[Tanenbaum(2008)].However,since operating systems are for general purposes,the dynamic behavior of applications can be used for load-balancing on a number of processors,cores,and GPUs.Therefore,the following schemes have been studied.

Classic methods have used one or more load balancers in a system to allocate jobs to processors to derive better performance[Cybenko(1989);Furuichi,Taki and Ichiyoshi(1990);Watts and Taylor(1998)].

Since multi-agent simulation(MAS)is a common application for computers,there are a number of job distribution studies for it.In the late 1990s,the United States Department of Defense developed a standard called High Level Architecture(HLA)for modeling and simulation,which became an international standard(IEEE std 1516).HLA is designed for distributed simulation,and it can work efficiently on multiple computers by balancing agent workloads.HLA is implemented as middleware with application program interfaces,but its basic functions do not include functions for load-balancing,and developers must employ their own schemes for the application.A scheme for such situation is Space Time Object Model,an object management scheme of moving agents for efficient processing on distributed computers[Furuichi,Ozaki,Abe,Nakajima and Tanaka(2000);Furuichi,Ozaki,Matsukawa,and Iwase(2001)].Agent management,deciding which computer should own an agent,is still the key technique for load-balancing on multiple computers[Cordasco,De Chiara and Scarano(2011)].

As stated above,the research trend of load-balancing in the MAS field tends to focus on distributed systems.However,there are few studies on the efficiency of MAS framework on a single computer with multiple cores.Load-balancing methodology on a single computer differs from that on distributed systems.For MAS on distributed systems,the important point of job distribution is reduction of information exchange between agents on other computers.In contrast,in the case of MAS on a single computer,all agents share the same physical memory,and information exchange among agents is not a serious efficiency problem.The primary issues of load-balancing on a single computer are reducing job-fetching time and evening the workload among all threads.

Although it is certain that performance efficiency on distributed systems is obviously important in conducting very large-scale simulations,the performance on a single computer also deserves attention.Nowadays,powerful desktop computers can conduct simulations with a large number of agents,and many simulation users run their simulations by a single PC on their desktop.

Therefore,we propose a load-balancing scheme that focuses on MAS with heterogeneous agents that have various roles and broad workloads.

2 FUSE:a multi-agent framework

We have developed a multi-agent framework FUSE that focuses on hierarchical organization behaviors with a large number of agents to simulate a human organization[Kuramoto and Furuichi(2013)].It is a library-type framework for building MAS systems easily,and provides functions commonly required by multiagent systems such as agent management,message passing,and two-and threedimensional visualization.

Our first objective in developing FUSE was to simulate organized agents similar to a human organization;hence,FUSE contains functions for simulating the decision making of organization leaders.Furthermore,since the framework can operate thousands of agents and can set decision-making rules easily,the framework is used in our laboratory for various types of simulation.Some examples of MAS programs created using FUSE are shown in Fig.2.

One of the important functions of such a framework is a load-balancing mechanism,since recent computers have multiple cores,and efficient simulation execution requires efficient workload distribution to the computer’s threads.

In particular,FUSE deals with agents whose workloads can be very different depending on purpose of a framework.For example,in the case of simulating human behaviors in hierarchical organization,there is a significant difference between the workload of a top leader agent and that of an underling agent.

Figure 2:Simulation programs built using FUSE(Top:reaching a goal by co-op demonstration,Right:historical battle simulation,Left and Bottom:counter fire disaster simulation).

3 Proposed scheme

3.1 Underlying factors of the study

Since our algorithm is optimized for the MAS framework on a single computer,it has presuppositions and constraints.First,target jobs are usually various tasks,but they are all conducted by agents,and they are presumed to have workloads with time series relevance,since many of the agents exist for multiple simulation cycles.Accordingly,an agent’s workload can be estimated based on its status.Second,physical memory is shared by all threads on a single computer.Therefore,all threads can access the entire memory of a process evenly,and there is no cost in sharing information with agents on other threads.Third,in the case of time-steptype MAS,all agents have the same job priorities,and the number of jobs on the time-step cycle is fixed in advance.Given these factors,conditions for providing jobs are relatively simple compared with providing general OS processes.

A typical agent job distribution mechanism on a single computer is shown in Fig.3.The algorithm allocates agent jobs to threads cyclically,with all threads having nearly the same number of agent jobs.After jobs are allocated,the threads are executed.In this figure,Thread 1 is the critical thread,and other threads must wait for it.

An appropriate load-balancing method is required to solve the inefficiency problem of CPU resource.If programmers can set accurate values for agents’workload in program code manually,the task becomes very easy.However,in reality,it is difficult to estimate an agent’s workload in advance,and the usability of the framework deteriorates substantially if simulation developers are required to predict their agent’s workload.Therefore,workload estimation must be implicit for programmers.

Figure 3:Simple job distribution.

3.2 Estimating workload of agent-job

Focusing on MAS,we built on a hypothesis that an agent’s job workload does not change frequently.In other words,we regarded an agent job’s workload on a timestep cycle to be close to what it was on the previous cycle.Therefore,if an agent workload on the current cycle is sufficiently similar to that of the previous cycle,it is possible to achieve load-balancing of threads using information of previous workload.

Fig.4 illustrates this method.At first,agent jobs are sorted in descending order of their workloads on the previous cycle,and then jobs are allocated one by one to the thread that has the minimum estimated workload at that time.Sorting is significantly important,since the workload of the last-fetched agent directly affects the thread’s waiting time.The utility of sorting for performance more than compensates for its computing time.

Consequently,estimated workloads of threads are expected to be nearly equal,improving CPU usage efficiency.

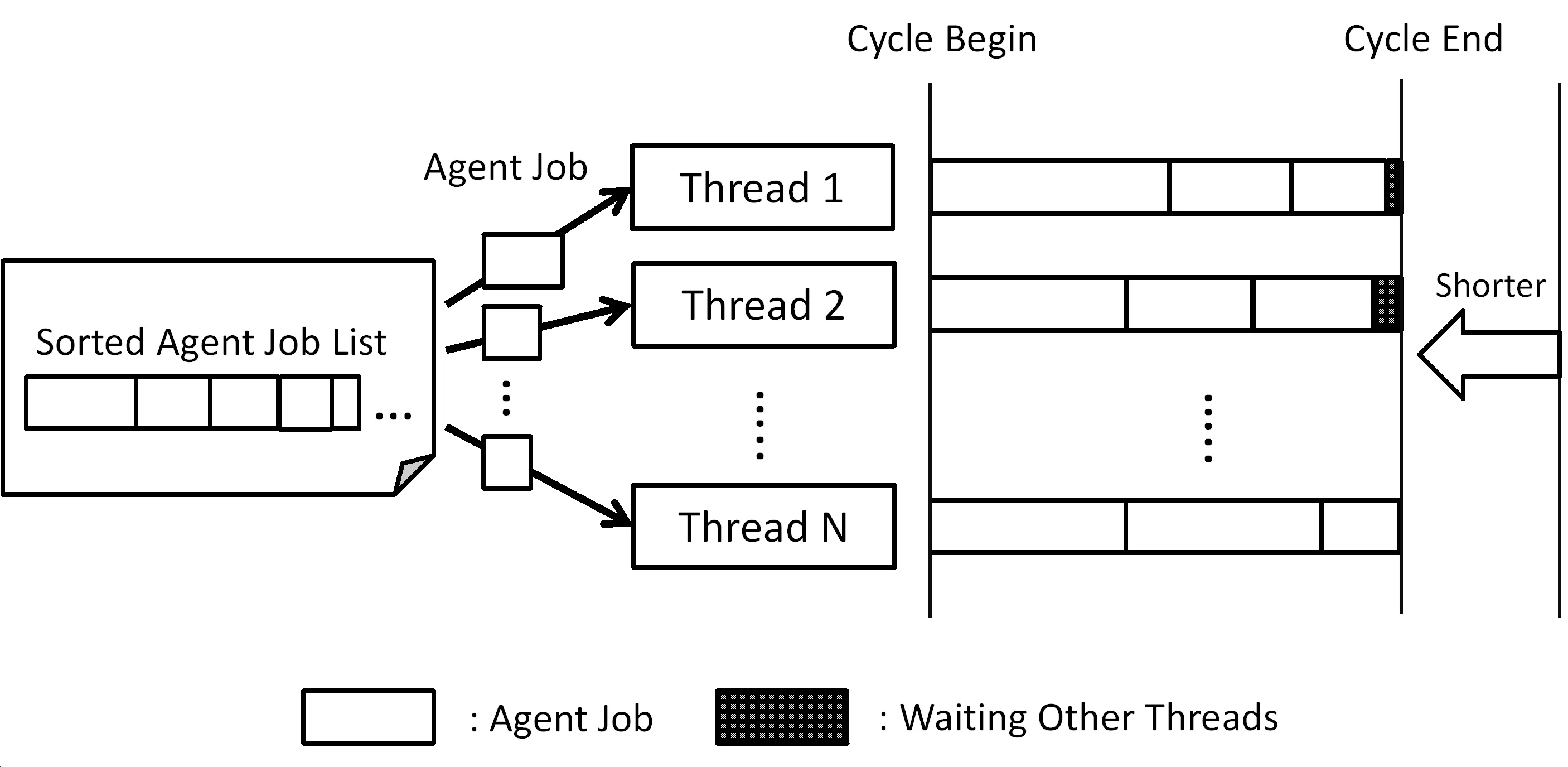
Figure 4:Job distribution using previous workload information.

3.3 Dynamic distribution

The above methods provide jobs to threads statically.If all of the estimated workloads are perfectly correct,static job distribution is an effective manner of achieving load-balancing.However,estimation from an agent’s previous workload is not always accurate,since an agent’s job is not the same on each time-step cycle.Even if our hypothesis is correct ideally,and an agent’s job workload changes very slightly,it is impossible to eliminate the error between the estimated and actual workloads.Therefore,a robust mechanism against error is required,and we propose dynamic job distribution as the solution.In this algorithm,each thread requires a new job after every job execution,and an agent manager allocates jobs to threads.

An advantage of dynamic distribution is robustness against estimation error.In the other hand,static algorithm causes waiting of threads for others,since assignment of jobs has been fixed in advance and there is no opportunity to restore job distribution.In contrast,idle threads always require jobs in a dynamic algorithm,reducing the idling time.Since agent jobs are sorted,workloads of jobs executed on the previous time-step cycle might be small.Consequently,gaps of processing time in each thread become very small(Fig.5).

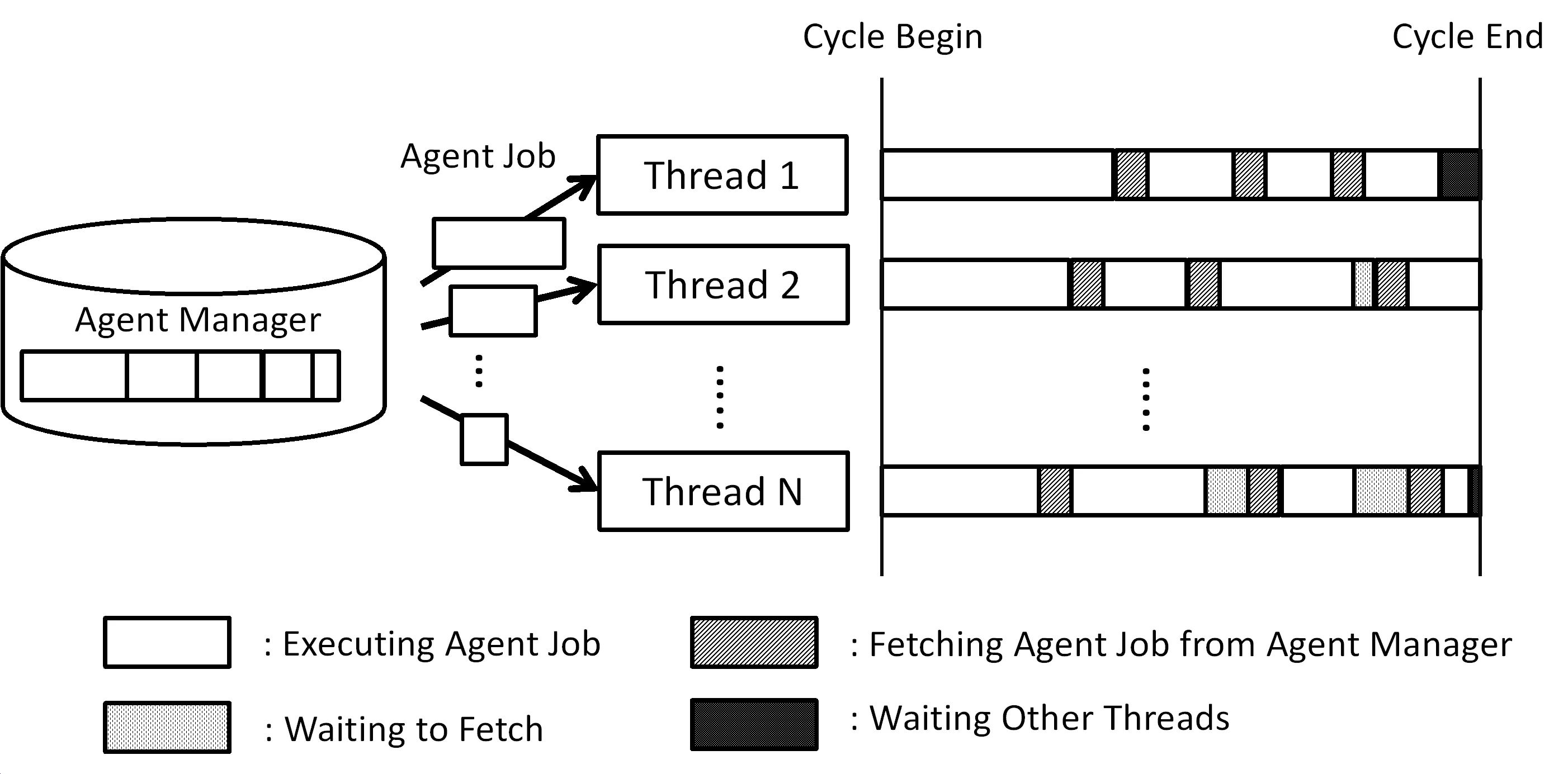
Figure 5:Dynamic individual job distribution

Although a dynamic distribution method looks more appropriate than a static one,it has problems in the job-fetching phase.Since a static method allocates jobs to threads before beginning parallel processing,thread safety is not an issue.

In contrast,in the dynamic method each thread requires jobs with parallel processing,and threads can try to access the agent manager simultaneously.This creates a need for a locking mechanism to avoid job-fetching collision.However,a lockunlock mechanism for job fetching can degrade performance.

We test two types of method in this paper,fetching jobs individually and fetching jobs as clusters to reduce the number of fetching,as illustrated in Fig.6.We expect the clustering to reduce fetching time;however it may cause to increase thread waiting time as a result of the unit size of jobs.

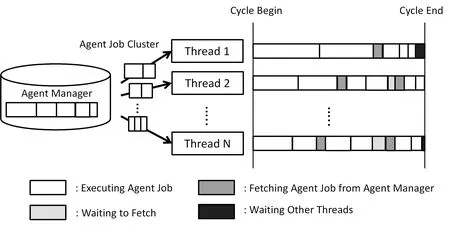
Figure 6:Dynamic clustered job distribution

3.4 Details of the algorithm

The algorithm proposed in this paper has two primary parts,sorting jobs using previous workloads and gathering jobs into clusters.

As mentioned above,agent jobs must be sorted in descending order to reduce workload gaps of threads,and the individual job distribution method follows this principle.Furthermore,the principle must be adapted to the job clustering method.Therefore,we have to determine two parameters,initial-ratio and reduce-ratio,in the algorithm.

Initial-ratio is the ratio of the first job cluster size to the total agents’workload size.Reduce-ratio is the ratio of cluster size reduction.Consequently,cluster size follows a geometric progression.If both initial-ratio and reduce-ratio are relatively large,then the number of fetching processes becomes small,but job cluster size tends to increase,and workload gaps in each thread can become wide.If these ratios are small,then keeping thread’s workloads equal becomes easy,and the number of fetching increases.

We consider a normalized agent workloadW.

In equation(1),Ris the reduce-ratio andIis the initial-ratio.The normalized workloadWcan be regarded as the number of threadsN.WhenNapproaches infinity,we define the relationship between these ratios as follows:

The equations(2)and(3)define the relationship between initial-ratio and reduceratio.Initial-ratio must be given to compute the cluster size.Generally,if the agent workloads are nearly fixed,and estimation succeeds every time,a large initial-ratio might make the simulation efficient,because the number of fetches is reduced.Conversely,if agent workloads are not stable,then estimation often creates large errors;it is risky to adopt a large initial-ratio in such a situation,because of the possibility of increasing waiting time.

However,since it is difficult to decide the ratios in advance,we introduced an adaptive method.At the beginning of a simulation,initial-ratio is always set to 0.5.Then,when the simulation cycle is an odd number,temporal initial-ratio is reduced by a small valuediff,and conversely,if the cycle is an even number,the ratio is increased bydiff.Next,an agent manager considers the past 10 cycle times to determine whether the next initial-ratio is to be increased or decreased.

As shown in Fig.7,the agent manager counts the number of wins in bigger and smaller cases of past cycles.If the number of wins in bigger cases is greater than in smaller cases,then the manager increases initial-ratio.If the number in smaller cases is greater than in bigger cases,then the manager reduces initial-ratio.In either case,the speed of changing the actual initial-ratio is much less than thediffvalue.Since we use 10 past cycle data,initial-ratio is fixed in the 10 cycles,and we apply the adaptive method from the 11th cycle.

Figure 7:Initial-ratio deciding process.

4 Performance experiments and results

In this section,we explain the experiments for evaluating our algorithm and present its results.We tested four algorithms,static cyclic,static with estimation,dynamic estimated individually,and dynamic estimated with clusters.All of our program code for the experiments is written in Java which is the language of developing FUSE.

In our experiments,we test our method on primitive agents with simple calculation tasks initially.The result of the first experiment helps to discuss the algorithm logically,because the number of these test agents and workloads are controlled.Then,we exhibit the results of the algorithm on a practical MAS system with more than 1,000 agents that was developed for decision-making training of leaders.

4.1 Experiments on test environment

4.1.1 Condition of experiments

We test the proposed algorithm on a test program with primitive agents.These agents involve a task of simple calculation.In particular,we calculate the number π by placing a large number of random points and testing each point whether it is in a 1/4 circle or not.A computer specification of the experiment is shown in Tab.1.

The agent workloads are produced using a random function that follows the mathematical distribution shown in Fig.8,with its specification shown in Tab.2.We used the following two patterns for agent workload.

1.Agent workloads follow an exponential distribution.

2.Agent workloads generally follow an exponential distribution,but a small number of agents have extremely large workloads.

The second situation assumes the case that includes small numbers of special agents that have much bigger workloads than other agents.

4.1.2 Experimental results

We now show that results of the experiments.Fig.9 shows the relationship between number of threads and cycles per second for each algorithm.The horizontal and vertical axes represent the number of threads and cycles per second respectively.Bigger number is better for the cycles.

The values are the average outputs of 25 executions.The figure indicates that dynamic algorithms are superior to static algorithms,and estimation is efficient inboth of cases that dynamic and static.In addition,there is no significant difference between the two dynamic algorithms.

Table 1:Experimental Environment.

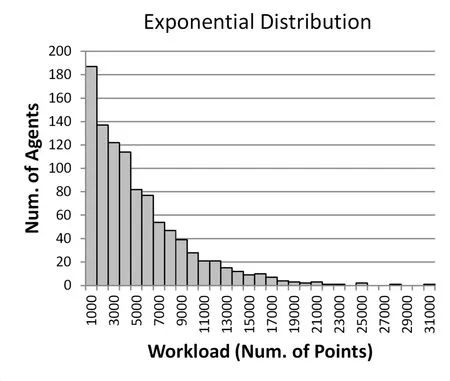
Figure 8:Agents’workload distribution.

Table 2:Experimental Condition.

Subsequently,we tested cases in which there are agents with extremely large workloads.We changed 10 normal agents to big agents and prepared four workload patterns.In all of the patterns,all big agents have same size of workloads.The patterns are 50k,250k,500k,and 1,000k points for pseudo-simulation.

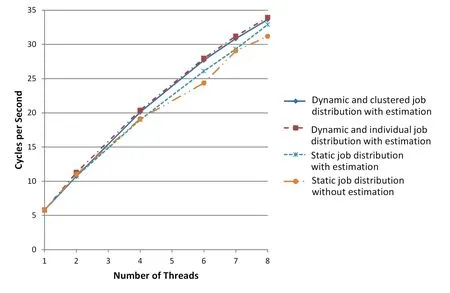
Figure9:Relationship between simulation cycles per second and number of threads(1/3).

The results are shown in Fig.10.The performance tendency shows that as the difference in workload among agents’increases,the difference of performance widens between estimated and non-estimated algorithms.

If these big agents are gathered in one or two threads,the threads’workloads become too large,and other threads must wait for them.In such a situation,workload estimation becomes more important than in the case of flatter workloads.Conversely,the difference between estimated algorithms is almost independent of the workload size of big agents.According to the results of the test program,it is proved that workload estimation and dynamic job distribution is efficient.However,those results are output of a test program,with each agent’s workload being very stable.Substantiating the usefulness of our proposed method requires testing on a practical simulation.

4.2 Experiments on practical simulation

We described experiments on primitive agents and the results in the previous section.In this section,we describe another set of experiments using a practical MAS system.

Figure 10:Relationship between simulation cycles per second and number of threads(2/3).

The MAS for these experiments is a simulation developed for decision-making training of leaders containing heterogeneous agents with various workloads.The simulation system has an autonomous mode on which we run the simulation during the experiments.The appearance of the simulation is shown in Fig.11 and 12.

The simulation models a fire extinguishing operation in an urban area,with its agents’roles shown in Tab.3.H.Q.,leader,fire fighter,and evacuee simulate human beings and can move and send information.Fire is a very simple agent whose role is to burn a structure at the specified position and spread to neighboring cells.

The H.Q.and leader agents command subordinates,with workloads much heavier than those of fire fighter,evacuee,and fire.In addition,in contrast to the test program,each agent’s workload changes depending on the situation around the agent.Testing our algorithm on such a practical simulation environment provides an appropriate examination of the effectiveness of workload estimation.

Figure 11:Screenshot of the simulation program.

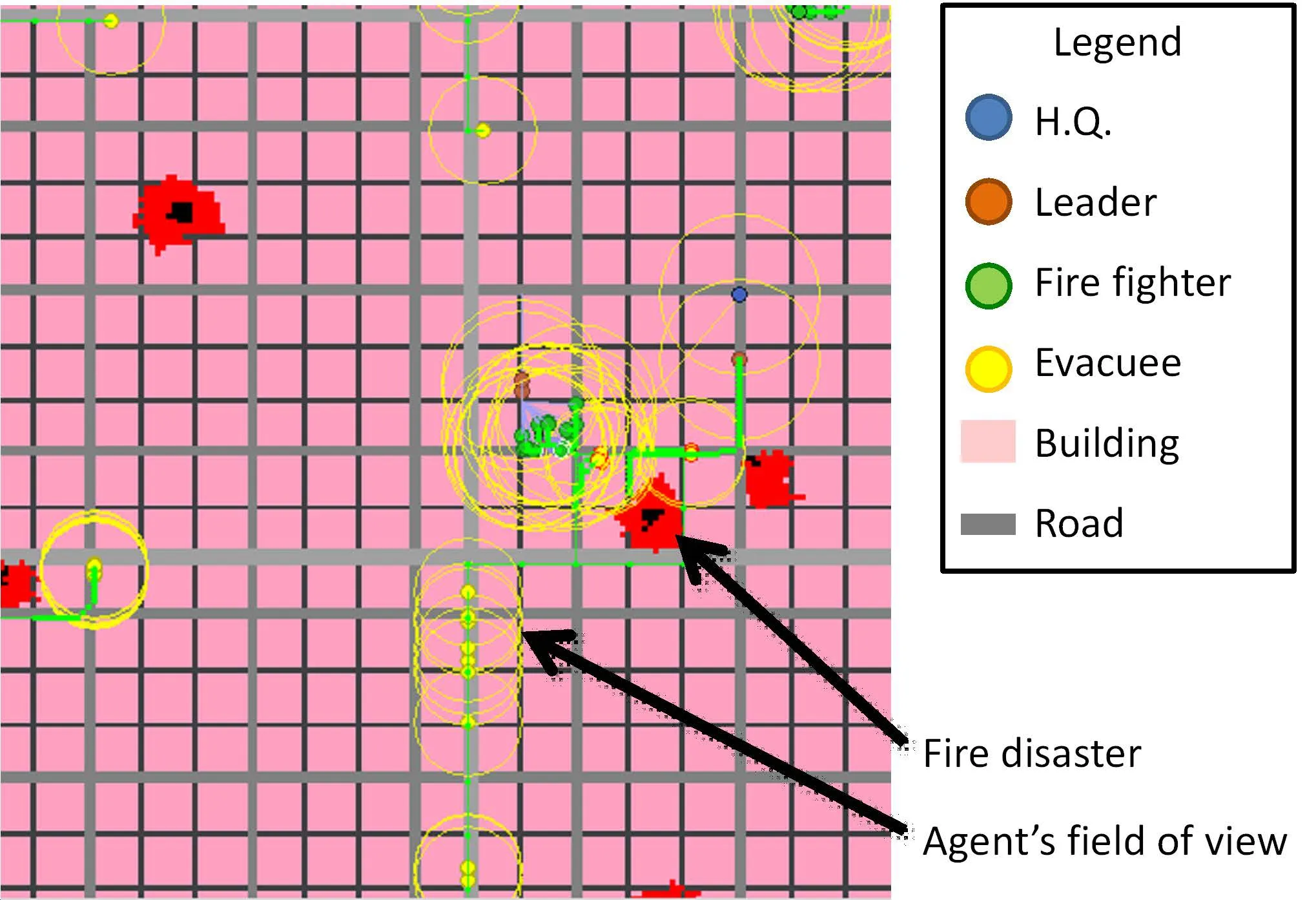
Figure 12:Instructions to the simulation’s screen.

The results of the experiments are shown in Fig.13,each value being the average of 25 executions.They are similar to those of the test program and show that estimation of workload is effective even in a practical situation.Similarly to the experiments with the test program,estimation works to improve simulation performance and output,with dynamic algorithms being superior to static algorithms.In addition,the results are similar to that of individual and clustered fetching which do not differ significantly.

In conclusion,our load-balancing scheme using estimation can improve simulation performance in practical conditions.The important points are using estimation and allocating jobs dynamically.Although we expected a significant effect from clustering,the experiments did not confirm that expectation.

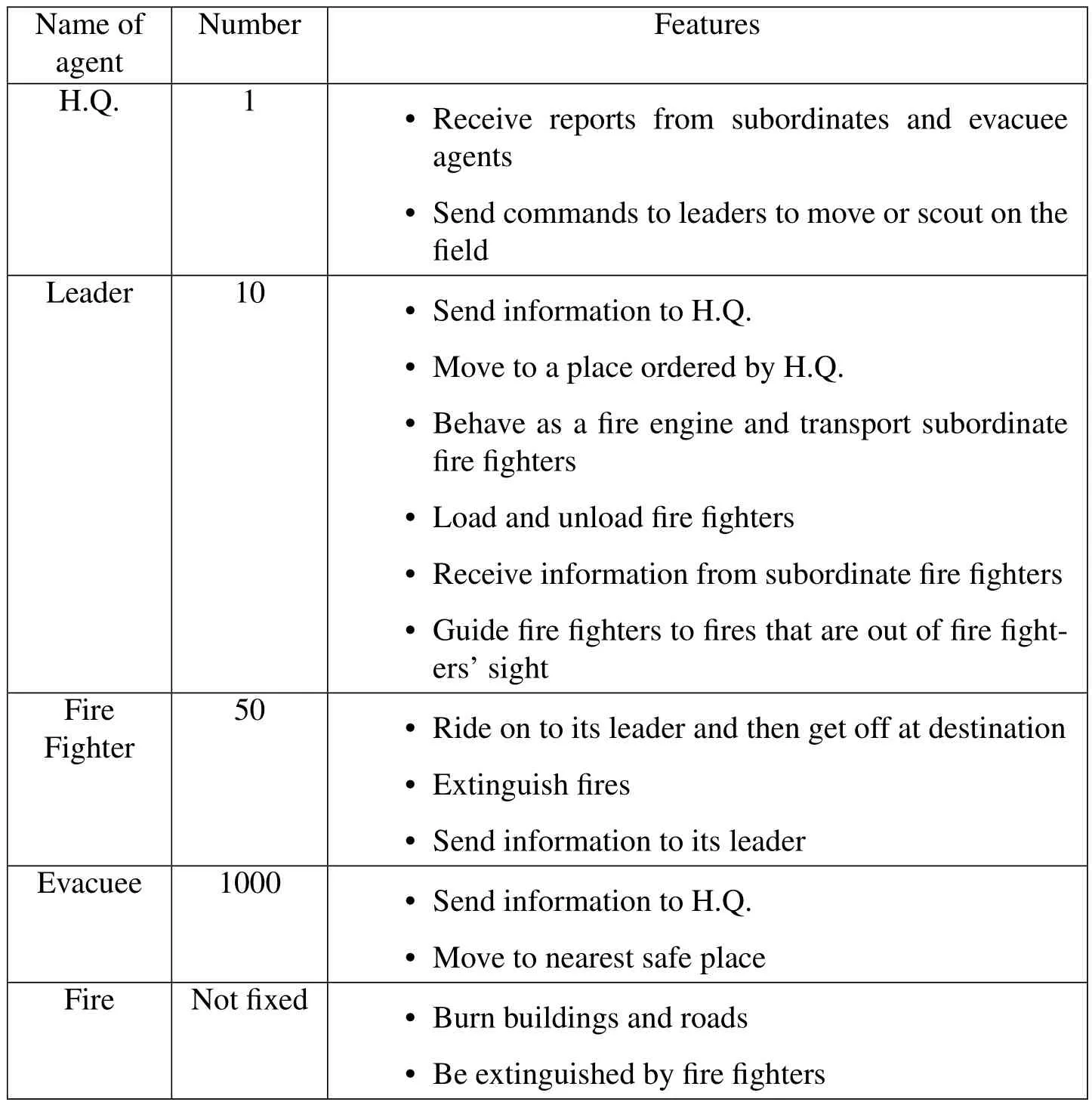
Table 3:Types of Simulation Agents.

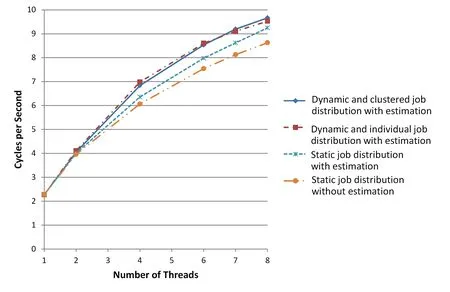
Figure 13:Relationship between simulation cycles per second and number of threads(3/3).

5 Discussion

We elucidated the advantage of using workload estimation and dynamic load-balancing to improve performance of MAS.Since our algorithm is simple,using only previous workload of each agent,integration into existent simulation framework is easy and places no extra load on simulation developers.It is disappointing that the clustering process shows no significant effect.It is suspected that our estimation of job fetching time might be excessive for the conditions,and number of CPU cores of the experimental computer might be too little to utilize clustering part of our scheme.We believe that the matter deserves further investigation.

6 Conclusion and future work

We described a load-balancing scheme specialized for the MAS framework.The method estimates next workload from previous workload and performs dynamic load-balancing.We demonstrated its effectiveness through experiments.In first experiments,we evaluated our scheme on the test program that is given a simple task,and then we confirmed that workload estimation by using previous workload each agent works effectively.

In second experiments,we adopted more practical and complicated MAS application program that includes huge number and multiple kinds of agents.In this program,each of agents has its own role and makes decision depending on each situation.As a result,workloads of agents are changing because their situations also change.In the case of the experiments,our scheme showed superior results and was confirmed its effectiveness on the practical MAS application.

Our next plan is to introduce our scheme on larger multi-core systems which expected to show the effectiveness of the combination of workload estimation and job clustering algorithm.Moreover,combining our method with various types of distributed systems is also our future work.Our proposed method focuses on processing on a single computer,and there are number of load-balancing methods for multiple networked computers.This will create a synergetic effect and will be linked to developing new resource-efficient methods for distributed MAS systems.

Caudill,L;Lawson,B.(2013):A Hybrid Agent-based and Differential Equations Model for Simulating Antibiotic Resistance in a Hospital Ward.Proceedings of the 2013 Winter Simulation Conference,pp.1431-1442.

Cordasco,G.;De Chiara,R.;Scarano,V.(2011):Distributed Load Balancing for Parallel Agent-Based Simulations.Proceedings of Parallel,Distributed and Network-Based Processing(PDP),19th Euromicro International Conference,pp.62–69.

Cybenko,G.(1989):Dynamic Load Balancing for Distributed Memory Multiprocessors.Journal of Parallel and Distributed Computing,vol.7,Issue 2,pp.279–301.

Fujii,H.;Yoshimura,S.;Seki,K.(2010):Multi-agent Based Traffic Simulation at Merging Section Using Coordinative Behavior Model.CMES,vol.63,no.3,pp.265-282.

Furuichi,M;Taki,K;Ichiyoshi,N.(1990):Multi-Level Load Balancing Scheme for OR-Parallel Exhaustive Search Programs on the Multi-PSI.ACM SIGPLAN,vol.25 Issue 3,pp.50–59.

Furuichi,M.;Ozaki,A.;Abe,K.;Nakajima,K.;Tanaka,H.(2000):A Space-Time Object Model–An Object Oriented Model for Parallel and Distributed Simulation.IEICE transactions on information and systems,vol.E83-D,no.4.

Furuichi,M.;Ozaki,A.;Matsukawa,H.;Iwase,T(2001):Design and Implementation of Parallel and Distributed Simulation Development and Runtime Support Environment Based on HLA and Its Evaluation.IEICE transactions D-I,vol.J84,no.12,pp.1610–1622.

Kuramoto,K.;Furuichi,M.(2012):A Design and Preliminary Evaluation of Hierarchical Organizational Behavior Modeling Architecture.Proceedings of JSST2012 International Conference on Simulation Technology,RS1-7.

Kuramoto,K.;Furuichi,M.(2013):FUSE:A Multi-agent Simulation Environment.Proceedings of the 2013 Winter Simulation Conference,pp.3982–3983.

Li,T.;Baumberger,D;Koufaty,D.A.;Hahn,S.(2008):Efficient Operating System Scheduling for Performance-asymmetric Multi-core Architectures,SC’07 Proceedings of the 2007 ACM/IEEE conference on Supercomputing,Article No.53.

Tanenbaum,A.(2008):Modern Operating System third edition,Pearson Prentice Hall.

Watts,J.;Taylor,S.(1998):A Practical Approach to Dynamic Load Balancing.Parallel and Distributed Systems,IEEE Transactions,vol.9,Issue 3,pp.235–248.

Wittman Jr;R.L.;Harrison,C.T.(2001):OneSAF:A Product Line Approach to Simulation Development.proceedings of Euro-Simulation Interoperability Workshop,01E-SIW-06.

Yoshimura,S.(2006):MATES:Multi-Agent based Traffic and Environment Simulator–Theory,Implementation and Practical Application.CMES,vol.11,no.1,pp.17-25.