适合16－QAM信号的盲均衡算法

张建平，熊建国，曾小玲

(重庆科创职业学院，重庆402160)

适合16－QAM信号的盲均衡算法

张建平，熊建国，曾小玲

(重庆科创职业学院，重庆402160)

提出并采用修正恒模算法(MCMA)和判决引导的最小均方算法(DD－LMS)联合均衡算法，对16－QAM系统接收端的码间干扰进行均衡。分析了联合均衡的技术的实现方式和切换门限，对四种不同的均衡算法进行了仿真实验。仿真结果表明，MCMA与DD－LMS联合均衡算法较之其它三种均衡算法，能够将剩余误差迭代得更小，而且可以有效地修复传输过程中产生的相位偏移。

修正恒模算法;判决引导的最小均方算法;盲均衡;联合均衡

在不断发展的通信领域，随着信息量的变大，需要不断提升信息的传输速率。而提升信息的传输速率，可以改善通信发送端和接收端的信号处理硬件和软件，或者通过采用更高的码制来提升信息传输速率。［1］以十六进制的正交幅度调制(16Quadrature Amplitude Modulation，16QAM)星座图为基础的调制方式，可以提供现代通信系统一个较高的码率，符合现代通信发展的需求。在接收端，为了消除码间干扰，采用均衡技术。

常用的常模算法(Constant Modulus Algorithm，CMA)算法是Godard提出的算法的其中一个特例，其基于输出信号的高统计量的盲均衡，对信号相位和幅度进行独立恢复，适用于存在载波偏移的通信系统。［2］由于CMA算法在很多信道中会存在相位偏转现象，故本文拟采用修正恒模算法(Modify Constant Modulus Algorithm，MCMA)对接收信号进行均衡处理，MCMA对信号的x轴和y轴分别进行误差计算和抽头系数更新，以修正由于多径效应引起的信号相位失真。

MCMA算法具有收敛性能高，均衡器计算复杂度低，结构简单等优点，可是该均衡算法收敛速度慢，剩余误差大。而同时，判决引导的最小均方算法(Decision－Directed Least－Mean Square，DD－LMS)可以有较低的剩余误差，但在均衡刚开始误差过大时，DD－LMS算法却有可能判决错误而造成剩余误差发散的结果，故不能直接使用DD－LMS算法进行均衡器的冷启动。［3］倘若仅仅使用上述的其中一种均衡算法，都大大制约了均衡器的效果，无法适应日益发展的通信信号处理要求，使得16QAM信号处理具有很大的局限性。

本文采用MCMA和DD－LMS算法进行联合盲均衡，以使得均衡器同时兼备均衡后误差收敛和均衡后剩余误差较小等优势。

一 均衡器通信系统模型

图1是通用的盲均衡通信系统模型，［4］其中x(n)是发送端发送的信息序列，h(n)是传输信道的信道相应，d(n)是信道中加入的噪声，y(n)是接收端所接收到的信息序列，w(n)是均衡器的抽头系数，z(n)是更新抽头系数时的均衡器输出信息序列，^x(n)是判决器输出的判决序列。

图1 均衡系统模型

由图1，通信系统的接收端输入序列y(n)可以表示为:

式中，表示卷积运算。

而均衡器输出信息序列z(n)可以表示为:

二 联合均衡算法

在联合均衡中，虽然确定了使用CMA/MCMA和DDLMS两种均衡算法，但是何时进行两种算法的切换却十分重要。因为切换得过早，CMA/MCMA尚未收敛，误码率过高而导致DD－LMS算法不能收敛，从而引起均衡器的发散和较高的误码率;而如果切换得过晚，则容易导致均衡器收敛的速度过慢，因此必须确定一个最优的切换门限时间。

盲均衡算法可分为补货和跟踪两种模式。CMA算法具有稳健的收敛性，可以用于均衡开始时使眼图张开，而DD－LMS算法可以用于均衡眼图张开后减小剩余误差。［5］

联合均衡的基本思想是在信道眼图还没张开的时候，使用CMA或者MCMA算法作为冷启动，通过一定次数的迭代，当误码率较低的时候，再切换到DD－LMS算法，使得剩余误差进一步减小。

通信系统中的16QAM星座图如图2，当CMA或者MCMA算法的剩余误差e(n)=z(n)(|z(n)|2－R2)没有收敛到眼图张开时，即剩余误差e(n)还没到达切换的门限值时，持续用CMA或者MCMA算法收敛，直到当判决使得眼图张开，大部分点都落在图2中的各个小圆圈内是，切换到DD－LMS算法，加快收敛，减小剩余误差。

此外，在均衡刚开始收敛迭代的前期，也有可能将迭代到图2的小圆圈中，但此时实际上眼图并未打开，并不符合DD－LMS算法的要求。所以，改进的算法中将在迭代开始时的前若干次禁止切换到DD－LMS算法。

设n(n)为信道高斯白噪声，方差为σ2，均值为0，那么通信系统的传输信号信噪比为:

式中，E［x(n)2］是发送端信号的功率。

设Rmax是16QAM信号发送信号星座图最外层的信号半径，那么可以由(1)式，推出噪声的标准差σ为:

那么，以在星座图上的星座点为圆心，而以σ为半径的圆内，为均衡器收敛之后的判决落点。因此，联合均衡算法可以以此为判决圆的切换门限圆环进行判决，如图2所示。

而同时，假设16QAM星座图的最小欧氏距离为d，那么为了满足判决算法的收敛性能，则收敛圆半径r的取值范围为:［6］

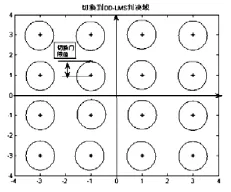
图2 切换到DD－LMS判决图

联合均衡时，其抽头系数迭代公式为:

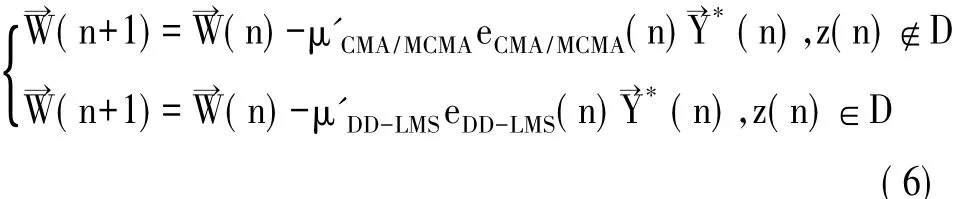
上式中，D为图2中小圆圈区域。

当误差的计算结果还没收敛到图2的小圆圈内的时候，使用(6)式中的第一条式子，使用CMA或者MCMA算法对误差进行迭代运算，当误差的计算结果收敛到了小圆圈之内时，使用第二条式子，通过DD－LMS算法对抽头系数进行更新。通过切换两种误差的计算公式，实现联合均衡。

三 仿真结果及分析

为了验证本文提出的联合均衡算法，对CMA算法，MCMA算法，CMA与DD－LMS联合均衡算法，和MCMA与DD－LMS联合均衡算法进行比较。比较各种均衡算法对信号的收敛作用及均衡星座图效果，并对各种均衡算法的剩余误差进行比对分析。

仿真参数设置如下:而信道响应函数h=［－0.005－0.004j 0.009+0.030j－0.024－0.104j 0.854+0.520j－0.218+0.273j 0.049－0.074j－0.019+0.020j］;噪声信号为高斯白噪声，信噪比SNR=30dB;CMA和MCMA算法的迭代步长μCMA/MCMA=0.00005;DD－LMS算法的迭代步长μDDLMS=0.005;信号序列长度N=5000;最小欧氏距离d=2;抽头系数阶数L=13;最小从CMA/MCMA算法进入DD－LMS算法次数Num=80;从CMA/MCMA算法进入DD－LMS算法误差门限值threshold=0.6。仿真效果图如下:

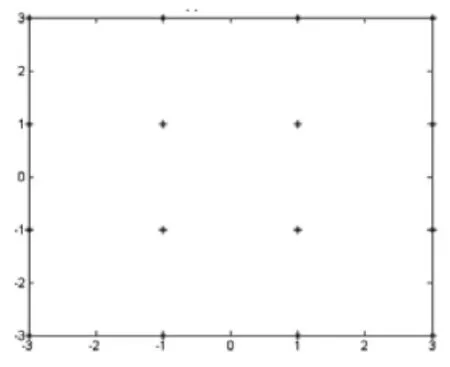
图3 16QAM编码调制星座图

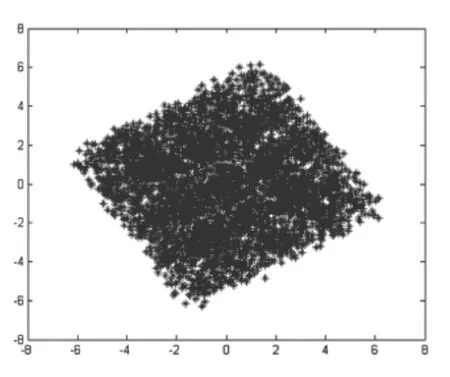
图4 信号经过信道传输后星座图

由图3，可以直观看到16QAM星座图为4*4个星座点，其中实验设置的最小欧氏距离为2。而图4是经过了信道函数变换，而且加入了信噪比SNR=30dB的接收端信号序列，可以看出，在接收端信号的变形非常大，误码率过大，所以必须经过均衡才能恢复发送端的信号。

1.均衡器输出星座图比较分析。

对CMA算法，MCMA算法，CMA与DD－LMS联合均衡算法，和MCMA与DD－LMS联合均衡算法进行仿真，得到的均衡器输出星座图如图5所示。

由图(a)经过了CMA算法的均衡，接收端的信号序列基本能够收敛，使得眼图张开，CMA算法具有收敛性能稳健，计算复杂度低的特点。但是，可以从图里直观看出，CMA算法均衡出来的信号序列还比较发散，而且有相位的偏移，这对后续的判决处理是非常不利的。从图(b)中看出，MCMA算法已经消除了CMA算法中的相位偏移问题，

分开估计使得误差的估计更小，而使得图(b)上的点要比图(a)的点更收敛。图(c)是CMA算法和DD－LMS算法联合均衡的效果图，将图(c)与图(a)进行对比，可以看出，通过了联合均衡，可以使16QAM均衡出来的星座点进一步收敛，使得剩余误差更小。但是，CMA和DD－LMS的联合均衡并没有解决相位偏转的问题，图(d)是采用MCMA和DD－LMS算法联合均衡得到的输出结果。在图(d)中，每个星座点都收敛得非常小，达到了以上各种均衡算法中最优的均衡效果。

图5 各算法均衡效果图

均衡仿真时，在CMA/MCMA切换为DD－LMS算法的门限设定中，使用了两个常量同时设定门限。首先，仿真实验规定了从抽头系数开始进行迭代的前80次迭代必须先使用CMA/MCMA算法，因为均衡开始有可能因为巧合而符合了DD－LMS的切换门限，但是此时的均衡器却并没有实现到收敛到一个较小的收敛值，如果此时因巧合而启用了DD－LMS算法，则有可能造成均衡效果的发散。为了避免此种情况，增加迭代系统的稳定性，所以设定了一个常数，在迭代次数低于此常数时，不允许切换到DD－LMS算法。其次，在CMA/MCMA切换到DD－LMS算法的门限值，采用CMA误差函数定义公式(5)和剩余误差判断公式(6)，当(5)式和(6)式的误差小于常数0.6时，才切换到DD－LMS算法。以此实现两种均衡算法之间的切换。

2.剩余误差的比较分析。

在对四种均衡算法各自进行了100次每次5000个信号样本的重复试验之后，计算每次试验之后的剩余迭代误差，得出图6，可以看出四种算法都在迭代了100个信号序列之后使得剩余误差快速下降，而最终CMA算法的剩余误差非常大，MCMA与DD－LMS联合均衡算法的剩余误差非常小。其中，剩余误差的计算公式分别为:［7］

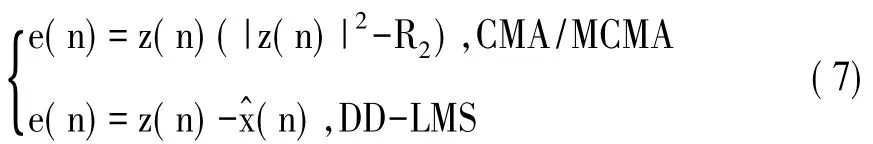
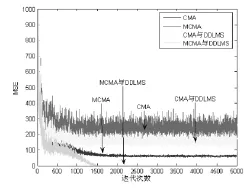
图6 均衡算法剩余误差图

四 结论

论文对各种均衡算法，以及联合均衡算法的多项性能进行了仿真验证。从中可以看出联合均衡较之CMA算法，具有更优秀的均衡效果，更小的剩余误差，可以从直观上看到联合均衡算法的星座点非常收敛，从而说明，联合均衡更有利于低信噪比，低误码率或者更恶劣的信道的传输。

［1］丁欢，王永刚.通信中的盲均衡技术［J］.现代电子技术，2007，30(11):84－87.

［2］蔡理金.CMA算法盲均衡性能分析［J］.通信技术，2011，44(12):19－20.

［3］张家琦，葛宁.联合CMA+DDLMS盲均衡算法，清华大学学报自然科学版，2009:1681－1683.

［4］Nowlan S.J.Hinton G.E，A soft decision－directed LMS algorithm for blind equalization，Communications，IEEE Transactions on Communications，1993，41(2):275－279.

［5］Fatadin I.Ives D.，Savory S.J.，Blind equalization and carrier phase recovery in a 16－QAM optical coherent system，Journal of Lightwave Technology，2009，27(15):3042－3049.

［6］李昂，段田东，方向前.基于信噪比的QAM信号盲均衡算法［J］.电视技术(S1)，2007:21－22.

［7］李世平，王爱红，王隆.基于联合误差控制的变步长双模盲均衡算法研究，微型机与应用［J］.2012，31(11): 51－54.

［8］Xu X.Chatelain B.，Plant D.V.Decision Directed Least Radius Distance Algorithm for Blind Equalization in a Dual－polarization 16－QAM System Optical Fiber Communication Conference，Optical Society of America，2012.

Blinding Equalization Algorithm for 16－QAM Signals

Zhang Jianping，Xiong Jian’guo，Zeng Xiaoling
(Chongqing Creation Vocational College，Yongchuan，Chongqing 402160，China)

This article proposed the Modify Constant Modulus Algorithm(MCMA)and Decision－Directed Least Mean Square (DD－LMS)joint equalization Algorithm to balance Inter－Symbol－Interference(ISI)at the receiving end of 16－QAM.We analyzed the joint equalization technology implementation and switching threshold.Also we had carried on simulation experiments of four different equalization algorithms.The simulation results show that MCMA and DD－LMS joint equalization algorithm can get smaller residual error iteration，also can effectively repair the transmission process of phase shift.

modify constant modulus algorithm(MCMA);decision－directed least－mean square(DD－LMS);blind equalization algorithm;joint equalization

TN919

A

1672－6758(2015)04－0046－5

(责任编辑:蔡雪岚)

张建平，硕士，讲师，重庆科创职业学院机电学院。研究方向:信息与通信系统。

Class No.:TN919 Document Mark:A