基于非线性最小二乘法的电力系统频率跟踪
高颖龙,王小华,李珍珠,卢 进
(长沙理工大学 电气与信息工程学院,湖南 长沙 410114)
基于非线性最小二乘法的电力系统频率跟踪
高颖龙,王小华,李珍珠,卢进
(长沙理工大学 电气与信息工程学院,湖南 长沙 410114)
摘要:电力系统频率是电能质量的基本指标之一,对频率的跟踪测量是电力系统正常运行、调节和控制的基础。文中提出了一种基于非线性最小二乘法实现频率跟踪的算法,并对该算法进行仿真,比较该算法和传统的基于最小二乘法的电力系统频率跟踪算法的优劣,表明该算法具有更好的精确性和实时性。
关键词:电力系统;频率跟踪;非线性最小二乘
0 引 言
频率稳定是电力系统安全稳定运行的重要因素,它反映了电力系统中有功功率供需平衡的基本状态。频率质量直接影响着电力系统的安全、稳定和优质运行,因此实现精确的频率跟踪具有重要的意义。国内外对频率跟踪的研究较多,主要有周期法,解析法,DFT类算法及其改进算法,误差最小化原理类算法等。周期法物理概念清晰易于实现,但精度不高,实时性不好;解析法计算简明,计算量不大,但是精度不高、速度也不快;DFT类算法能准确的计算出频率,考虑谐波和噪声的情况下,其各类改进算法能在一定程度上减小误差,但存在增大计算量和时滞等缺点;误差最小化算法中又包括最小二乘法,最小绝对值近似,牛顿类算法,离散卡尔曼滤波算法,这些算法在测量速度、精度、计算量、实现难易程度等方面各有优缺点。本文针对电力系统信号模型,引入一种非线性最小二乘法,通过迭代算法寻找最小误差值,从而求得电力系统频率的估计值,并对电力系统信号模型中含有奇次谐波的情形进行了详细的仿真、分析和比较。仿真结果证明了该算法的有效性、准确性。
1 基本原理
因为对于任何一个周期信号f(t)都可以用一个傅里叶级数表示,所以电力系统的模型可以表示为:
(1)
式中,an和bn是第n次谐波分量的幅值;ω0是基波角频率,ω0=2πf0,f0即为所求电力系统频率。由于在实际电力系统中可以近似认为信号不含直流分量,所以令a0=0,谐波分量最大值定义为N,于是式(1)可以写为:
(2)
可以先假定ω0是已知的,为了计算an和bn,假定f(t)是在M步长均匀采样点上,也就是说在f(tk)中k=1,2,…,M。这样就导出下面的均匀采样模型:

(3)
由电网特性可知,除基波外,3次、5次和7次等奇次谐波影响权重较大,偶次谐波与间歇波等幅值小,持续时间短,可近似忽略,因此,令n∈(1,3,5,7,…,nk),定义nk为最大谐波分量。所以可以将式(3)改写为矩阵方程:

(4)
其中:H=[HaHb]
(5)
(6)
(7)
(8)
(9)
利用最小二乘法[1]可以解得:
(10)
以上计算过程是基于ω0假定已知的前提下进行的,而实际上ω0是未知的,即H矩阵是未知的,所以该问题变成一个非线性最小二乘问题,将式(10)代入式(4)有:
(11)
从而可以得到真实值与估计值的误差e:
(12)
ω0值的确定可以通过求e的二范数的平方的最小值来确定。令
(13)
根据二范数求解方法有:
(14)
所以要求e的二范数的平方的最小值就转化为求f的最小值,当f最小时,对应的ω0即为所求。式(14)是只包含ω0一个未知参数的一元函数,所以可以用一维搜索法[2]求出f的最小值,通过一维搜索法得到的f和频率f0的关系如图1。
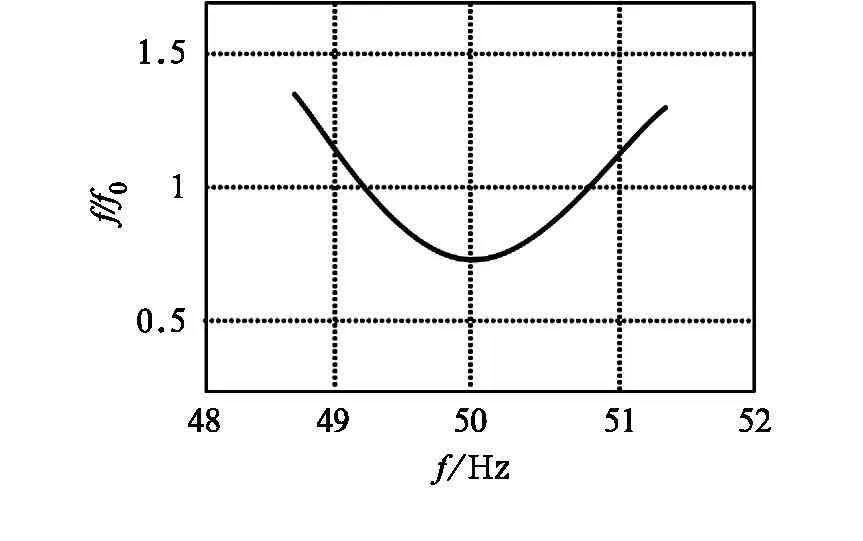
图1 根据一维搜索法得出的f和频率f0的关系图形
2 算法仿真
该算法中影响频率跟踪的因子有两个,取样间隔与谐波分量,因此在仿真的过程中针对这两个因子进行仿真。在实际电力系统中,谐波分量越高对电力系统的影响越小,所以取13次谐波分量就可以很好地对该算法进行仿真。
设定电力系统取样频率恒定为50 Hz,取样间隔为10 ms,谐波分量分别取7次谐波和13次谐波,观察在相同取样间隔的情况下谐波分量对于频率跟踪的影响,仿真结果如表1。

表1 不同谐波分量下频率跟踪误差值
由表1可知在取样间隔相同的情况下,谐波分量为7次谐波时,得到的跟踪频率值与真实值的最大误差为0.9 Hz,谐波分量为13次谐波时,得到的跟踪频率值与真实值的最大误差为0.12 Hz,通过仿真可知在取样间隔相同的情况下,谐波分量越大跟踪结果越精确。
设定电力系统取样频率恒定为50 Hz,谐波取13次分量,取样间隔分别为10 ms与20 ms进行仿真,观察在相同谐波分量的情况下取样间隔对于频率跟踪的影响,通过仿真得到表2结果。

表2 不同取样间隔下频率跟踪误差值
由表2可知在谐波分量相同的情况下,取样间隔为10 ms时,得到的跟踪频率值与真实值的最大误差为0.11 Hz;在取样间隔为20 ms时,得到的跟踪频率值与真实值的最大误差为0.02 Hz。通过仿真可知在谐波分量相同的情况下,取样间隔越大跟踪结果越精确。
最后针对电力系统模型作如下仿真,设定频率在50~54 Hz之间变化,比较基于非线性最小二乘法与基于最小二乘法[3]对该模型的跟踪结果,如图2、图3所示。图中设定频率首先在50 Hz保持不变,然后迅速变化到54 Hz再缓慢变化到50 Hz左右。
仿真结果表明,非线性最小二乘法比最小二乘法的跟踪效果好,延时更短,更准确,对于谐波的抑制能力也比较强,便于在线实时对电力系统进行跟踪。
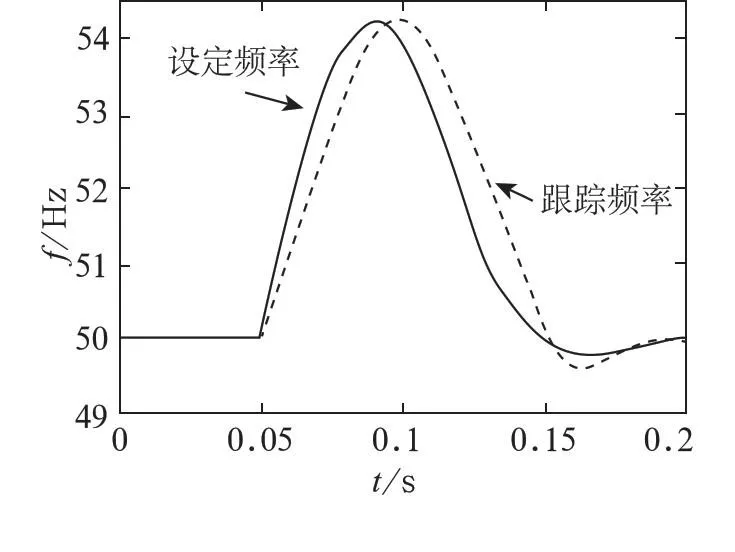
图2 基于最小二乘法的频率跟踪的仿真图形
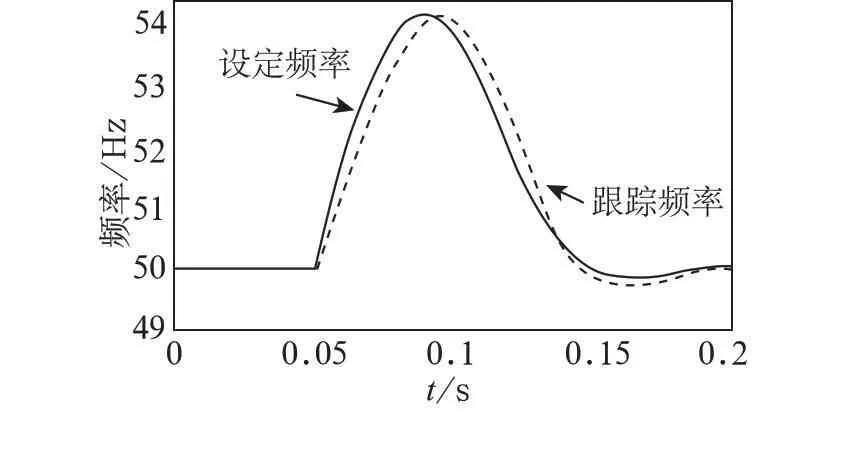
图3 基于非线性最小二乘法的频率跟踪的仿真图形
3 结 论
非线性最小二乘法通过迭代寻找最佳估计值,可以快速、准确地对电力系统频率进行跟踪,对于谐波的影响也较小,可以满足对电力系统在线实时跟踪的要求,并且精度较高、计算量较小、收敛速度比较快。
参考文献:
[1]王毅非. 最小二乘算法的研究与改进[J].继电器,2000, 28(3):5-8.
[2]张燕,徐尔. 精确一维搜索下几种共轭梯度法的分析比较[J].北京工商大学学报,2009,27(1):69-71.
[3]Miodrag D,Kusljevic,Josif J. Frequency Estimation of Three-Phase Power System Using Weighted-least-Square Algorithm and Adaptive FIR Filtering[J].2010,59(2):322-329.
研制开发
Frequency Tracking Algorithm for Power System Based on Nonlinear Least Squares Method
GAO Ying-long, WANG Xiao-hua, LI Zhen-zhu, LU Jin
(College of Electrical and Information Engineering,Changsha University of Science and Technology,Changsha 410114,China)
Abstract:Power system frequency is one of the basic indexes of power quality, and tracking and measurement of frequency is the basis of normal operation, adjustment and control of power system. The paper proposes a frequency tracking algorithm based on the nonlinear least squares method, and simulation of this algorithm was carried out. Comparisons between this algorithm and the traditional power system frequency tracking algorithm based on least square method show that the proposed algorithm has a better accuracy and real-time performance.
Key words:power system; frequency tracking; nonlinear least squares
中图分类号:TP18
文献标识码:A
文章编号:1009-3664(2015)02-0042-02
作者简介:高颖龙(1988-)男,湖南常德市临澧县人,硕士研究生,研究方向:信号处理与通信。
收稿日期:2014-12-11

