路和圈的半强积在书中的嵌入

赵斌+田应智+孟吉翔

摘要把一个图G 嵌入到书中就是把G的顶点放到书脊上，各条边嵌入到一个半平面上并且保证各条边不相交.在本文中，作者讨论了路和圈半强积的书式嵌入问题，并且给出了这些图书页数的上界.特别的，在某些条件下，作者给出了这些图确定的书页数.

关键词书式嵌入;书页数;半强积

In this paper， we only consider simple connected and undirected graphs. For a graph G， we denote all vertices by V（G） and all edges by E（G）. A book consists of a spine that is just a line and some number of pages each of which is a halfplane with the spine as boundary. A bookembedding of a graph G consists of placing the vertices of G on the line in order and assigning edges of the graph to pages so that edges assigned to same page without crossing. Page number， denoted by pn（G）， is a measure of the quality of a book embedding which is the minimum number of pages in which G can be embedded. An example in Fig.1 is helpful to understand pn（G）.

Ollmann [1] first introduced the page number problem and proved that it is NPcomplete， even if the order of nodes on the spine is fixed[23]. The book embedding problem has been motivated by several areas of computer science such as sorting with parallel stacks， singlerow routing， faulttolerant processor arrays and turning machine graphs， see [2]. Book embeddings have applications in several contexts， such as VLSI design， faulttolerant processing， sorting networks and parallel matrix multiplication[2，68].

（a） K4（b） Embedding of K4

Fig.1Embedding of K4， pn（K4）=2. The ordering of V（G） is {v1，v2，v3，v4}. In （b）， dashed line represents one page， black lines represent anotherThe semistrong product of two graphs G and H， denoted by G·H， is the graph with vertex set V（G）×V（H） and （（u1，v1）， （u2， v2））∈E（G·H） if and only if either u1u2∈E（G） and v1v2∈E（H）， or u1=u2 and v1v2∈E（H）. We denote a path and a cycle with n vertices by Pn and Cn. let V（Pn）=V（Cn）={1，2，…，n}[n].

In [4]， Bernhart gived an important theorem to fix the page number of some graphs.

Theorem 1[4]Let G be a connected graph. Then

（i） pn（G）=0 if and only if G is a path;

（ii） pn（G）≤1 if and only if G is outplanar;

（iii） pn（G）≤2 if and only if G is a subgraph of a Hamiltonian planar graph.

In next section， we will discuss the page number of semistrong product of paths.

湖南师范大学自然科学学报第38卷第6期赵斌等：路和圈的半强积在书中的嵌入1Page Number of Pm·Pn

Lemma 1If m≥3 and n>3， or m>3 and n≥3， Pm·Pn is a nonplanar graph.

ProofIf m≥3 and n>3， or m>3 and n≥3， graph Pm·Pn contains a K3，3 minor. By Theorem 10.30 in [5]， Pm·Pn is not a planar graph.

Theorem 2

pn（Pm·Pn）=1，n=2，

2，m=2， or m，n=3，

3，m≥4，n=3 or n=4.

ProofFor different m and n， we determine different pagenumber of Pm·Pn.

Case 1n=2.

Since Pm·P2 is an outplanar graph， by Theorem 1， pn（Pm·P2）=1.

Fig.2Vertex ordering and page partition of V（Pm·P3） when m is evenCase 2m=2， or m，n=3.

In this case， we consider two subcases such that pn（Pm·Pn）=2.

Case 2.1m=2.

Since P2·Pn is a subgraph of Hamiltonian planar graph， by Theorem 1， pn（P2·Pn）=2.

Case 2.1m=3 and n=3.

Graph P3·P3 is a Hamiltonian planar graph. By Theorem 1， pn（P3·P3）=2.

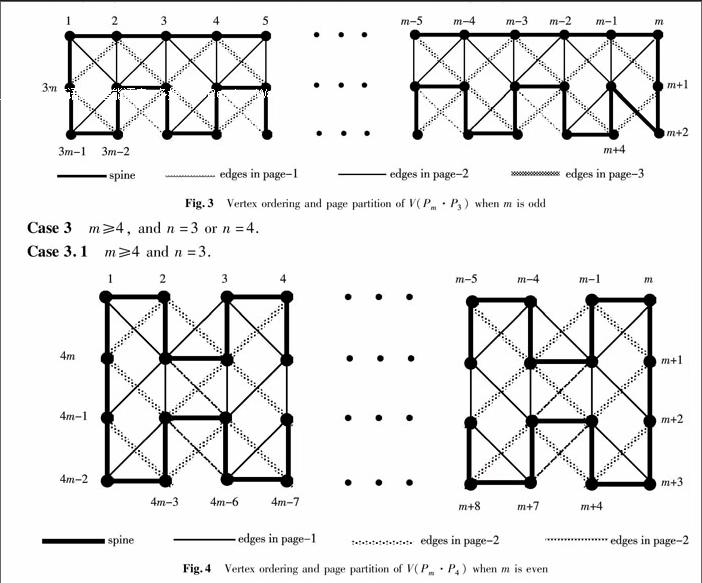
Fig.3Vertex ordering and page partition of V（Pm·P3） when m is oddCase 3m≥4， and n=3 or n=4.

Case 3.1m≥4 and n=3.

Fig.4Vertex ordering and page partition of V（Pm·P4） when m is evenBy Lemma 1 and Theorem 1， we have that pn（Pm·P3）≥3. Next， we will prove pn（Pm·P3）≤3.

When m is even， vertex ordering and page partition of V（Pm·P3） are shown in Fig.2. When m is odd， vertex ordering and edge embedding of V（Pm·P3） are shown in Fig.3.

Above all， for m≥4 and n=3， pn（Pm·P3）=3.

Case 3.2m≥4 and n=4.

By Lemma 1 and Theorem 1， we have that pn（Pm·P4）≥3. Next， we will prove pn（Pm·P4）≤3.

When m is even， vertex ordering and edge embedding of V（Pm·P4） are shown in Fig.4. When m is odd， vertex ordering and edge embedding of V（Pm·P4） are shown in Fig.5.

Above all， for m≥4 and n=4， pn（Pm·P4）=3.

Combining all the above cases， we have

pn（Pm·Pn）=1，n=2，

2，m=2， or m，n=3，

3，m≥4，n=3 or n=4.

By the definition of semistrong product， for graphs G and H， G·H has a ‘layering structure. That is to say， for a fixed vertex ui∈V（G）， let Hi be the graph with V（Hi）={（ui，vj）|vj∈V（H）} and edge set E（Hi）={（（ui，vj1）， （ui，vj2））|（vj1，vj2）∈E（H）}. We denote edge sets {（（ui，vj），（ui+1，vj+1））|i， j∈[n-1]} and {（（ui，vj），（ui-1， vj+1））|i∈[n-1]，j∈ [n]＼{1}} by E1i and E2i.

Fig.5Vertex ordering and page partition of V（Pm·P4） when m is oddTheorem 3If m≥3 and n≥5， pn（Pm·Pn）≤4.

ProofFirst， we give vertex ordering of pn（Pm·Pn）. In Pm·Pn， let Pni be a copy of Pn with i∈ [m]. So ∪mi=1V（Pni）=V（Pm·Pn）. If i is odd， we define the ordering of V（Pni） is {（1，i），（2，i），…，（n，i）}. If i is even， we define the ordering of V（Pni） is {（n，i），（n-1，i），…，（1，i）}. Denote ordering of V（Pni） by σi. Then layout vertex of Pm·Pn by the ordering： σ1，σ2，…，σm. Thus V（Pm·Pn） has an ordering already on spine， denoted by σ.

Second， we embed E（Pm·Pn） into four pages. In ordering σ， for i∈[m]， if i is odd， E1i can be embedded in one page. Edge set E2i can be embedded in another page because edges in E1i cross edges in E2i. Similarly， if i is even， E1i can be embedded in one page and E2i can also be embedded in another page. Since edges in Eji1 cross edges in Eji2， where j∈{1，2}， i1 is odd and i2 is even， and i1，i2∈[m]，（∪mi=1E1i）∪（∪mi=1E2i）  needs four pages to be embedded. Edges in ∪mi=1E（Pni） are on spine， so E（Pm·Pn） needs four pages to be embedded.

2Page Number of Cm·Pn

Theorem 4

pn（Cm·P2）=2，m is even，

3，m is odd.

ProofFor different parity of m， we give the pagenumber of Cm·P2.

When m is even， since Cm·P2 is a Hamiltonian planar graph but it is not an outplanar， by Theorem 1， pn（Cm·P2）=2.

When m is odd， if m=3， Cm·P2 is K3，3. By Theorem 10.30 in [5]， Cm·P2 is not a planar graph for m≥3. Therefore， by Theorem 1， pn（Cm·P2）≥3.

Next， we give upper bounds of pn（Cm·P2）. We denote edges （（m，1）， （1，2）） and （（m，2），（1，1）） by e1 and e2. So E（Cm·P2）=E（Pm·P2）∪e1∪e2. By Theorem 2， pn（Pm·P2）=1. Since e1 crosses with e2 and edges in E（Pm·P2）， e1 needs one page to be embedded. Similarly， e2 needs another page to be embedded. So pn（Cm·P2）≤3. Above all， pn（Cm·P2）=3.

Combining all the above conditions， the theorem has been proved.

Theorem 5If m is even and n≥3， pn（Cm·Pn）≤4.

ProofDenote edge sets {（（m，i），（1， i+1））|i=1，2，…，n-1} and {（（m，i），（1，i-1））|i=2，3，…，n} by E1 and E2. So E（Cm·Pn）=E（Pm·Pn）∪E1∪E2. Denote vertex ordering of Pm·Pn in Theorem 2.3 by σ. Since V（Cm·Pn）=V（Pm·Pn）， layout V（Cm·Pn） on spine by σ. In this ordering， E（Pm·Pn） needs four pages to be embedded. Edge sets E1 and E1i， when i is even， can be embedded in a same page. Similarly， E2 and E2i， where i is even， can be embedded in a same page. Therefore， pn（Cm·Pn）≤4.

3Page Number of Pm·Cn and Cm·Cn

Theorem 6

pn（Pm·Cn）≤4m=2 and n≥3，

≤6m，n≥3.

ProofWe denote {（（i，n）（i+1，1））|i=1，2，…，m-1}， {（（i，1）（i+1，n））|i=1，2，…，m-1} and {（（i，1）（i，n））|i=1，2，…，n} by E1c， E2c and Ec. By the definition of semistrong product， we know that V（Pm·Cn）=V（Pm·Pn） and E（Pm·Cn）=E（Pm·Pn）∪E1c∪E2c∪Ec. Layout V（Pm·Cn） on spine by the ordering of V（Pm·Pn） in Theorem 3. In the ordering， E（Pm·Pn） needs four pages to be embedded. Edge sets E1c and Ec can be embedded in one page. Edge set E2c needs another one. Since edges in E1c and Ec cross edges in E2c and E（Pm·Pn）， the pagenumber of Pm·Cn is at most six. Specially， If m=2， E（Pm·Pn） only needs two pages to be embedded. So， pn（Pm·Cn）≤4 for m=2.

Theorem 7If m，n≥3 and m is even， pn（Cm·Cn）≤6.

ProofBy the definition of semistrong product， we know that V（Cm·Cn）=V（Cm·Pn） and E（Cm·Cn）=E（Cm·Pn）∪E1c∪E2c∪Ec. Layout V（Cm·Cn） on spine by ordering of V（Pm·Pn） in Theorem 3. Hence E1c and Ec can be embedded in one page， and E2c needs another one. Due to edges in E1c and Ec cross edges in E2c and E（Cm·Pn）， by Theorem 5， pn（Cm·Cn）≤6.

4Conclusion

In this work， we give the upper bounds of Pm·Pn， Cm·Pn， Pm·Cn and Cm·Cn. For different n and m， we have different results. Under some conditions， we can determine the exact page number of these graphs. But semistrong product of two arbitrary graphs G and H is very complex， we leave it for future study.

References：

[1]OLLMANN L T. On the book thicknesses of various graphs [C]//Proc. 4th southeastern conference on combinatorics， Graph theory and computing， Congressus Numerantium， Winnipeg： Utilitas Mathematics Publ. Inc.， 1973. VIII 459.

[2]CHUNG F R K，  LEIGHTON F T， ROSENBERG A L. Embedding graph in books： a layout problem with applications to VLSI design [J]. SIAM J Alg Disc Math， 1987，8（1）：3358.

[3]SHAHROKHI F， SHI W. On crossing sets， disjiont sets and pagenumber [J]. J Algor， 2000，34（1）：4053.

[4]BEMHART F， KAINEN B. The book thickness of a graph [J]. J Comb Theory B， 1979，27（3）：320331.

[5]BONDY J A， MURTY U S R. Graph theory with application [M]. Berlin：Springer， 2008.

[6]HEATH L S， LEIGHTON F T， ROSENBERG A L. Compariting queues and stacks as mechanisms for laying out graphs [J]. SIAM J Discrete Math， 1992，5（3）：398412.

[7]ROSENBERG A L. The diogenes approach to testable faulttolerant arrays of processors[J]. IEEE Trans Comput， 1983，32（10）：902910.

[8]TARJAN R E. Sorting using networks of queues and stacks [J]. J Appl Comput Math， 1972，19（2）：341346.

[9]KAPPOOR N， RUSSELL M， STOJMENOVIC I， et al. A genetic algorithm for finding the pagenumber of interconnection networks [J]. J Parallel Distr Com， 2002，62（2）：267283.

[10]YANNAKAKIS M. Embedding planar graph in four pages [J]. J Comput Syst Sci， 1989，38（1）：3637.

[11]BILSKI T. Optimum embedding of complete graphs in books [J]. Discrete Math， 1998，182（13）：2128.

[12]FANG J F， LAI K C. Embedding the incomplete hypercube in books [J]. Inform Process Lett， 2005，96（1）：16.

[13]SPERFELD K. On the page number of complete oddpartite graphs [J]. Discrete Math， 2013，313（17）：16891696.

[14]岳为君， 黄元秋， 赵霆雷，等. 一个特殊5阶图与圈e的联图的交叉数[J]. 湖南师范大学自然科学学报， 2015，38（1）：8185.