Scaled Boundary Finite Element Method for Thermoelasticity in Voided Materials

Jan Sladek,Vladimir Sladekand Peter Stanak

Scaled Boundary Finite Element Method for Thermoelasticity in Voided Materials

Jan Sladek1,Vladimir Sladek1and Peter Stanak1

The scaled boundary finite element method （SBFEM）is presented to study thermoelastic problems in materials with voids.The SBFEM combines the main advantages of the finite element method （FEM）and the boundary element method （BEM）.In this method,only the boundary is discretized with elements leading to a reduction of spatial dimension by one.It reduces computational efforts in mesh generation and CPU.In contrast to the BEM,no fundamental solution is required,which permits to analyze general boundary value problems,where the conventional BEM cannot be applied due to missing fundamental solution.The computational homogenization technique is applied for thermo-mechanical analyses in voided materials.The evolution of the mechanical and thermal fields at the macroscopic level is resolved through the incorporation of the microstructural response.The microstructural analyses are performed on the representative volume element（RVE）,where essential physical geometrical information about the microstructural components is included.

Representative volume element（RVE）,circular voids,2-d problems,uncoupled thermoelasticity.

1 Introduction

The presence of voids affects material properties and functionality of these elements in structures.It is needed to have reliable computational models to consider voids in materials.For voided isotropic or anisotropic materials,the influences of voids on the effective properties have been studied by many authors[Christensen（1993）;Jasiuk et al. （1994）].The shape and distribution of voids can be arbitrary.In principle it would be possible to refer directly to the microscopic scale,but such microscopic models are often far too complex to handle for the analysis of a large structure.Further,the data obtained would be redundant and compli-cated procedures would be required to extract information of interest.Therefore,the multiscale modelling is a convenient technique to consider microstructure properties and transfer them into the macroscopic models The scope of such multiscale modelling is to design combined macroscopic-microscopic computational methods that are more ef ficient than solving the full microscopic model and at the same time give the information that we need to the desired accuracy[Engquist et al. （2007）]The microstructure can be accounted in macro-structural analyses via homogenization when the effective （overall）material coef ficients are obtained from solutions of appropriate boundary value problems on micro-scale level in a representative volume element（RVE）[Hill（1963）].

In literature there are many homogenization techniques and earlier methods have been based on analytical approaches.Mainly self-consistent and Mori-Tanaka analytical approaches are utilized to get effective material coef ficients[Budiansky（1965）;Hill（1965）;Mori and Tanaka （1973）;Benviste （1987）;Kachanov （1992）;Castaneda and Willis （1995）;Quin （2004）;Goyheneche and Cosculluela （2005）].AcomprehensivevalidationofanalyticalhomogenizationmodelsisgivenbyGhossein and Levesque （2014）.Later,numerical approaches have been developed to determine effective material properties in composite materials[Bohm and Han（2001）;Bohmetal.（2002）;Marur（2004）;Pierardetal.（2004）].Higher-ordertwodimensional as well as low and higher-order three-dimensional new hybrid-mixed finiteelementsbasedonindependentlyassumeddisplacement,andjudiciouslychosen strain fields are developed in[Bishay and Atluri（2012）;Dong and Atluri（2011,2012）]for applications in macro-and micro-mechanics.These schemes can be also applied forproblems such as the determination ofthe effectivethermal conductivity of porous rocks in partially saturated conditions[Gruescu et al. （2007）].Various multiscale methods are reviewed by Kanoute et al. （2009）in the context of modelling mechanical and thermomechanical responses of composites.In the present paper a pure numerical approach has been developed to evaluate thermomechanical effective material properties in a voided material.Numerical analyses are performed on the RVE.The RVE contains sufficient microstructural information to be representative of any similar volume taken from any location in the voided solid.In uncoupled thermoelasticity,the temperature field is not influenced by displacements.Therefore,the heat conduction equation is solved first to obtain the temperature distribution.The equation of motion is subsequently solved for mechanical quantities.

The number of literature sources on the complex thermomechanical problem is limited.However,there are some literature sources on evaluation of effective thermal conductivity coefficients[Progelhof et al. （1976）;Han and Cosner （1981）;Hatta and Taya （1986）;Gordon et al.（1994）;Milton （2000）;Sevostianov and Kachanov（2003）;Ahmedi et al.（2010）;El Moumen et al.（2015）;Wu et al.（2013）].In homogenization techniques the RVE under specific boundary conditions is analyzed for determination of influence of voids on material properties.Therefore,we need to have a reliable computational tool to solve boundary value problems on the RVE.The finite element method （FEM）,boundary element method （BEM）and meshless methods have been successfully applied to boundary value problems in thermoelasticity[Druma et al. （2004）;Sladek and Sladek （1984）;Suh and Tosaka （1989）;Dargush and Banerjee （1991）,Shiah and Tan （1999）;Kögl and Gaul（2003）].A novel approach to identify the thermal conductivities of a thin anisotropic medium by the BEM is presented by Shiah et al. （2014）.Four representative multiscale methods,namely asymptotic homogenization method （AHM）,heterogeneous multiscale method （HMM）,variational multiscale （VMS）method and multiscale finite element method （MsFEM）,for elliptic problems with multiscale coefficients are surveyed by Wu et al.（2014）.

The scaled boundary finite element method （SBFEM）is developed in the present paper for 2D boundary value problem in a porous elastic solid under stationary thermoelastic boundary conditions.Up to now the SBFEM have been successfully applied to elastostatic,elastodynamic problems,thermopiezoelectricity and piezoelectric crack problem too[Deeks and Wolf（2002a）;Song （2004a）;Chiong et al.（2014）;Li et al. （2014,2015）].The domain is described by scaling the boundary with the dimensionless radial coordinate pointing from the scaling center.Only the boundary of the domain is discretized with line elements.A scaling center is selected at a point from which the whole boundary is directly visible.However,the analyzed domain is frequently discretized by more polygons than it is necessary to satisfy the visibility condition to reduce the number of unknowns in the polygon.Song （2004b）has developed a super element for the dynamic analysis of two-dimensional crack problems.Although a quadratic eigenvalue problem must be solved in the scaled boundary finite-element method,the cost of which increases rapidly as the number of degrees of freedom increases,the scaled boundary finite-element method out-performs the finite-element method in situations involving stress concentrations or unbounded domains,reducing signi ficantly the program run-time and using only a fraction of the number of degrees of freedom.The h-hierarchical adaptive procedure for the scaled boundary finite-element method has been developed by Deeks and Wolf（2002b）.

The SBFEM has been developed here for uncoupled thermoelasticity and it is applied for evaluation of effective material properties on the micro-level（RVE）of the elastic solids with voids.Special boundary conditions are considered to evaluate individual material parameters.The present analyses give information concerning how the homogenized thermoelastic properties of the material vary in terms of porosity.

2 Governing equations in thermoelasticity

Consideralinearelasticsolidunderstationaryconditionssinceweareinterestingto investigate influence of microstructure on macro model behavior.Governing equations are given by the balance of forces and stationary heat conduction equations[Nowacki（1986）]

where σij, θ and uiare the stresses,temperature difference and displacements,respectively.Symbol kijis used for the thermal conductivity tensor.Constitutive equations are given by the well known Duhamel-Neumann constitutive law for the stress tensor

where cijklare the materials elastic coefficients and γijis the stress-temperature modulus.The stress-temperature modulus can be expressed through the elastic coefficients and the coefficients of linear thermal expansion αklas

For 2-D plane problems,the constitutive equation （3）is frequently written in terms of the second-order tensor of elastic constants[Lekhnitskii（1963）].Making use the standard Voigt notation,the constitutive equation for orthotropic materials and plane strain problems has the following form

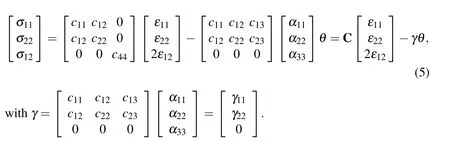
In the present paper only orthotropic material properties are considered.However,the SBFEM can be applied also for a general anisotropic material.If material properties are isotropic,equation （5）is reduced to a simple form with Lame’s constants λ and µ .

The following essential and natural boundary conditions are assumed for the mechanical quantities

and for the thermal quantities

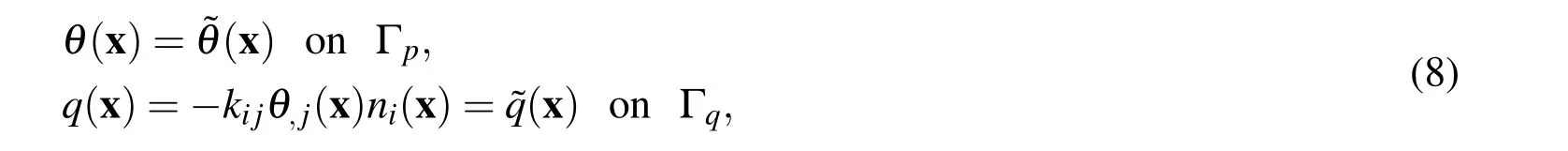
where q（x）is heat flux,Γuis the part of the global boundary with prescribed displacements,while on Γt,Γpand Γqthe traction vector ti,the temperature and the heat flux are prescribed,respectively.

Since mechanical and thermal quantities are uncoupled,in the first step the temperature solution can be computed and in the next problem the mechanical quantities are analyzed.

3 Scaled boundary finite element method for stationary heat conduction problem

Recently,the scaled boundary finite element method （SBFEM）has been developed for stationary heat conduction problem[Li et al.（2015）].A scaling center O is selected at a point from which the whole boundary is directly visible.The boundary S is scaled by the dimensionless radial coordinate ξ pointing from the scaling center.Figure 1 illustrates the basic idea of the scaled boundary finite element method for a 2D problem with domainV.Only the boundary S of the domain is discretized with line elements Sewhen applying the scaled boundary finite element method.Then,the whole analyzed domain V is decomposed into triangular sectors Veassociated with the boundary line elements Se.

The global Cartesian coordinates （x,y）of a point of a line element Se（the superscript e denotes the element）on the boundary are parametrized as

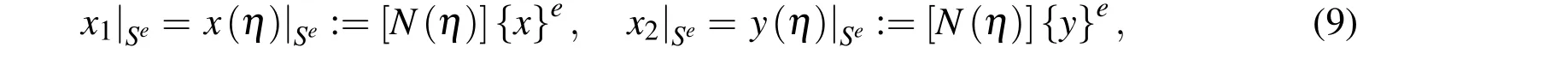
with η being the local （circumferential）coordinate η ∈ [-1,1],[N （η）]=（N1（η）,N2（η））is the 1×2 matrix of shape functions N1（η）= （1- η）/2,N2（η）= （1+η）/2,and{x}e,{y}eare 2×1 vectors composed of the Cartesian coordinates of two nodal points on the boundary element Se,i.e.

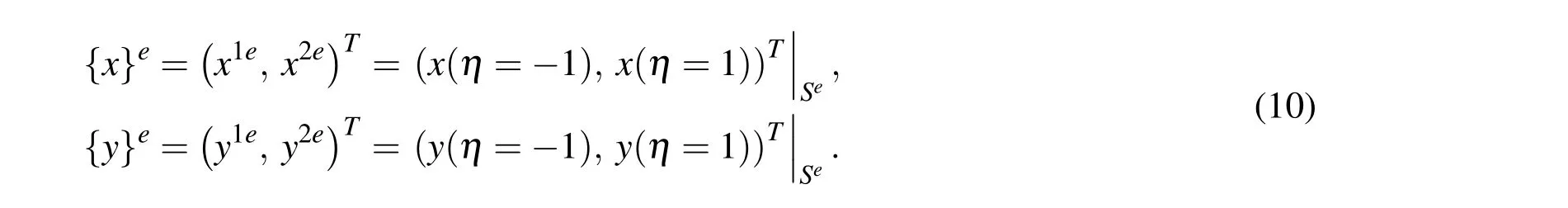
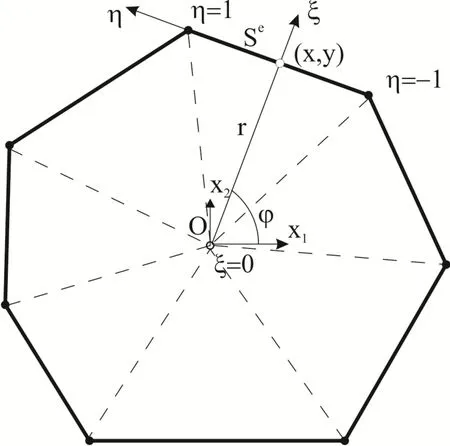
Figure 1:The scaled boundary polygon representation.

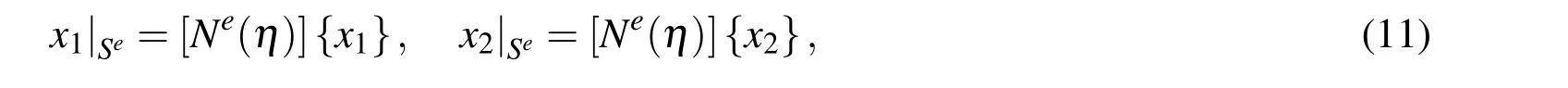
where the shape functions matrix[Ne（η）]is 1×n matrix with the a-th element of this matrix being given as

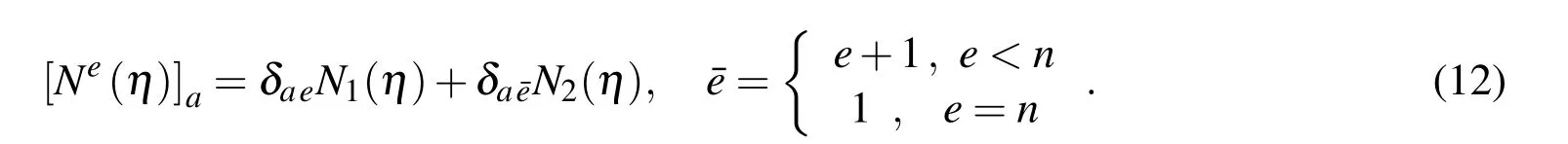
The analyzed domain is described by scaling the boundary with the dimensionless radial coordinate ξ pointing from the scaling center O（ξ =0）to a point on the boundary （ξ =1）.TheCartesiancoordinates（x1,x2）ofa point inside thetriangular sectorVeare parametrized as

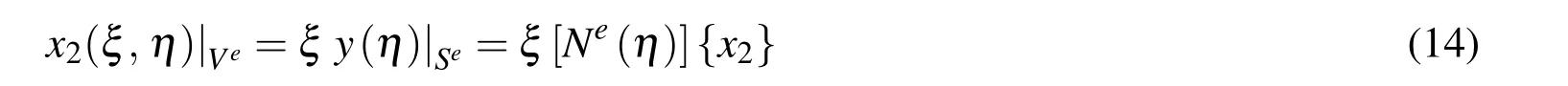
where ξ and η are called the scaled boundary coordinates,ξ ∈ [0,1],η ∈ [-1,1].Thescaledboundarycoordinatesintwodimensionsresemblethepolarcoordinates.The polar coordinates shown in Figure 1 are expressed as

Now,we extend the assumed interpolation on the boundary element,i.e.the approximation of the dependence on the parameter η when ξ=1,also to interior points in the sectorVeas

The transformation between the components of the gradient operator in the Cartesian coordinate system and scaled boundary coordinate system is shown as

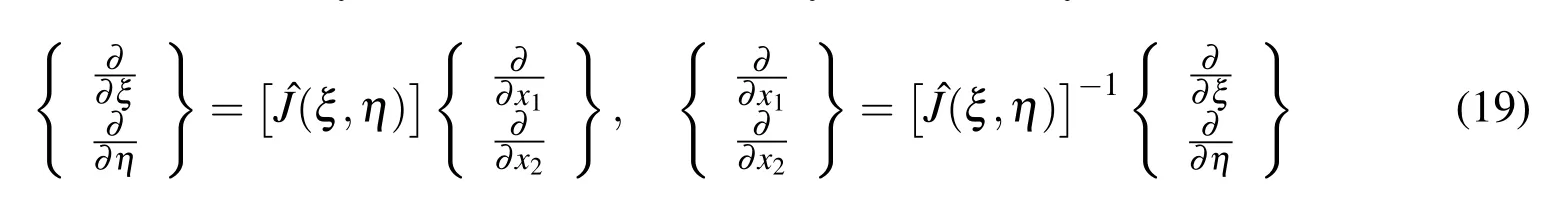
with the Jacobian matrix defined as

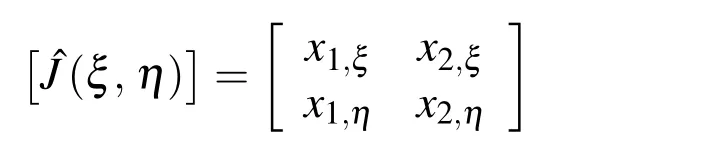
with the radial coordinate ξ being separated from the local coordinate η on the boundary.The matrix[J（η）]is the Jacobian matrix on the boundary （ξ =1）,i.e.

and its determinant is

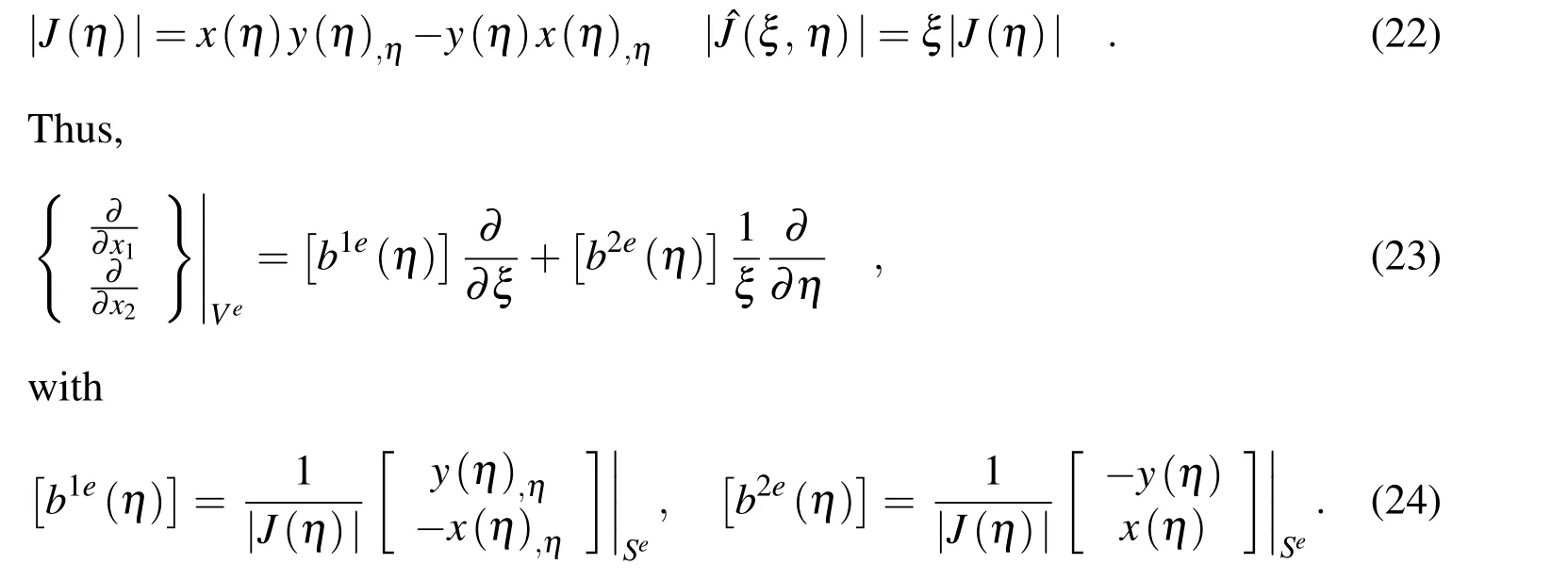
Then,the heat flux vector defined by

can be approximated on the sector Veas

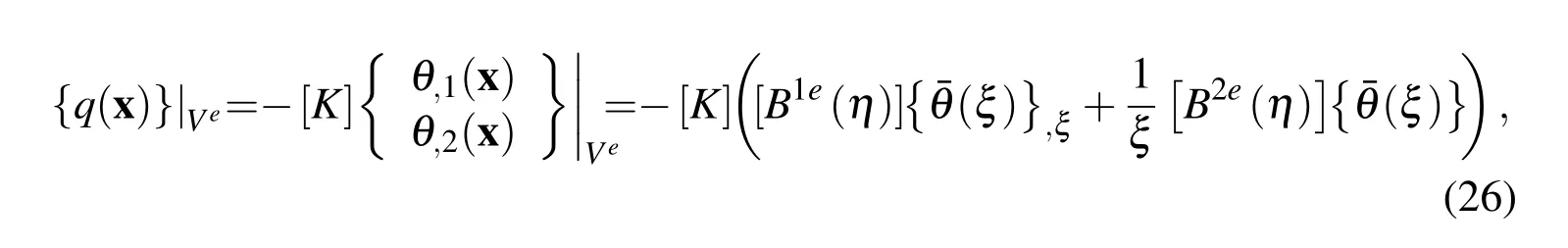
where{q（x）}= （q1（x）,q2（x））T,and

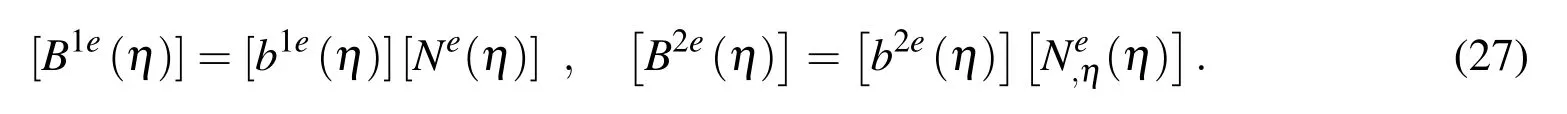
The governing equation （2）and the prescribed boundary conditions result from the variational formulation

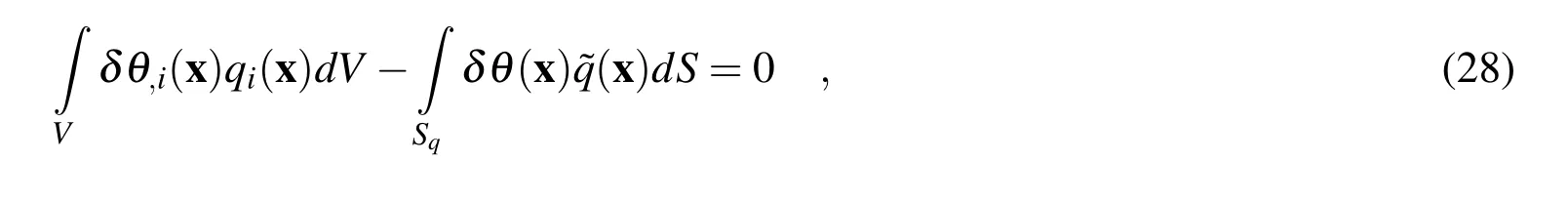
or equivalently

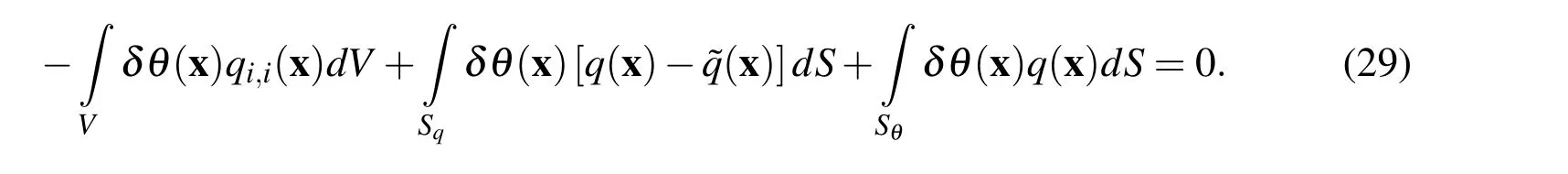
Bearing in mind the approximations over the sectors Veand/or the boundary elements Se

with using the transformation of the integration variables,one can rewrite Eq.（28）as

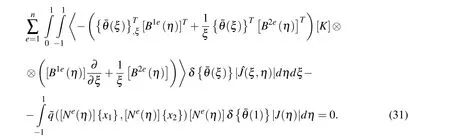
Introducing the notations

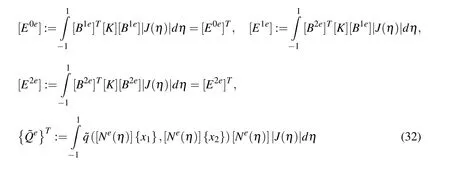
and taking into account|ˆ J（ξ,η）|= ξ|J（η）|,we rearrange Eq.（31）as

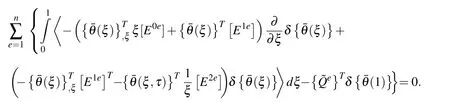
Hence,integrating the first term by-parts,we receive

where we have used the notation

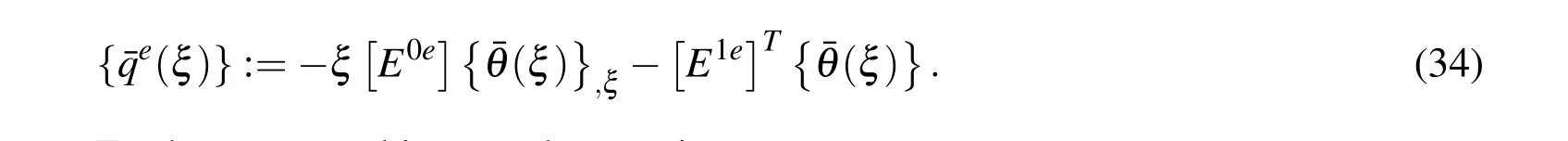
Furthermore,making use the notations

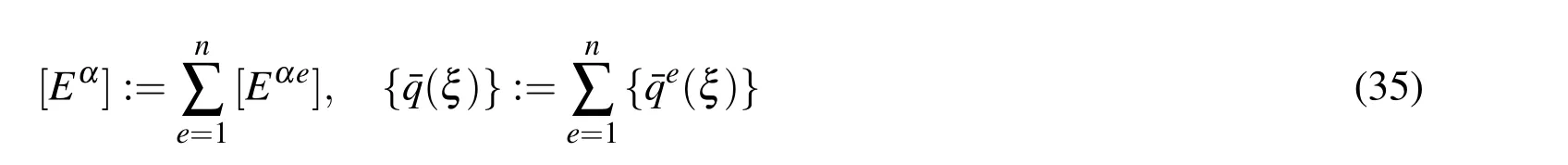
the variational formulation yields the following governing equation

and the restriction conditions on the boundary

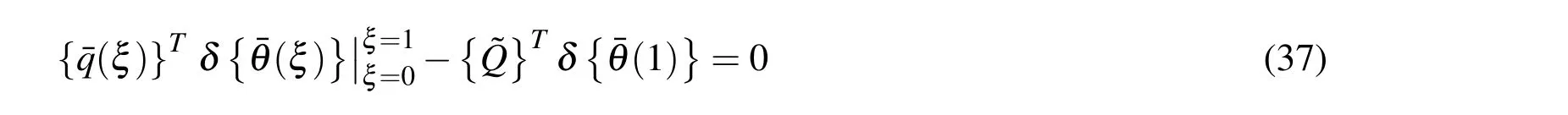
which can be rearranged as

Now,the restriction condition （38）yields two kinds of boundary conditions:

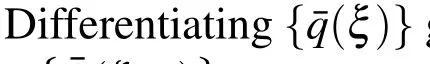
with the Hamiltonian coefficient matrix

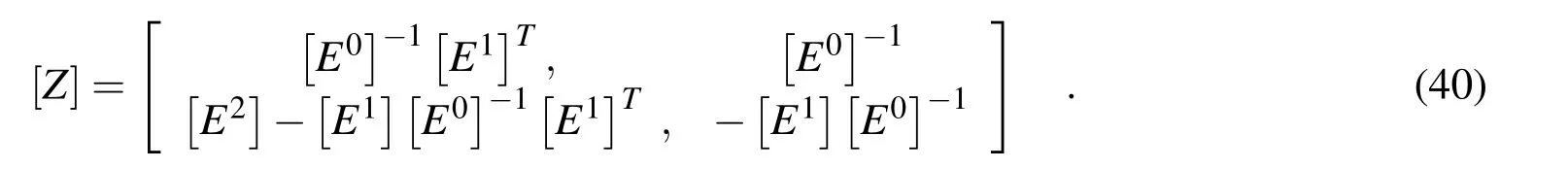
The eigenvalue method[Song and Wolf（1999）]has been applied to solve the system of ordinary differential equations（ODE）.The general solution of equation （39）is given by

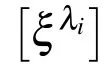
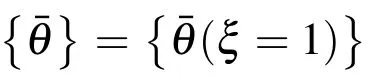
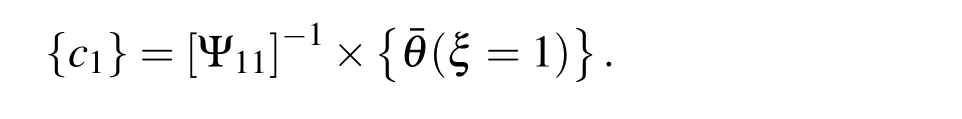
The nodal fluxes on the boundary are obtained from equation （44）

If the stiffness matrix[K]is defined as

4 Scaled boundary finite element method for stationary elasticity

The strain{¯ε}is given as

with the linear differential operator

The operator[L]can be utilized to rewrite equilibrium equations（1）as

Again the whole analyzed domain V is decomposed into triangular sectors Veassociated with the boundary line elements Seand the Cartesian coordinates（x,y）on the boundary Seare interpolated by nodal coordinates and shape functions.The scaled coordinates ξ and η are introduced.

Thelineardifferentialoperator[L]inequation（48）istransformedtothecoordinates ξ,η as

Substituting equations（50）and （53）into equation （37）leads to

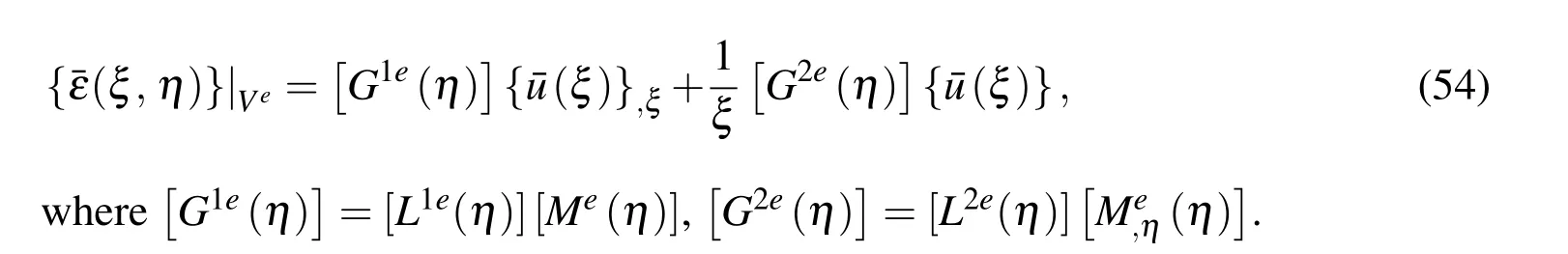
The stresses{¯σ（ξ,η）}can be obtained at any point（ξ,η）inside the sector Vefrom equations（5）and （54）as

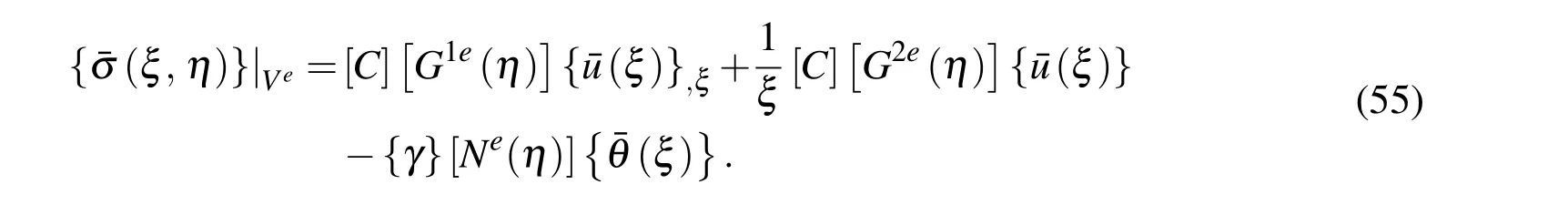
Now,we can formulate the principle of virtual work for considered problem as

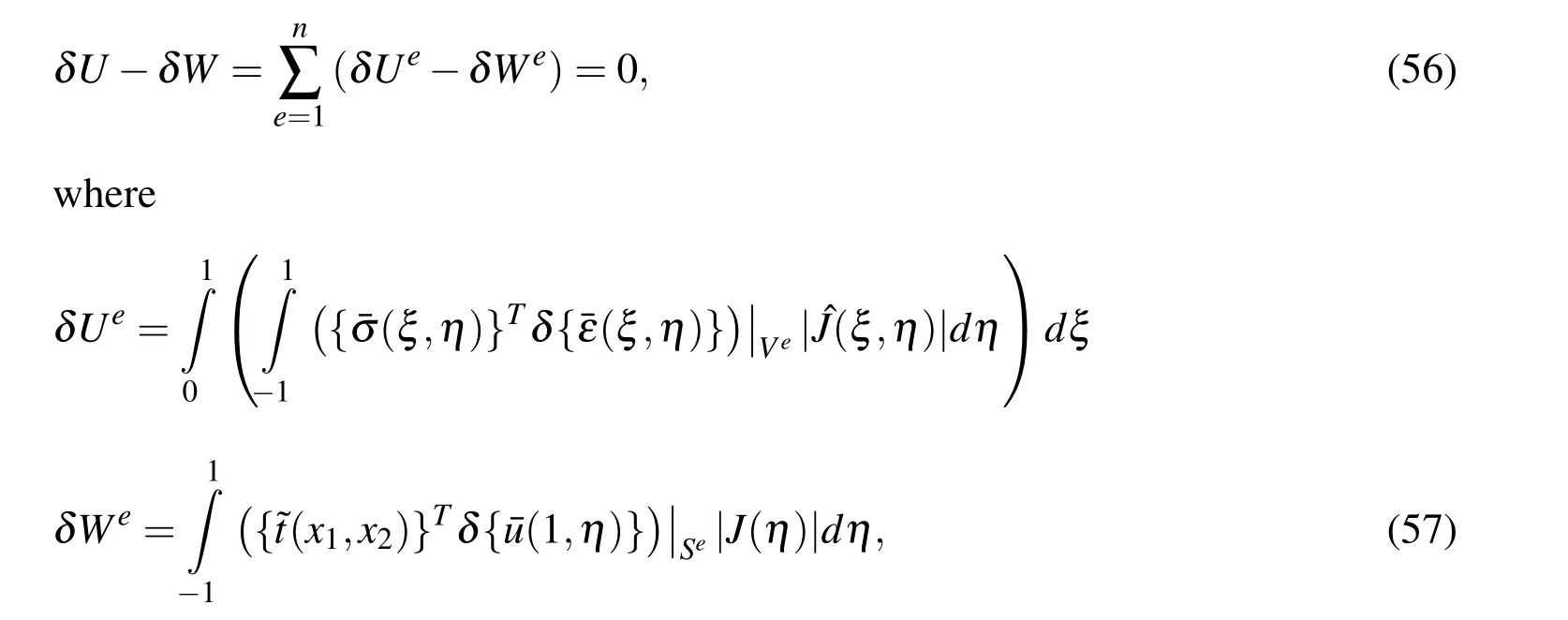
In view of（55）and （53）,one obtains

According to （56）-（59）,the principle of virtual work results into the governing equation

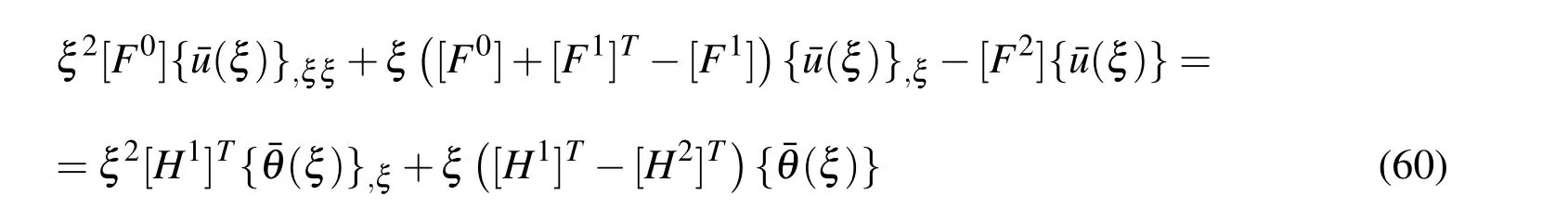
and the restriction condition

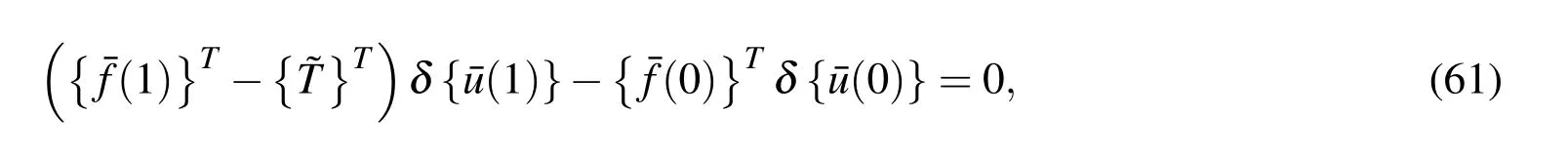
which can be rearranged as

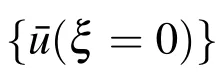
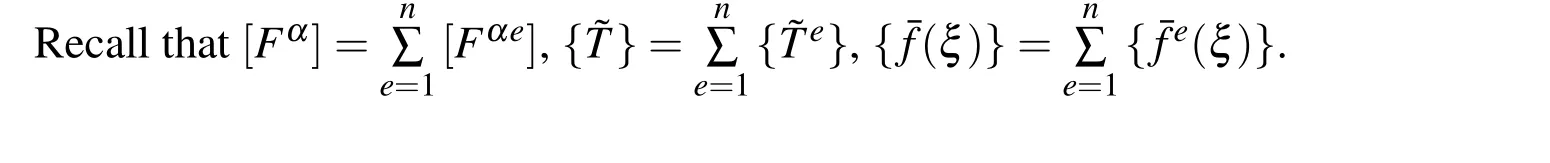
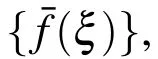
where the right-hand side vector and the Hamiltonian coefficient matrix are given by

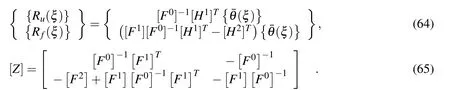
The eigenvalue method[Song （2004a）]has been applied to solve the homogeneous equationcorrespondingtothescaledboundary finiteelementmethodequation （63）,firstly.Substituting the formal solution

into homogeneous system leads to the eigenvalue problem of matrix[Z]

where[λ]is diagonal matrix composed of 4n eigenvalues and the columns of the matrix[Ψ]are given by the corresponding eigenvectors.

Separating the positive and negative eigenvalues,one can split the general solution of the homogeneous system as

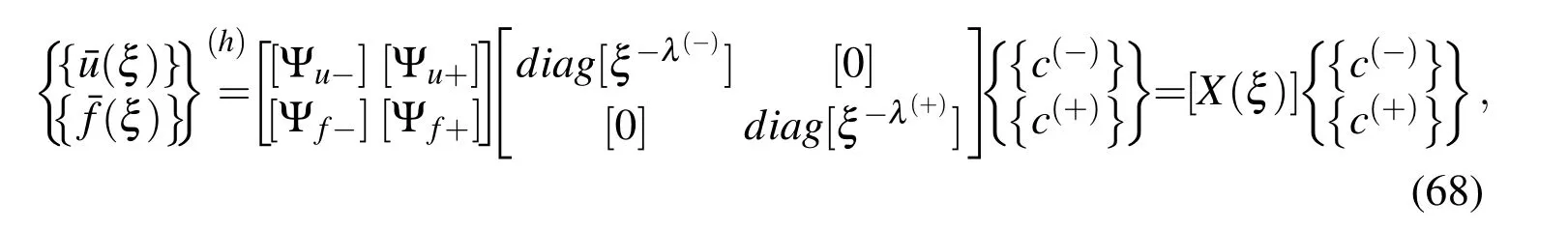
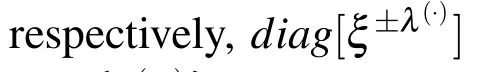
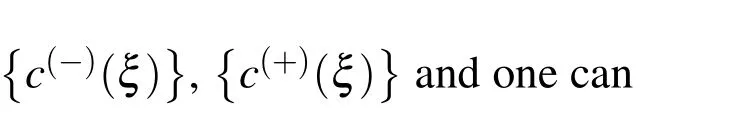
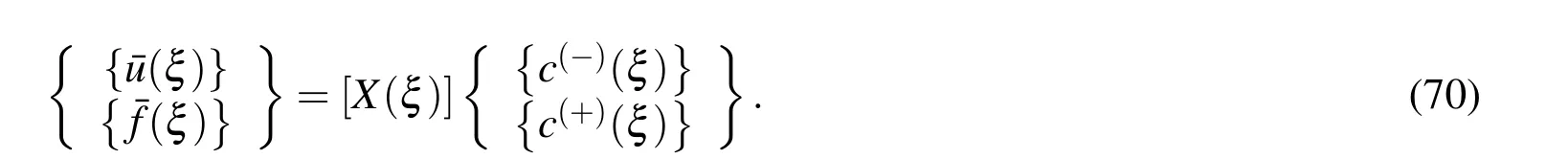
Substituting （70）into （63）yields

Hence,in view of（69）

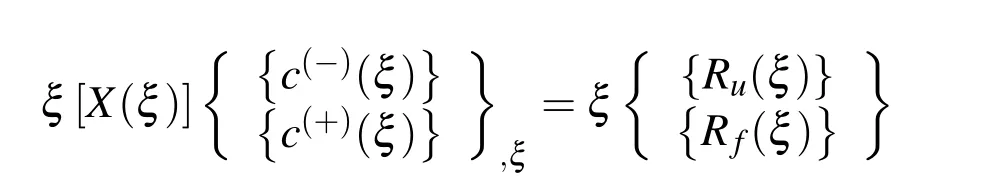
or according to （68）

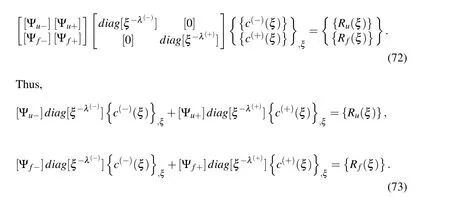
Hence,we obtain

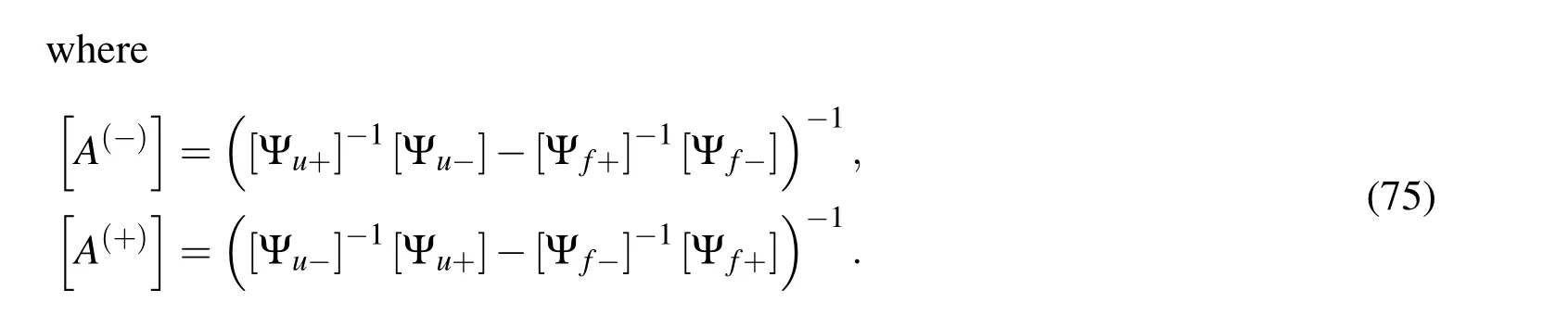
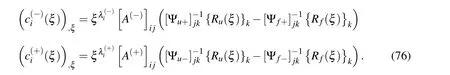
Integrating equations in （76）,we obtain

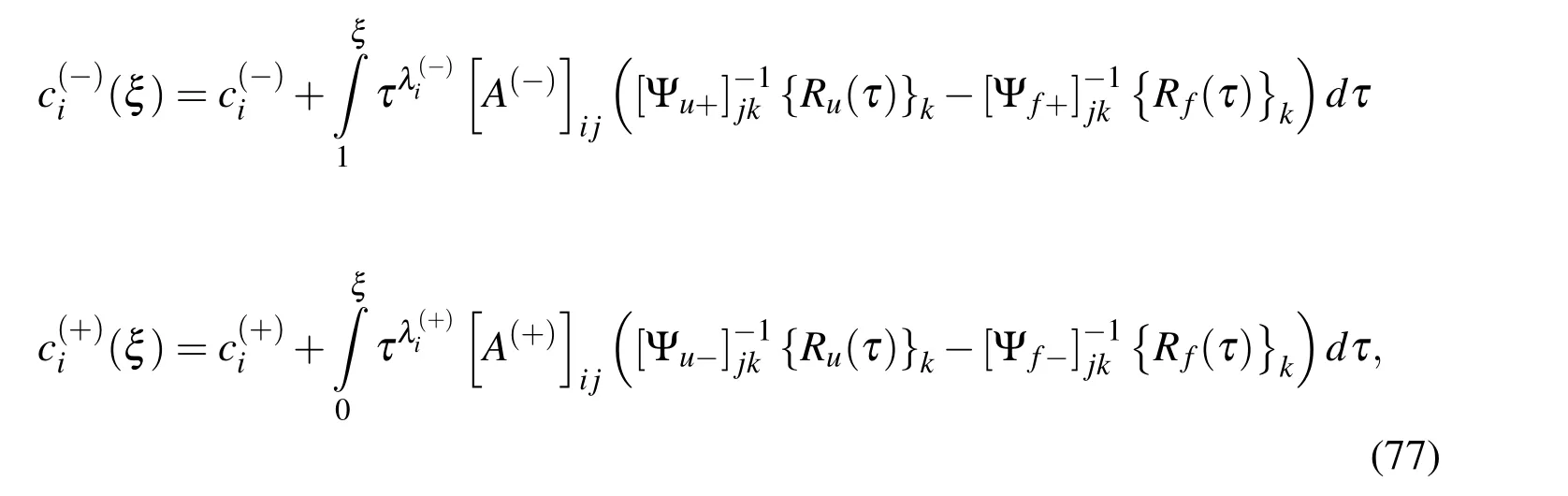
Eq.（79）represents two sets of 2n relationships

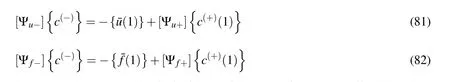
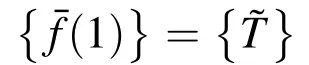
5 Computation of effective thermal and elastic material properties

Let us consider a rectangular RVE sample Ω ={∀x= （x1,x2）;x1∈ [0,a],x2∈[0,b]}.Inside the rectangular RVE domain there are generally some microstructural elements with arbitrary geometry.Then,the average values of the conjugated fields within the analysed sample are given as

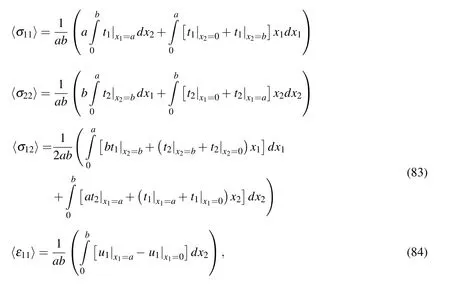
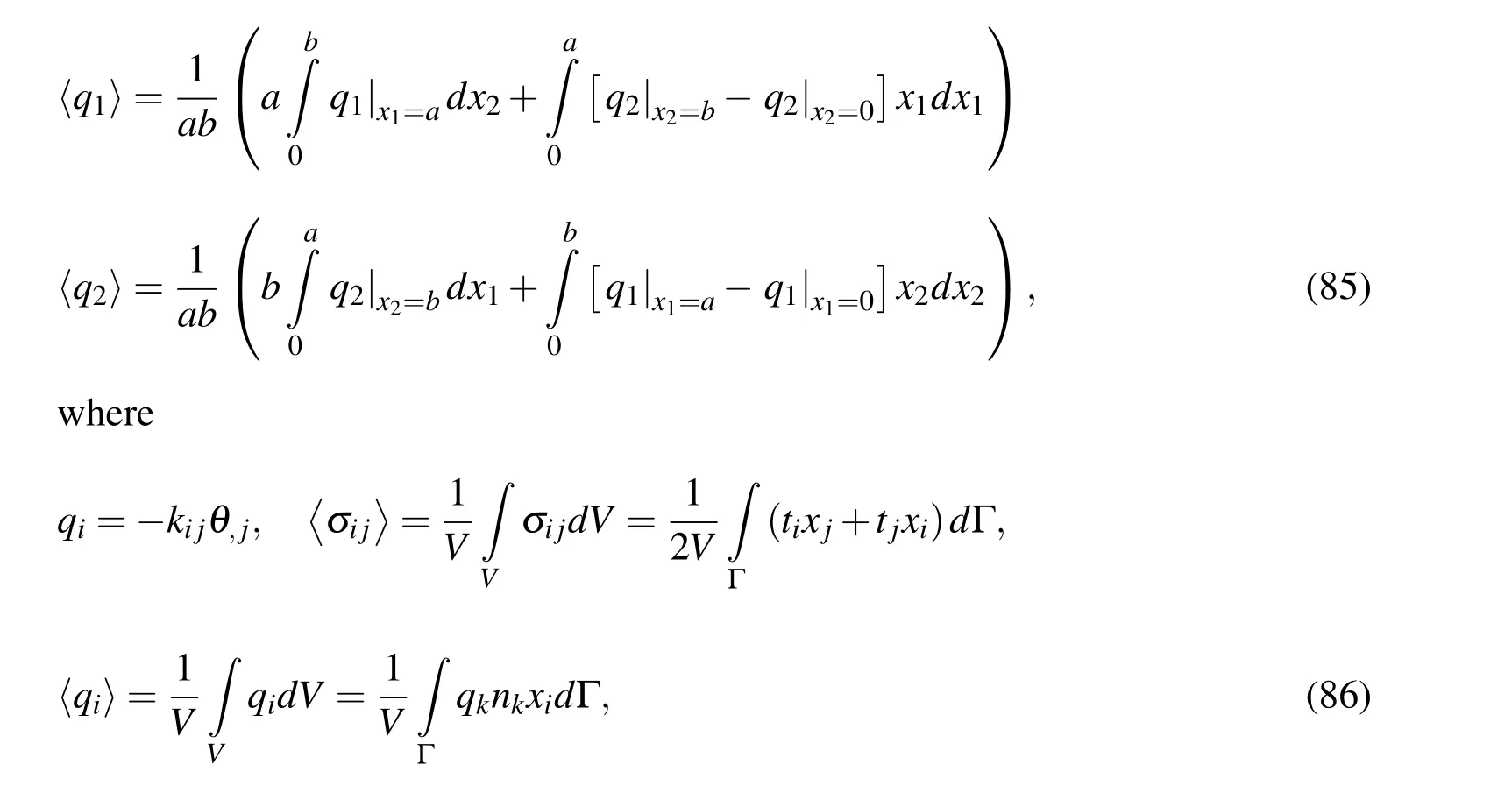
and the integrands are obtained from the solution of considered boundary value problems.

If the boundary conditions are selected as shown in Fig.2,the average values of the secondary fields are given as

Then,we can get the following effective material coefficients

If the boundary conditions are selected as shown in Fig.3,the average values of the secondary fields are given as

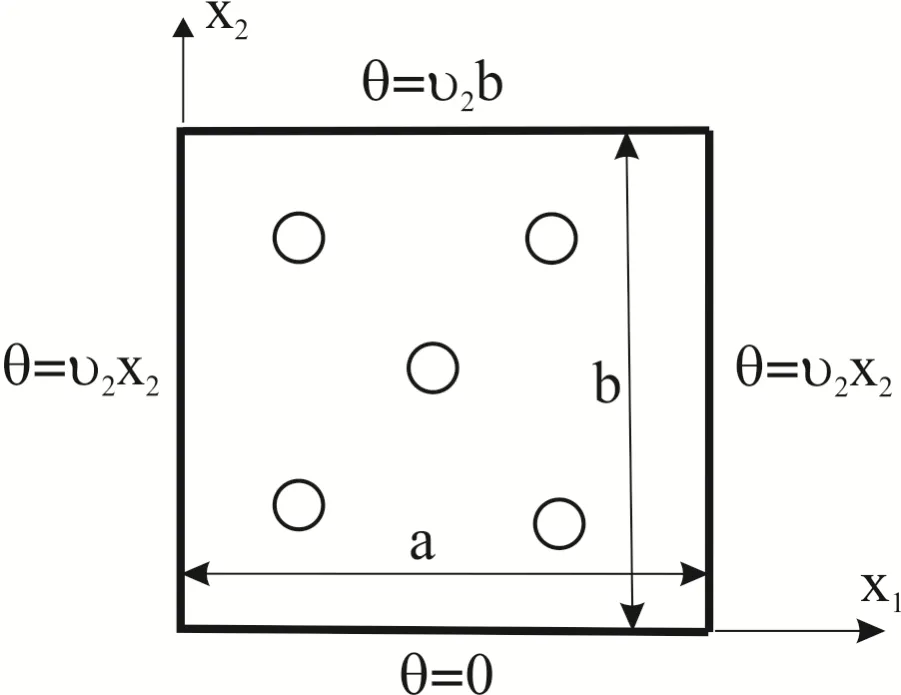
Figure 3:Boundary conditions appropriate for evaluation of

Now,we can calculate the following effective material coefficients

where the average values of the conjugated fields 〈q1〉,〈q2〉are given by formulae （85）,with the integrands being obtained from the solution of the considered boundary value problem.

Now,the effective mechanical material parameters can be computed.If boundary conditions are selected as shown in Fig.4,the average values of the secondary fields are given as

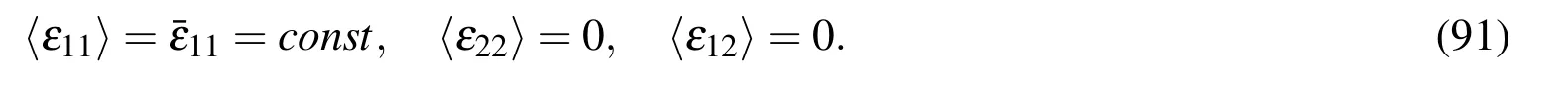
Figure 4:Boundary conditions appropriate for evaluation of

Then,we can get the following effective material coefficients

If the boundary conditions are selected as shown in Fig.5,the average values of the secondary fields are given as

Now,we can calculate the following effective material coefficients

where the average values of the conjugated fields 〈σ11〉,〈σ22〉are given by formulae （83）,with the integrands being obtained from the solution of the considered boundary value problem.

If effective elastic coefficients are available,we can calculate the stress-temperature effective material coefficients.For selected boundary conditions in Fig.6,the average values of the secondary fields are given as

Figure 5:Boundary conditions appropriate for evaluation of

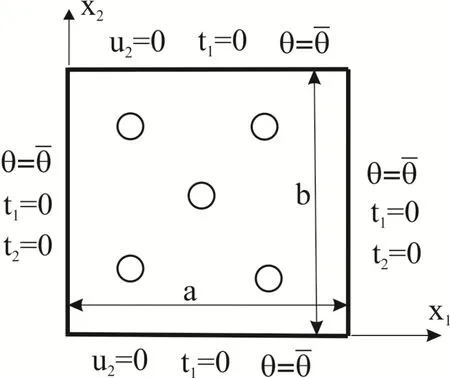
Figure 6:Boundary conditions appropriate for evaluation of

The stress-temperature effective material coefficients are derived from vanishing〈σ11〉and constitutive equation for〈σ22〉.They have the following form

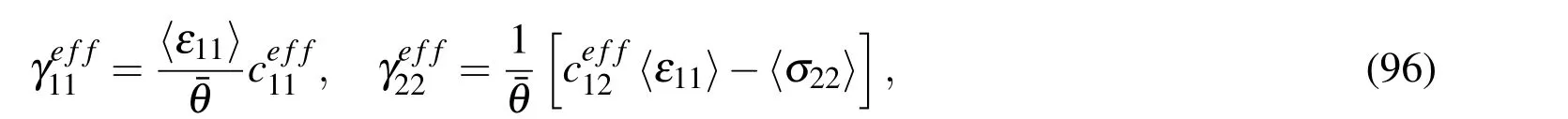
where the average values of the conjugated fields 〈ε11〉,〈σ22〉are given by formulae （84）and （83）,with the integrands being obtained from the solution of the considered boundary value problem.

If boundary conditions are selected as shown in Fig.7,the average values of the secondary fields are given as

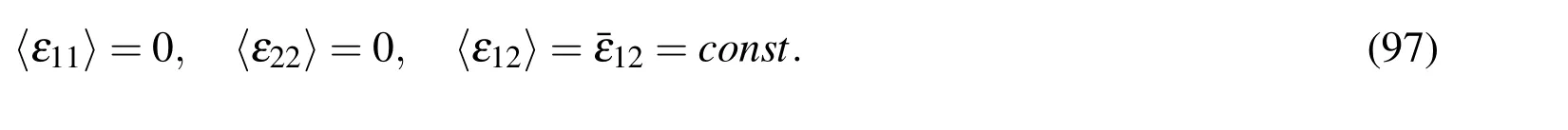
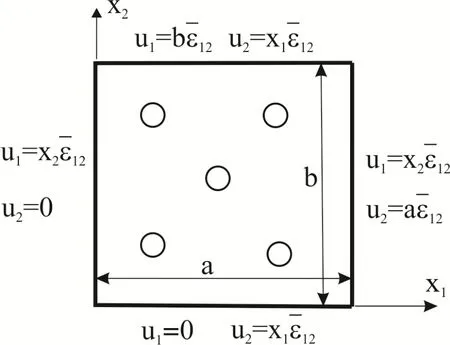
Figure 7:Boundary conditions appropriate for evaluation of

Now,we can calculate the following effective material coefficients

Thus,having solved the above considered boundary value problems in the RVE sample,we can calculate all the effective material coefficients in materials with voids.

6 Numerical examples

6.1 RVE with a single void

In this numerical example it is analyzed one circular void in square domain （a×a）,where various values of void radii are considered.The material parameters corresponding to cadmium selenide ceramic material;they are given by[Li at al.（2015）]:

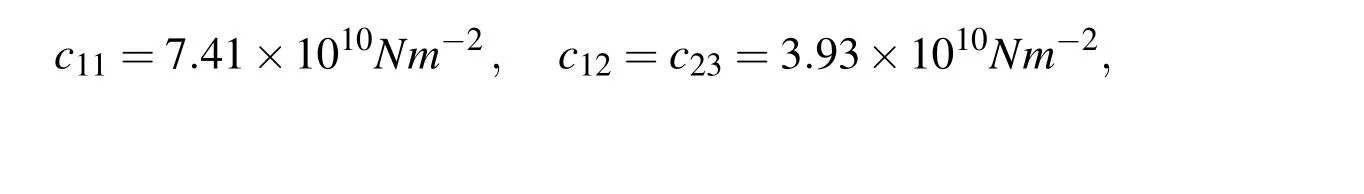
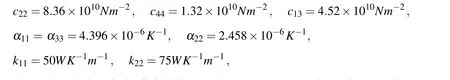
The analyzed domain is divided into polygons and each polygon is treated as a scaled boundary finite element subdomain （see Fig.8）.To have a good visibility from the scale centre on boundaries of the analyzed domain,it is necessary to introduce subdomains for this not simply-connected domain.There are needed at least 4 subdomains to solve this problem.We have considered 12 polygons in numerical analyses（Fig.8）with getting quasi uniform fictitious triangulation which is appropriate for approximation accuracy.Only boundaries of subdomains need to be discretized with line elements.Three nodes elements are used for discretization of subdomain boundaries.There are totaly 108 nodes in this mesh.

Figure 8:Discretization of a square domain with a circular void in the SBFEM.

Figure 9:Variation of effective elastic coefficients c11,c12on porosity.

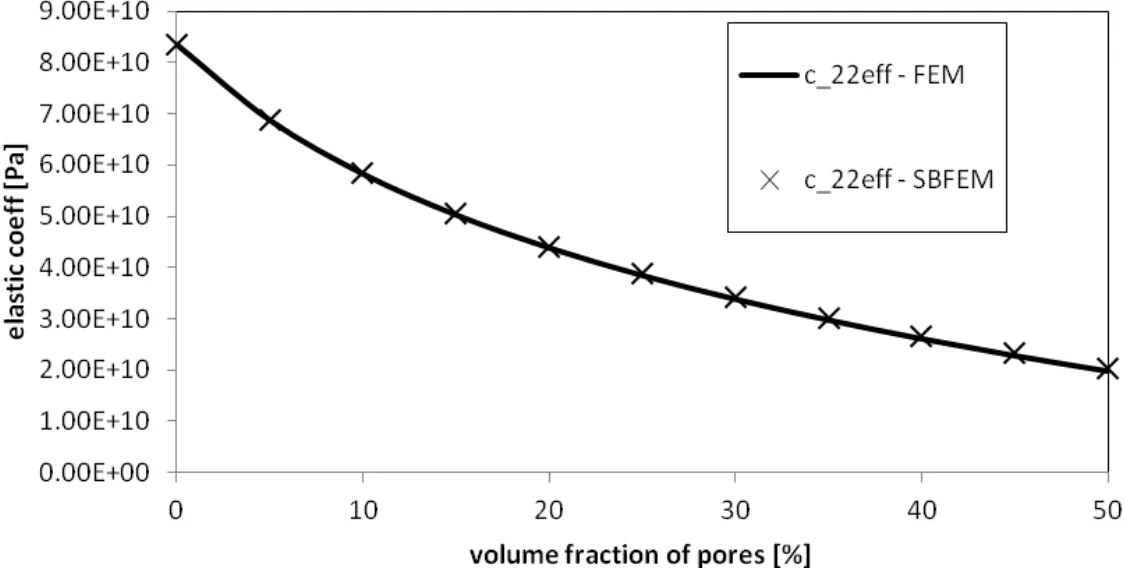
Figure 10:Variation of effective elastic coefficient c22on porosity.

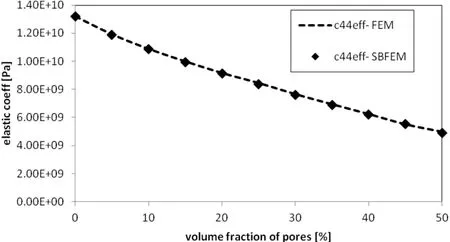
Figure 11:Variation of effective elastic coefficient c44on porosity.

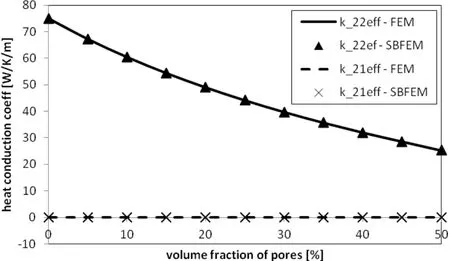
Figure 12:Variation of effective thermal conductivities on porosity.

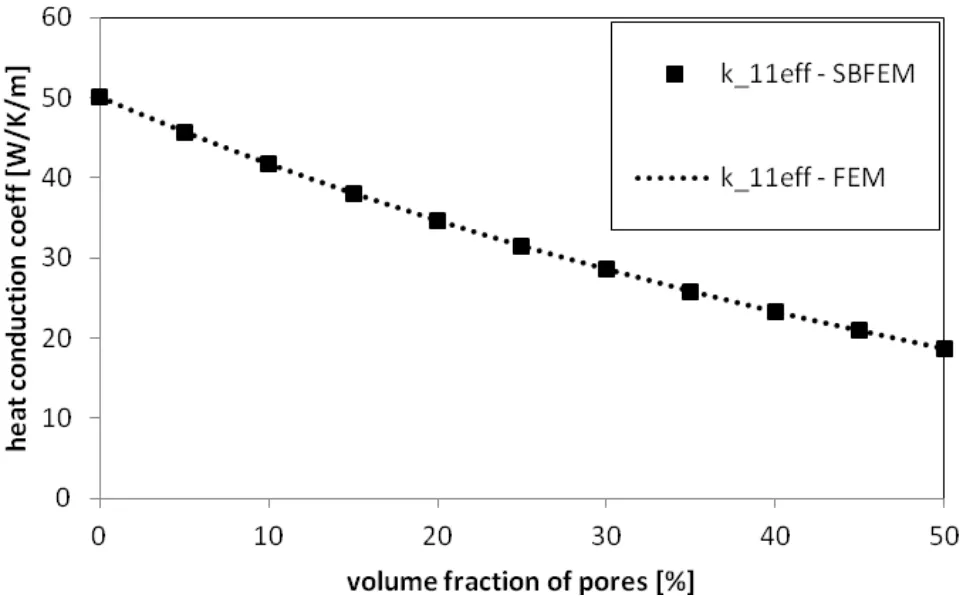
Figure 13:Variation of effective thermal conductivities on porosity.

Figure 14:Variation of effective stress-temperature moduli ity.

6.2 RVE with multiple voids

In order to show the capabilities of present SBFEM formulation,the numerical example considering four circular voids in square domain （a×a）is presented next,where various values of void radii are again considered.The analyzed domain is divided into 33 polygons and each polygon is treated as a scaled boundary finite element subdomain.SBFEM subdomains for volume fraction f=35%are shown in Fig.15.Three node elements are used for discretization of subdomain boundaries.There are totaly 316 nodes in this mesh.In comparison,FEM mesh created in Comsol Multiphysics for the same problem would consist of 6707 quadrilateral elements.

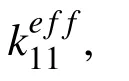
Figure 15:Discretization of a square domain with four circular voids in the SBFEM.

Figure 16:Variation of effective thermal conductivities on porosity for two RVEs.

Figure 17:Variation of effective stress-temperature moduli on porosity for two RVEs.

Figure 18:Variation of effective elastic coefficients c11,c12and c22on porosity for two RVEs.

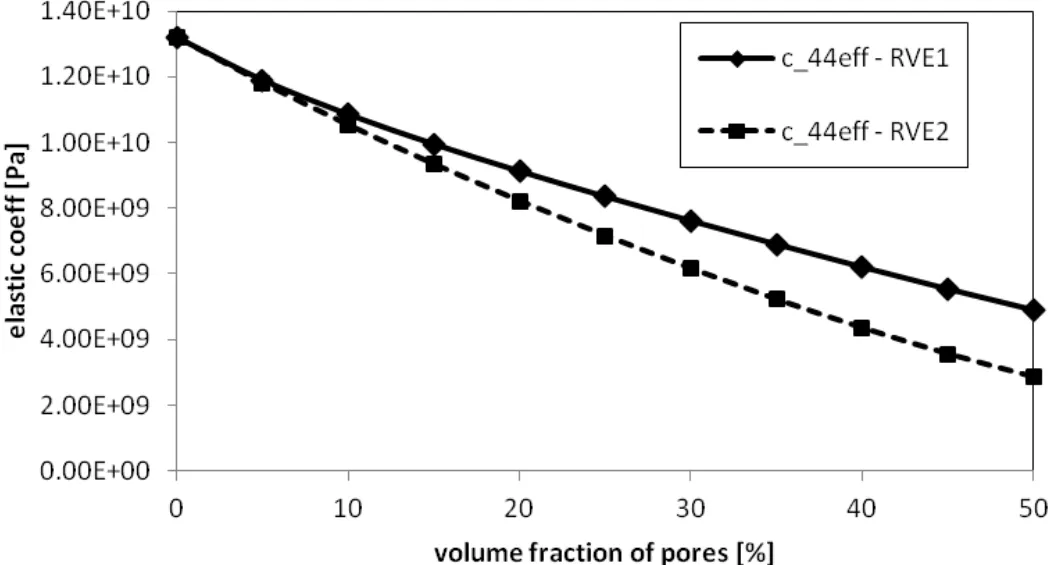
Figure 19:Variation of effective elastic coefficient c44on porosity for two RVEs.

7 Conclusions

The scaled boundary finite element method is applied to solve uncoupled thermoelastic boundary value problems for the RVE to get effective material properties of elastic solids with voids.In the first step the temperature distribution is analyzed by the SBFEM.In the second step the elastic problem with known temperature is solved.The scaled boundary finite element equation is derived,which has a nonhomogeneous form with temperature and its gradients on the right hand side.The eigenvalue method is applied to solve the homogeneous equation and the technique of variation of integration constants is applied to the non-homogeneous system.The average values of the conjugated fields on the RVE are computed for evaluation effective mechanical and thermal coefficients.The numerical results are compared with finite element method （FEM）results and a very good agreement is observed.The mesh is significaly coarser in the SBFEM than in the FEM and a tremendous

reduction in the total number of DOFs is achieved in comparison with the FEM model.The SBFEM is applied to the RVE with multiple voids to demonstrate the relative superiority of the SBFEM with respect to the conventional FEM.

In future work we consider to analyze fiber or particle reinforced compositematerials.In the RVE instead of voids the inclusion material properties have to be considered.On the interface of the matrix and inclusion the continuity for the displacements and temperature,as well as the equilibrium for the tractions and heat fluxes have be taken into account.

Acknowledgement:The authors acknowledge the support by the Slovak Science and Technology Assistance Agency registered under number APVV-14-0216.

Ahmedi,I.;Sheikhy,N.;Aghdam,M.M.;Nourazer,S.S.（2010）:A new local meshless method for steady-state heat conduction in heterogeneous materials.Engineering Analysis with Boundary Elements,vol.34,pp.1105–1112.

Benveniste,Y.（1987）:A new approach to the application of Mori-Tanaka’s theory in composite materials.Mechanics of Materials,vol.6,no.2,pp.147–157.

Bishay,P.L.;Atluri,S.N.（2012）:High-performance 3D hybrid/mixed,and simple 3D Voronoi cell finite elements,for macro-µ-mechanical modeling of solids,without using multi-field variational principles.CMES:Computer Modeling in Engineering&Sciences,vol.84,pp.41-97.

Bohm,H.;Han,W.（2001）:Comparisons between three-dimensional and twodimensional multi-particle unit cell models for particle reinforced metal matrix composites.Modeling Simulation in Material Science and Engineering,vol.9,pp.47–65.

Bohm,H.;Eckschlager,A.;Han,W.（2002）:Multi-inclusion unit cell models for metal matrix composites with randomly oriented discontinuous reinforcements.Computational Material Science,vol.25,pp.42–53.

Budiansky,B.（1965）:On the elastic moduli of some heterogeneous materials.Journal of the Mechanics and Physics of Solids,vol.13,pp.223–227.

Castaneda,P.;Willis,J.（1995）:The effect of spatial distribution on the effective behavior of composite materials and cracked media.Journal of the Mechanics and Physics of Solids,vol.43,pp.1919–1951.

Christensen,R.M.（1993）:Effective properties of composite materials containing voids.Proceedings of the Royal Society A,vol.440,no.1909,pp.461–473.

Chiong,I.;Tat Ooi,E.;Song,Ch.;Tin-Loi,F.（2014）:Computation of dynamic stress intensity factors in cracked functionally graded materials using scaled boundary polygons.Engineering Fracture Mechanics,vol.131,pp.210-231.

Dargush,G.F.;Banerjee,P.K.（1991）:A new boundary element method for three-dimensional coupled problems of conduction and thermoelasticity.ASMEJournal of Applied Mechanics,vol.58,pp.28-36.

Deeks,A.J.;Wolf,J.P.（2002a）:A virtual work derivation of the scaled boundary finite-element method for elastostatics.Computatinal Mechanics,vol.28,pp.489–504.

Deeks,A.J.;Wolf,J.P.（2002b）:An h-hierarchical adaptive procedure for the scaled boundary finite-element method.International Journal for Numerical Methods in Engineering,vol.54,pp.585–605.

Dong,L.;Atluri,S.N.（2011）:A simple procedure to develop efficient&stable hybrid/mixed elements,and Voronoi cell finite elements for macro-µmechanics.CMC:Computers,Materials&Continua,vol.24,pp.61-104.

Dong,L.;Atluri,S.N.（2012）:T-Trefftz Voronoi cell finite elements with elastic/rigid inclusions or voids for micromechanical analysis of composite and porous materials.CMES:Computer Modeling in Engineering&Sciences,vol.83,pp.183-220.

Druma,A.M.;Alam,M.K.;Druma,C.（2004）:Analysis of thermal conduction in carbon foams.International Journal of Thermal Sciences,vol.43,pp.689-695.

El Moumen,A.;Kanit,T.;El Minor,H.（2015）:Computational thermal conductivity in porous materials using homogenization techniques:Numerical and statistical approaches.Computational Materials Science,vol.97,pp.148–158.

Engquist,B.;Li,X.;Ren,W.;Vanden-Eijnden,E.（2007）:Heterogenous multiscale methods:a review.Communication in Computational Physics,vol.2,pp.367–450.

Ghossein,E.;Levesque,M.（2014）:A comprehensive validation of analytical homogenization models:The case of ellipsoidal particles reinforced composites.Mechanics of Materials,vol.75,pp.135–150.

Gordon,F.H.;Turner,S.P.;Taylor,R.;Clyne,T.W.（1994）:The effect of the interface on the thermal conductivity of titanium-based composites.Composites,vol.25,pp.583–92.

Goyheneche,J.M.;Cosculluela,A.（2005）:A multiscale model for the effective thermal conductivity tensor of a stratified composite material.International Journal of Thermophysics,vol.26,pp.191-202.

Gruescu,C.;Giraud,A.;Homand,F.;Kondo,D.;Do,D.P.（2007）:Effective thermal conductivity of partially saturated porous rocks.International Journal of Solids and Structures,vol.44,pp.811–818.

Han,L.S.;Cosner,A.A.（1981）:Effective thermal conductivities of fibrous composites.Journal of Heat Transfer,vol.103,pp.387–92.

Hatta,H.;Taya,M.（1986）:Equivalent inclusion method for steady state heat conduction in composites.International Journal of Engineering Science,vol.24,pp.1159-1179.

Hill,R.（1963）:Elastic properties of reinforced solids:some theoretical principles.Journal of the Mechanics and Physics of Solids,vol.11,no.5,pp.357–372.

Hill,R.（1965）:A self-consistent mechanics of composite materials.Journal of the Mechanics and Physics of Solids,vol.13,pp.213–222.

Jasiuk,I.;Chen,C.;Thorp,M.F.（1994）:Elastic moduli of two dimensional materials with polygonal and elliptical holes.Applied Mechanics Review,vol.47,1S,pp.18–28.

Kachanov,M.（1992）:Effective elastic properties of cracked solids.Applied Mechanics Review,vol.45,pp.304–35.

Kanoute,P.;Boso,D.P.;Chaboche,J.L.;Schrefler,B.A.（2009）:Multiscale methods for composites:A review.Archives of Computational Methods in Engineering,vol.16,pp.31-75.

Kögl,M.;Gaul,L.（2003）:A boundary element method for anisotropic coupled thermoelasticity.Archive of Applied Mechanics,vol.73,pp.377-398.

Lekhnitskii,S.G.（1963）:Theory of Elasticity of an Anisotropic Body,Holden Day,San Francisco.

Li,Ch.;Song,Ch.;Man,H.;Ooi,E.T.;Gao,W.（2014）:2D dynamic analysis of cracks and interface cracks in piezoelectric composites using the SBFEM.International Journal of Solids and Structures,vol.51,pp.2096-2108.

Li,Ch.;Ooi,E.T.;Song,Ch.;Natarajan,S.（2015）:SBFEMforfractureanalysis of piezoelectric composites under thermal load,International Journal of Solids and Structures,vol.52,pp.114-129.

Marur,P.（2004）:Estimation of effective elastic properties and interface stress concentrations in particulate composites by unit cell methods.Acta Materialia,vol.52,pp.1263–1270.

Milton,G.W.（2000）:Mechanics of Composites.Cambridge:Cambridge University Press.

Mori,T.;Tanaka,K.（1973）:Average Stress in the Matrix and Average Elastic Energy of Materials with Misfitting Inclusions.Acta Metallica,vol.21,pp.571–574.

Nowacki,W.（1986）:Thermoelasticity,Pergamon,Oxford.

Pierard,O.;Friebel,C.;Doghri,I.（2004）:Mean-field homogenization of multiphase thermo-elastic composites:a general framework and its validation.Composites Science and Technology,vol.64,pp.1587–1603.

Progelhof,R.C.;Throne,J.L.;Ruetsch,R.R.（1976）:Methods for prediction the thermal conductivity of composite systems:a review.Polymer Engineering and Science,vol.9,pp.615–25.

Qin,Q.H.（2004）:Micromechanics-BE solution for properties of piezoelectric materials with defects.Engineering Analasis with Boundary Elements,vol.28,pp.809-814.

Sevostianov,I.;Kachanov,M.（2003）:Connection between elastic moduli and thermal conductivities of anisotropic short fiber reinforced thermoplastics:theory and experimental verification.Materials Science and Engineering A,vol.360,pp.339–44.

Shiah,Y.C.;Tan,C.L.（1999）:Exact boundary integral transformation of the thermoelastic domain integral in BEM for general 2D anisotropic elasticity.Computational Mechanics,vol.23,pp.87-96.

Shiah,Y.C.;Lee,Y.M.;Huang,T.C.（2014）:A novel approach to identify the thermal conductivities of a thin anisotropic medium by the boundary element method.CMC:Computers,Materials&Continua,vol.39,pp.49-71.

Sladek,V.;Sladek,J.（1984）:Boundary integral equation method in thermoelasticity.Part I:General analysis.Applied Mathematical Modelling,vol.7,pp.241-253.

Song,Ch.;Wolf,J.P.（1999）:Body loads in scaled boundary finite-element method.Computer Methods in Applied Mechanics and Engineering,vol.180,pp.117-135.

Song,Ch.（2004a）:A matrix function solution for the scaled boundary finiteelement equation in statics.Computer Methods in Applied Mechanics and Engineering,vol.193,pp.2325-2356.

Song,Ch.（2004b）:A super-element for crack analysis in the time domain.International Journal for Numerical Methods in Engineering,vol.61,pp.1332-1357.

Suh,I.G.;Tosaka,N.（1989）:Application of the boundary element method to 3-D linear coupled thermoelasticity problems.Theoretical and Applied Mechanics,vol.38,pp.169-175.

Wu,T.;Temizer,I.;Wriggers,P.（2013）:Computational thermal homogenization of concrete.Cement&Concrete Composites,vol.35,pp.59–70.

Wu,Y.T.;Nie,Y.F.;Yang,Z.H.（2014）:Comparison of four multiscale methods for elliptic problems.CMES:Computers Modeling in Engineering&Sciences,vol.99,pp.297-325.

1Institute of Construction and Architecture,Slovak Academy of Sciences,84503 Bratislava,Slovakia.Telephone/fax number:+421-54773548;E-mail:jan.sladek@savba.sk