Analytical Method for Simulation of Buckling and Post-buckling Behaviour of Curved Pates

Joo Shin Parkand Jung Kwan Seo

Analytical Method for Simulation of Buckling and Post-buckling Behaviour of Curved Pates

Joo Shin Park1and Jung Kwan Seo2,3

Ships,ship-shaped offshore structures,land-based structures and aerospace structures typically consist of various curved plate components.It is difficult to simulate the buckling and post-buckling of curved thin and/or thick plates that have characteristics of nonlinear structural mechanics,such as nonlinear behaviour when loading is applied.The elastic post-buckling behaviour of a curved plate is very complex,and accompanied by mode changes due to the occurrence of secondary buckling behaviour.Therefore,it is very important to clarify the elastic post-buckling behaviour when subjected to axial loading.The aim of this study was to derive an analytical calculation based on the formulation of the total potential energy,andamathematicalsolutiontosimulatetheelasticbucklingandpost-buckling behaviour of cylindrically curved plates under axial compression.The accuracy of the proposed method with the aforementioned modelling techniques was verified through comparison with finite element analyses of various curved plate configurations.

Cylindrically curved plate,axial compression,buckling strength,post-buckling behavior,secondary buckling.

Nomenclature

a Length of plate

b Breadth of plate

D Flexible rigidity of plate （=Et3/12（1-v2））

E Young’s modulus

F Airy’s stress function

m,n Maximum half-waves number of the assumed added deflection function in the x and y directions,respectively

R Radius of curvature of cylindrically curved plate

riArc length at step i

t,tpPlate thickness

w Added deflection of plate due to action of external loads

w0Initial deflection of plate

x,y,z Principal axes

εclStrain of flat plate

εcrStrain of curved plate

εxb,εybBending strains in the x and y directions,respectively

σclElastic buckling strength of flat plate

σcrElastic buckling strength of curved plate

σxNormal stress in the x direction （compressive stress）

σxb,σybBending stresses in x and y directions,respectively

σYYield stress

τ=τxyShear stress

ν Poisson’s ratio

1 Introduction

Curvedplatesareusedinvariouspartsofshipsandoffshorestructures（deckplating with a camber,fore and aft parts,bilge parts,gunwale parts,etc.）and in various civil engineering structures（web panels in horizontally curved steel plates,box girder bridges,etc.）.In ship structural design,accurate prediction of the structural behaviour of curved plates is a most important step,as the shape of the hull is critical to the overall strength performance of a ship.The structural performance of a curved plate is influenced by different types of failure modes,and the ultimate and buckling strength and structural behaviour must be investigated for structural design.

A number of researchers have made important contributions in this area by developing numerical,experimental and analytical approaches for investigating structural behaviour[Maeno,Yamaguch,Fujii,and Yao （2004）;Park,Kohei,Shinsuke,Iijima,and Yao （2006）;Park,Iijima,and Yao （2008）;Kwen,Park,Paik,and Lee,（2004）;Cho,Park,Kim,and Seo （2007）;Levy （1943）;Dai,Paik,and Atluri（2011）].Buckling behaviour associated with the plastic collapse behaviour of unstiffened and stiffened curved plates is also well documented in the literature[Park （2008）].

The elastic post-buckling behaviour of curved plates sometimes occurs as secondary buckling behaviour.Simulation of this phenomenon is highly complex using a nonlinear analytical solution accompanied by mode change.This occurrence is related to thin rather than thick plates,according to previous research[Kim,Kim,and Lee （2004）;Hao,Cho,and Lee （2000）].In ship structures,the curved plates tend to be thick,so that plastic buckling takes place but elastic buckling does not.However,recent design concepts tend to favour bigger ships with optimised structural scantling for greater lightness and speed.This means that thick plates can be treated as thin plates from a geometrical point view;thus it is necessary to simulate the elastic post-buckling behaviour,which is considered to be secondary buckling when subjected to axial loads.

During the motion of a ship through extreme waves,bending of the hull girders can produce axial loading on the curved plates.It is well known that curvature increases the buckling strength of a circular cylinder subjected to axial loading.At the same time,plates with curvature are expected to increase not just the buckling strength but also the ultimate strength.To simulate the influence of curvature on the buckling and post-buckling behaviour of cylindrically curved plates,the structural phenomena must be identified through a series of elastic large deflection analyses andelasticeigenvalueanalysis.Atthebeginning,elasticeigenvalueanalysisshould be performed on a cylindrically curved plate under axial compression to clarify the influence of curvature on elastic buckling strength.To develop an analytical formulation,fundamental equations should be derived involving elastic large deflection analysis.

Some researchers have successfully simulated the geometrically nonlinear postbuckling behaviour of unstiffened cylinders,stiffened cylindrical panels and laminated composite double curved shells using commercial finite element（FE）code and a semi-analytical solution[Guggenberger（1995）;Buermann,Rolfes,Tessmer,and Schagerl（2006）;Kundu and Shinha （2007）].However,although the finite element analysis（FEA）method is a powerful tool for simulating the behaviour of complex structures under extreme loads,this may require a great deal of modelling and computational effort.Moreover,there is limited information for developing an analytical method to simulate both snap-though and snap-back post-buckling behaviour accompanied by mode change.

The paper proposes to clarify these issues.Fundamental equations are derived for elastic large deflection analysis to simulate the elastic buckling and post-buckling behaviour of cylindrically curved plates under axial compression.An explicit buckling solution is obtained from a formulation of the total potential energy for cylindrically curved plates.The accuracy of the proposed method is verified by comparing its results with that of FEA code.

2 Elastic large deflection analysis of cylindrically plates by the energy method

The system examined,shown schematically in Figure 1 is a beam of variable cross section,This study reports an accurate energy method-based solution for the elastic post-buckling behaviour of cylindrical plates subjected to axial compression.The analytical method uses Kirchhoff’s thin plate theory with the following assumptions:（a）the material is linear elastic,homogeneous and isotropic;（b）the plate is a perfect plane and stress free;（c）the thickness“t”of the plate is small compared to its other dimensions;（d）the in-plane actions pass through its middle plane;（e）the transverse displacements“w”are small compared to the thickness of the plate;（f）the slopes of the deflected middle surfaces are small compared to unity;（g）the deformations are such that straight lines,initially normal to the middle plane,remain straight and normal to the deflected middle surface;（h）the stresses normal to the thickness of the plate are of negligible magnitude;and （i）the distortion due to transverse shearing can be ignored.

The method developed and proposed here derives and expresses an explicit solution for the simulation of post-buckling behaviour.For this purpose,the method derivation is combined with the arc-length increment method.

2.1 Initial deflection mode

The cylindrically curved plate shown in Figure 1 is considered.All edges are assumed to be simply supported and kept in a straight line when subjected to in-plane movements.The initial deflection of the following form of the Fourier series is assumed.

The total deflection under axial compression is assumed to be represented by the same components as those of the initial deflection,that is

where b=Rχ,y=Rθ

The coordinate system and dimensions of a curved plate under axial compression are shown in Figure 1.Here u,v,w denote the displacement components in the x,y and z directions,respectively,at the middle surface,and wodenotes the initial deflection.According to Timoshenko and Gere （1961）,the in-plane strain compo-nents due to small displacements are represented as

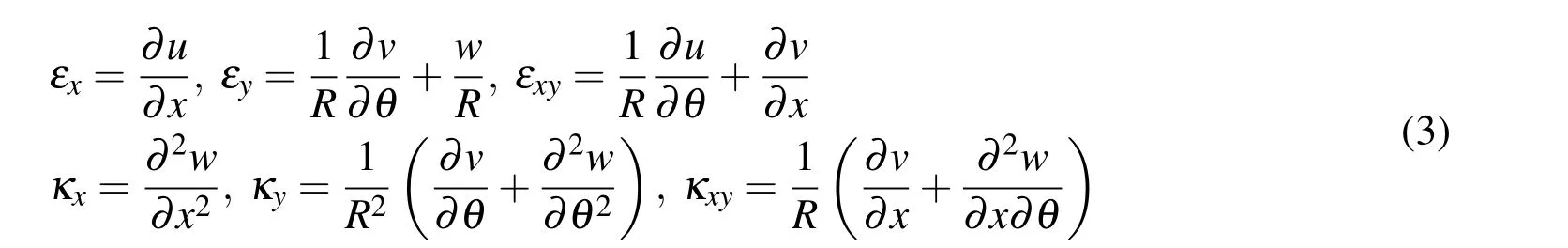
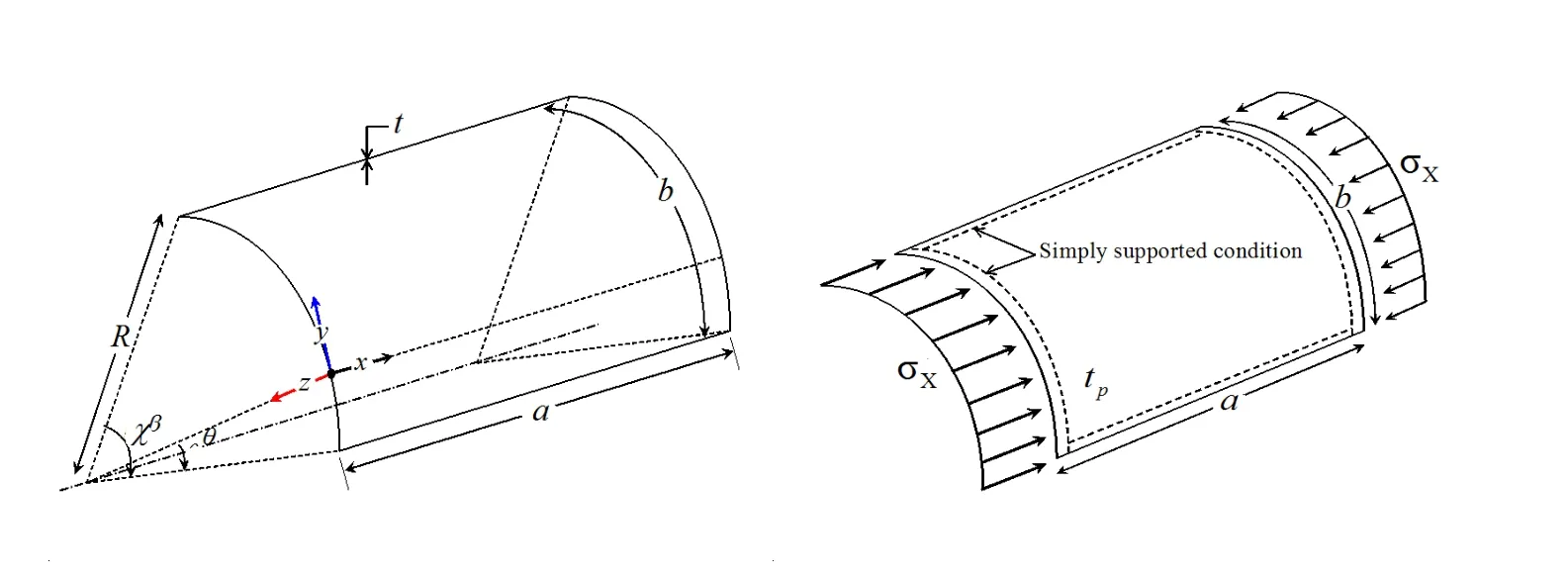
Figure 1:Cylindrically curved plate under axial compression.

These expressions are the same as the well-known expressions for the case of a flat plate,with the addition of w/R to the expression for εy.This term is due to the change in radius,which produces the strain.

2.2 Equilibrium and compatibility equations

The fundamental equations governing the deflection of thin curved plates were developed by Donnell（1934）.By differentiation and combination of the equations,the compatibility equation becomes

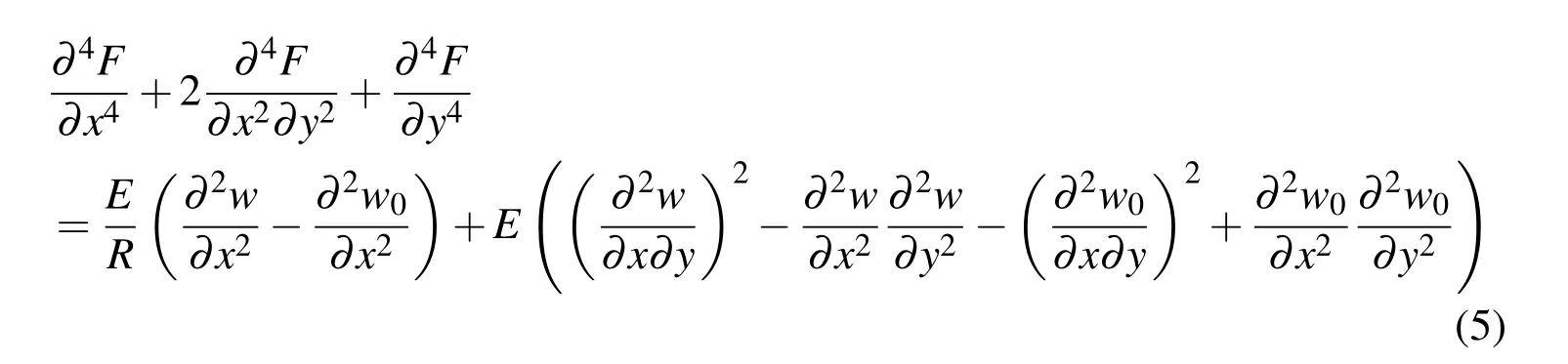
The in-plane stress components are derived as follows.

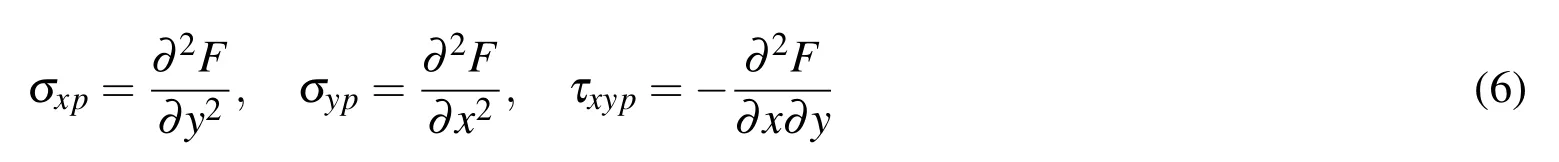
Assuming the plane stress state,the in-plane strain components are derived as follows,

where E is the Young’s modulus and ν is the Poisson’s ratio.

2.3 Bending strain and stress components

The bending strain components are expressed in the following forms.

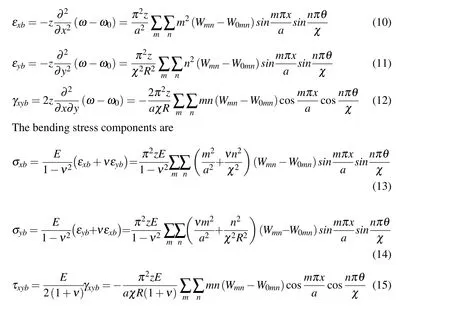
2.4 In-plane strain displacement relationships

Given that large deflections are considered,nonlinear strain displacement relationships are used[von Karman and Tsien （1941）].The membrane strain can be written as Equation （16）,where w and woare the additional and initial out-of-plane deflection of the curved plate,respectively.Denoting displacements in the x,y and z directions as u（x,y,z）,v（x,y,z）and w（x,y,z）,respectively,the in-plane strain displacement relationships are expressed as follows.

Where Equation （16）takes the derivative with respect to x,the end-shortening displacement is obtained as follows

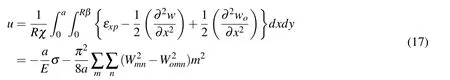
where aRχ is（m-k=0 and n-l=0）and 4aRχ/mnπ2is（m,n=odd numbers）.

The average in-plane strain in the loading direction is evaluated by dividing Equation （17）by length a,and given as follows.

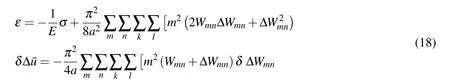
2.5 Application of the principle of virtual work

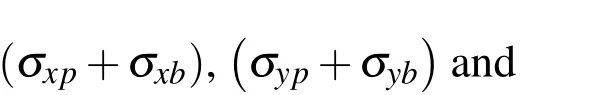
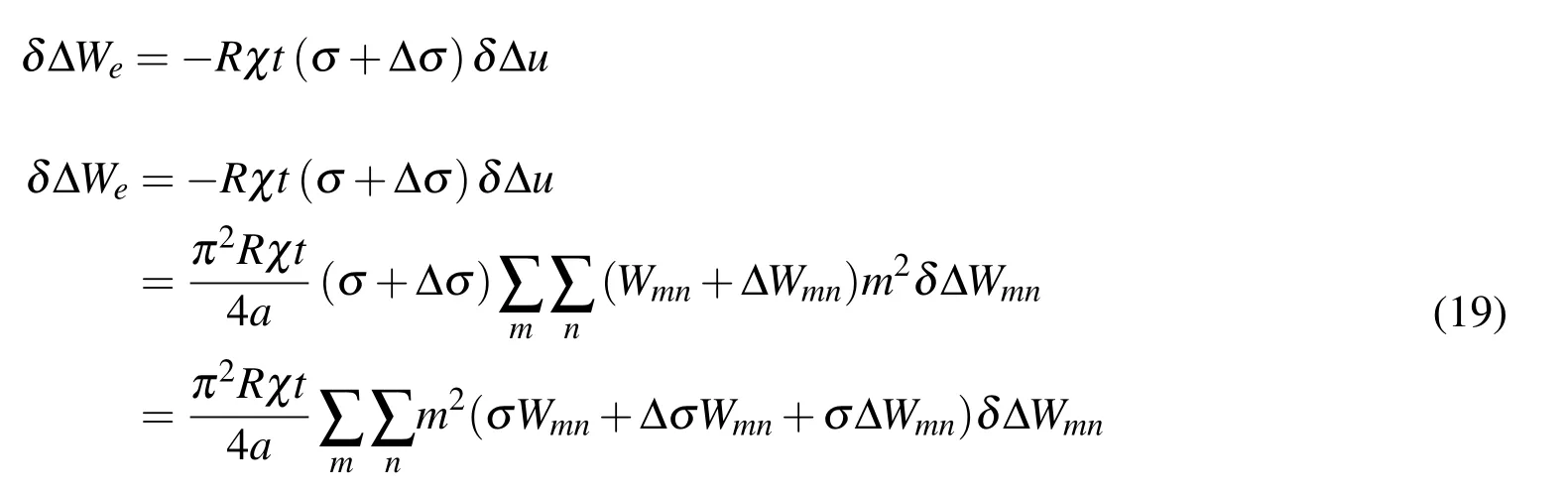
However,the virtual work by the internal force is expressed as

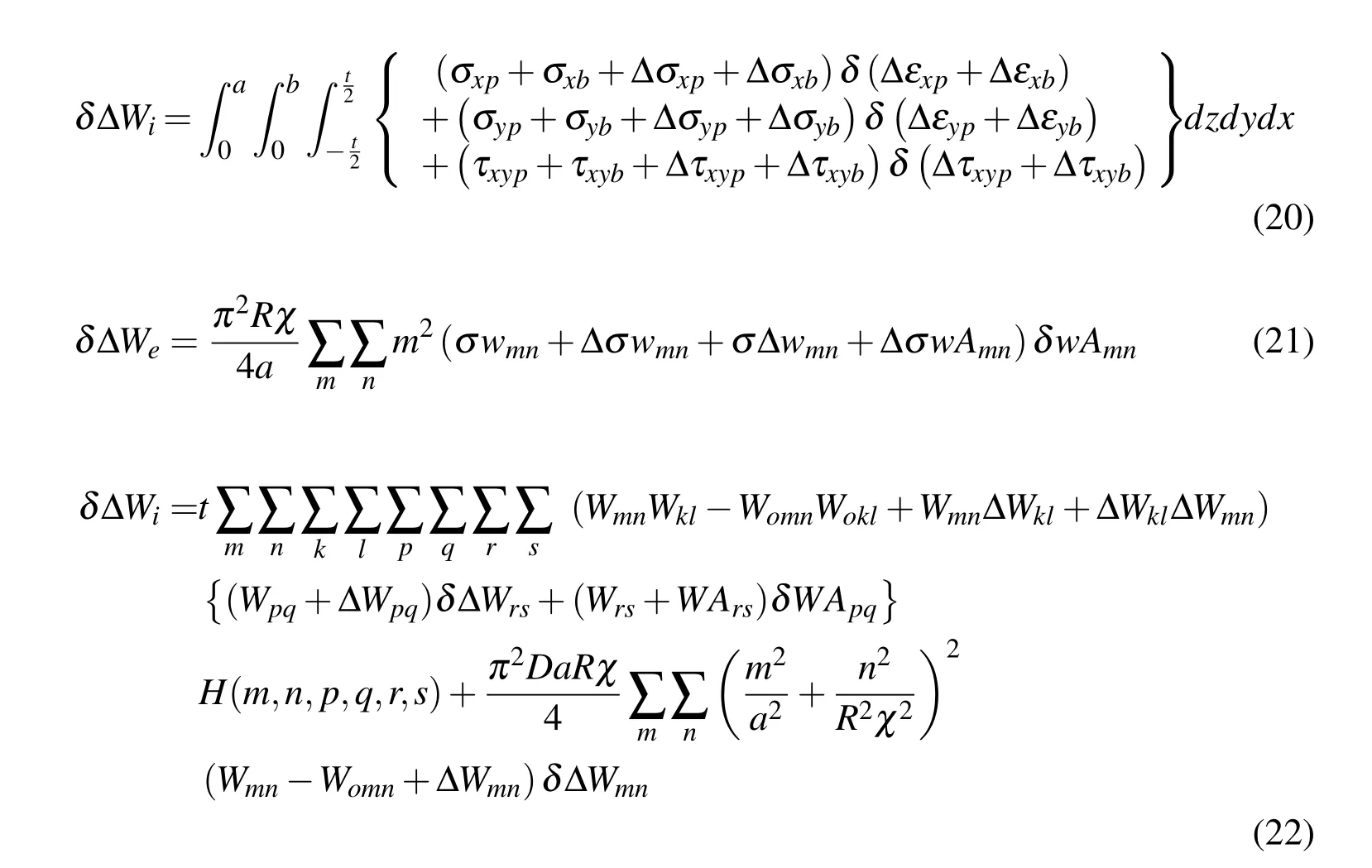
In this manner,adoption of the principle of virtual work is written in the following form.

Equation （24）can be represented as follows.

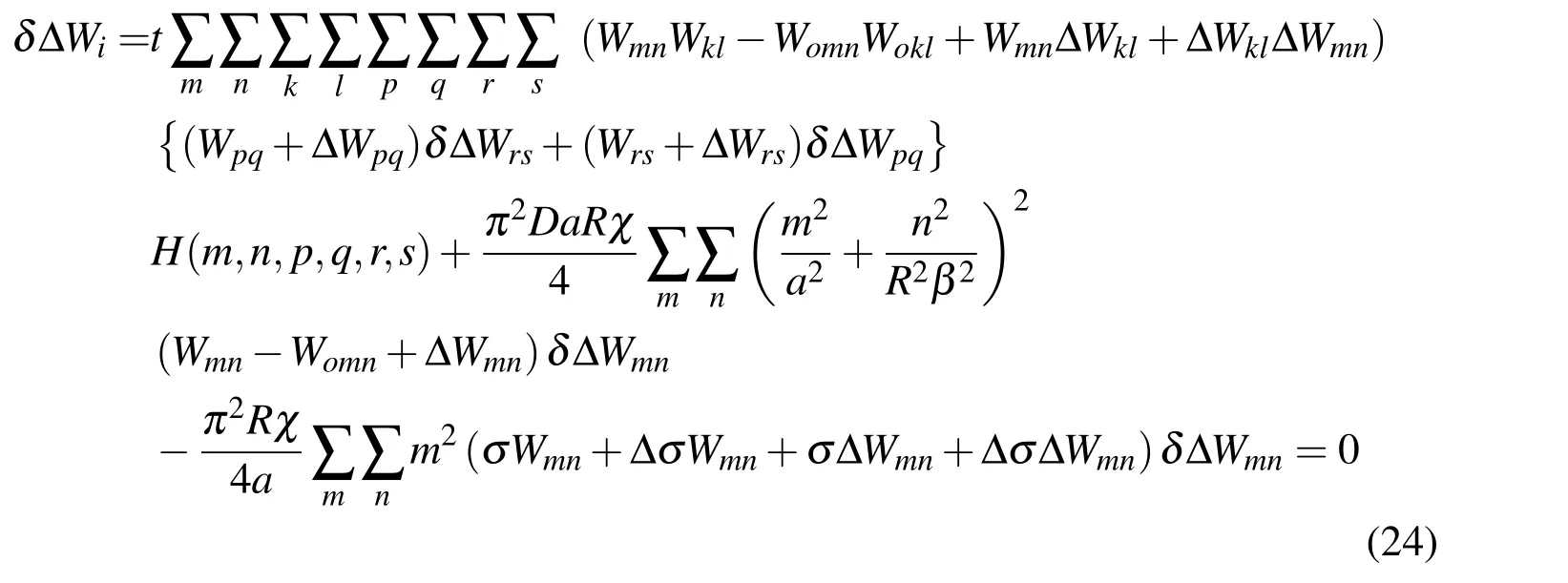
Where coefficients H （m,n,k,l,p,q,r,s）represent the dimensions of the plate,elastic modulus,half waves number,theseare functions from m to s.Inthe previous equation,we derived the relationships of the coefficients of bending ΔWmnand the increment of the average compressive stress.This relationship can be represented by inducing a first order equation about the bending coefficient of the increments

where{ΔW}represents the increment of bending

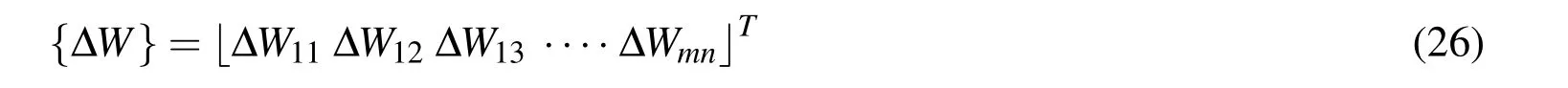
Δσ{R}is the external increment and{R}is a function of the deflection coefficients Wmnand Womn,respectively.The term{Q}is used to modify the unbalanced force induced by linear approximation during the increment.

2.6 Increments using the arc-length method

Step i-1 can be represented as

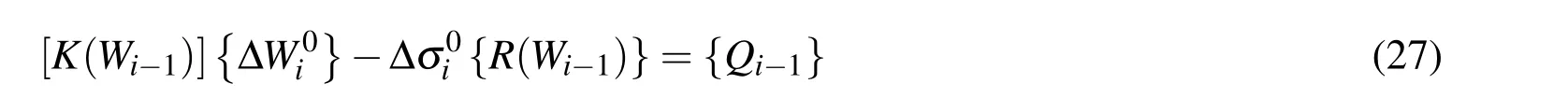
Then the arc length must satisfy the following relation,

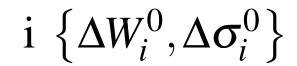
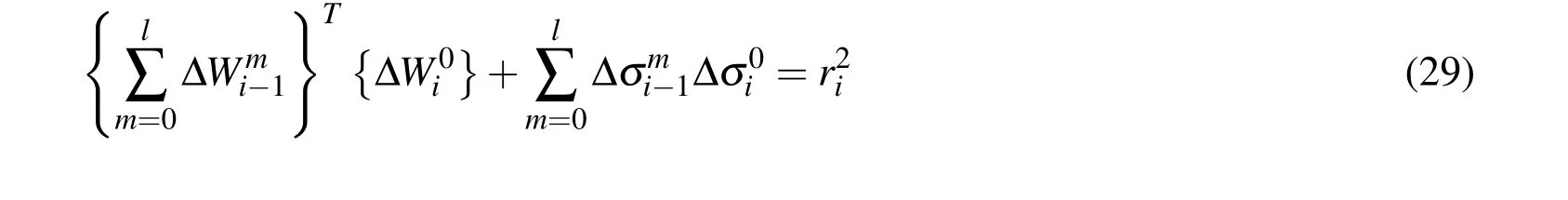
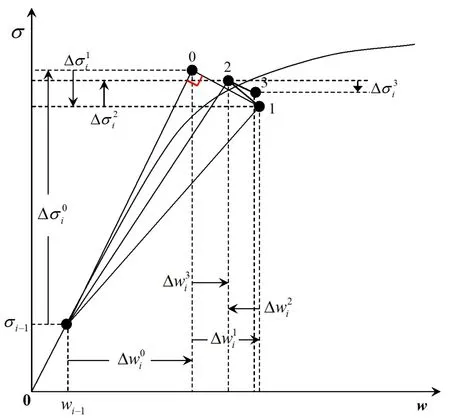
Figure 2:Arc-length increment method.

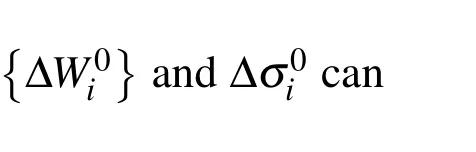
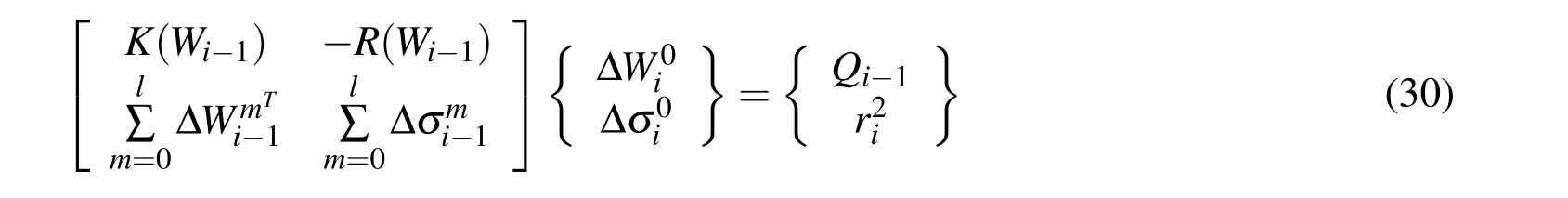
During the repeat and convergence calculations of step n,we can represent the stiffness matrix equation as

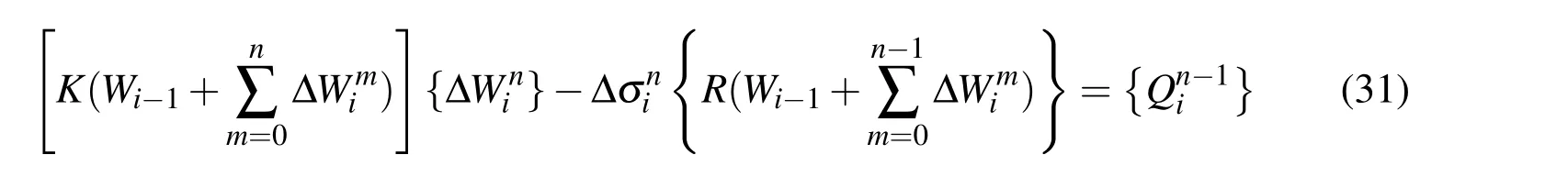
The arc length （ri）needed to satisfy the same length can be represented as

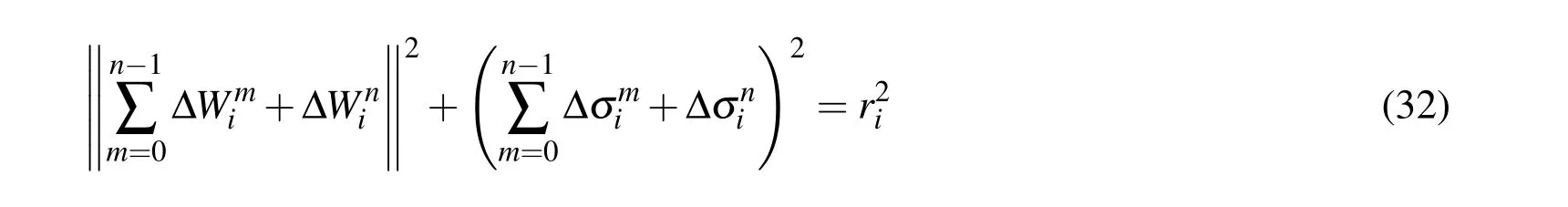
Equation （32）can be linearised as shown.

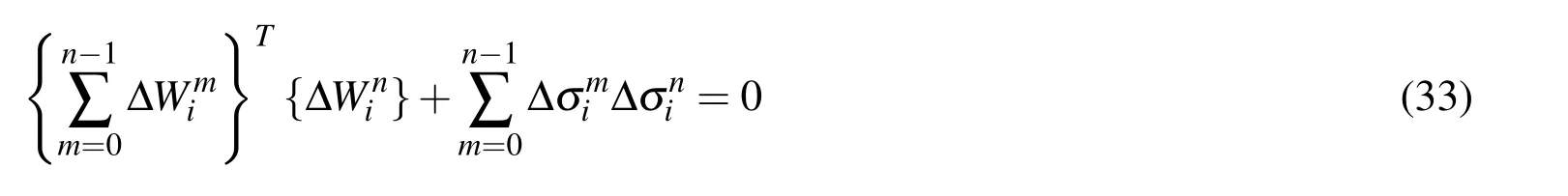
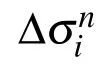
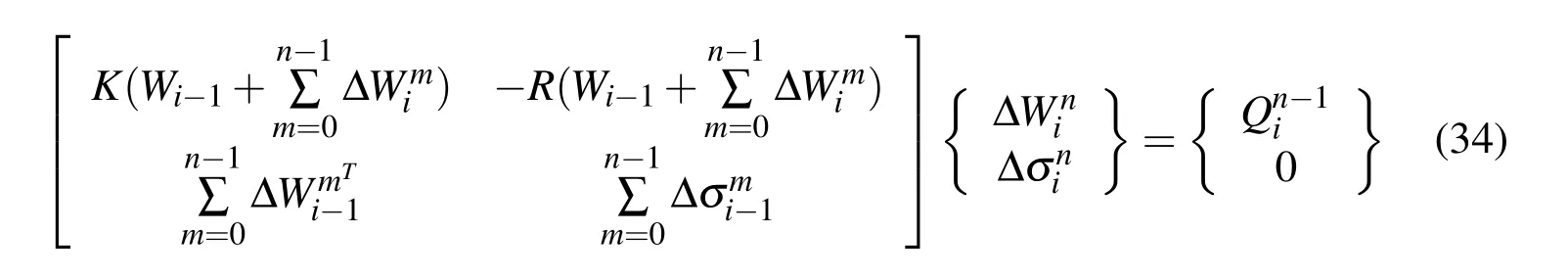
In this calculation,equation （34）is repeated until the non-parallel force{Qi}is equal to zero.

3 Verification of the analytical method

3.1 Investigation of curvature and slenderness ratio of commercial ship structures

Before calculation,we investigated the curvature and slenderness ratios for actual ship structures.Figure 3 shows the curvature and slenderness ratios from investigations of several kinds of ships.The bilge structure of a tanker and bulk carrier has a curvature ranging from 2,000 to 2,500 mm.However,container ships have a larger curvature due to the increased length of these ships,ranging from 3,500 to 6,500 mm.The slenderness ratio ranges from 1.4 to 3.0 around the bilge structure and midship section.In the present paper,the range of design parameters for the calculations were based on the investigation of real data.

3.2 Verification of the analytical method

To demonstrate the accuracy and validity of the proposed analytical method,the elastic buckling strength of curved plates was computed using both the proposed energymethodandFEAprograms[ANSYS （2013）].Fortheelasticlargedeflection analyses,the FEM code ANSYS was used with the shell 181 element,which is suitable for analysing thin to moderately thick shell structures.This element is a four-noded Reissener-Mindlin shell element with six degrees of freedom at each node and is applicable to simulate large strain behaviour.The arc-length method was applied in conjunction with the modified Newton-Raphson method in both standard and modified forms.

Figure 3:Investigation of curvature and slenderness ratios in ship structures.

To examine the rationality of the proposed model,a series of calculations was carried out changing the aspect ratio,slenderness ratio and curvature.Typical average stress–average strain relationships are shown in Figures 4 and 6 （A）,（B）,（C）and（D）,respectively.The solid line with symbols indicates the results of FEM and the isolated solid line shows the results of the analytical method.Figure 4 shows the relationships between average stress and average strain of a curved plate with flank angles of 5 and 20 degrees and varying plate thickness under axial compression.The unloading behaviour of a thin-walled curved plate with a flank angle of 5 degrees showed a change of de flection after primary buckling under axial compression,as indicated in Figures 4 （A）and 6 （A）,respectively.When small load increments are applied to the curved plate,the middle surface compressive stress builds up and then suddenly releases the internal strain energy in the form of external work done,causing secondary buckling behaviour.The secondary buckling is generally accompanied by snap-through or snap-back buckling phenomena with changing deflection shape.This is the most difficult problem in nonlinear structural analysis.For most practical problems,it is unnecessary to find such uncertain loads and deflection paths.In most cases,the analysis of buckling and post-buckling behaviour using FEM can follow the unloading path using the arc-length method.However,using the analytical method it did not occur,so slightly different buckling stress is shown.The post-buckling behaviour shows good correlation between the FEM and analytical methods.Figure 4 （B）shows an increase in thickness with the same flank angle.Increasing the plate thickness also rapidly increases buckling strength,and unloading behaviour was not observed.When the increased flank Figure5showstherelationshipbetweentheaveragestressandaveragestraincurves for elastic large deflection analysis under axial compression.The plate thickness is taken as 10 and 20 mm,the aspect ratio considered is 3.5,and the maximum magnitude of initial deflection is 0.1%of plate thickness.Two kinds of calculation angle,elastic buckling strength also increased and cylindrical buckling deflection took place at the loading edges,as shown in Figures 4 （C）and 6 （B）,respectively.Figure 4 （D）shows a thick curved plate with almost perfectly linear elastic buckling behaviour.arecomparedforvalidation.Thepre-bucklingbehaviourofthecylindricallycurved plate is approximately linear just before buckling occurs.The curved plate with a flankangleof5degreesshowsslightlydifferentpost-bucklingbehaviouraroundthe occurrence of primary buckling,but the overall behaviour appears similar to that indicated in Figures 6 （A）and 6 （C）,respectively.The pre-buckling behaviour of the cylindrically curved plate is approximately linear just before buckling occurs.It is interesting to see that the buckling and post-buckling behaviour is well predicted by both the analytical and FEM methods.Figure 7 shows the distribution of elastic buckling stresses against varying flank angles for a cylindrically curved plate subjected to axial loading.When the flank angle increases,buckling stress increases to almost linear behaviour.Although some differences are observed in the case of a thin curved plate with a small flank angle,the agreement between results calculated by the proposed analytic method and FEM is considered satisfactory.This is evidence that the analytical formulation is sufficiently accurate compared to the FEM method.

Figure 4:Comparison of calculated results （a/b=3.0,flank angle=5 degrees）.

Figure 5:Comparison of calculated results（a/b=3.5）.

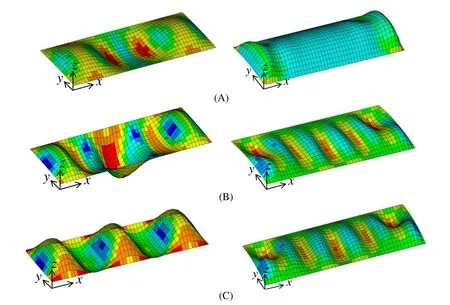
Figure 6:Comparison of buckling deflection at each check point obtained by FEM（a/b=3.0）,（left）t=10 mm,flank angle=5 degrees,（right）t=10 mm,flank angle=20 degrees.

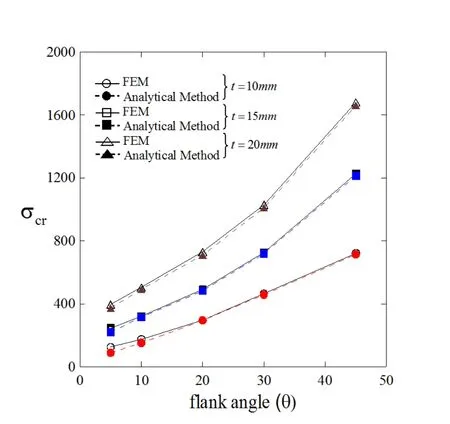
Figure 7:Relationships between elastic buckling stress and flank angle at varying plate thicknesses;comparison of FEM and analytical methods（a/b=3.0）.

4 Conclusions remarks

This paper proposed to clarify the simulation of elastic buckling and post-buckling behaviour with secondary buckling.Fundamental equations were derived for elastic large deflection analysis to simulate the elastic buckling and post-buckling behaviour of cylindrically curved plates under axial compression.An explicit bucklingsolutionwas obtained fromaformulationofthetotal potentialenergyforcylindrically curved plates.The accuracy of the proposed method was verified by comparing its results with those of FEA code.

The calculated results found that the elastic primary buckling strength of a cylindrically curved plate increases with an increase in flank angle.After the occurrence of primary elastic buckling,buckling deformation increases with reduced axial rigidity.Secondary buckling then follows.After the secondary buckling,the equilibrium path is unstable,so that both axial load and displacement decrease with changes in buckling shape.This equilibrium path can be simulated by applying the arc-length method.

The analytical method derived here can be adopted as a basis for an advanced theoretical method to predict the nonlinear buckling strength of a curved plate with varying flank angles and thickness configurations.It is recommended that this solution be used to determine the elastic and post-buckling strength of curved plates,with no need for more complex FEA programs.

Acknowledgement:This work was supported by a 2-Year Research Grant of Pusan National University.

ANSYS（2013）:User’s Theory Manual V15.0（2013）,Chapter Four,Introduction to material nonlinearities.ANSYS Inc.

Buermann,P.;Rolfes,R.;Tessmer,J.;Schagerl,M.（2006）:A semi-analytical model for local post-buckling analysis of stringer and frame-stiffened cylindrical panels.Thin-Walled Structures,vol.44,pp.102-114.

Cho,S.R.;Park,H.Z.;Kim,H.S.;Seo,J.S.（2007）:Experimental and numerical investigations on the ultimate strength of curved stiffened plates.Proceedings of 10th International Symposium on Practical Design of Ships and other Floating Structures,Houston,Texas,USA.

Donnell,L.H.（1934）:A new theory for the buckling of thin cylinders under axial compression and bending.Transactions ASME,vol.56,pp.795-806.

Hao,B.;Cho,C.;Lee,S.W.（2000）:Buckling and post-buckling of soft-core sandwich plates with composite facesheets.Computational Mechanics,vol.25,no.5,pp.421-429.

Dai,H.;Paik,J.K.;Atluri,S.N.（2011）:The Global Nonlinear Galerkin Method for the Analysis of Elastic Large Deflections of Plates under Combined Loads:A Scalar Homotopy Method for the Direct Solution of Nonlinear Algebraic Equations.Computers,Materials&Continua,vol.23,no.1,pp.69-100.

Guggenberger,W.（1995）:Buckling and post-buckling of imperfect cylindrical shells under external pressure.Thin-Walled Structures,vol.23,pp.351-366.

Kim,J.;Kim,Y.H.;Lee,S.W.（2004）:Asymptotic Postbuckling Analysis of Composite and Sandwich Structures via the Assumed Strain Solid Shell Element Formulation.CMES:Computer Modeling in Engineering&Sciences,vol.6,no.3,pp.267–276.

Kundu,C.K.;Shinha,P.K.（2007）:Post buckling analysis of laminated composite shells.Composite Structures,vol.78,pp.316-314.

Kwen,Y.W.;Park,Y.I.;Paik,J.K.;Lee,J.M.（2004）:Buckling and ultimate strength characteristics for ship curved plate structures.Proceedings of the Annual Autumn Meeting of SNAK,Sancheong,Korea.

Levy,S.（1943）:Large-deflection theory of curved sheet.National Advisory Committee for Aeronautics,Technical Note No.895.

Maeno,U.;Yamaguch,H.;Fujii,Y.;Yao,T.（2004）:Buckling/plastic collapse behaviour and strength of bilge circle and its contribution to ultimate longitudinal strength of ship’s hull girder.Proceeding of the 14th International offshore and polar engineering conference,Toulon,France.

Park,J.S.（2008）:Buckling/plastic collapse behaviour of unstiffened and stiffened curved plates.Thesis forthe degree of Doctor of Engineering,Department of Naval Architecture and Ocean Engineering,Osaka University,Japan.

Park,J.S.;Kohei,Y.;Shinsuke,K.;Iijima,K.;Yao,T.（2006）:Buckling and post-buckling behaviour of cylindrically curved plates under axial compression.Proceedings of the Society of Naval Architects and Ocean Engineers,Japan.

Park,J.S.;Iijima,K.;Yao,T.（2008）:Characteristics of buckling and ultimate strength and collapse behaviour of cylindrically curved plates subjected to axial compression.Applied Mechanics and Materials,pp.1195-1200.

Timoshenko,S.P.;Gere,J.M.（1961）:Theory of elastic stability.McGraw Hill Kogakusha Ltd.UK.

VonKarman,T.;Tsien,H.S.（1941）:Thebucklingofthincylindricalshellsunder axial compression.Journal of the Aeronautical Sciences,vol.8,no.8,pp.303.

1Marine Research Institute,Samsung Heavy Industries Co.,Ltd.,Geoje 656-710,Republic of Korea.Ph.D.,E-mail:jooshin.park@samsung.com

2TheKoreaShipandOffshoreResearchInstitute（TheLloyd’sRegisterFoundationResearchCentre of Excellence）,Pusan National University,Busan 609-735,Republic of Korea.

3Corresponding author.Professor,E-mail:seojk@pusan.ac.kr