城市轨道交通工程平面控制测量坐标系统投影面转换方法的应用研究

银志敏，王 军，马全明，李建青，张华海

(1.徐州市勘察测绘研究院，江苏徐州221018;2.北京城建勘测设计研究院有限责任公司，北京100101;3.中国矿业大学，江苏徐州221008)

一、引 言

近年来我国城市轨道交通事业的发展日新月异，进入了一个快速发展期。城市轨道交通工程是一个结构复杂的综合工程，是集地下、地面和高架于一体的快速轨道交通系统。城市轨道交通工程建设与一般的市政和工民建工程建设项目相比有共同之处，但也有其特殊性，对测量工作的要求也更为严格。地面平面控制测量是城市轨道交通工程所有测量工作的基础和依据，是城市轨道交通工程全线线路与结构贯通的保障。由于城市轨道交通建设与城市各类市政工程建设密不可分，工程设计所需的测量资料要互相利用，城市轨道交通工程建设中的测量工作需与之相统一。因此，国家标准《城市轨道交通工程测量规范》也明确要求，轨道交通工程平面控制网的坐标应与所在城市现有坐标系统一致;投影面高程与城市现有坐标系统投影面高程一致，若轨道面平均高程与城市投影面高程的高差影响大于5 mm/km时，应采用其线路轨道的平均高程作为投影面高程。

二、地面或轨道面上长度投影到高斯平面上的变形分析

按高斯正形投影6°分带或3°分带所建立的高斯平面坐标系统通常称为国家统一坐标系统。高斯投影会引起长度变形，工程测量采用国家统一坐标系统时，控制网实测边长应换算为高斯平面边长，地面长度换算为高斯平面边长要加改正，给测量工作带来不便。选择工程控制网局部坐标系统可以有效地将投影长度变形控制在一定的精度范围内，使实测水平边长可以代替高斯平面边长。

地面或轨道面上长度归算至高斯平面后引起的长度综合变形为

取 S=s，R=RA=6 371 km，y、H 以 km 为单位，将上式写成相对变形的形式

令δ=0，则得地面长度归算至高斯平面长度综合变形为零时的测距边高程与横坐标y之间的关系式

如果轨道面高程H与y坐标满足式(3)，则轨道面上所测水平边长无须加改正就可以作为高斯投影面上的边长。按照城市轨道交通工程测量规范的要求，轨道交通工程平面控制网的坐标应与所在城市现有坐标系统一致;轨道工程投影面高程与城市现有坐标系统投影面高程一致，若轨道面平均高程与城市投影面高程的高差影响大于5 mm/km时，应采用其线路轨道平均高程作为投影面高程。因此，选择线路规定平均高程作为投影面后，测距边长改正应小于按式(2)计算的相对误差

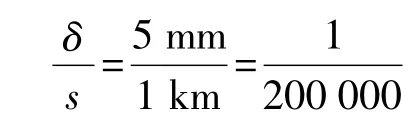
在徐州市轨道交通工程建设中，城市现有坐标系统为1954北京坐标系，城市控制测量投影面(1954椭球面)高程为0 m。地面平均高程为86 m(包括海拔高为36 m，高程异常为50 m)，设计轨道面高程为地下十几米，如取16 m，则轨道面高程为H=70 m，测区平均y坐标为18 km，代入式(2)可得

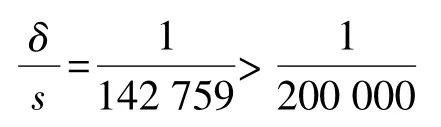
从上述情况来看，如果仍采用城市现有坐标系统，城市控制测量投影面为54椭球面，则长度投影变形不能满足规范规定的要求，应采用其轨道线路平均高程作为投影面高程。

三、城市轨道交通控制测量投影面的选择分析

根据城市轨道交通线路测区的地面高程、设计的轨道面高程和测区高斯平面横坐标y值，选取新的投影椭球面进行高斯投影，得到新的投影平面，使轨道平面上所测平面边长无须加投影改正就可作为新的投影平面上的边长。

以徐州市轨道交通工程为例，轨道工程测区西边坐标 Y1=7.585 km，东边坐标 Y2=28.282 km，测区平均y坐标为18 km。

如图1所示，轨道面高程为Hg=70 m，用测区平均y坐标计算时，上述计算表明，轨道面上的边长归算到原1954椭球面上长度变形大于1/20万。如果用 Y1=7.585 km、Y2=28.282 km 分别代入式(3)，计算长度变形为 δ=0时的 H值分别为 4.516 m、62.701 m，取其平均值 H=33.6 m，该 H 值即为轨道面至新选椭球面的高程。新选椭球面至原1954椭球面高程则为70－33.6=36.4 m。取整数位为36 m，轨道面至新选椭球面高程取整位为34 m。

这天周恺把车停在家门口的暗处，孟丽提着保温饭盒走了出来，上了公交车，他赶紧驱车跟在后面，见孟丽在市人民医院下了车，她走进医院，进入一个病房后，门又关上了。

按轨道面至新选椭球面高程34 m，将Y1=7.585 km、Y2=28.282 km分别代入式(3)，计算轨道面上的边长归算到新选椭球面上长度变形为

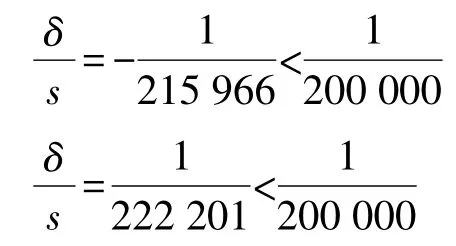
换算为每千米的长度变形分别为－4.6 mm、4.5 mm。

由此可见，对于新选椭球面，在轨道面上进行导线边的测量，归算到新选椭球面上其长度变形满足规范要求的小于5 mm/km，相对变形小于规范要求的小于。

图1 地面、轨道平面、椭球面之间的关系示意图

四、城市轨道交通控制测量坐标系统的建立及其换算的方法

选择新的椭球面后，要建立新的投影平面，建立新的平面坐标系统，以便将1954北京坐标归算到新的投影平面。下面阐述两种方法:一是首先确定新的椭球面相应参数，然后按高斯投影建立新的平面坐标系;二是利用原椭球参数直接按新的投影面高程将原投影面坐标变换到新的投影面坐标。

1.新选椭球面参数的确定

新选椭球面与原1954椭球面“相似”，长半径a、短半径b不同，但其扁率f及偏心率e不变。原椭球面上控制点的大地坐标转换到新的椭球面上，其大地经度不变，但大地纬度改变。从文献［1］可获得新的椭球参数的确定以及控制点的大地纬度变化量的计算方法。

设测区平均纬度为Bm，对应的椭球测区平均半径为Rm，新选椭球面至原椭球面高程为H，对应新选椭球测区平均半径为Rx，新选椭球长、短半径分别为ax、bx。据文献［1］可获得下列公式

2.用原椭球参数计算控制点大地纬度的变化量及其新的大地纬度

控制点的大地坐标在原1954椭球上为(L，B)，在新选椭球上为(Lx，Bx)，据文献［1］可获得下列公式

3.新的投影面坐标转换为实用坐标

新的投影面坐标与原1954椭球面投影坐标相差较大。由于原有地形图坐标是按原1954椭球面投影坐标，这样给实际应用带来许多不便，因此有必要将新选椭球面投影坐标转换为实用坐标。

本文探讨如下两种平面坐标转换方法。

(1)坐标平移法

将各控制点分别计算新椭球面高斯投影坐标与原1954椭球面高斯投影坐标之差，取平均值作为坐标平移参数进行坐标转换。

(2)应用坐标变换公式直接计算实用坐标

从文献［1］可直接按新的投影面高程将原投影面坐标变换为新的投影面坐标。设原投影面坐标为(x，y)，新投影面坐标为(Xx，Yx)，则

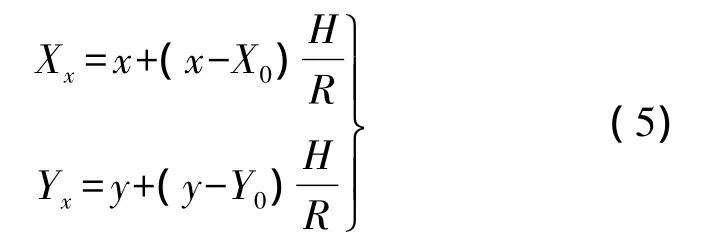
式中，X0、Y0为选择为“原点”的测区内任意一点的平面坐标(或取测区内各控制点的坐标平均值);R为测区平均半径;H为测距边平均高程。

五、工程实例数据分析

按照原1954椭球面长半径a=6 378 245 m、扁率f=1/298.3、短半径 b=6 356 863.019 m、偏心率e2=0.006 693 421 623，e'2=0.006 738 525 4147，新选椭球面大地高H=36 m，测区平均纬度Bm=34°16'，代入上述新选椭球面参数的确定中所列的公式，可计算出新选椭球参数

按式(4)计算各控制点大地纬度改正数dB1=0.003 646″、dB2=0.003 648″、dB3=0.003 649″、dB4=0.003 646″。由于测区范围较小，各控制点大地纬度改正数之差小于0.000 003″，各控制点大地纬度Bx=B+dB。

按新的椭球参数进行高斯投影，计算各控制点的高斯平面坐标见表1。

表1 4个控制点的计算结果表 m

由表1可以看出，新的投影面坐标与原1954椭球面投影坐标相差较大。由于原有地形图坐标是按原1954椭球面投影的坐标，不能满足实际工程的要求，因此需要将新选椭球面投影坐标转换为实用坐标。

表1中4个控制点的坐标差的平均值分别为21.549 6 m 和 0.104 0 m。以此为平移参数，按照坐标平移法将新选椭球面投影坐标转换为实用坐标，具体数据见表2。

表1中将4个控制点的新选投影面平面坐标取平均值(3 273.956 3，18 424.378 7)作为原点(X0，Y0)，H取36 m，R取6 370 380 m，按式(5)将原投影面坐标变换为新的投影面实用坐标，具体数据见表2。

表2 新的投影面坐标转换为实用坐标两种计算方法结果比较 m

由表2可以看出，按坐标平移法转换为实用坐标与按坐标变换公式转换为实用坐标是一致的，其差小于0.000 3 m。但是按坐标变换公式直接转换为实用坐标的计算过程要比按坐标平移法转换为实用坐标简单得多，无须经过计算新选椭球面坐标，直接将原椭球面投影坐标转换为实用坐标。而转换为实用坐标与原1954椭球面投影坐标很接近，这样为使用原有地形图等资料带来了方便。

六、结束语

按照城市轨道交通工程测量规范要求，若轨道面平均高程与城市投影面高程的高差影响大于5 mm/km时，应采用其线路轨道的平均高程作为投影面高程。本文结合徐州城市轨道交通工程平面控制网测量的实际工作，对城市轨道交通控制测量坐标系统的投影面的选择、建立及换算的方法进行了研究和应用，从中得出以下两点体会和建议:

1)在做该类工程项目时，首先要根据轨道面的高程，顾及地面或轨道面上长度归算至高斯平面后引起的长度综合变形，确定新选椭球面的高程H，计算新选椭球参数，取得新选椭球面高斯投影平面坐标。这样在轨道面上进行工程测量时所测平面边长无须加投影改正即认为是新选投影面上的边长。

2)新选投影面坐标往往与原城市投影面坐标相差较大，对在城市轨道交通工程中使用原城市现有地形图、管线图等带来不便，尚需进一步将新选投影面平面坐标通过坐标平移方法或用坐标变换公式直接计算的方法转换为轨道工程测量实用平面坐标。

［1］董鸿闻，李国智，陈士银，等.地理空间定位基准及其应用［M］.北京:测绘出版社，2004.

［2］中华人民共和国建设部，中华人民共和国质量监督检验检疫总局.GB 50308—2008城市轨道交通工程测量规范［S］.北京:中国建筑工业出版社，2008.

［3］张华海，王宝山，赵长胜，等.应用大地测量学［M］.徐州:中国矿业大学出版社，2011.

［4］秦长利.城市轨道交通工程测量［M］.北京:中国建筑工业出版社，2008.

［5］马全明.城市轨道交通工程精密施工测量技术的应用与研究［J］.测绘通报，2010(11):41-45.