跳马落地速度与角度对落地稳定性影响的仿真研究
吴成亮,向家俊,徐 波,李旭鸿,肖晓飞,刘建宇,刘 铮,史东林
体操是我国的优势项目,但从伦敦奥运会和近几届世锦赛成绩来看,这个优势在逐渐缩小,与世界强队的差距正在扩大。体操落地技术是影响比赛成绩的关键因素,它不同于其他项目(如跳高、跳远)的落地动作,它要求落地站稳不动。国际体联会(FIG)在2009年体操落地的评分规则[1]中规定:落地时脚移动一步将导致0.1~0.5的扣分;落地摔倒直接扣1分,而且还存在难度分认定不全风险。在当今的重大国际比赛中,运动员落地能否站稳不动,已成为能否夺冠和取得好成绩的决定性因素之一。跳马落地难度较大,也具有典型性;因此,研究跳马落地稳定性是体育科学工作者们关注的热点问题,并受到广大教练员和运动员的重视。跳马一般由8个动作阶段组成,包括助跑、趋步、踺子、踺子踏跳、第一腾空、推马、第二腾空和落地[2]。如今跳马不断地朝多轴的复合翻转方向发展,这无疑加大了落地稳定性的难度。黄强等[3]对27届奥运会我国男子体操选手落地稳定性进行统计与分析,结果表明落地动作完成较差,落地稳定的仅占43.19%。北京奥运会女子跳马落地稳定性也不乐观,在决赛16次试跳中,无一人能站稳,大部分选手落地会有一小步或中步移动,有4名运动员落地失败。可见,跳马落地稳定与否成为制约跳马成绩的关键因素。
目前,对跳马落地稳定性影响的研究主要集中在跳马落地技术与落地方式、肌肉组织的刚度和力量、心理调控能力等。严波涛等[4]对30人次的跳马落地进行分析,建立跳马落地的运动方程,指出落地的稳定性需要高质量的空中动作,旋翻转体周数尽量提前完成,留有充足的空间和时间展体收臂准备着地。姚吉庆[5]对体操跳马落地技术稳定性中分析指出:第2腾空阶段技术好坏直接影响着落地技术的稳定性;良好的空间、时间知觉和训练比赛中情绪变化也会影响到落地技术的稳定性。现有大多数研究是运用生物力学原理对落地稳定性进行定性分析,鲜有实验数据作为支撑,且推理过程往往较为繁琐;所以,本文在不考虑其他因素的前提下,旨在通过计算机建模与仿真技术,从速度和角度2个方面来分析跳马落地的稳定性。
1 研究对象与方法
1.1 研究对象
程某,中国体操跳马前世界冠军,1988年出生,身高1.52 m,体重41kg。
洪某,朝鲜体操跳马前奥运冠军,1986年出生,身高1.54 m,体重42kg。
1.2 研究方法
1.2.1 三维运动学分析
对程某和洪某完成的“踺子转体180°前手翻接直体前空翻转体180°”跳马动作,进行三维运动学分析。使用Troubleshooter高速摄像机拍摄,2台摄像机同在跑道一侧,夹角约70°,拍摄频率为250帧/s。采用SIMI Motion软件进行解析,获得人体运动轨迹坐标、速度等运动学数据。
1.2.2 计算机仿真技术
基于MSC.ADAMS/LifeMod运动仿真软件,输入受试对象的性别、年龄、身高和体重等人体形态参数,根据人体模型数据库GEBOD(Generator of Body Data)中的回归方程计算得到环节长度、围度和人体惯性参数等,建立19环节的人体模型,各环节之间由不同自由度的铰链连接,共有52个自由度[6]。在此人体模型基础上,对各环节的关节铰链赋予约束,并调整人体模型的初始姿态,使它更接近实际的运动状态;然后进行平衡分析,即将运动学解析得到的2人跳马动作中人体各个关节的三维坐标赋予三维人体模型,其目的是使人体模型的关节中心和实际人体关节运动坐标点相匹配。再按GB/T 23124—2008建立跳马的落地环境,即与人体相接触的体操落地垫,并完成与人体模型的接触。通过逆向动力学分析,记录人体运动轨迹和各个关节力及力矩,再进行正向动力学分析,在关节力及力矩的驱动下,实现跳马运动员落地过程中的人体运动仿真。最后将人在推离马瞬间,身体重心的水平速度(vx)和垂直速度(vz)作为输入条件变量,改变该变量值,以100%、105%及110%人体重心vx和vz组合输入,进行仿真实验,如图1所示。
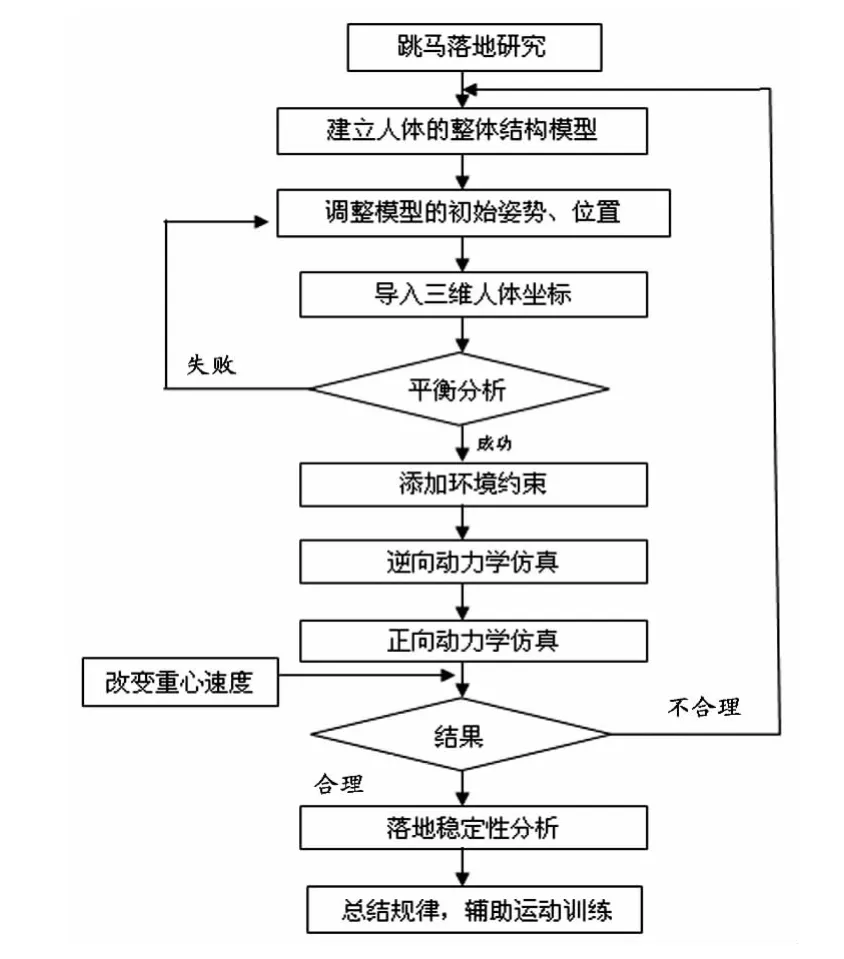
图1 跳马落地建模与仿真实验流程
计算机仿真软件MSC.ADAMS/LifeMod基于带乘子的拉格朗日方程,并根据人体模型最终建立如下方程[8]:
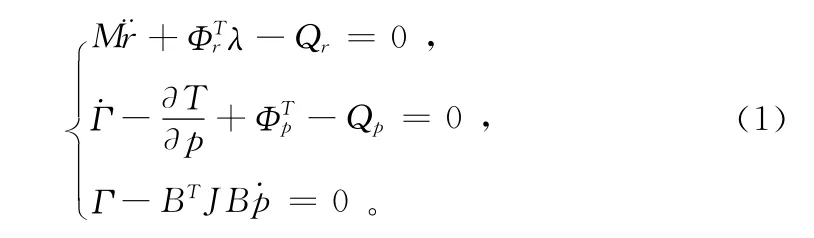
其中:M为广义质量矩阵;Q为广义外力矩阵;r、p为广义位移矩阵;Γ为广义角动量矩阵。最后需要输出的仿真实验结果是:落地瞬间人体的姿态角和人体重心的水平速度,如图2所示。
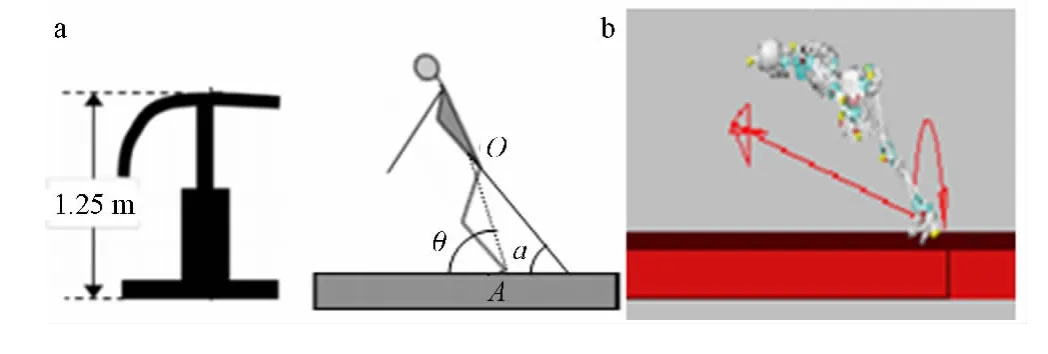
图2 跳马落地示意(a)和跳马落地动作的计算机仿真(b)
2 结果
表1为在推离马时将人体重心的水平速度vx和垂直速度vz作为变量输入仿真模型,通过计算机仿真实验后,得到落地瞬间人体的姿态角和人体重心的水平速度。从表1可以看出,当只增加推离马的水平速度vx时,落地时的水平速度也相应增加,但是人体落地姿态角是先增加后下降的。当只增加推离马的垂直速度vz时,落地时的水平速度没有增加,人体落地姿态角变化暂不显示规律性。当推离马的水平速度vx和垂直速度vz同时增加时,落地时的水平速度和人体落地姿态角都相应增加了。
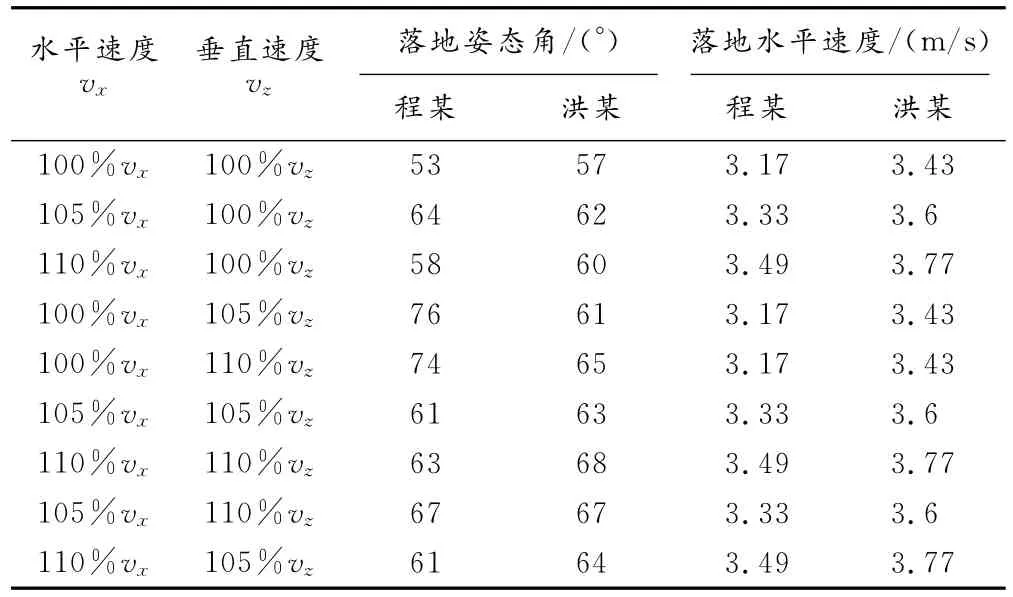
表1 程某、洪某在推离马时不同水平速度和垂直速度下,落地瞬间身体姿态角和水平速度
如图3所示,仅改变程某推离马时身体重心垂直速度,左图的实线表示该动作的实际速度(2.64m/s,高速摄影解析得到的速度在这里称为实际速度),虚线“--”表示105%实际速度(2.80m/s),隔 点 虚 线 “-·-”表 示 110% 的 实 际 速 度 (2.94 m/s)。右图黑色方块和斜线方块分别代表在这3种重心垂直速度下第2腾空所用时间和人体重心水平位移,3条曲线可以明显地看到程某第2腾空阶段盆骨中心的高度随时间的变化情况,身体重心垂直速度越大,人体盆骨中心越高;从柱形图来看,身体重心垂直速度的增加,也带来人体的水平位移和第2腾空所用时间的增加。

图3 程某推离马时重心不同垂直速度,人体盆骨中心高度-时间变化曲线(左),身体水平位移及第二腾空时间(右)
如图4所示,仅改变程某推离马时身体重心水平速度,左图实线表示该动作的实际速度(3.17m/s),虚线表示105%的实际速度(3.33m/s)。右图黑色方块和斜线方块分别代表在这2种重心水平速度下第2腾空所用时间和人体重心水平位移。从曲线图可以看到,2条实线和虚线完全重合,看起来只有1条曲线;所以,身体重心水平速度的改变,对于骨盆中心高度没有变化。从柱形图上看,当身体重心水平速度增加了,人体的水平位移也会增加,但第2腾空所用时间没有增加。图5为程某(左)和洪某(右)跳马第2腾空及落地动作仿真图。
据统计,2013年,湖南累计投入抗旱资金24.2亿元,抗旱机电井25.5万眼、抗旱泵站3.86万处、机动抗旱设备83.8万套、运水车辆1.75万辆,完成抗旱灌溉面积1958万亩,挽回粮食损失300多万t,减少经济作物损失60亿元,临时解决了314万人的饮水困难,有效保障了群众生活和农业生产安全。
3 分析与讨论
体操技术发展迅速,跳马空中动作越来越惊险、复杂,它既要表现出“高飘”,又要表现出舒展大方,最后落地要稳定,给人以美的享受。跳马落地瞬间,通常是决定成败的关键。随着跳马难度增加,落地的稳定性相对下降,如果不注意落地中的技术问题,还容易造成关节损伤,尤其是膝、踝关节[9]。人体运动的计算机仿真是运动生物力学理论方法中较高层次的研究内容[10],它可以实现人体运动的计算机仿真实验及结果的可视化[11],为揭示运动技术特点提供直观的素材,为教练员指导跳马训练提供科学的理论依据。
3.1 跳马落地技术分析
落地技术是指跳马动作技术环节中,从脚接触体操落地垫,再经过缓冲到身体起立站稳阶段的技术[12]。落地技术稳定性实际上是指运动员根据不同的下法动作充分调整身体姿势,抵消倾倒力矩能力的稳定性。落地技术它包括相互联系的2个阶段:准备阶段、落地缓冲阶段。
准备阶段中,人体在空中完成各种动作难度后,两脚在还未触垫前,身体处于准备落地姿态。这一阶段对落地的稳定性有直接影响,跳马第2腾空动作一般以绕人体横轴较多。根据转动惯量原理:I=mR2(其中m为人体的质量,R为人体的回转半径)。m不变,I与R2成正比,即R增大到原来的2倍,I就增大到原来的4倍。此外,I与角速度ω成反比(人在腾空之后,只受重力作用,根据动量矩守恒:Iω=常量),所以当R增大时,I随增大,而ω减小,即当人体转动的半径增大时,其转动速度相应减小。因此,在人体完成空翻动作后,身体要做一定的伸展,以减小落地时的角速度,增加落地的稳定性。另外,这样做同时增加肌肉的初长度,使落地时肌肉发挥更大的力量,有助于落地站稳。

图4 程某推离马时重心不同水平速度,人体盆骨中心高度-时间变化曲线(左),身体水平位移及第二腾空时间(右)
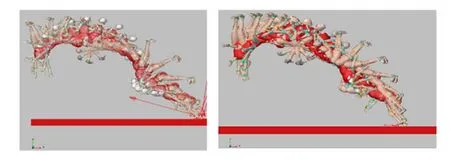
图5 程某(左),洪某(右)跳马第二腾空及落地仿真
落地缓冲阶段,此阶段又包括一个较短的冲击阶段和一个较长的平衡稳定阶段[13]。在冲击阶段,脚-落地垫间存在较大的地面反作用力(GRF),其峰值随着推离马高度(第2腾空高度)增加而增大,大约是运动员自身体重的8~14倍,而在较长的平衡稳定阶段,GRF大致为其体重[14]。落地缓冲技术是稳定的关键,其生物力学特点是落地瞬间的水平分力及翻转力矩,通过合理缓冲使之消失,垂直分力逐渐趋近体重,即人体所受的合外力、合外力矩为零。在缓冲制动过程中,动力矩M主动必须始终大于破坏平衡的倾倒力矩M倾倒。当制动结束时M主动=M倾倒,此时人体站立不动;所以人体受到的合外力、合外力矩为零,是站稳不动的必要和充分的条件。冲击阶段双腿肌肉用力特点是由积极主动的退让性工作过渡到克制性工作;落地方式由脚尖落地过渡到全脚掌,原因在于足尖落地时足弓等部位较好的变形和缓冲、踝关节处肌肉的预激活等大大降低了脚跟的负荷。双臂需要适度摆动,以保持平衡。
3.2 跳马计算机仿真模型的落地速度及角度分析
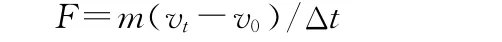
其中F为冲力(即地面给人体作用力的合力),m为人体质量,vt为瞬时末速度,v0为瞬时初速度,Δt为人体接触地面缓冲时间。人体质量m一般短时间内不会改变,人体接触地面缓冲时间Δt越长,F会越小,落地会越稳定;但Δt与落地高度、动作控制、下肢神经肌内的控制和协调能力、肌肉组织的刚度和力量、落地方式和落地垫的力学特性等因素都有关[18],相互关系较为复杂,不做详细讨论。本文假定Δt不变,只探讨落地的速度和角度对跳马落地稳定性的影响。落地瞬时末速度vt一般为零,所以当落地瞬时初速度v0越大时,F越大,人要落地站稳越难。落地垂直速度是由落地高度决定的,落地高度越高,第2腾空的时间越长,运动员有足够的时间完成翻腾和/或转体动作,这就越有利于跳马动作的完成;所以不应该以牺牲落地垂直速度为代价,影响落地高度。因此,减小落地时的水平速度,是增加落地稳定性的很好选择,但是过小的水平速度,可能引起落地阶段的远度不足,造成完成分(E分)被扣[1]。所以,在跳马的计算机仿真实验中,为了不影响落地稳定性,在不减小落地水平速度的情况下,应增加推离马的垂直速度,来增加第2腾空高度,这有利于跳马动作的完成。
本研究通过计算机仿真实验,只增加推离马的垂直速度,对于落地姿态角影响不大,在53°~76°内呈不规则变化(见表1)。只增加推离马的水平速度时,落地姿态角先增加后减小,姿态角的减小是为了降低水平速度的增加对落地稳定性的影响。设人体落地时主矢和主矩不为零,主矢量与地面有夹角为α(如图2所示),则相对A点产生动量矩MA,其大小MA=mvrsin(θ-α)(顺时针方向),其中v为O点瞬间线速度(以A为支点,OA为半径r的转动);重力相对A点产生重力矩M重=mgrcosθ(逆时针方向)。当MA=M重,人体落地站立不动,这是理想结果。当MA>M重或MA<M重时,则人体前倒或后倒。

若MA=M重,即mvrsin(θ-α)=mgrcosθ,那么 在不考虑跳马落地失败的情况下,由表1可知,人体落地姿态角θ范围在53°~76°,为锐角,又因为α≤θ,则
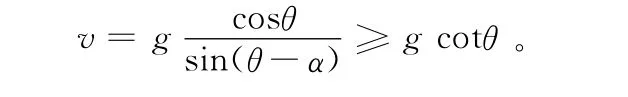
假设当角α=0,即v正好等于人体落地水平速度,则
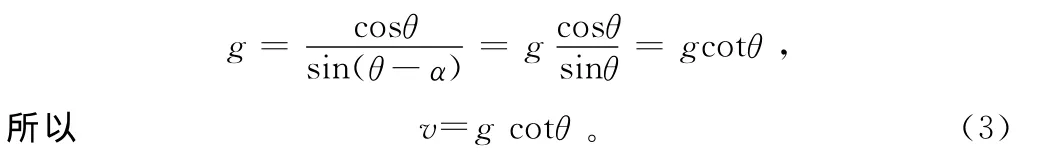
假设当α=90°,v为人体落地垂直速度,此时落地无水平速度,落地的稳定性更多与人体落地缓冲能力有关。
通常情况下,运动员跳马落地是既有水平速度又有垂直速度。人体垂直速度给落地带来的不稳定因素更多与运动员的缓冲能力有关,本文不做讨论。而对于跳马中人体落地水平速度与落地姿态角应更多地考虑v=gcotθ的函数关系,通过计算机仿真获知,人体落地姿态角θ范围在53°~76°,函数在该区间为减函数;所以,人体水平速度与落地姿态角应该呈负相关,即当水平速度增加时,落地姿态角必须减小才能满足落地的稳定性。但是落地姿态角减少,将使人在落地时控制平衡的难度增大,使落地稳定的风险增加。当推离马的水平速度和垂直速度同时增加时,落地姿态角和水平速度都会增加,MA将进一步增加,人体向后倾倒趋势增加,造成落地稳定的难度更大。
本文还对计算机仿真实验结果,进行了理论验证。根据抛物线运动原理,跳马第2腾空到落地过程,属于落地点在抛出点下的抛物线运动。设v0为推离马瞬间身体重心速度,φ为v0与水平夹角,则有,推离马瞬间身体重心水平速度vx=v0cosφ,垂直速度vz=v0sinφ。
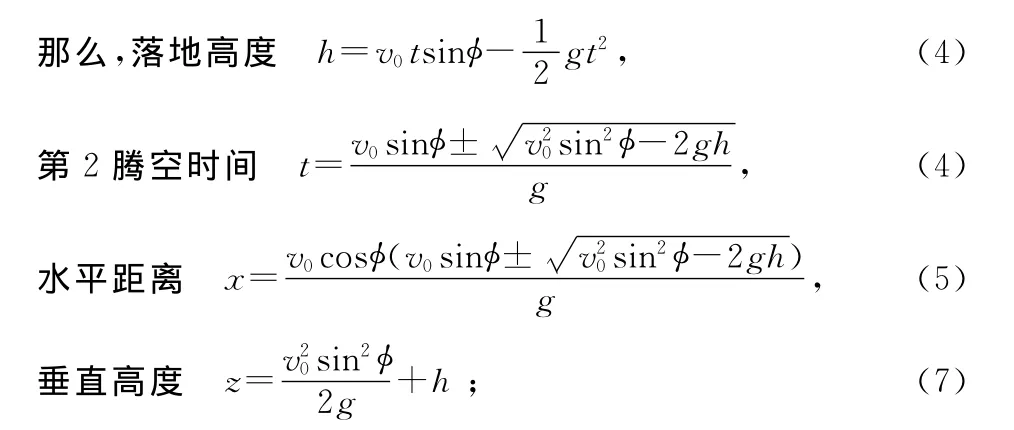
所以,式(5)和(6)式分别说明在抛物线运动中,物体飞行时间和高度由初速度的垂直分量决定,而不受初速度水平分量的影响(不计空气阻力)。如图3所示,身体重心的垂直速度增加了,第2腾空高度和所用时间都会增加,有更多的时间和空间完成第2腾空动作,提高伸展身体,增加落地的稳定性。而在图4中,只改变了身体重心的水平速度,垂直速度没有改变,所以第2腾空高度和所用时间都没有发生改变,而落地的水平距离增加,这样就增加了落地稳定的难度。以上采用计算机仿真实验所得出的仿真结果,与抛物线运动原理相吻合,这就从抛物线运动原理对本研究中计算机仿真实验结果进行了理论验证。
4 结论
本文利用高速摄影这一运动生物力学较为成熟的技术手段,获得人体运动三维坐标,再基于MSC.ADAMS/LifeMod多体动力学仿真软件,对跳马落地进行仿真实验。以跳马推离马时的水平速度和垂直速度作为变量,获得不同条件下的落地水平速度和落地姿态角,并分析它们对落地稳定性的影响。结果表明:在跳马落地的最佳策略为,在保持推离马时人体重心水平速度不减小的情况下,增加其垂直速度,能产生更多的时间和空间完成第2腾空动作,并为落地作积极准备;而在即将落地前,身体要做一定的伸展,以减小落地时的角速度,增大落地时的转动惯量,从而增加落地的稳定性。
诚然,本研究仅从落地速度和角度来评判落地稳定性,不可避免地存在一些局限性。本文将人体简化为多刚体模型,忽略了肌肉和软组织对运动的影响,本身会带来一定误差。尽管如此,但我们可以通过模型评估出很难在人体上测量的结果,从而确定最佳的运动模式。今后的研究方向需要将模型的效度不断提高,将肌肉和软组织引入。综上所述,计算机仿真技术也必将在运动训练指导及运动损伤预防上拥有广泛的应用前景。
[1]国际体操联合会.女子竞技体操评分规则[S].2006.
[2]郝卫亚,姚侠文,庞乐.程菲跳运动学分析[J].中国体育科技,2007,43(6):76-79.
[3]黄强,蒋小娟.对第27届悉尼奥运会我国男子体操选手落地稳定性的统计与分析[J].福建体育科技,2001,20(3):16-19.
[4]严波涛,于长菊,张伯强.体操跳跃类动作落地稳定性的生物力学原理探讨[J].西安体育学院学报,1994.11(2):64-71.
[5]姚吉庆.论竞技体操跳马落地技术稳定性[J].武汉体育学院学报,2003,37(3):74-76.
[6]吴成亮,郝卫亚.跳马过程中人-器械动力学关系的研究[J].中国体育科技,2011,47(6):25-29.
[7]GB/T23124-2008.中华人民共和国国家标准跳跃平台[S].2008.
[8]刘雷.人体运动仿真建模方法研究[J].计算机仿真,2009(1):166-168.
[9]弗拉基米尔M·扎齐奥尔斯基.运动生物力学[M].北京:人民体育出版社,2004:531-554.
[10]卢德明.运动生物力学测试方法[M].北京:北京体育大学出版社,2001:222-226.
[11]郝卫亚.人体运动的生物力学建模与计算机仿真进展[J].医用生物力学,2011,26(4):97-103.
[12]李旭鸿,郝卫亚.落地冲击引起下肢损伤的生物力学研究进展[J].中国运动医学杂志,2013,32(2):186-189.
[13]McNitt-Gray J L.Kinematics and impulse characteristics of drop landings from three heights[J].Int J Sport Biomech,1991,7(9):201-224.
[14]McNitt-Gray J L,Hester D M E,Mathiyakom W,et al.Mechanical demand and multijoint control during danding depend on orientation of the body segments relative to the reaction force[J].J Biomech,2001,34(11):1471-1482.

