基于SWAN模式的全球有效波高数值预报结果之初步验证

梁小力，王 毅

(1.国家海洋环境预报中心，北京100081；2.国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室，北京100081）

基于SWAN模式的全球有效波高数值预报结果之初步验证

梁小力1,2，王 毅1,2

(1.国家海洋环境预报中心，北京100081；2.国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室，北京100081）

利用国家海洋环境预报中心基于SWAN模式和NCEP预报风场模拟的全球海浪预报场，结合Jason-2卫星高度计和NDBC浮标资料对全球海浪场进行了自2013年7月到2014年6月为期1 a的统计检验。结果表明：预报波高与实测值吻合较好,24 h、48 h、72 h预报的均方根误差均小于0.6m，偏差绝对值均小于0.1m，相关系数均大于0.91。有效波高的预报精度随预报时效的增加而降低，预报误差在48 h内变化不大，而在48 h后明显增大。有效波高的预报偏差存在地域性差别，全球西风带和热带地区的偏差较大，而赤道无风带和副热带高压控制地区的偏差较小。

SWAN模式；海浪预报；有效波高；统计检验

1引言

数值模式预报是海浪预报的重要发展方向，目前国内外海洋预报部门已广泛应用第3代海浪模式开展了业务化预报。如欧洲中期天气预报中心（ECMWF）把最早的第三代海浪模式WAM与大气、海洋模式耦合起来，建立了全球和区域海浪预报系统[1]。美国国家环境预报中心（NOAA/NCEP）研发了NWW 3（NoaaWaveWatch III）模式，并以此为基础建立了包括全球、三大洋、多个重点区域的双向嵌套海浪预报系统[2-5]。美国海军舰队数值气象和海洋中心(FNMOC)利用WW 3模式建立了全球和区域尺度的海浪预报系统[6]。日本利用自主发展的MRI模式开展了全球和区域海浪预报[7]。韩国、澳大利亚和法国等国家利用WAM和WW 3模式建立了全球海浪预报系统[8]。我国国家海洋环境预报中心（NMEFC）以WAM、WW 3和SWAN（Simulating Waves Near shore）模式为基础，先后建立了西北太平洋、中国近海和全球海浪预报系统。

SWAN模式最初是用于计算近岸浅水区海浪的数值模式，近20 a经过不断地改进和扩充，考虑了许多物理过程和当今最新海浪研究成果，性能不断提高并成为适用于任何尺度的海浪数值模式[9-10]。从2005年开始，国家海洋环境预报中心对SWAN模式进行技术改进并应用于全球海浪业务化数值预报。本文利用同期的Jason-2卫星高度计和NDBC浮标资料对该预报系统进行了检验分析,从多方面考察了该预报系统的预报效果，为进一步提高全球海浪业务化预报能力提供参考。

2模式和数据

2.1 SWAN模式介绍

SWAN是由荷兰Delft科技大学开发的第3代海浪数值模式。SWAN模式采用了基于Euler近似的作用量平衡方程和线性随机表面重力波理论，计算时可考虑波浪风输入、波浪浅化、逆流阻碍和反射、折射、白帽破碎、水底摩擦、三波和四波非线性

相互作用等物理过程。在SWAN海浪模式中，用二维波作用量N(σ,θ)来描述随机波浪场，作用量的变化率可以用作用量平衡方程表示为[11]:

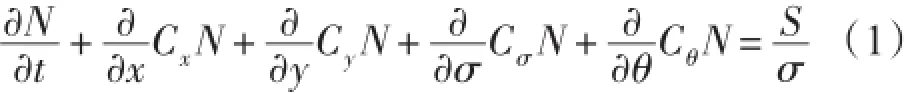
式中：左边第1项代表作用量随时间的变化率；第2项至第5项代表作用量在几何和物理空间中传播；方程右边的S代表能量源汇项，包括风能输入、波波非线性相互作用和由底摩擦、白冠、破碎等引起的能量损耗。

截至目前,在第3代海浪模式深水物理过程的研究中，关于风能量输入和非线性波—波相互作用等物理过程的研究远比海浪耗散更充分，因此在第3代模式中通常把海浪耗散作为一个最不确定的物理过程加以调整和改进[12-14]。本文模式的耗散过程采用Wang等[15]提出的改进饱和型风浪耗散方案，该方案在Banner等[16]和Westhuysen等[17]的基础上，根据海浪谱的观测研究把高频Phillips饱和参数看作随波龄变化，并由观测分析直接得到其变化规律[18-19]。低频部分则在传统的白冠破碎的基础上，引进了反波龄参数来调整海浪耗散率，并把海浪耗散系数与频率之间的依赖关系调试为σ3（σ为角频率）。对于高低频耗散衔接方式，采取了类似于NWW 3模式的处理方法，即高频耗散和低频耗散以两倍峰频率2σp为界限，在σ＜2σp时采用公式（2）：

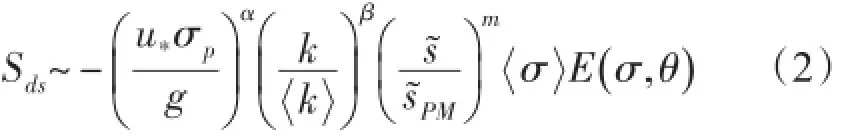
而σ＞2σp时增加了饱和门限项，两部分以一个光滑函数fbr衔接。最终的海浪耗散参数化具体形式如下：

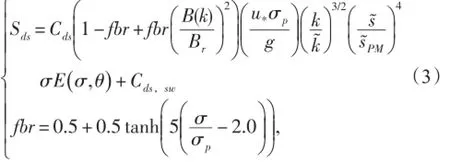
式中：u*为摩擦风速，Cds为可调系数，这里取63.7，σp是风浪峰频率,Cds，sw是经验的涌浪耗散率，此处参考Ardhuin[20]取4.2e-6。

2.2 海浪预报资料

本文利用的海浪预报资料为国家海洋环境预报中心提供的海浪数值业务预报数据。该数据每天预报1次，起报时间为12时（世界时，下同），用到的强迫风场是起报时间为12时分辨率为1°×1°的NCEP海面风场预报。基础地形数据来自于NGDC（NationalGeophysicalData Center）的全球（1/12°）分辨率的TerrainBase数据。计算区域的经纬度范围分别为180°W—180°E和78°S—78°N，空间分辨率为1°×1°，预报时效为85 h。海浪谱的频率范围是0.040—0.394 Hz，按对数平均分为25个频率，海浪谱方向平均分为24个方向。模式的物理过程采用Jassen参数化，海浪耗散参数化如上一节所述，四波相互作用采用DIA近似，差分格式为三阶隐式迎风差[15]。

2.3 卫星资料

用于全球检验的高度计数据为NASA提供的Jason-2卫星高度计有效波高数据。该卫星发射于2008年6月20日，轨道高度为1336 km，轨道倾角为66.039°,重访周期约为10 d，频率为5.3/13.6 GHz。本文选用数据的时间窗口为2013年7月1日至2014年6月30日，空间窗口为55°S—55°N、180°W—180°E。由于卫星高度计在反演大风速下有效波高时的局限性，对大于12m的高度计有效波高作了截断处理。

2.4 浮标资料

本文同时利用美国国家浮标资料中心(NationalData Buoy Center，NDBC)提供的观测资料进行检验。该浮标资料为经质量控制的标准气象数据，时间分辨率为1 h。由于本文研究的是全球海浪预报，因此近岸浮标就不具备代表性。故同时选取了6个非近岸浮标进行比较检验，所选浮标信息和位置分布如表1和图1所示。

2.5 统计检验方法

本文将对预报的有效波高进行统计检验，虽然有效波高是从统计的角度对海况进行描述，但其对于海上和沿海的生产活动都很有意义，因此一般被

认为是最有用的海况参数。为了检验海浪预报的效果，在统计分析过程中把预报时效为0—24 h的所有预报结果作为同一个统计组，同理24—48 h预报、48—72 h预报的含义与此类似。对所有统计组按月进行统计检验,检验统计量包括：偏差、均方根误差、相关系数、相对误差和离散指数，其含义由公式（4）—（8）定义为:

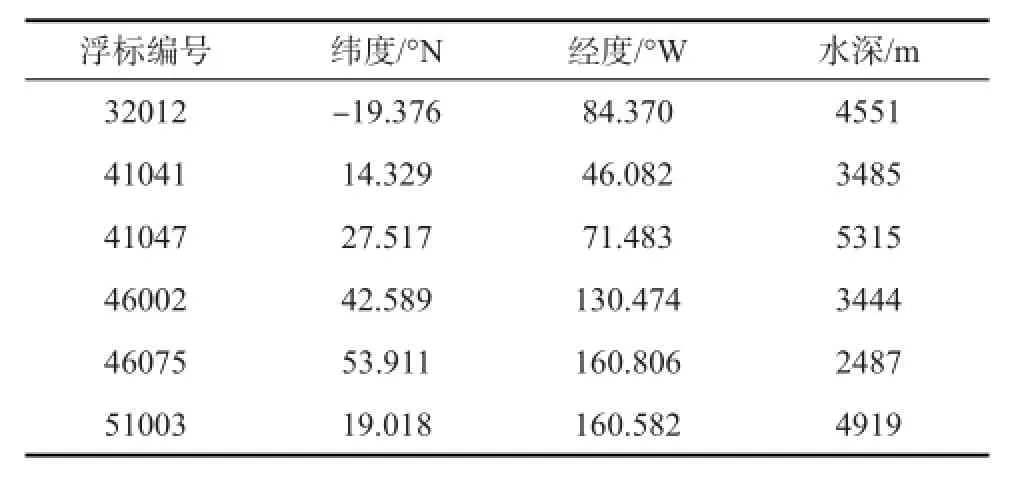
表1 浮标信息表

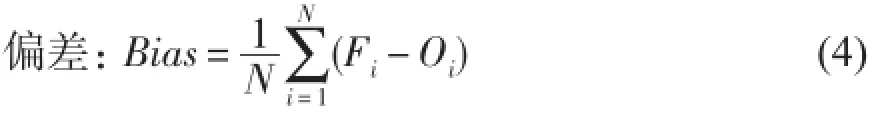
均方根误差:

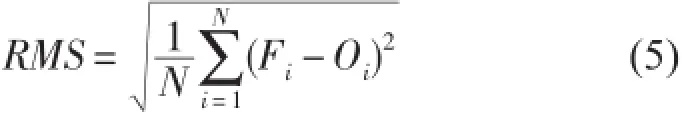
相关系数：

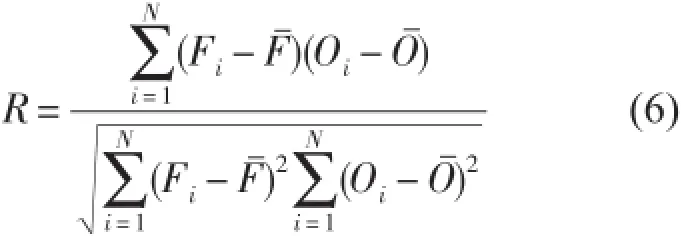
相对误差：

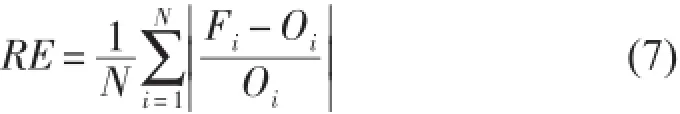
离散指数：

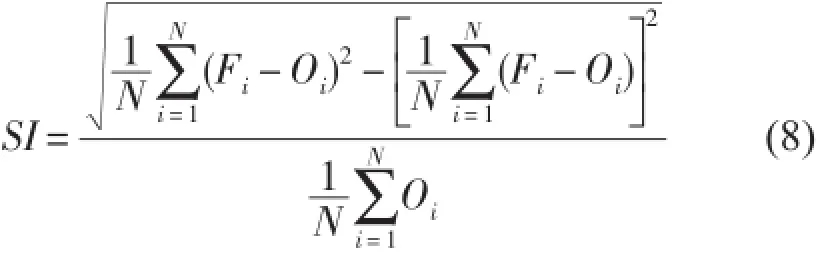
表2 卫星数据统计检验结果

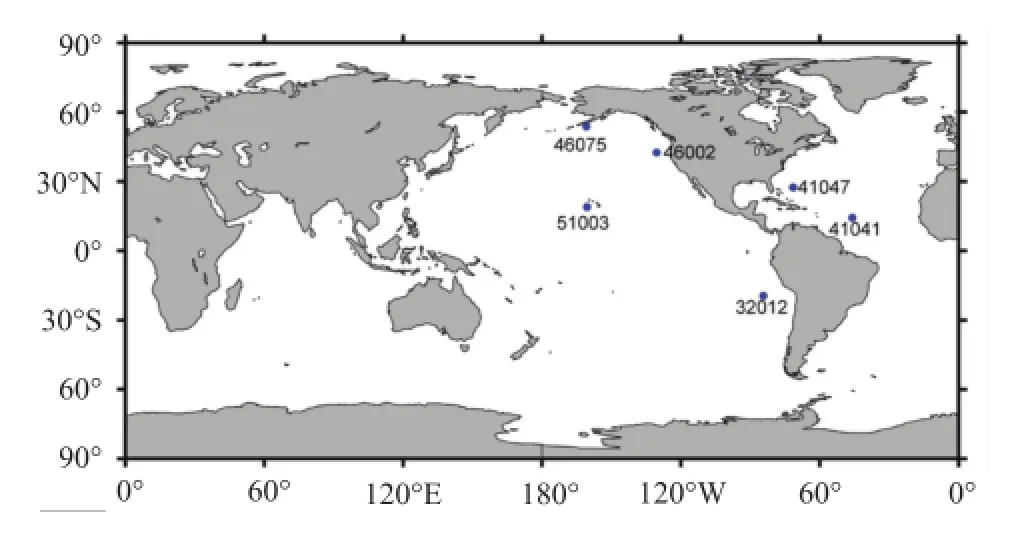
图1 浮标分布图

式中：Oi为观测值；Fi为预报值；Oˉ为观测平均值；ˉ为预报平均值；N为样本数。

3卫星数据检验

3.1 月统计高度计检验

卫星数据具有浮标数据所不具备的空间代表性，为了检验全球海浪预报的效果,利用Jason-2卫星高度计有效波高数据来检验2013年7月至2014年6月为期1年的全球海浪日常预报。在检验过程中，分别对0—24 h、24—48 h、48—72 h预报的统计组结果进行统计量检验，计算其偏差、均方根误差和相关系数的月平均结果，再对所得的统计检验结果进行年平均，所得结果如表2所示。

从卫星数据检验结果（见表2）来看，24 h、48 h、72 h预报均具有较小且相近的正偏差。各统计组的均方根误差、相对误差和离散指数都存在较明显的差异，表现为24 h预报＜48 h预报＜72 h预报，且误差增幅随预报时效逐渐增大，均方根误差（RMS）从6%增大到11%；相对误差（RE）从4%增大到7%；离散指数（SI）从6%增大到11%。有效波高的预报值和观测值呈明显的相关关系，相关系数介于0.91—0.94，以24 h预报为最高，同时相关系数随预报时效增大而减小。为进一步分析各统计量的特征，对各统计组的月平均检验结果进行比较，结果如图2所示。

图2 有效波高月平均统计检验

从图2中可以发现离散指数和相对误差都没有明显的月变化，且随预报时效的增长变化幅度较小。偏差、均方根误差和相关系数则存在月变化且变化趋势比较一致，在夏季和冬季增大，春季和秋季减小。偏差和均方根误差在9月份都较大，同时在3月份也有类似的情况，但不如9月的幅度大，说明预报质量在季节转化期有所下降。另一方面，均方根误差（相关系数）随预报时效的增长而增大（减小），且在0—48 h内变化较小，而在48—72 h内变化较大。

3.2 散点图分析

由于数据量较大，时间序列无法给出卫星验证资料集的直观分析，故分别以卫星观测和模式预报对应点上的有效波高数据作为散点的横纵坐标绘制散点图（见图3a，b，c），虚线为最小二乘拟合直线，并计算卫星观测与预报的有效波高之差得到波高差的频数直方图（图3d，e，f）进行比较。

从有效波高的散点图（图3a，b，c）来看，0—24 h预报和24—48 h预报结果相差不大，而48—72 h预报则明显不同，预报与观测差异较大的个例明显增多。从统计检验量来看，均方根误差和离散指数随预报时效增加而增大，但偏差没有明显变化。从波高差的频数直方图（图3d，e，f）可以发现波高之差主要分布于±0.5m之间，且最大累计频数对应的波高差更偏向于正值；即总的来说模式预报值相对于卫星观测值偏大，偏大程度随预报时效增加而减小。另外，无论是24 h、48 h还是72 h预报，对于浪高较小的波浪，模式预报结果都表现较好。

3.3 纬向平均预报偏差分析

为了解模式在全球的预报质量，求得0—24 h预报结果的全球年平均偏差分布如图4a所示。同时对0—24 h、24—48 h和48—72 h预报统计组中的预报值和观测值分别求纬向平均，并计算预报波高在各纬度的平均偏差得到图4b—d。

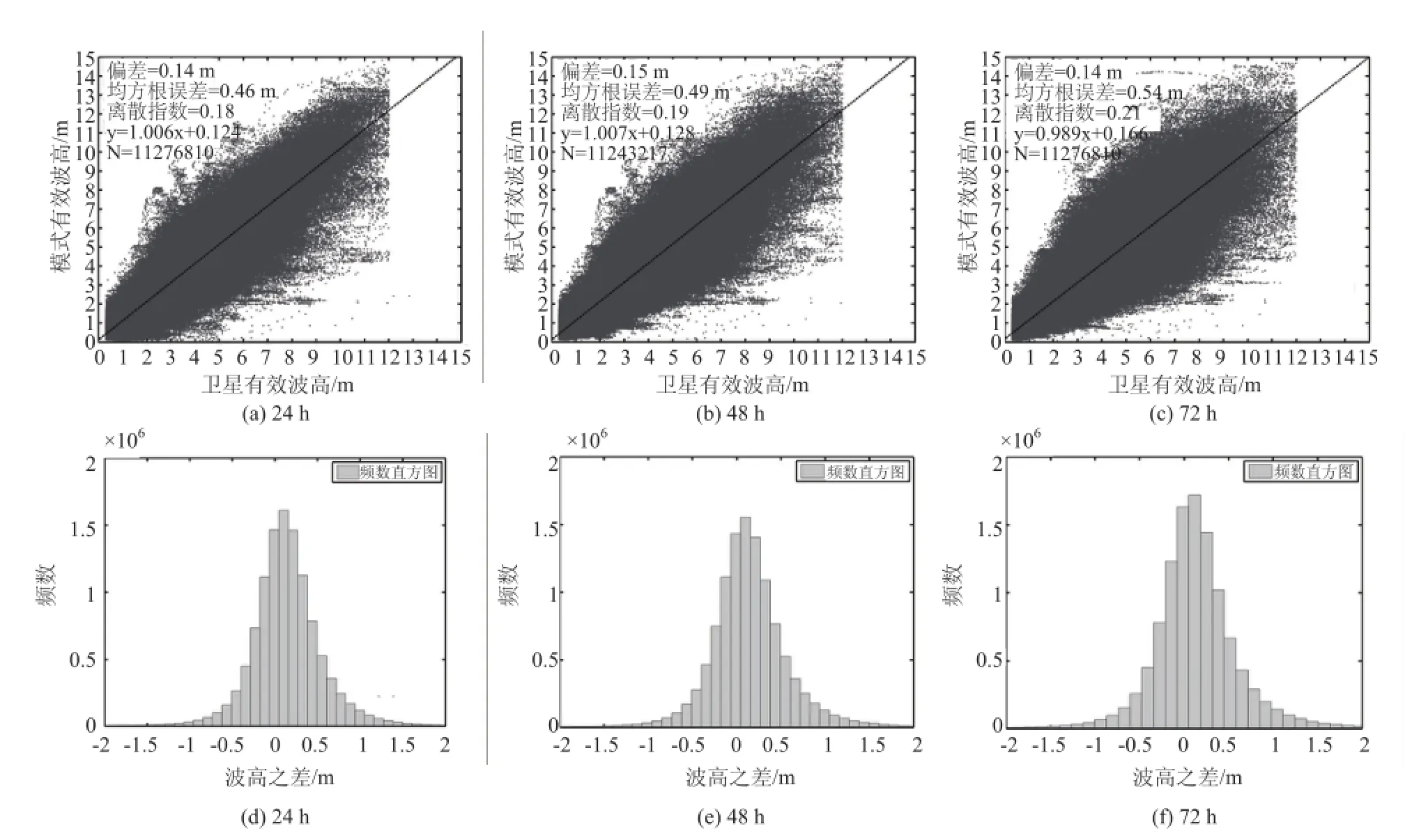
图3 预报与卫星观测对比

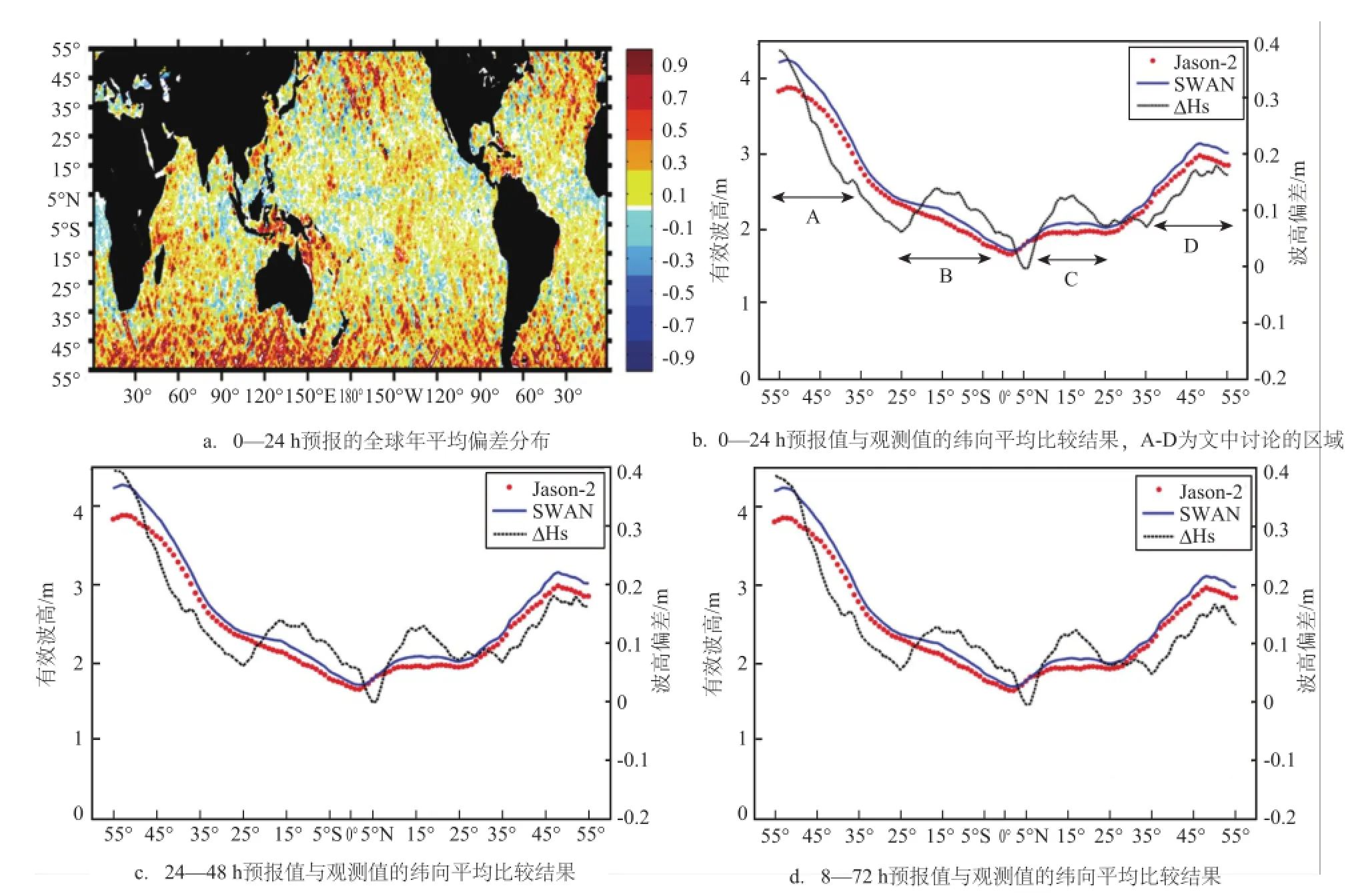
图4 有效波高纬向平均比较

从图4a中可以发现，0—24 h预报的有效波高偏差在全球各纬度存在明显差异。结合纬向平均波高偏差分布结果（见图4b）可以发现，纬向平均波高偏差的总体分布特征为由赤道向两极增大，且在各纬度均为正偏差。其中南半球西风带的纬向平均偏差最大（对应图4b中A区域），北半球西风带次之（对应图4b中D区域），同时南北半球的热带地区各存在一个明显的大值区（对应图4b中B和C区域），而赤道无风带（对应图4b中B与C间的区域）和副热带高压控制区域（分别对应图4b中A、B与C、D间的区域）的纬向平均偏差较小。从图4b—d中还可以发现，各预报时效的纬向平均波高偏差的分布情况基本一致。

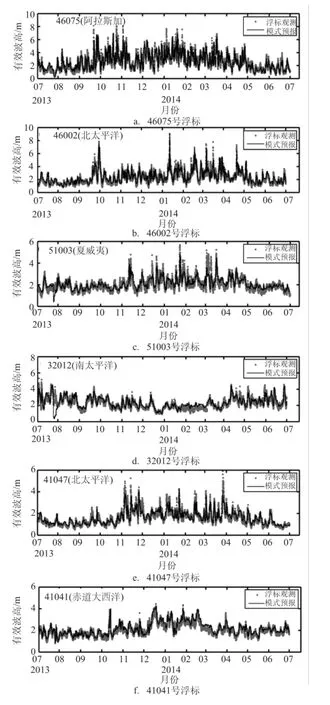
图5 模式预报与浮标观测时间序列比较

4浮标数据检验

4.1 时间序列分析

与卫星高度计数据相比，浮标数据具有很好的时间代表性。为了进一步检验模式在全球各海域的预报质量，选取了6个深海浮标数据进行比较检验。将0—24 h预报结果与同期的浮标资料绘制成时间序列进行比较，所得结果如图5所示。

图5b为北太平洋46002号浮标的一个时间序列，该区域预报结果和观测十分吻合，同时模式对波高的极值和变化趋势均表现出了逼真的模拟能力。图5d为南太平洋32012号浮标的对比，可以发现除了7月底的一小段异常表现和2月的略高估计之外，预报结果还是可以很好地模拟浪高的极值和变化趋势。比较其他浮标结果（46075、51003和41047号浮标）可以发现模式结果在北半球的冬半年虽然可以较好地捕捉到波高的变化，但却未能模拟出许多波高的极端状况，如有效波高在大波高情况下偏小，在小波高情况下偏大。这些极端例子可能是受北半球冬半年风暴作用较强的影响，使得时间尺度（或空间尺度）较小的极端海浪事件无法被恰当的模拟出来。

4.2 月统计浮标检验

与高度计检验类似，将各浮标与预报对应的有效波高数据按预报时效分为3个统计组分别进行统计，计算其偏差、均方根误差和相关系数等统计量的月平均结果，再对所得的统计检验结果进行年平均得到表3。

从表3中可以发现，所有浮标的偏差均为正偏差，偏差值均小于0.15m，且偏差随预报时效变化不

大。所有浮标的均方根误差均小于0.65m，相关系数均大于0.77。其中46002、46075和41047号浮标的均方根误差随预报时效增长而增大，且相关系数随预报时效增长而减小。51003号浮标的均方根误差和相关系数不随预报时效而变化，且相关系数相比其他浮标较小。41041号浮标具有一致且较小的均方根误差，而相关系数随预报时效增长而稍有减小。32012号浮标的均方根误差随预报时效增长而减小，而相关系数基本一致。

为了进一步分析检验统计量在各浮标处的变化特征，将各统计组的月统计量结果绘制成点线图如图6所示。

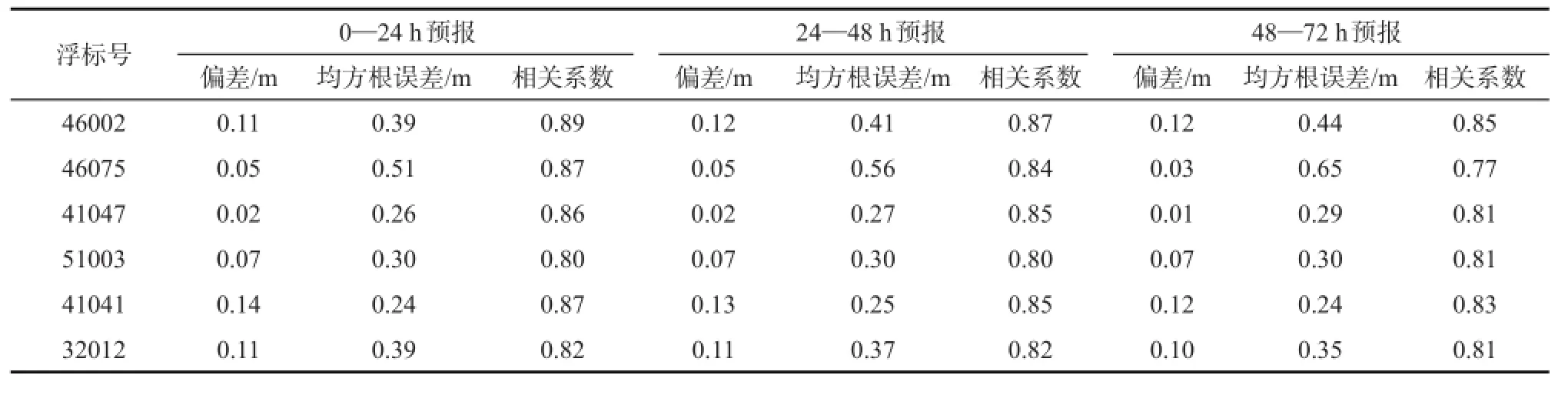
表3 浮标数据统计检验结果

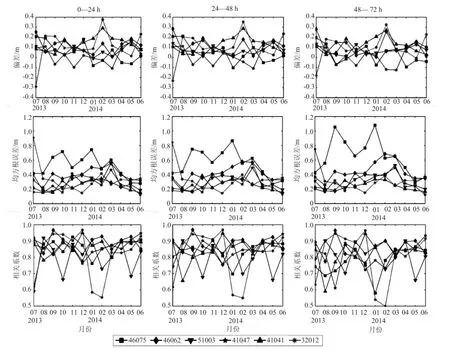
图6 浮标误差统计对比

从浮标的有效波高检验结果（见图6）中可以发现，有效波高预报误差存在着地域性差别。大多数

中低纬度浮标（除41041和32012号浮标外）的偏差绝对值均小于0.2m，且偏差随预报时效变化不大。太平洋偏差总的来说为正（除阿拉斯加水域外），北大西洋则正负偏差并存。除46075和46002号浮标外，均方根误差均在0.2—0.5m之间，且北半球浮标在3月存在明显的误差增长和极大值。46075和46002号浮标具有较大的均方根误差，尤其是46075号浮标在48 h后误差明显增大。中纬度浮标（除32012、41041和51003号浮标外）的相关系数均大于0.7，且48 h内变化不大。41041号浮标的偏差绝对值除3月外均低于0.2m，均方根误差介于0.2—0.5m之间，相关系数除8月外均大于0.75，且检验统计量随预报时效增长变化不大。32012号浮标（除7月外）的偏差和均方根误差的分布特征与41041号浮标基本一致，但相关系数在1月、2月和7月明显减小，这可能是浮标数据的问题。

5结论

本文利用国家海洋环境预报中心基于SWAN模式和NCEP预报风场模拟的全球海浪预报场，结合Jason-2卫星高度计和NDBC浮标资料对全球海浪场进行了自2013年7月到2014年6月为期1年的统计检验分析。

（1）卫星高度计和浮标验证表明，全球SWAN模式的日常预报可以较好地模拟全球海浪场。预报质量随预报时效增加而下降，预报误差在0—48 h内变化较小，而在48—72 h明显增大；

（2）卫星高度计检验结果表明，0—24 h、24—48 h和48—72 h预报的均方根误差均小于0.6m，偏差绝对值均小于0.1m，相关系数均大于0.91；

（3）卫星高度计验证结果表明，有效波高的预报偏差存在着地域性差别，全球西风带和热带地区的偏差较大，而赤道无风带和副热带高压控制地区的偏差较小。

本文中仍存在一些不足，如对预报结果仅进行了为期1年的统计检验，不利于对预报误差进行季节性变化的验证。同时没有对风场和平均波周期等海浪要素进行检验，不利于对误差形成机制得到系统的分析结果。今后将利用更长的时间序列和其他波浪要素展开更进一步的研究。

[1]Janssen PA E M,Hansen B,Bidlot JR.Verification of the ECMWFWave Forecasting System Against Buoy and Altimeter Data[J]. Weatherand Forecasting,1997,12(4):763-784.

[2]Tolman H L.Effects of Numerics on the Physics in a Third-Generation Wind-Wave Model[J].Journal of Physical Oceanography,1992,22(10):1095-1111.

[3]Tolman H L,Balasubramaniyan B,Burroughs LD,etal.Developmentand Implementation ofWind-Generated Ocean SurfaceWave ModelsatNCEP[J].Weatherand Forecasting,2002,17(2):311-333.

[4]Tolman H L.A Mosaic Approach to Wind Wave Modeling[J]. Ocean M odelling,2008,25(1-2):35-47.

[5]Chaw la A,Tolman H L,Gerald V,et al.A Multigrid Wave Forecasting Model:A New Paradigm in Operational Wave Forecasting[J].Weatherand Forecasting,2013,28(4):1057-1078.

[6]RogersW E,Wittmann PA,Wang DW C,et al.Evaluations of Global Wave Prediction at the Fleet Numerical M eteorology and Oceanography Center[J].Weather and Forecasting,2005,20(5): 745-760.

[7]Ueno K,Kohno N.The Development of the Third Generation Wave Model MRI-III for Operational Use[C]//Proc.8th Int. Workshop onWave Hindcasting and Forecasting,Hawaii,2004.

[8]许富祥.海浪预报知识讲座第十四讲海浪预报技术及预报方法(7)——海浪数值预报(Ⅲ)[J].海洋预报,2010,27(5):90-100.

[9]SWAN Team.SWAN Cycle III Version 40.51 User M anual[Z]. DelftUniversity of Technology,2600.

[10]RogersW E,Kaihatu JM,Petit H A H,et al.Diffusion Reduction in An Arbitrary Scale Third Generation Wind Wave Model [J].Ocean Engineering,2002,29(11):1357-1390.

[11]Booij N,Ris R C,Holthuijsen L H.A Third-Generation Wave Model for Coastal Regions:1.Model Description and Validation [J].Journalof GeophysicalResearch,1999,104(C4):7649-7666.

[12]Janssen PA EM.The Interaction of Ocean Waves andWind[M]. Cambridge:CambridgeUniversity Press,2004.

[13]Janssen PA E M.Progress in Ocean Wave Forecasting[J].Journal of ComputationalPhysics,2008,227(7):3572-3594.

[14]Cavaleri L,Alves JH GM,Ardhuin F,etal.WaveModelling-The State of the Art[J].Progress in Oceanography,2007,75(4):603-674.

[15]Wang Y,Jiang X W.Improvementand Application of a Saturation Based Wave Dissipation Function in SWAN Model[J].Acta Oceanologica Sinica,2012,31(1):24-32.

[16]Banner M L,Gemm rich J R,Farmer D M.Multiscale Measurements of Ocean Wave Breaking Probability[J].Journal of PhysicalOceanography,2002,32(12):3364-3375.

[17]van der Westhuysen A J,Zijlema M,Battjes J A.Nonlinear Saturation-Based Whitecapping Dissipation in SWAN for Deep

and Shallow Water[J].CoastalEngineering,2007,54(2):151-170.

[18]Hasselmann K,Barnett T P,Bouw s E,et al.M easurements of Wind-Wave Grow th and Swell Decay During the Joint North Sea Wave Project(JONSWAP)[R].Deutches Hydrographisches Institut,1973:95.

[19]Babanin A V,Soloviev Y P.Field Investigation of Transformation of theWind Wave Frequency Spectrum w ith Fetch and the Stage of Development[J].Journal of Physical Oceanography,28(4): 563-576.

[20]Ardhuin F,Chapron B,Collard F.Observation of Swell Dissipation Across Oceans[J].Geophysical Research Letters,2009,36 (6):L06607.

A p relim inary validation of globalnumerical significantwave height prediction result based on the SWANm odel

LIANG Xiao-Li1,2,WANGYi1,2
(1.NationalMarine Environment Forecasting Center,Beijing 100081China;2.Key Laboratory ofResearch on Marine Hazards Forecasting. NationalMarine Environmental Forecasting Center,Beijing 100081China)

An operationalwave forecast system was established by NationalMarine Environmental Forecasting Center(NMEFC)based on the third-generation wavemodel SWAN and globalw ind fields of NCEP from July 2013 to June 2014.A detailed study of the performance against the altimeter satellite data provided by Janson-2 satellite and buoy data from the National Data Buoy Center(NDBC)is presented.Results suggest that the forecasted significant wave heights(SWH)are in good agreement with the observed value along w ith a high correlation coefficient(＞0.91)and a low bias(＜0.1m)aswellas the RMSerror(＜0.6m)concluded in 24 h,48 h and 72 h.The accuracy of forecastwave heights decrease as the forecasting time increases,and the prediction error grows slightly w ithin 48h,but increase rapidly after 48h.Besides,the prediction errors of SWH exist regional differences.The prediction errors in the westerlies and tropical regions are bigger,while the regions of doldrumsand subtropicalhigh-pressure beltare smaller.

SWAN;wave forecast;significantwaveheight;statistical test

P731.33

A

1003-0239（2015）06-0001-09

2014-12-18

国家海洋局海洋公益性行业科研专项（201305032）

梁小力(1990-)，男，硕士在读，从事海浪预报研究。E-mail:liangxiaoli777@163.com

10.11737/j.issn.1003-0239.2015.06.001